基于李萨如图形的精确测量初相位差研究

伍泓锦，段 阳，杨浩林，樊代和,2，贾欣燕,2

(1.西南交通大学 物理科学与技术学院,四川 成都 610031;

2.物理国家级实验教学示范中心(西南交通大学)，四川 成都 611756)

众所周知，由在互相垂直方向上的2个频率成简单整数比的简谐振动所合成的规则的、稳定的闭合曲线，称为李萨如图形(Lissajous-Figure)[1]. 由于李萨如图形是2个沿着互相垂直方向的正弦(或余弦)振动的合成轨迹，因此通过对李萨如图形的分析，即可以得出2个波形的一些参数信息(如最常见的频率比等). 在通常的大学物理实验项目中，通过将2个正弦信号分别输入示波器的x通道和y通道，并将示波器设置为x-y模式，即可在示波器屏幕上显示出合成的李萨如图形. 进一步，可以通过示波器上显示的李萨如图形x方向和y方向边界的切点(或割点)个数来确定2个信号的频率比[2]，同时也可以根据图形的长宽比来判断2个信号的振幅比. 目前，有文献针对李萨如图形的性质进行了相关的研究. 例如，田芬等人通过理论推导和振幅矢量合成的方法证明了李萨如图形的重复周期性[3]. 徐定藩等人给出了李萨如图形的相同图形和高度对称图形的判定公式[4]. 黄海林等人、孙福玉等人与石涵分别都对李萨如图形的合成作图进行了计算机模拟，并简单解释了合成图与2个分振动的关系[5-7]. 而基于李萨如图形的基本性质也有相关的应用探究:例如，陈京惠等人基于李萨如图形的可叠加性提出了一种新的光纤分布传感器系统的时延估计方法[8]. 易其顺等人用其基本性质来测量音叉的频率[9]. 王红理等人利用其立体性质来测量较高频率的信号[10]. 关于李萨如图形的其他一些性质研究也在文献[11]中进行了简单的总结. 然而，以上所有已报道的成果均为研究由已知正弦函数参数后所合成出的李萨如图形的性质，均属正向分析过程. 到目前为止，仅郑俊达进行了由李萨如图形来逆向分析正弦函数相关性质的研究[12]，但其也仅仅提供了一种分析2个同频信号(频率比为1∶1)之间相位差的方法. 而实际中绝大多数情况则是合成李萨如图形的2个信号的频率是不相同的. 因此，如何通过已知某一合成李萨如图形，来反向获取2个正弦信号的参数，特别是2个正弦信号的初相位差信息的研究，到目前为止还未见报道. 基于此，本文详细研究了利用已合成出的李萨如图形的规律和性质，给出用来合成李萨如图形的2个任意未知正弦函数初相位差的方法，因此该方法可最大程度地获取2个正弦函数参数的信息.

1 理论分析

考虑一个由x方向和y方向分别如式(1)所示的正弦函数合成的李萨如图形. 假设其x方向正弦函数的初相位为0，则y方向正弦函数的初相位φ即为2者的初相位差.

(1)

式(1)中，t表示时间，x和y函数的振幅分别为A和B，频率分别为p和q. 特别地，当选择参数A=2，B=1，p=2，q=3，φ=π/12时，合成的李萨如图形可如图1所示,其中M表示图形x方向上的长度，N表示图形y方向上的长度，C表示图形上最靠右上方的点，a表示C点与图形右方边界的距离.

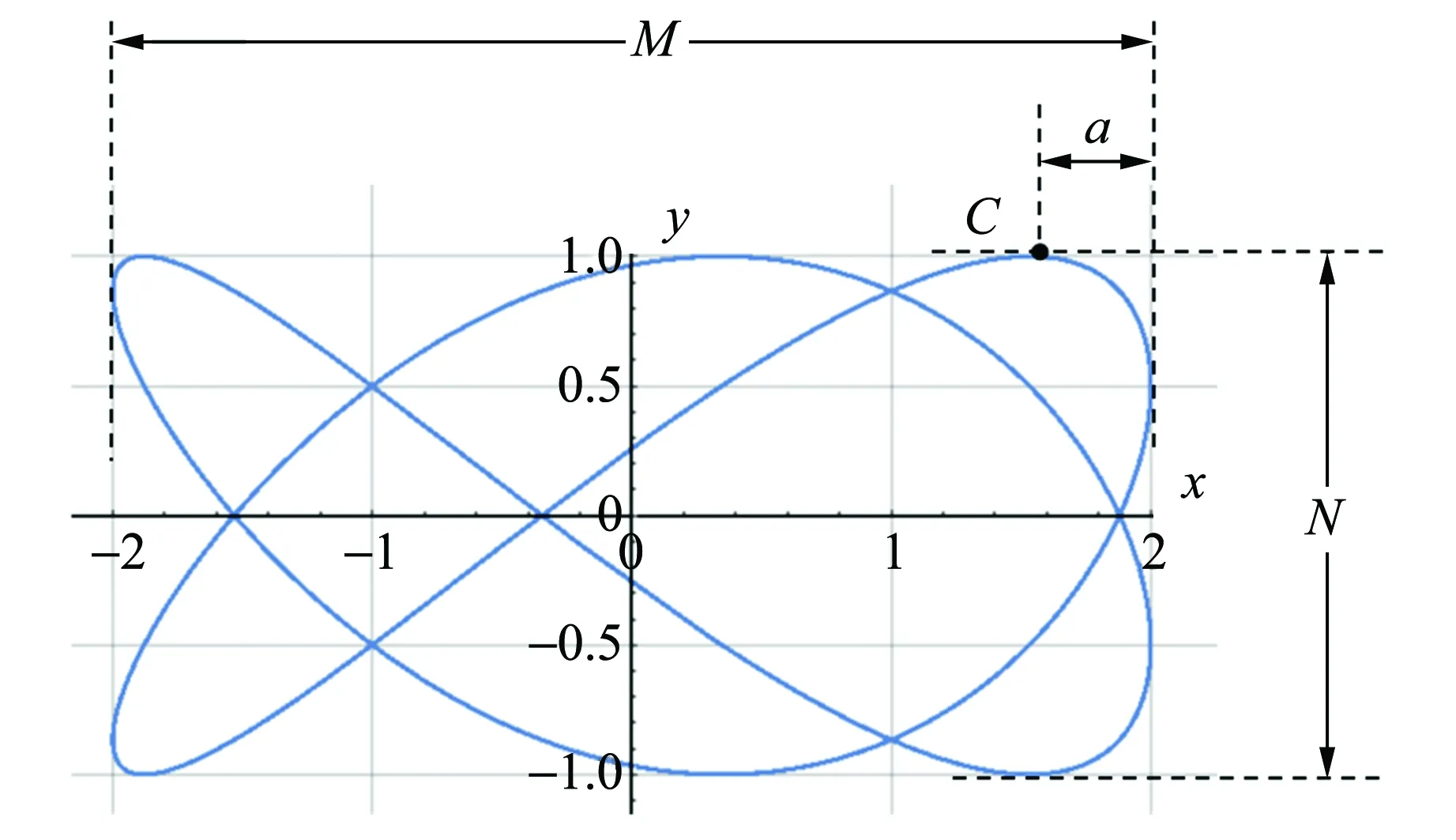
图1 合成的李萨如图形

假设测量出李萨如图形x方向和y方向的长度分别为M和N，则可以得出

(2)

传统的大学物理实验内容，均是已知李萨如图形以及x方向的正弦函数频率p值，来获取y方向正弦函数的频率q的值. 例如，对图1所示的李萨如图形，可以得知水平方向的切点数nx=3以及垂直方向的切点数ny=2，最后利用

(3)

以及x方向函数的频率p=2，得到y方向函数的频率q=pnx/ny=3.

与传统大学物理实验内容不同的是，本文将重点分析在已知李萨如图形形状以及如式(1)所示的x方向函数的频率p值情况下，如何获取y方向和x方向正弦信号的相位差信息φ，特别是在p∶q≠1的情况时.

将式(1)中的时间参量t约去，化成y关于x的函数可得：

(4)

事实上式(4)描述的即为在xy平面上的李萨如图形. 为了方便求解式(4)中φ的值，可以在李萨如图形上选取一条特定的、平行于x轴的直线，例如，选取y=B=N/2这条直线. 该直线将与李萨如图形有若干切点(xi,N/2)(i=1,2,3，…). 此时，式(4)就可以化简为：

(5)

通过式(5)，可以进一步得到：

(6)

其中，kl=0,±1,±2,….

当李萨如图形确定时，参数M,nx,ny为确定值. 此时，从式(6)可以看出，xi的值将只取决于kl和φ的值. 可以将xi的最大值xmax(即李萨如图形与y=N/2所表示的直线相切的最大值点坐标，如图1中C点所示)带入式(6)，来获取φ的信息. 此时，式(6)即可进一步改写为：

(7)

针对具体的李萨如图形，不妨设点(xmax,N/2)到图形右边界的距离为a(如图1所示)，此时，根据几何关系xmax=M/2-a，可将式(7)最终写为：

(8)

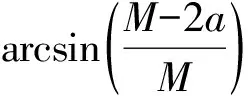
2 实验验证

示波器上显示如图2所示的李萨如图形，根据上述提出的方法来获取y方向上正弦函数的初相位值，此值也为x方向上和y方向上信号的相位差值.

图2 实验产生的李萨如图形

首先，根据示波器面板上的格数尺，可以测量出李萨如图形x方向和y方向的长度，分别为M=9.6 div和N=6.4 div. 然后，可从图2进一步得知，水平方向和垂直方向的切点数分别为nx=3和ny=2. 最后，也可以测量出图2中a的长度为1.7 div. 将上述测量结果代入式(8)，最终即可得出y方向函数的初相位值φ为

(9)

考虑到式(9)中arcsin函数的多值性，进一步求解式(9)，可以得出φ的可能值为

(10)

(11)

其中，k2=0,±1,±2,…,分别将k1和k2的可能取值代入式(10)～(11)，最终可以得出如表1和表2所示的φ的取值(-π≤φ≤π).

当k1和k2取其他整数时，得出的φ的值要么与表中得出的结果一致，要么超出了±π的范围，因此不在表中列出.

从表1和表2可以看出，对于如图2所示的实际李萨如图形，在已知x方向函数参数的情况下，同一个李萨如图形实际上可能对着若干个不同的初相位φ值.

表1 利用(10)式得出的φ的可能值

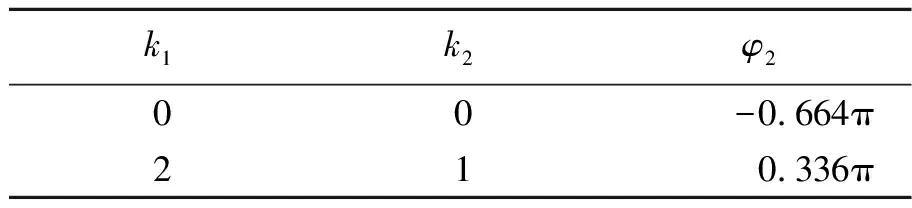
表2 利用(11)式得出的φ的可能值

实际上，图2所示的李萨如图形，是利用双通道信号发生器，通过设置如图3所示的参量来生成的. 其中CH1通道信号的参量设置为fx=2 kHz，Ax=2.4 V，φx=0，然后将其连接到示波器的x通道. CH2通道信号的参量设置为fy=3 kHz，Ay=1.6 V，φy=π/6≈0.167π，将其连接到示波器的y通道，最终合成了李萨如图形. 此时，φy的值即为所要得出的初相位差值φ.

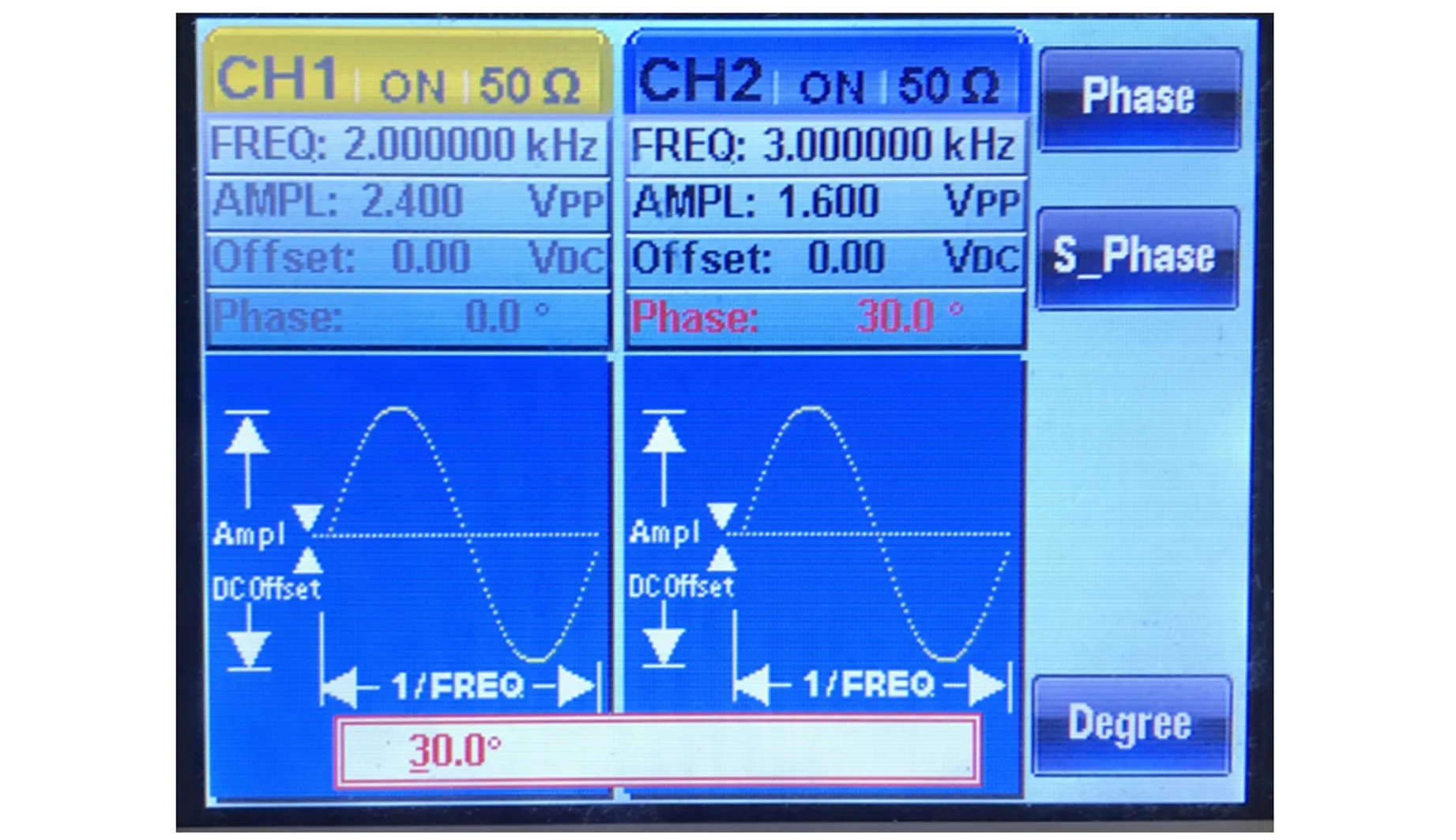
图3 信号发生器参数设置图

从表1得出的结果可以看出，利用本文提出的分析方法得出的结果之一(0.164π)，与设置值(π/6)相比，相对误差约为1.8%，证明了本文提出方法的适用性.

值得注意的是，从表1和表2的结果可看出，如图2所示的李萨如图形，也可以得出初相位差φ(-π≤φ≤π)的其他可能取值有：-0.836π，-0.664π，0.336π. 因此，在不改变信号发生器的其他参量下，仅改变CH2通道的相位值φy，在示波器上显示了合成的李萨如图形，如图4所示.

从图4实际合成的李萨如图形可以看出，当初相位差分别为表1和表2所示的值时，将得出完全相同的李萨如图形.

(a)φy=-0.836π

(b)φy=-0.664π

(c)φy=0.336π图4 仅改变φy值时，合成的李萨如图形

3 结束语

从李萨如图形的结构和特点出发，提出了通过李萨如图形来获取合成图形的2个互相垂直方向正弦信号的初相位差的方法. 当已知水平方向(如x方向)正弦函数的参量时，通过合成的李萨如图形，提出一种获得垂直方向(如y方向)正弦函数的相位信息的方法，进而获取2个垂直方向信号的初相位差信息. 通过研究发现，对于特定的李萨如图形，2个互相垂直的信号的初相位差并不唯一，存在多种可能值. 最后对理论分析结果进行验证，实验结果与理论分析基本一致.