真实步伐荷载作用下人行桥振动及共振加速分析

2019-12-27李泽民吴冬雁刘宣含赵俊亮

噪声与振动控制 2019年6期

李泽民，吴冬雁，刘宣含，赵俊亮

（温州大学建筑工程学院，浙江温州325000）

近年随着伦敦千禧桥、法国Solférino桥[1]等一系列人行桥振动问题的出现，人行振动荷载作用下人行桥的振动问题得到了广泛的关注，其中人行振动荷载的准确模拟成为解决人行桥振动问题的关键。

对于人行桥人致振动计算发展出了多种行人模型，如移动质量、单自由度质量-弹簧-阻尼系统、双足模型[2-3]等，但由于上述人-桥耦合模型计算复杂且部分行人参数难以确定导致应用受限，而基于傅里叶展开得到的简谐步伐力因为力学模型简单而得到了广泛的研究与应用。Ricciardelli 等[4]采用解析方法得到了简支梁桥在共振及非共振正弦移动荷载作用下竖向峰值加速度的计算公式；C.C.Caprani[5]采用随机移动简谐作用模拟行人荷载并基于蒙特卡洛框架提出了全局模态精细积分计算方法；陈舟[6]等基于单人移动荷载模型推导了竖向振动计算解析表达式，并以此给出了简化振动频率响应函数以计算振动响应的峰值加速度。而基于1阶移动简谐力简化计算，多个国家人行桥规范，如BS 5400[7]、HIVOSS[8]、Setra[9]等给出了简支或连续人行桥在单人作用下共振峰值加速度的计算公式以用于结构振动舒适性评价。

虽然以移动简谐力为代表的人致振动计算得到了广泛的研究，但研究大多集中于1 阶简谐力作用下的简化分析，而忽略了高阶部分的影响，导致简化单人荷载模型与真实步伐力有一定差距，引起人致振动响应计算出现偏差。本文以单人行走左、右脚空间交替前行产生的实测竖向脚步步伐力为人行振动荷载，真实模拟行人行走过程中其对结构的竖向作用，进行人致振动响应的精确估算，并通过一实际人行桥人致振动试验验证了该法的准确性；再以共振步伐荷载下的结构竖向加速度峰值为目标，与各国规范、文献的计算结果进行对比，可为人行桥振动舒适性评价及设计提供参考。

1 真实步伐荷载模拟及振动计算方法

1.1 真实步伐荷载模拟

人在行走过程中对结构的作用表现为左、右脚掌交替以步宽W、步长l与地面接触时产生的空间步伐力，如图1所示。为了真实模拟步伐荷载作用，本文同时考虑两脚步宽及左、右脚前后交替步长产生的空间效应。

图1 行走双脚步伐力作用示意图

图2 单脚地面竖向步伐力实测

其中，每步步伐力大小通过实测行走步伐力得到，如图2所示为瑞士规范中根据步伐力实验结果[10]提供的常速行走（步频范围1.5 Hz～2.3 Hz）时不同步频的竖向步伐力模型，以步伐力动力系数αv计，每步竖向步伐力可由式（1）得到

式中：G为行人体重，fp为行走步频。

1.2 人致振动响应计算方法

为了精确计算结构在单人行走步伐力作用下的振动响应，采用左、右脚空间交替前行的真实步伐力来模拟行人振动荷载，行人以步宽W、步长l及步频fp沿人行桥中心线行进时，得到结构人致振动方程如式(2)所示

式中：M、K和C分别为桥梁结构的质量矩阵、刚度矩阵以及阻尼矩阵，、、u分别为结构加速度、速度和位移响应；Fr和Fl分别为单人左、右脚产生的步伐荷载力，δ(x)为Dirac函数，每个步伐力作用于脚掌与地面接触的位置，以步长l交替向前；fl与fr分别为左、右脚真实步伐荷载，由式（1）得到。

结构阻尼采用经典Rayleigh 阻尼近似，根据结构振动特性试验测得或采用规范推荐值。振动响应求解即为每个时间步中步伐荷载下的振动响应计算，数值计算采用Newmark-β法，β值取为0.25。

2 实例应用分析

2.1 实测桥梁概况及结构振动试验

为了验证本文计算方法的适用性，以一座钢桁架简支人行天桥为试验对象，进行振动特性及人行振动荷载下结构振动试验，与本文计算结果进行对比分析。

如图3所示为一钢桁架人行天桥，主桥采用单跨为42.06 m、桥面总宽为4.7 m 的钢桁架结构。人行天桥由两片钢桁架通过上下横梁连接而成，每片钢桁架高为4.6 m，由上、下弦杆、腹杆、竖杆组成。桥面人行道板净宽为4.4 m，桥面板由3 cm花岗岩铺装+3 cm水泥砂浆+13 cm混凝土+压型钢板组成，楼梯钢筋混凝土板式结构与主跨结构分离。

为了得到结构的自振特性及人行振动荷载下结构竖向振动响应特性，对人行桥进行了动载试验。试验中采用高灵敏度低频加速度传感器及配套设备，传感器测点布置如图3（c）所示，采样频率设为256 Hz，测试中对结构振动竖向加速度时程进行记录分析。

2.2 结构振动模态参数识别

图3 桥型布置及测点布置图（单位：cm）

采用脉动法及跳击法分别对结构自振频率及振动阻尼比进行识别。由于真实结构受到外界环境影响，为了剔除噪声对结果的影响，采用快速傅里叶变换（FFT）与特征系统算法（ERA）相结合的方法，具体如下：

(1)对结构多组脉动或跳击自由衰减振动响应进行FFT 分析，提取多组数据中都稳定出现的频率结果；

(2)采用ERA 法对多组自由衰减振动响应进行模态分析，得到不同阶数N下的结构模态参数（包括自振频率、振动阻尼比，模态置信因子，模态相位角及模态振幅），提取模态置信因子大于0.99且各模态参数稳定的结果；

(3)对比ERA 法与FFT 法，提取ERA 法中自振频率与FFT 法相一致的模态参数作为最终识别结果。

如图4所示为跨中结构脉动及自由衰减振动一例与对应的FFT分析和ERA分析结果。

由图4可得：

(1)结合脉动响应下FFT 频谱结果与ERA 频率稳定图及模态参数，得到结构第1 阶竖向对称、2 阶竖向反对称振型的自振频率分别为4.09 Hz 和18.0 Hz；

(2)采用ERA 法对多组跳击工况下自由衰减振动分析，发现识别到的不同组振动阻尼比存在一定的浮动（第1、2 阶振动阻尼比变化范围分别为0.32%～0.52%和0.69%～0.82%），取不同组中出现频率较高值作为识别结果，得到第1、2 阶振型（f=4.09 Hz、18.0 Hz）对应的振动阻尼比分别为0.38 %和0.7%，拟合得到结构Rayleigh阻尼C=a0M+a1K，a0和a1分别为0.112 39和0.000 13，如图4(c)曲线所示。

2.3 人行真实步伐荷载振动试验对比分析

为了验证计算方法的准确性，对单人行走作用下的振动响应计算值与试验进行对比分析。

为了减少环境噪声对振动响应的影响，采用多人齐步走作用下的振动响应除以人数获得单人振动荷载下响应。如图5所示为单人行走过桥作用下，实测得到的跨中位置A1 的加速度时程响应及对应的FFT分析、小波分析结果。

由图5可得：

(1)根据小波对频谱-时程分析可得结构1 阶振动在整个时间段都起主导作用，而行走步频2.3 Hz的荷载频率在行人经过跨中附近时比较卓越；

(2)在行人经过桥跨测点附近时，激发高阶局部桥面板振动振型，并随行人离开而迅速衰减；

(3)为了提取行人振动荷载作用下的结构振动加速度峰值，对时程响应进行高频滤波处理，如图所示实线为滤波8 Hz以上高频后得到的时程对比图，得到加速度峰值为0.008 89 m/s2。

图4 实测时程响应及振动特性分析

图5 行人行走时程响应分析

根据上述行人行走的特点及结构振动参数，采用本文提出的计算方法建立简支人行桥模型进行计算，其中结构振动阻尼比采用上述识别方法得到系数，体重取3 人平均体重68 kg、过桥时行走步频为2.3 Hz、步长0.67 m、步宽0.15 m。如图6所示。

图6 计算与实测振动时程响应对比

将计算得到的跨中处加速度时程与实测的时程对比，计算得到的加速度峰值为0.008 47 m/s2，与实测结果较相符（误差率4.7%），表明本文提出的真实步伐荷载下的人致振动计算方法具有较高的精度。

3 共振峰值加速度对比分析

3.1 规范、文献共振峰值加速度计算方法

各国规范对于人行桥竖向振动的规定主要为了避开对结构行走敏感频率区域和对共振步伐荷载下结构峰值加速度响应的限制。

为了避免结构基频落于人正常行走的步频范围（1.6 Hz～2.4 Hz）而引起结构共振（即结构基频f1=步频fp），如中国人行天桥规范[11]要求结构基频大于3 Hz，但对于基频大于3 Hz 的人行桥仍存在出现2 阶超谐共振问题（即f1=2fp），因此，需要对2阶超谐共振下的加速度峰值进行计算评估。多个规范、文献中单人共振（超谐共振）下简支人行桥跨中竖向加速度峰值的计算公式如式(3)至式(9)及图7所示。

式中f1为结构基频，Hz；L为简支梁跨径，m；m1为模态质量，m1=mL/2，m为单位长度质量kg/m；M为全桥质量M=mL；ξ1为结构1 阶阻尼比；ψ(f1)为结构基频偏离步频时衰减系数，如图7(a)所示；ys为结构在跨中集中力作用下静态位移，简支梁在跨中700N作用下的变形，ys=700N∙L3/48EI，E和I分别为结构弹性模量和截面惯性矩；ψ为结构振动动力系数，BS 5400和FIB 1阶共振步频如图7(b)所示，图中横坐标分别为跨径L和n=L/l，l为单步步长，2阶共振步频取图中数值的0.25倍；ε为计算参数ε=n∙ξ1；α为步伐力傅里叶展开比例系数，1、2阶共振步频分别取为0.4和0.1；G为行人体重，取为700 N。

图7 计算参数图式

3.2 峰值加速度对比分析

为了比较本文提出的计算方法与规范、文献计算值的差异，比较前述结构在2 阶超谐共振下跨中峰值加速度，如图8所示。

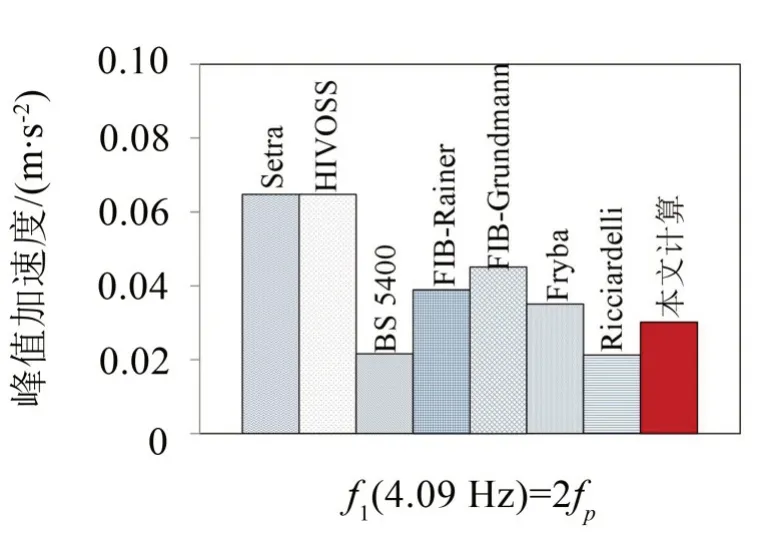
图8 峰值加速度比较图

由图8可得：

(1)由于各国规范对步伐荷载的简化方法不同，故计算结果亦不相同，Setra 与HIVOSS 规范采用稳定正弦分布力模拟人行荷载，而BS5400、FIB、Ricciardelli、Fryba 采用1 阶移动正弦集中力，本文则采用完全真实步伐力进行模拟；

(2)基于Setra与HIVOSS的计算结果偏大，而基于BS5400 的结果与Fryba 相同，由于基于最大峰值发生在行人经过跨中位置时这一错误假设造成结果偏小，FIB 与Ricciardelli 结果较本文偏大；在上述1阶正弦移动力作用下，基于Ricciardelli 的计算精度最高，与本文计算结果亦最接近，但仍有一定差异，表明不考虑高阶步频成分对结构振动会产生一定影响。