基于非负Tucker3分解理论的车内主动降噪控制研究及应用

2019-12-27赵红飞王海军

噪声与振动控制 2019年6期

赵红飞，王海军，韦宁

（上汽通用五菱汽车股份有限公司，广西柳州545007）

车内声品质与车内低频噪声的声压级（SPL）有比较密切的关系[1]，采用主动降噪控制（Active Noise Control，ANC）处理怠速车内噪声可使降噪量超过10 dB(A)，对声品质的改善较被动控制具有明显优势[2]。但是，车辆在不同工况下行驶时车内噪声传播具有非线性、随机性和非稳态强的特点，给传统单通道前馈式ANC系统带来难以确定目标函数的问题，导致次级通道的噪声反馈失效。对此，Gonzalez 等提出了一种多通道前馈式ANC 调节车内声品质的响度和尖锐度的方法，结果表明对低频噪声效果明显，车内SPL的降低与噪声受ANC控制时的衰减水平有关，但受非稳定噪声信号影响，容易出现客观评价与主观评价不一致的问题[3]。为改善次级通道的反馈能力，国内外学者集成了对ANC系统采用加权最小均方误差准则和优化次级通道信噪比的方法，通过对次级通道的频谱特征进行自适应滤波优化与加权监控，降低了计算要求和信号泄漏量，提高了次级通道信噪比水平，试验效果较好，但是算法对加权阀值的选择具有较强的依赖性，以及要求具有准确性较高的路谱条件[4-8]。因此，并行式多通道ANC处理解决问题的关键是以次级通道的最小误差控制与反馈能提高LMS（Least mean square algrithm）算法的效率和自适应性[9-11]。这些研究均表明要降低人耳感知的声压级和时滞性，关键在于增强ANC目标函数的选取，以提高次级通道的反馈能力和系统的降噪性能，进而提高车内声品质。

本文结合自适应FIR(Finite Impulse Response)滤波器，综合考虑输入端-反馈端的计算难度和误差性两方面来提高ANC的性能。根据非负Tucker3分解(Nonnegative Tucker3 Decomposition, NTD)理论滤掉局部特征信号和高频噪声的干扰，从而解决多样本、非线性和非稳定随机信号的干扰问题[12]。另外，结合自适应FIR滤波处理进行频域范围反馈，不但可以提高计算速率，与次级通道的反馈形成闭环控制，还将改善系统的自适应性和鲁棒性。因此，研究与开发ANC 系统，不仅在理论上显得必要，对在主机厂进行的主动降噪实践也具有重要意义。

1 非负Tucker3 算法理论与子特征集成

NTD算法是非负矩阵分解(NMF)和非负张量分解(NTF)的一种广义形式，也可称为高阶支持向量机(SVM)，能够提取出具有比较稀疏特性的局部信号。根据文献[13]，三维数组的NTD 算法的物理模型如图1所示。

完成噪声采集后，提取不同时域噪声信号双谱特征{S1,S2,…,Sn}，进行二维矩阵转化，再映射成三维化后，便可得到三维张量Y。例如，图2所示是一个3阶噪声信号转化过程。

根据噪声信号在不同时域中的表现，则Y整体上可抽象成由不同的子噪声张量y缩并组成，即

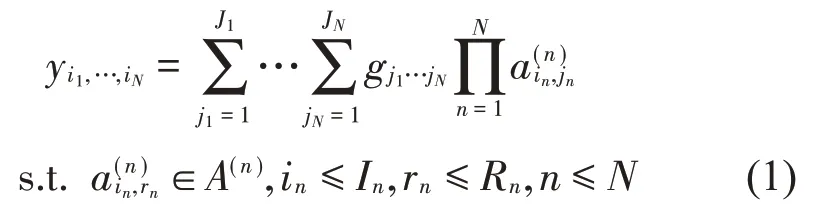
式中：a表示子噪声特征向量，g为子特征值，N为噪声特征的总个数，n为子噪声所在的某一位置。为了便于书写，式（1）常写为张量和矩阵的形式，即

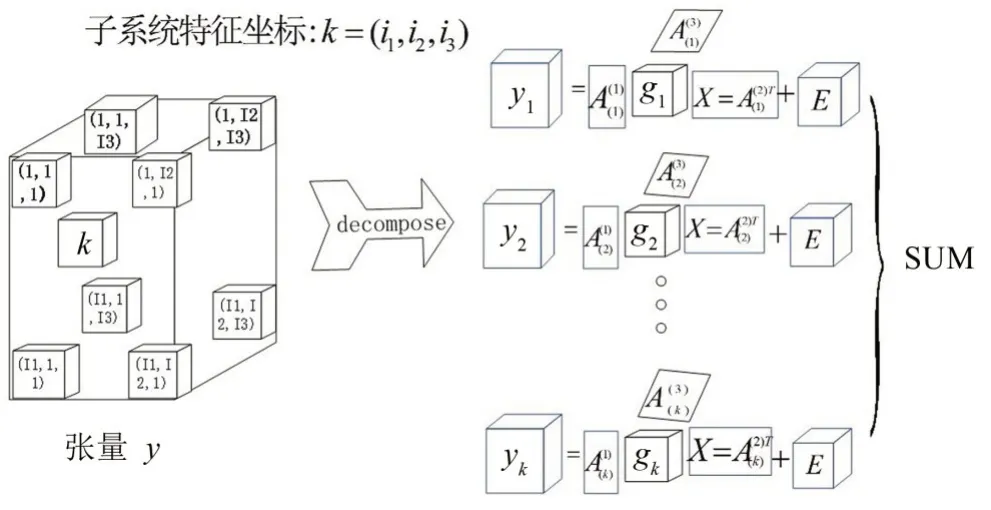
图1 NTD的三维特征提取模型

图2 3阶噪声信号转化张量过程

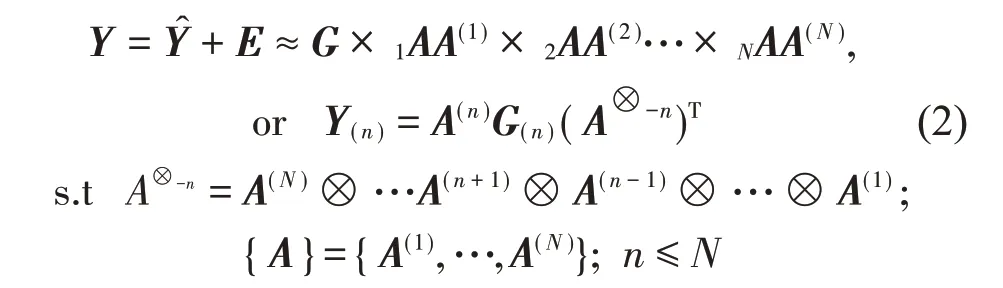
式中：E表示计算误差，A⊗-n表示所有的除了模矩阵A(n)外所有模矩阵的Kronecker积。Yˆ是Y的近似值。Y(n)是张量Y沿n方向上的展开矩阵(展开方式参考文献[14])。传统型ANC 在处理过程中遇到的迟滞问题产生的原因大多是因为工况复杂，数据量大，造成目标函数的选取以及数据处理困难，导致ANC系统次级通道反馈滞后使得降噪失效。而NTD 能快速完成数据分解，产生稀疏性良好的局部信号特征，适合自适应滤波，从理论上讲，有利于降低数据的复杂性和提高系统的可靠性。

2 ANC模型及其优化

2.1 传统ANC模型

ANC的基本思想是当噪声以即时信号传递时，系统会对初级通道的噪声进行实时监控，采用系统算法对噪声进行相位解析后，由车内扬声器释放出与噪声相反的声波，以此有效抵消噪音幅值，降低车内噪声，全面净化成员的听觉环境，提高车内声品质[8]，原理模型如图3所示。

当输入端通道为线性不变信号x(n)时，经过FIR滤波器后信号为

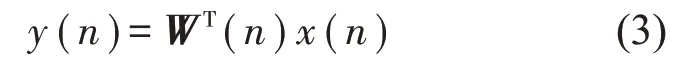
若次级通道中的信号发生器产生的信号为d(n)，不考虑相位误差时，振幅误差为

图3 主动降噪的基本原理

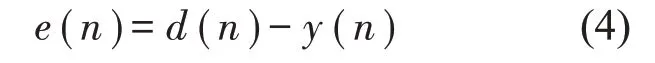
若系统中存在闭环控制，将以上误差作为加权基础，以LMS（Least Mean Square）型前馈式算法进行误差补偿

其中W(n)为FIR的权值，α为一常量值。将ANC系统进行模块化设计，不仅可以改善声品质，同时可提高系统内部的独立性、互换性和通用性，还简化了系统整体结构。

2.2 非负约束型ANC系统及其控制

针对迟滞现象，采用带通滤波器采集特定频率信号进行相位补偿，建立相位差计算模块获得信号之间相位差，构造移相器控制目标信号，以补偿传输过程中信号产生的相位延迟，解决系统的迟滞问题。同时，结合NTD 和ANC 进行NCANC(Nonnegative Constraint ANC，简称NCANC)降噪滤波，确保各通道间不干涉，从而提高算法的健壮性和控制系统的鲁棒性，该系统的模型原理如图4所示。

图4 NCANC控制系统（时域）

图4中，NR、NC、N'C、NE、N'C和N'F均为麦克风（声传感器），w1,n为输入通道的自适应滤波器，Sm,m(m≤M)和(m≤M)分别为子系统的初级通道特征信号以及次级通道发出的补偿信号，eM[n]和e'MM[n]分别为输出通道和反馈通道的误差值，即

其中S(m,j)是次级转换通道与第m个麦克风间的特征信号，w(n+1,j)是L阶FIR滤波器，x[n]为发生器信号。因此，对于误差补偿反馈通道，误差可写为

当式（6）中的信号在时域内计算时，因为峰值点比较多，计算量大，对系统性能要求高，且易使次级反馈通道和LMS 计算（FIR 滤波器设置见文献[7,10]）发生过拟合效应，所以，考虑在频域内进行有针对性的降噪，在理论上可以降低计算复杂性，对解决时滞也将起到关键性作用，改善后的NCANC 控制系统模型如图5所示。

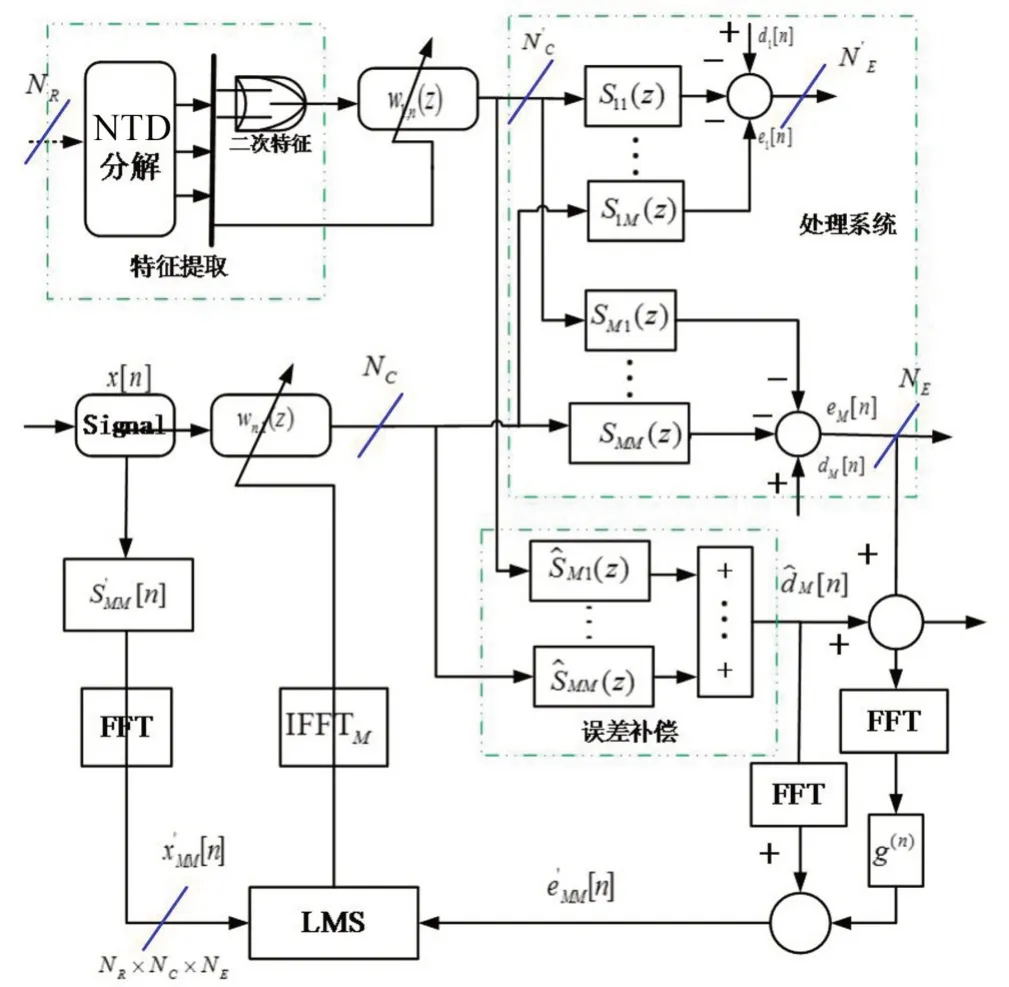
图5 频域内的NCANC系统

相比于时域内的NCANC控制系统，在图5中控制器和误差补偿通道输出端完成了FFT 变化，使信号在频域内进行比较，一方面有利于LMS的输入端能有效进行频谱噪声比较，减少全时频段降噪信号识别的必要性；另一方面在频域范围内有效的补偿也使得比较误差e′MM[n]降低，可达到提高算法效率的目的。由于噪声采样率约为20 kSPS，需要在一个采样周期（50 μs）内完成一次2 阶控制算法的计算，加上对多通道实时控制的要求，即50 μs内要进行至少两次2阶控制计算，因此NCANC系统的控制流程如图6所示。

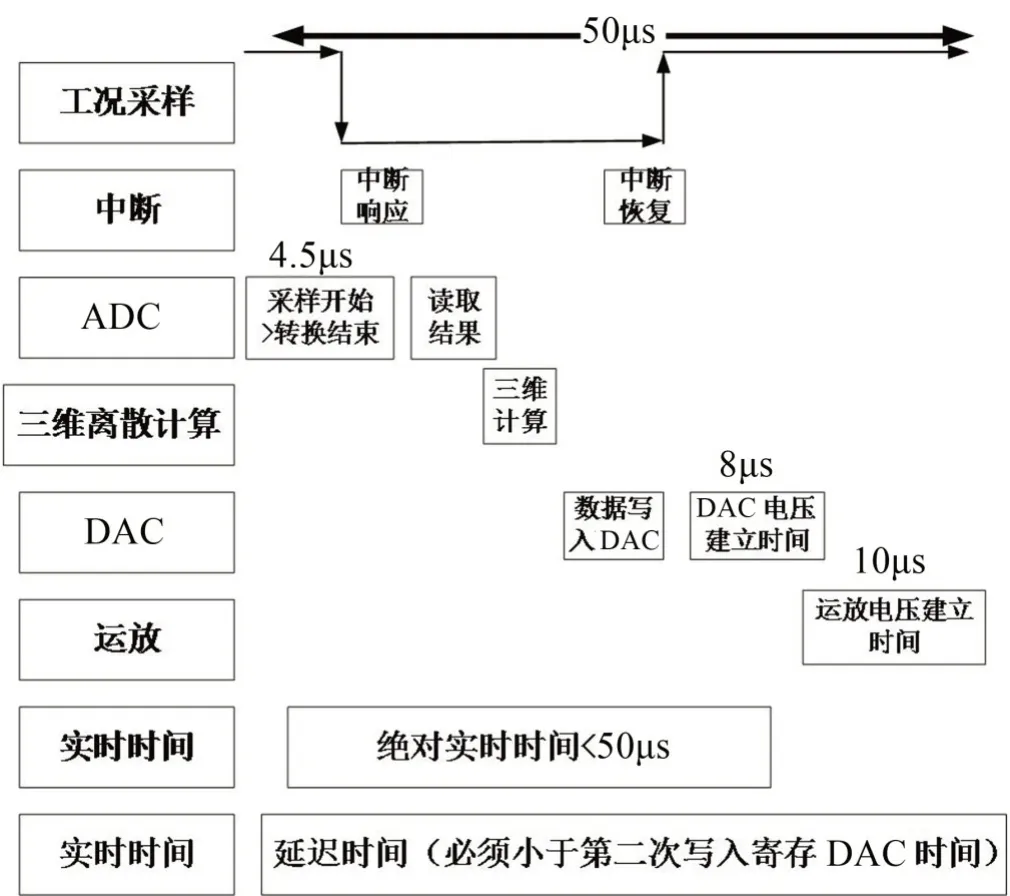
图6 NCANC系统的实施与控制图

图6主要包括工况采样、时钟中断、模式转换控制（ADC）、三维离散计算（张量分解、向量计算）、数模转换控制（DAC）、运放、实时时间控制等几个策略组成部分，可通过嵌入式单片机集成电路实现。本文选择以色列Silentium 公司开发的S-CubeTMANC系统，其具有256 kb/s的处理能力，理论上具有降低1 000 Hz以内噪声的能力。

3 NCANC系统验证及其应用研究

3.1 随机信号仿真验证

随机信号主要包括平稳信号和非平稳信号，在实际工况中，对于汽车车内噪声信号发生器不仅要满足平稳工况下的降噪要求，更要避免非平稳工况下的计算误差和时滞现象。现在分别采用一组2阶次信号和一组3阶次信号作为验证对象，其中2阶次信号是由频率为π 3 和π 4 的正弦信号叠加组成，随机信号由高斯随机数组成，长度均为1 000个采样点。为了评价计算误差，计算精度采用均方差根，即

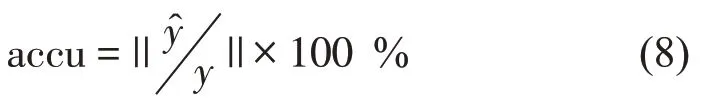
经过NCANC 系统计算后，信号产生器发出的拟合信号主要包括平稳工况下的2、4 和6 次拟合信号，对非平稳信号主要包括3、5 和7 次拟合信号，拟合效果如图7所示（计算精度和时间见表1）。

由表1和图7中所知，NCANC 对平稳信号和平稳信号的拟合精度都达到了96%以上，计算时间在3微秒以内，而人体能感知的时滞误差为0.01秒。增加该约束器后，该系统性能上能满足要求。其实，算法对降噪过程中的稀疏性（单位体积内含有特征值的个数）也有了较大的改善，如表2所示。

表1 NCANC处理平稳和非平稳信号的计算精度和时间（精度：accu/%；时间：10-3 t/s）

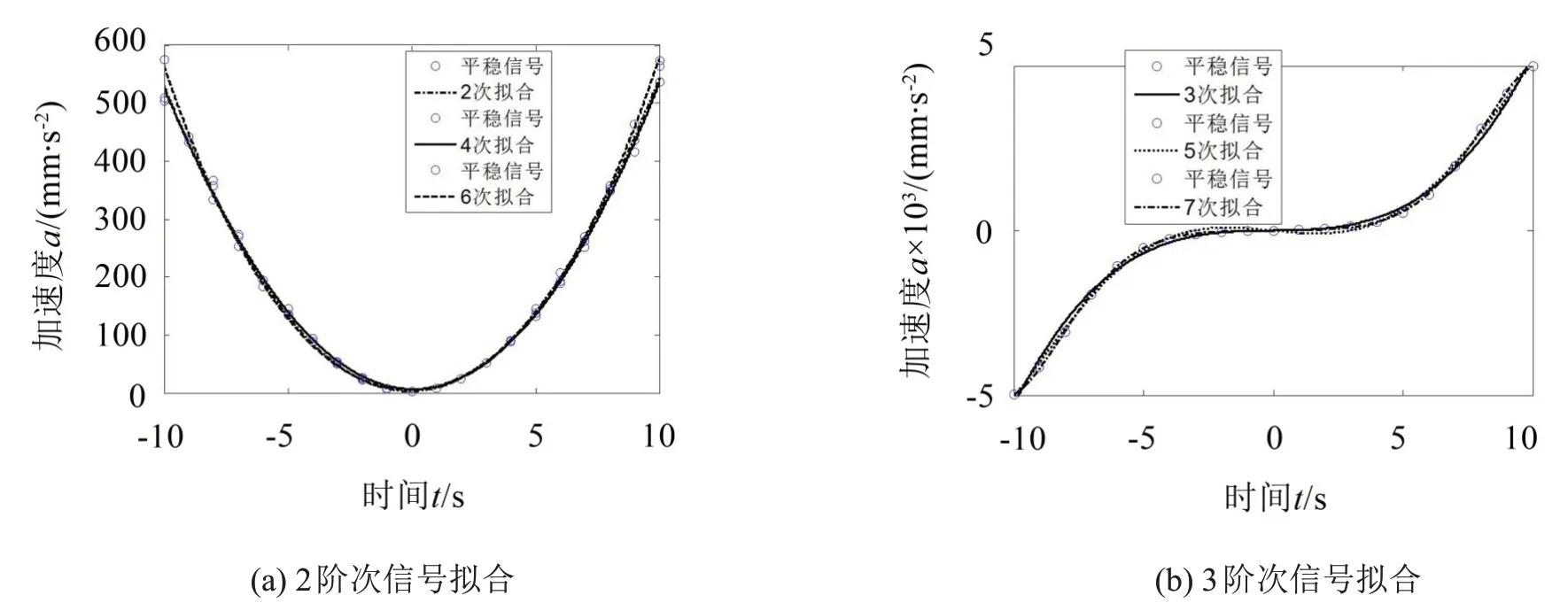
图7 NCANC系统仿真信号拟合

表2 子系统张量核切片中特征值个数/个

增加非负约束后，张量核中的特征值个数由77个降低至12 个，从并行计算复杂度上讲，相当于降低了84.4%的计算内存，提高了ACANC，有利于改善效率。

3.2 降噪应用

以某MPV车型为研究对象，对该车进行采样布点如图8所示。

本次研究需要使用16个传感器，相对应参考点如表3所示（为便于分析，括号里面的数字表示传感器的参考位置点序号）。完成布置和设定工况后，可进行数据采样。

图8 采样传感器安装点

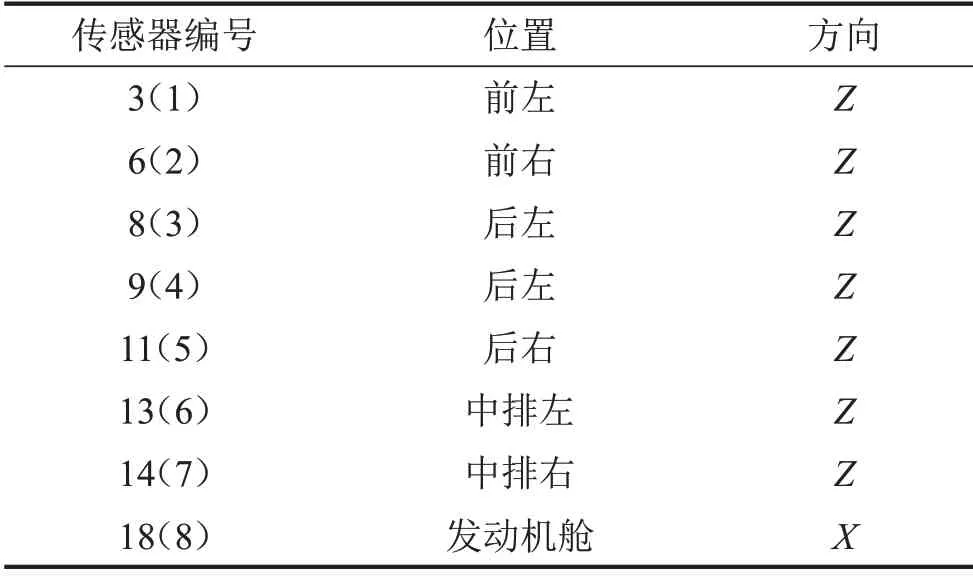
表3 传感器编号与采样参考点

分别在3 000 rmp、4 档60 kph 至70 kph 和4 档80 kph（3000 r/min）时速工况下进行匹配标定和数据采集，匹配时需要调节标定设备和软件达到稳定值再读取其误差值，分别进行2次，得到的相关性分析见表4。相关性误差指标是特定路面在某工况下的噪声值与测试值之间的误差值；仿真值误差是由ACANC次级通道发出的噪声与测试值之间的误差。令驾驶员位置处的相关性误差和仿真值误差分别为Errc和Errs，则分别为

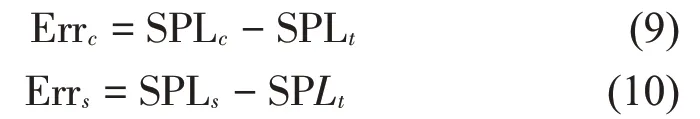
其中：SPLc、SPLt和SPLs分别表示标定声压级、实际测试声压级和仿真得到的声压级。

表4说明路噪和发动机噪声的相关性和仿真值从趋势上基本保持一致，最大误差仅为3.1 dB左右，3种工况下的分析数据接近实测值；该车噪声主要包括路噪和发动机噪声，其中3、6、8、9 和11 传感器测得信号主要为路噪，13、14 和18 传感器测得信号主要为发动机噪声，如图9所示（图9中横坐标数字含义同表3括号中数字，表示传感器的参考位置点序号）。

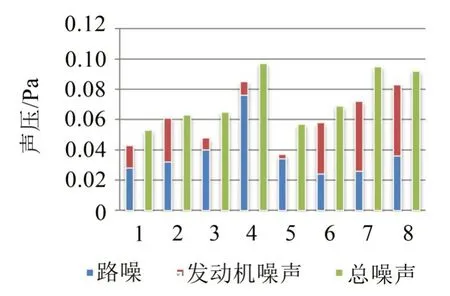
图9 每个麦克风测得的噪声及主要贡献源

很明显，图9中路噪和发动机噪声这2类噪声经初步统计占了麦克风总体噪声85%以上，且路噪和发动机噪声相对独立，为采用NCANC 做降噪处理提供了良好条件。在驾驶员位置的降噪效果经过标定后如图10所示。

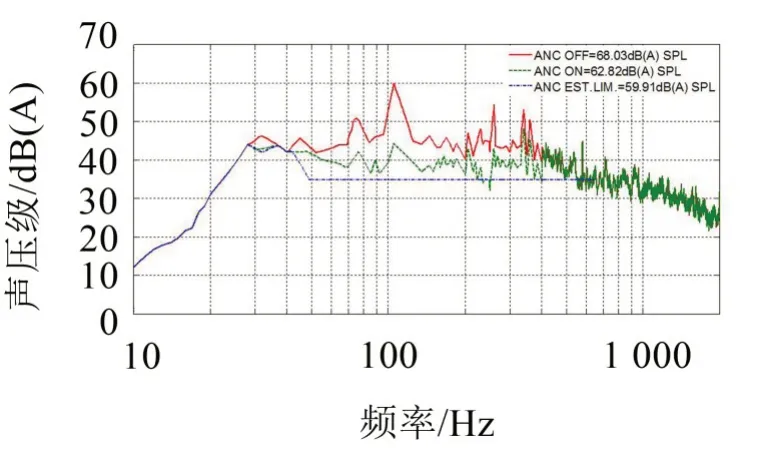
图10 NCANC系统降噪效果

如图10所示，开启NCANC后，500 Hz以内噪声明显降低，驾驶员位置处的总声压级从68.03 dB(A)降到62.82 dB(A)，即整车总声压级降低5.21 dB(A)。在76 Hz 和105 Hz 处取得了较明显的降噪效果，其中在105 Hz 处降低最高约15 dB(A)。从频域上看，系统没有出现时滞现象，从而提高了车内声品质。