全柔性隔振系统功率流的有限元计算及其传递特性研究

汤又衡，牛军川,2

（1.山东大学 机械工程学院，济南250061；2.山东大学 高效洁净机械制造教育部重点实验室，济南250061）

随着科技的进步，工程中出现了大量速度快、精度高、体型大的机械设备。振动问题愈发不可忽视。有害的振动会极大缩短机械设备的使用寿命，并降低使用精度，其带来的噪声，还对相关人员的健康带来巨大危害。如何控制振动是伴随着机械设备不断发展必须解决的一个问题。

在隔振问题的研究中，必须有更高精度的隔振模型，才能满足现阶段机械设备本身的要求。传统的隔振模型将基础和机器设备视为绝对刚体，并用只能轴向拉压的无质量弹簧和阻尼模拟隔振器，因此无法充分考虑基础和机器柔性、隔振器质量、隔振器中弯曲波等对振动传递的影响。为考虑基础弹性，宋孔杰[1]用弹性支承的刚性杆对基础进行模拟，研究了弹性基础对隔振效果的影响。随着结构的大型化和轻薄化，机器和基础的柔性问题，成为影响隔振效果的最主要因素之一，问题的研究得以深入。Snowdon[2]基于连续体模型首先研究了一维对称隔振系统基础的柔性。熊冶平[3]运用子系统导纳综合法，对非对称柔性隔振系统中柔性基础的影响进行了探讨。牛军川[4]建立柔性基础上主动隔振系统模型，并采用子结构导纳综合法建立了多激励多支承的全柔性隔振系统的一般动力学模型。

柔性基础和多维多支撑的引入给传统的隔振性能评价指标带来挑战。许多学者注意到功率流指标的优势，并将其运用于柔性基础隔振模型研究[5-7]。传统模型的基础一般采用梁板等规则结构，这是因为计算功率流时需要获得基础的导纳表达式，对于一些梁、板等简单柔性结构，通过理论计算可以获得其导纳，但对于非规则的结构，则只能使用实验的方法。但实际工程中，无论是基础还是机器，形状皆不规则，传统隔振模型在这方面缺陷明显。

数值离散方法可以很好地弥补导纳法本身的缺陷。有限元法是应用最广的数值离散方法。由于单元能按不同的联结方式进行组合，且单元本身可以有不同形状，因此可以模型化几何形状复杂的求解区域。国内有些学者也运用有限元和功率流方法，对一些简单模型进行了分析[8-10]。但是这些工作，仍旧没有涉及到不规则形状设备和基础、机器柔性、隔振器质量、弯曲波传递等诸多问题。

文中充分考虑机器、基础的不规则性和柔性，采用有限元方法将其离散，同时对隔振器采用空间梁单元建模，建立不规则形状的全柔性隔振系统的功率流计算模型，基于该模型可进一步研究各环节柔性、弯曲波等对传递功率流的影响规律，另外，采用此方法，还可以计算每一个节点处的能量密度大小，预示功率流的传递情况。

1 隔振系统动力学模型

如图1所示为全柔性隔振系统模型，机器和基础都采用弹性板来模拟，隔振器则用空间弹性梁进行建模。空间梁每个节点有6 个自由度，可以承受沿x、y、z3 个方向的力和绕x、y、z轴的力矩，从而克服了传统隔振器模型只能传播纵向波的缺陷，充分考虑弯曲波等的影响。

1.1 功率流计算

当上板受到一个点激励时，传入机器的功率流为Pin。为对其隔振性能进行评价，需进一步计算经过隔振器传递至基础的功率流Pout。传递至基础的功率可以用传递至梁末端的功率流来表示。

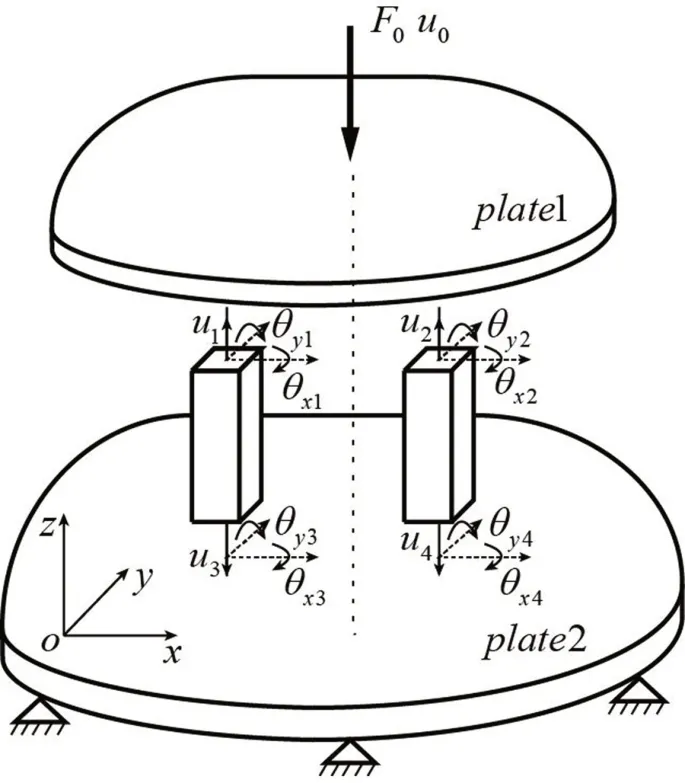
图1 全柔性隔振系统模型

文中梁和板为点接触，故而梁截面上的净功率流可以通过将梁末端节点上所有自由度的结构声强相加获得[11]，即

式中：k表示末端节点的一个自由度；Ik为k自由度的结构声强，用式(2)计算

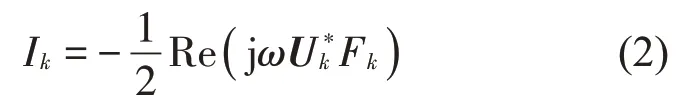
式中：j 为虚数单位；ω为角频率；Re(·)表示取虚部；（*）表示复共轭；Fk为截面处k自由度方向的广义力；Uk为截面处k方向的广义位移。则梁末端截面处通过节点p的功率流可以表示为

式中：H表示共轭转置；Fp={N,Qy,Qz,T,MyMz}T为空间梁广义力矢量；Up={u,v,w,θ,θy,θz}T为空间梁广义位移矢量。

由式(3)可知，为计算梁末端截面处的功率流，必须得到该处的力和位移响应。为充分考虑隔振器弯曲波、不规则机器和基础的柔性影响，分别采用2节点12 自由度空间梁单元及4 节点12 自由度四边形单元对隔振器、机器和基础进行划分。根据虚功原理，建立整个隔振系统的有限元离散数值模型

式中：K为系统总刚度矩阵；M为系统总质量矩阵；C=αM+βK为系统总阻尼矩阵；α、β为比例系数；U为各个节点自由度组成的广义位移矩阵；F为广义力向量。则式(4)可以化为

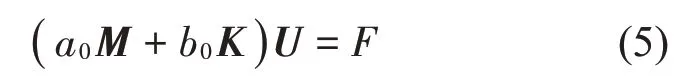
式中：a0= ( -ω2+jωα)；b0= ( 1+jωβ)。

为了求解式(5)，需要进一步计算总刚度阵、总质量阵以及广义力向量。通过总体矩阵的组装，可以得到这些要素。

1.2 总体矩阵的组装

整体组装是根据有限元耦合的思想，在梁板耦合节点处，将对应自由度的贡献相加。以如图2所示的单梁双板为例，其中左侧板为激励输入板，或振源，右侧板为功率流接收板。由于空间梁模型一个节点处有6个自由度，薄板模型一个节点处有3个自由度，故将空间梁耦合节点处的6 个自由度删减为对应板位移的3 个自由度，方便后面的总刚度矩阵的组装。

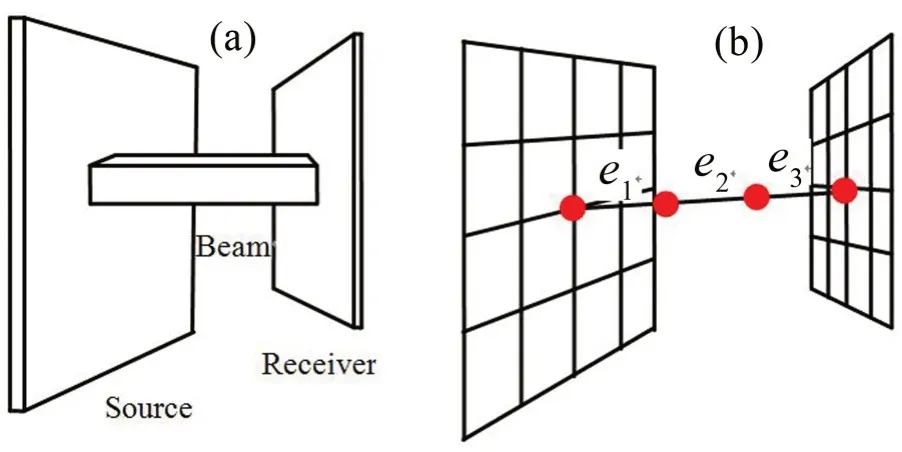
图2 梁板耦合模型

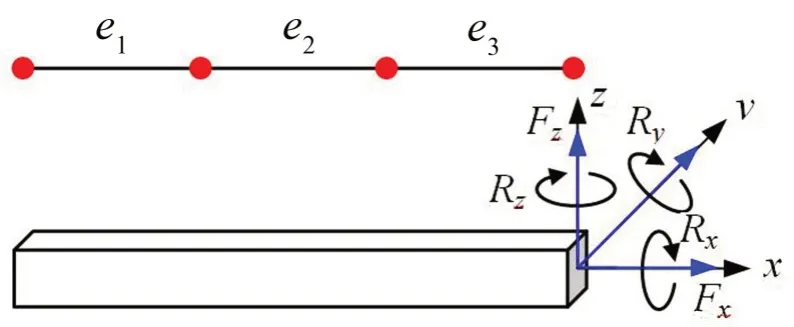
图3 空间梁单元

为求耦合节点处输入的功率流，需要获得节点处的广义位移和广义力向量。设系统总自由度数为N，梁和功率流接收板耦合节点为p，梁与输入板耦合节点为q，则总刚度阵为

式中：krp、ksq分别为接收板和振动输入板上两个耦合节点处的刚度矩阵；kbp、kbq分别为梁在两个耦合节点处对应板3个自由度的刚度矩阵；kbl表示除耦合节点外剩余梁单元组装的刚度阵；剩余节点数为l；空余部分为零元素。

总质量阵M的组装方法与式(6)中的系统总刚度阵K的组装方法相同，将总刚度阵和总质量阵代入式(5)中即可求得广义位移向量U。将式(5)写为

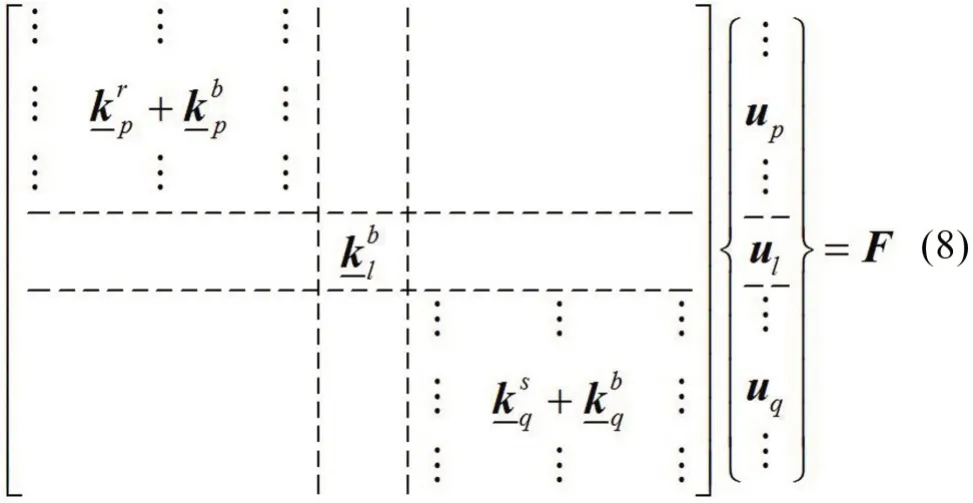
式中：up和uq分别为梁与功率流接收板、输入板的耦合节点处3个自由度的位移向量；ul为梁除耦合节点外其余各单元节点的位移向量；提取对应接收板耦合节点p的局部广义刚度阵和广义位移up，计算节点p处的广义力向量

或者

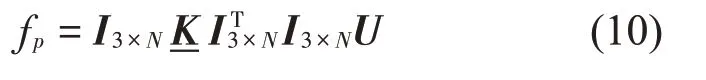
这里

将fp及up代入式(2)和式(3)即可求得传递至基础的功率流及频率平均功率流。

2 仿真与分析

传统柔性隔振模型只考虑基础柔性，将机器视为一个刚性的质量块。隔振器一般采用弹簧阻尼或者柱状橡胶隔振器模拟，忽略它们的质量，如图4所示。

图4 传统隔振器模型

这时隔振器只存在2 个轴向自由度，其单元刚度阵为

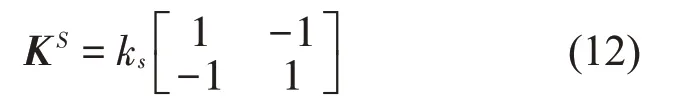
式中：ks为弹簧纵向刚度。传统模型中将橡胶隔振器视为杆，其纵向刚度矩阵仍为式(12)，式中ks=ErAr lr，Er为杆的杨氏模量，Ar为杆截面面积，lr为杆长。与12×12 的空间梁的刚度矩阵相比，传统隔振器模型缺少了2 个方向的横向弯曲刚度和绕3 个轴的扭转刚度，因此无法计及由剪力和扭矩引入的功率流。

传统隔振系统中忽略隔振器的质量，在低频隔振和隔振器质量较小时误差不大，在当今精细化程度很高的情下，小质量会引起隔振器自振，造成高频域振动传递的短路，带来极大的误差，必须加以考虑。

相比弹簧及杆模型，空间梁模型充分考虑质量的影响，兼顾6个自由度的所有信息，不仅可以传递纵向波，还可以传递弯曲波，因此比传统隔振器更精细化、更具一般性。当只考虑纵向2个自由度时，空间梁模型可以近似地退化为杆模型。进一步忽略质量矩阵，则可进一步近似退化为弹簧模型。

为对全柔性隔振系统的动力学特性进行评估，这里用板模拟机器和基础，用柔性空间梁模拟隔振器，系统参数如表1所示。

2.1 不同激励下的传递功率流

新的柔性模型，克服了只能分析纵向激励的缺陷，可以模拟横向力激励和力矩激励等，为进一步分析各种激励情况下的功率流传递带来了可能和方便。在xoy平面上，当隔振器布置对称时，不同激励形式下输入到机器和基础的功率流如图5所示。

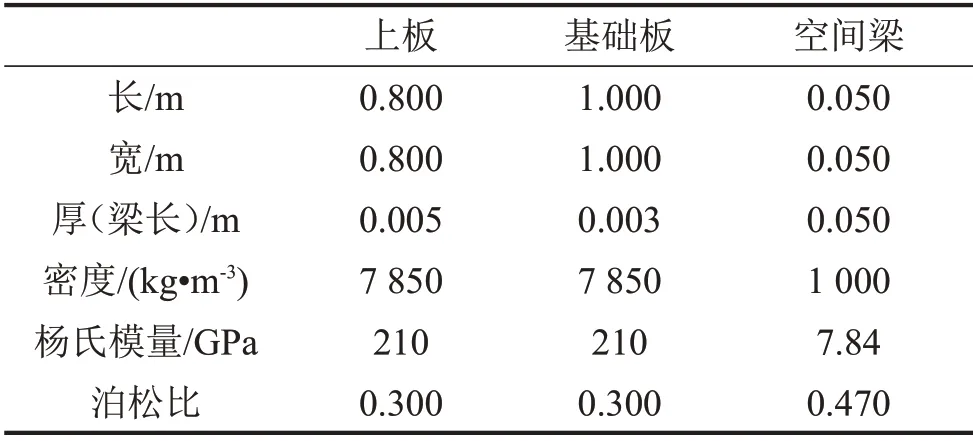
表1 模型参数

图5 不同激励形式对功率流影响

功率流曲线在低频域7.02 Hz处有一个峰值，即为机器的纵向安装频率，平面上的俯仰振动不会被激起。沿x和y向作用转矩时，低频域的0.71 Hz 处和4.97 Hz处功率流曲线出现两个峰值，分别对应机器的滚转和俯仰安装频率。3种激励情况下，低频域峰值较少，而在高频域密集出现，这是因为机器和基础的柔性参与了进来。由于系统柔性的影响，机器的曲线均在高频域出现了抬升，而传递至基础的功率流曲线则不断振荡下降。

2.2 机器柔性对传递功率流的影响

传统隔振模型一般不考虑机器柔性，全柔性隔振系统则可以进一步分析机器柔性对振动传递的影响。图6和图7所示为机器柔性对传递功率流的影响。

图6 机器不同刚度下输入机器的功率流

由图6可见，随着机器刚度的不断减小，即机器柔性的不断增加，输入机器的功率流曲线在高频域不断抬升，峰值的数量不断增加。与此同时，高频域的峰值不断向低频域移动，最终与安装频率发生耦合。由图7可见，当机器的刚度增加时，传递到基础的功率流减小，中低频处的峰值也较少。因此机器柔性对功率流存在较大影响，进行高频隔振评价时不应忽略。

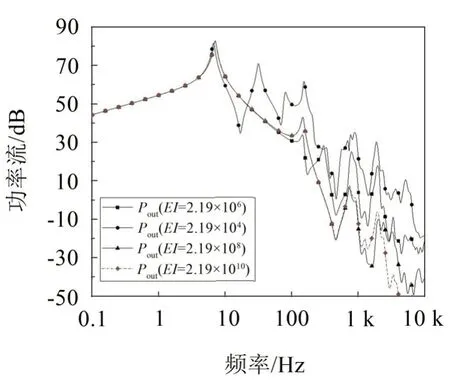
图7 机器不同刚度下输入基础的功率流

2.3 隔振器特性对传递功率流的影响

选用对称安装的全柔性隔振系统，考查隔振器参数对隔振效果的影响。为比较传统隔振系统与全柔性隔振系统，文中着重对弯曲波及质量的影响进行分析，暂不考虑阻尼的影响。图8为3种隔振器纵向刚度下输入机器和传递至基础的功率流曲线，EiA=1.96×104为橡胶隔振器的纵向刚度。当隔振器纵向刚度减小或柔性增大时，传递至基础的功率流曲线峰值增多且向低频域移动，而高频处的峰值多为基础和机器的固有弹性模态，因此变化不大。

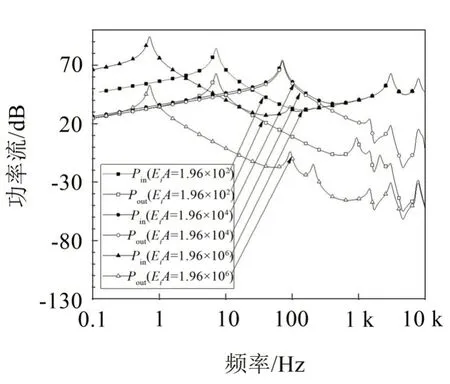
图8 不同隔振器纵向刚度下功率流传递

图9为激励非对称时不同隔振器弯曲刚度下功率流传递情况。从图中可以看出，当存在非对称激励时，隔振器会传递弯曲波，弯曲刚度对传递至机器和基础的功率流有较大影响，随着弯曲刚度的增大，第1 阶滚转安装频率对应峰值向高频域移动，逐渐接近俯仰和纵向安装频率。弯曲刚度对于更高频域的曲线影响较小。当机器承受横向载荷时，隔振器主要承受弯矩，则这时隔振器传递的弯曲波则不可以忽略。

图9 不同隔振器弯曲刚度下功率流传递

加大机器和基础的刚度，将二者高频域的峰值向高频处推移，在此基础上可以清楚地分析隔振器质量对功率流传递影响。如图10所示。

图10 隔振器质量对功率流传递影响

当隔振器密度变化时，保持隔振器尺寸或体积不变，相应质量呈正相关变化。当密度为0时，近似可以看成是无质量的隔振器模型，此时在10 Hz 至1 000 Hz 内功率流曲线平缓下降，没有峰值出现。当隔振器密度或质量不断变大时，在10 Hz 至1 000 Hz区域内峰值逐渐增多，且不断向低频域移动。这是因为隔振器的质量增加后，隔振器的自共振被激起，使功率流传递短路，原本平缓的功率流曲线陡然抬升。

3 结语

建立了一个全新的全柔性隔振模型，用薄板代替传统的刚性机器和刚性基础，用空间梁代替传统的弹簧和隔振器。采用有限元方法对各子系统进行离散，对耦合关系进行处理和组装，获得耦合点处力和位移的信息，计算输入机器的功率流及传递到基础的功率流。可以得到以下几个结论。

(1)采用有限元方法计算隔振系统功率流时，无需求取结构导纳，从而可以对不规则基础进行求解。

(2)隔振器质量对传递到基础的功率流有着较为显著的影响，会使高频域峰值增多。质量增大，峰值向低频域移动，传递至基础的功率流增大。隔振器弯曲刚度则主要影响滚转安装频率。

(3)机器柔性使得功率流在高频域明显抬升，峰值更密集，柔性的增大会逐渐影响低频域内原有的峰值。