基于分岔理论的球式自动平衡装置的稳定性研究

2019-12-27祝贵祥

噪声与振动控制 2019年6期

祝贵祥，谭青, 江波

（中南大学机电工程学院，长沙410083）

随着回转机械转子转速的不断提高，回转机械的振动直接影响着旋转机械工作的安全与可靠性[1-2]，回转机械的振动已经成为重要的研究课题之一。目前，最常见的减振方法是对转子采取高精度的动静平衡方法。但是,实际的工业生产中，回转机械在使用过程中可能会出现偏心质量分布突然发生变化的情况，动静平衡方法不能对回转机械的突变型偏心质量做到实时平衡。安装自动平衡装置是解决回转机械实时平衡的有效措施之一[3-6]。国内外学者已经提出了多种类型的自动平衡装置，其主要分为两类，一种是通过微机控制的主动式自平衡装置；另一种是通过系统自动定心原理来实现平衡的被动式自平衡装置，该类自平衡装置又分为球式、液体式、环式、摆锤式等自动平衡装置[7]。自球式自动平衡装置问世以来，该装置的研究就受到了国内外的广泛关注[8-12]。不同于液体式、环式、摆锤式等自动平衡装置[13-15]，球式自动平衡装置在高速状态下减振效益显著，且不管偏心量的位置，也不需要外界的调试和控制，其能自动发挥平衡作用[16]。

分岔分析可以很直观得到解的变化情况及解的性质发生改变的界面，使用分叉分析既可以知道系统解的变化情况，又能得到稳定平衡解存在的区域边界，同时摆脱了依靠扰动方程不能解决临界系统稳定性的困境[17]。

对某特定工况的转子，使用哪些参数才能保证自动平衡装置的稳定运行是必须考虑的问题。故研究球式自动平衡装置的行为随参数变化而改变的规律，为其设计和使用提供一个用于参考的参数可行域是有必要的。使用分岔理论研究自动平衡装置的动态特性随参数变化的演变情况，获得相应的稳定区域分布图，对于球式自动平衡装置的设计和应用具有一定的理论和实际价值。

1 球式自动平衡装置的数学模型

1.1 数学模型简要说明

球式自动平衡装置力学模型如图1所示。

图1 力学模型图

由课题组已有的研究可知，系统的运动微分方程[18]如式（1）所示

式中M为系统的总质量；m1、e为转盘的偏心质量、偏心距，m、r分别为滚球质量和半径（本文假设每个滚球的大小和质量一样）；C、K为系统的阻尼矩阵、刚度矩阵分别为滚球的角加速度、角速度、转角；I为滚球对其质心的转动惯量，单位为kg·m2；分别为转盘的角加速度、角速度、转角；稳态时转盘以角速度ω匀速转动。i为滚球个数编号，在球式自平衡装置中，至少需要一个滚球，当系统仅有一个滚球存在时，装置的平衡能力很有局限性，因此，球式自平衡装置中一般会加2个及2个以上的滚球，文中以2个滚球为例进行说明，即取n为2。β0为滚球的滚动摩擦因数，β1为滚球的黏性阻尼系数。式中变量上面的点“.”表示变量对时间的导数，后文不再说明。

当系统处于稳定状态时，滚球所受的滚动摩擦阻尼力可以忽略。此时有θ=ωt，令φi=φi+θ。

对于球式自动平衡装置，由于滚球质量是一个变化的量需要与总质量M分开，M=M1+2m+m1（M1为圆盘质量）。求出系统的偏心距和固有频率

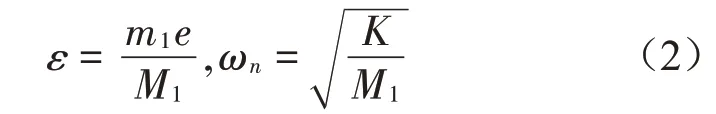
λ为滚球质量与转盘质量之比，η为转速与固有频率之比，δ为偏心距与转盘半径之比，ζ为结构阻尼比，β为黏性阻尼系数。于是有

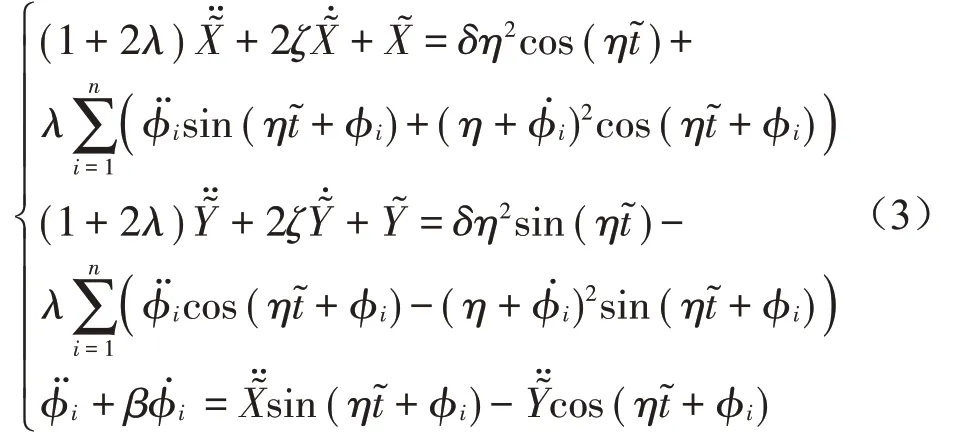
1.2 数学模型的自治化变换

根据李亚普洛夫稳定性定理，非线性自治系统的平衡解的稳定性可以用其一次近似线性方程的稳定性来进行研究[19]。研究非自治系统的分岔和稳定性问题的研究方法比较复杂，为简化问题，通过坐标变换将上述建立的非自治系统方程组转化为自治系统方程组的形式。引入旋转坐标变换，设坐标系uov的中心与轴未发生变形时中心重合并随着轴一起旋转，如图2所示。

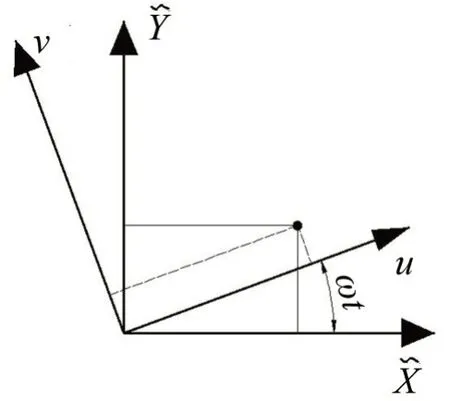
图2 旋转坐标系示意图

则有

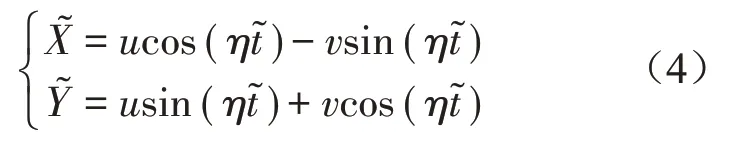
得到最终的自治化方程组为

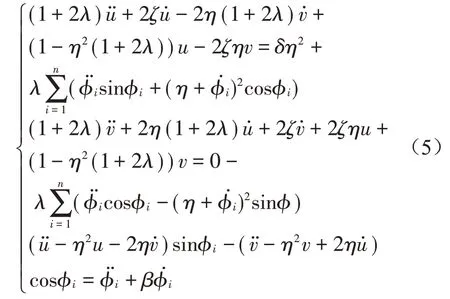
将方程组写成矩阵形式，令

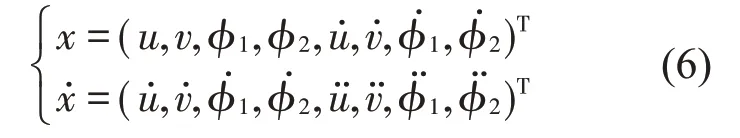
方程组可写成如下形式：B(x)x˙=D(x)，其中

Q(x)是一个满秩的且可逆的4×4方阵，I为4×4的单位矩阵，B(x)为可逆的8×8矩阵，故得到

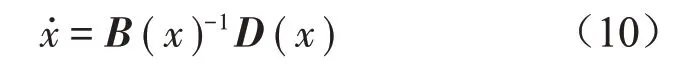
B(x)-1、D(x)都是关于向量x的矩阵，即方程组转换成了标准的微分方程组形式

2 系统的平衡解

球式自动平衡装置的数学模型可表示为一个标准形式的非线性微分方程组。由文献[20]可知，对于自治系统：x˙=f(x)；如果有a∈D（D为解区间）满足f(a)≡0则称x=a为系统的一个平衡解。

系统的平衡解反映了系统不随时间变化的平衡状态，即一种稳定的状态。

根据文献[21]，奇点时系统的速度和加速度都为零，奇点就是平衡解所对应的平衡点，故令都等于零。本文只考虑2 个球的情况，3 个球或多球的情况以此类推。令n=2，得

求解式（12）可获得平衡解1和平衡解2

（1）若u=v=0，则得平衡解1，如式（13）所示。平衡解1 状态下滚球达到理想平衡位置，实现完全减振，残余振幅为0。平衡解1 的示意图如图3(a)所示。

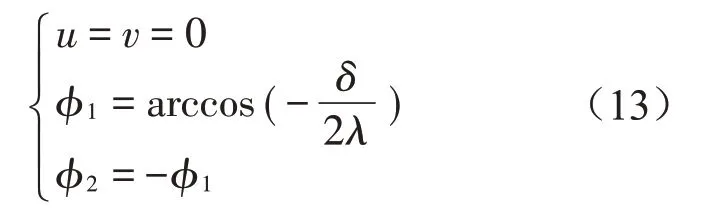
（2）若u≠0,v≠0，则得平衡解2，如式（14）所示。平衡解2状态下滚球未达到理想平衡位置。残余振幅不完全为零。平衡解2 的示意图如图3(b)所示。

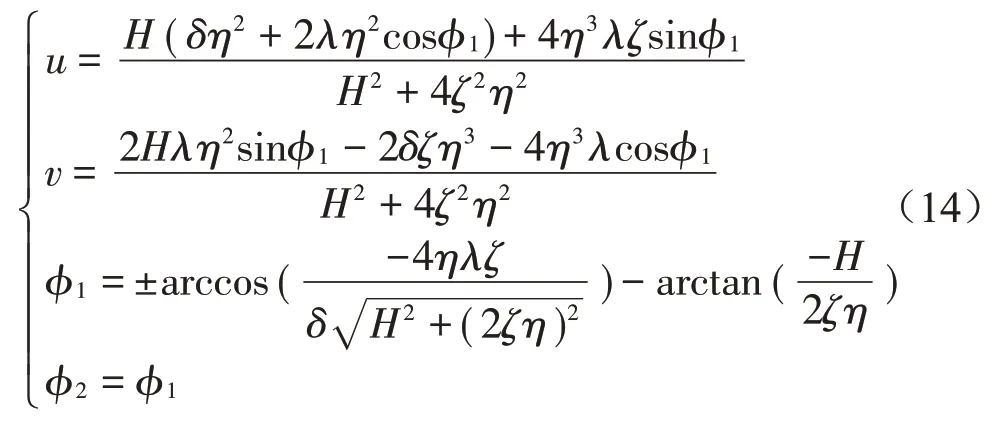
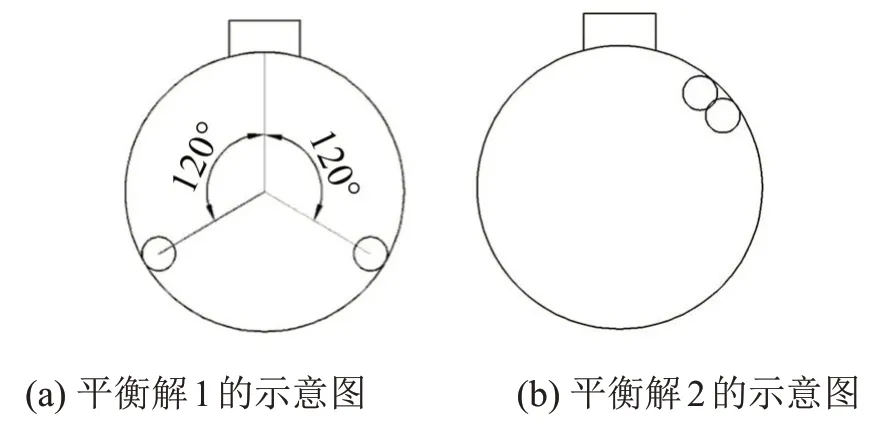
图3 平衡解的示意图

对于平衡解1，要保证滚球的相对转角φ1=有意义，只考虑偏心距为正的情况，所以（n为滚球数目），即直观上理解，滚球的质量之和必须大于等于偏心量的等效质量，当滚球处于理想平衡位置时滚球的质量必须足够用来补偿偏心质量，这样才能实现完全减振。

考察平衡解2(±)的表达式，要保证解的存在性，则可得式（15），可以看出在时，不等式恒成立,即平衡解2(±)在时一直存在。当时，对于η→∞，除的区域，不等式成立。

解2(-)为平衡解2 中滚球相对转角表达式前面取负号

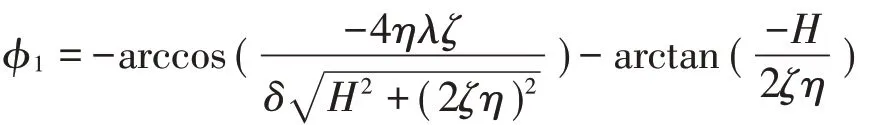
解2(+)为表达式取正号：

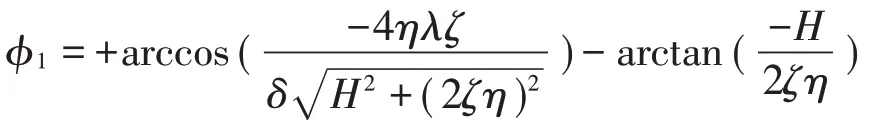
根据李雅普诺夫稳定性定理，对于形状如x˙=f(x)的自治非线性系统平衡解的稳定性分析可以通过对其一次近似线性方程的平衡解的稳定性研究实现。其一次近似方程为

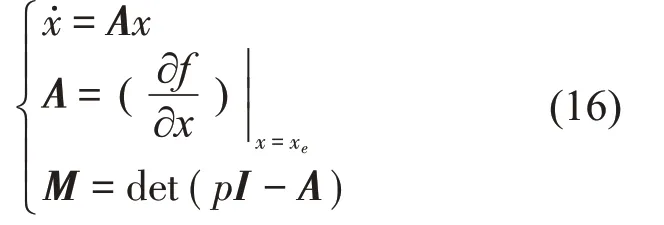
其中矩阵A为系统在平衡解xe的雅克比矩阵，M为其雅克比矩阵的特征方程，p为特征值。根据李亚普洛夫定理和劳斯判据，系统平衡点稳定的充分必要条件是特征方程的所有特征值的实部都为负数，即：real(pj)＜0,j=1,2,…,N。N为系统的阶次，pj为系统的第j个特征值。若该一次近似系统只要有一个特征值取正值，对应的非线性系统的平衡解也就不稳定。同时，李亚普洛夫也指出当一次近似系统的特征值出现纯虚根，即在该参数空间中系统为临界稳定系统时的情况。

运用MATLAB 计算雅克比矩阵和特征值矩阵十分方便和迅速，故直接利用劳斯判据。根据平衡解1和平衡解2的表达式，获得平衡解关于参数空间的关系式，代入至雅克比矩阵中，从而解出特征值矩阵，判断所有特征值的实部是否小于0 从而判断稳定性。

分别设置参数空间中不同的参数为自由参数（双参数或者多参数）进行迭代，从而得到稳定域。具体流程见图4

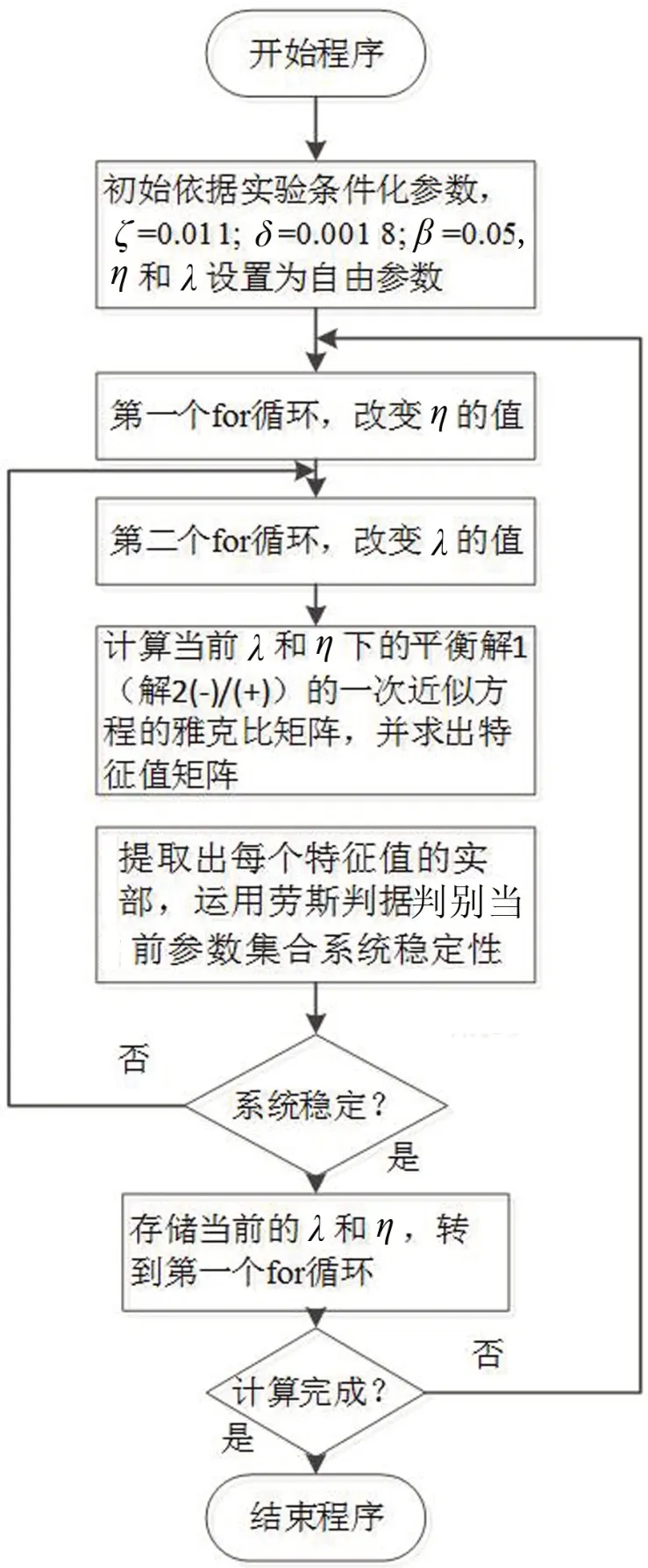
图4 平衡解的稳定边界计算流程图

经过计算得到η-λ、η-δ、η-ζ、η-β双参数下的平衡解1和平衡解2(±)的稳定区域分布图，结果如图5至图8所示。

不稳定区域外不存在稳定平衡解的区域。平衡解1为滚球达到理想平衡位置，实现完全减振，残余振幅为0；平衡解2(±)下残余振幅不为零。

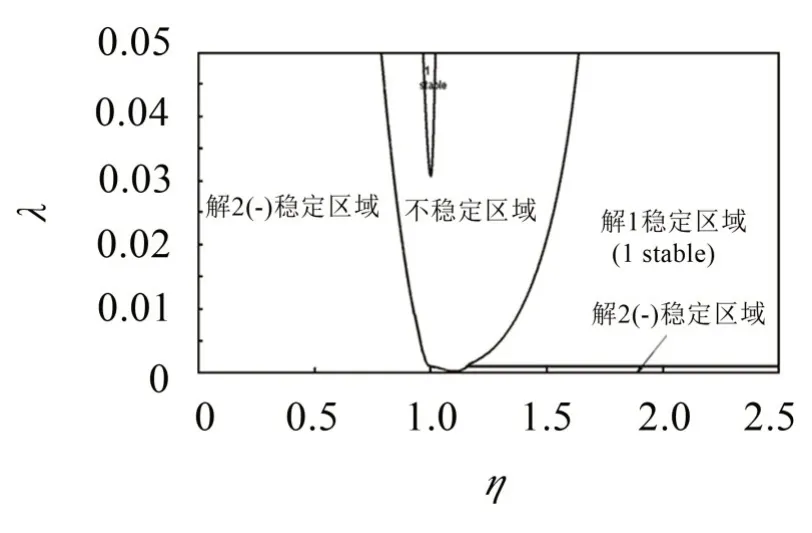
图5 η-λ双自由参数下的稳定区域

从图5可以看出，亚临界转速下有稳定的平衡解2(-)存在，解2(-)在亚临界转速下滚球的相对角度是偏向于偏心质量一侧的（当λ=0.0018,δ=0.0018,ζ=0.011 ，β=0.0814 ，η=0.95 时，φ1=-0.666 rad=-38.16°）。在亚临界转速下，随着滚球质量占比的增大，系统将更早进入不稳定区域，这时滚球相对于转盘开始运动。当滚球质量较大时(λ＞0.03)，会在转速比为1 附近的狭小区域内（例如λ=0.05时，0.969 9 ＜η＜1.023）产生稳定的平衡解1，不过这个区域太过狭小，转速一旦稍微升高，平衡状态立即消失。在过临界转速下，滚球质量越大，进入稳定区域所需要的转速越高，当λ=0.049 8 时，η≥1.639才能进入平衡解1存在的稳定区域。当滚球质量之和不能完全抵消偏心质量造成的偏心时，在过临界转速下，会有稳定的平衡解2(-)存在，这时两个滚球靠在一起分布于偏心质量对侧，一定程度上抑制系统振动但仍然存在残余振幅。

图6 η-δ双自由参数下的稳定区域

从图6可以看出，当偏心质量比较小，在亚临界转速下即开始出现不稳定区域，滚球相对于转盘转动，偏心质量增大，开始出现稳定的平衡解2(-)。当转速η≥1.21，进入平衡解1的稳定区域。

从图7可以看出，当系统的结构阻尼较大时，在亚临界系统提前进入不稳定区域，滚球相对于转盘转动。在过临界转速下，当结构阻尼比较小时，系统需要更高的转速才能进入解1的稳定区域内实现减振（如ζ=0.000 5,η=1.403）。

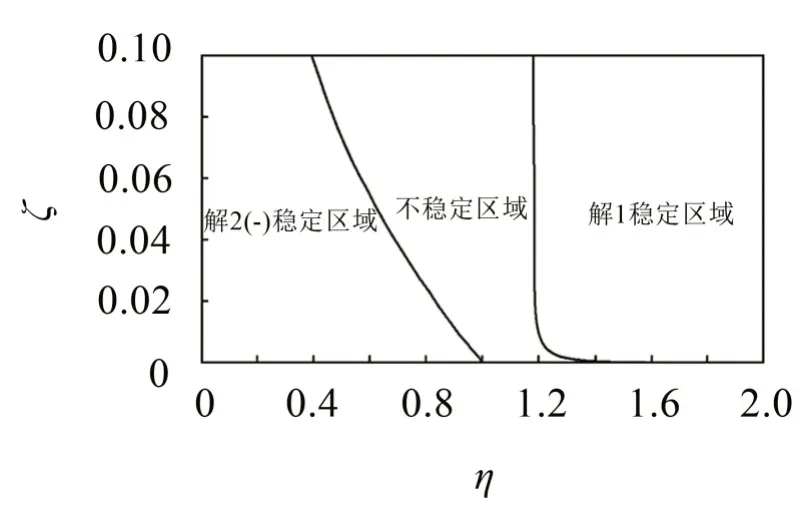
图7 η-ζ双自由参数下的稳定区域

图8 η-β双自由参数下的稳定区域

从图8可以看出，在亚临界转速下，平衡解2(-)的稳定区域与不稳定区域的分界线是η=0.885 4的一条垂直线，在过临界转速下，当黏性阻尼系数比较大的时候，在转速大于1.208时进入平衡解1的稳定区域内。但当β比较小时，系统需要更大的转速才能进入解1的稳定区域（β=0.000 5,η=1.465）。

3 实验研究

实验研究是对η-λ、η-δ、η-β双参数分岔和稳定性的理论分析进行验证。本文设计、搭建了如图9（a）所示的实验平台；振动信号采集系统用来记录实验过程中的振动情况，振动信号采集系统如图9（c）所示。

（1）验证η-λ双参数分岔和稳定性分析结论时，用不同质量的滚球来平衡系统，观察系统平衡解1的稳定性的变化情况。将电机的转速调至该滚球质量对应的根据理论计算得到的转速值附近，然后施加冲击扰动，改变滚球质量，观察装置的稳定性情况，实验结果如图10所示。

图10中相等质量下的稳定点表示在该质量和转速工况下，系统处于稳定状态，冲击扰动后系统不会失稳。不稳定点表示系统在冲击扰动后会发生失稳现象。

从图10中可以看出，滚球处于稳定点时，系统的振幅只有0.02 mm。当系统处于不稳定点，施加冲击扰动后系统开始失稳，最后完全失稳，此时的最大振幅可达到0.35 mm，振幅明显增加。从图中可知，当m=7.10 g时，实验中开始出现失稳的不稳定点η实验=1.243；当m=32.12 g，实验的开始出现失稳的不稳定点η实验=1.363。实验显示了随着滚球质量的增大，开始出现失稳的不稳定点增大，说明滚球越大，系统越晚进入稳定区域，这与理论分析的结论显示的趋势是一致的。

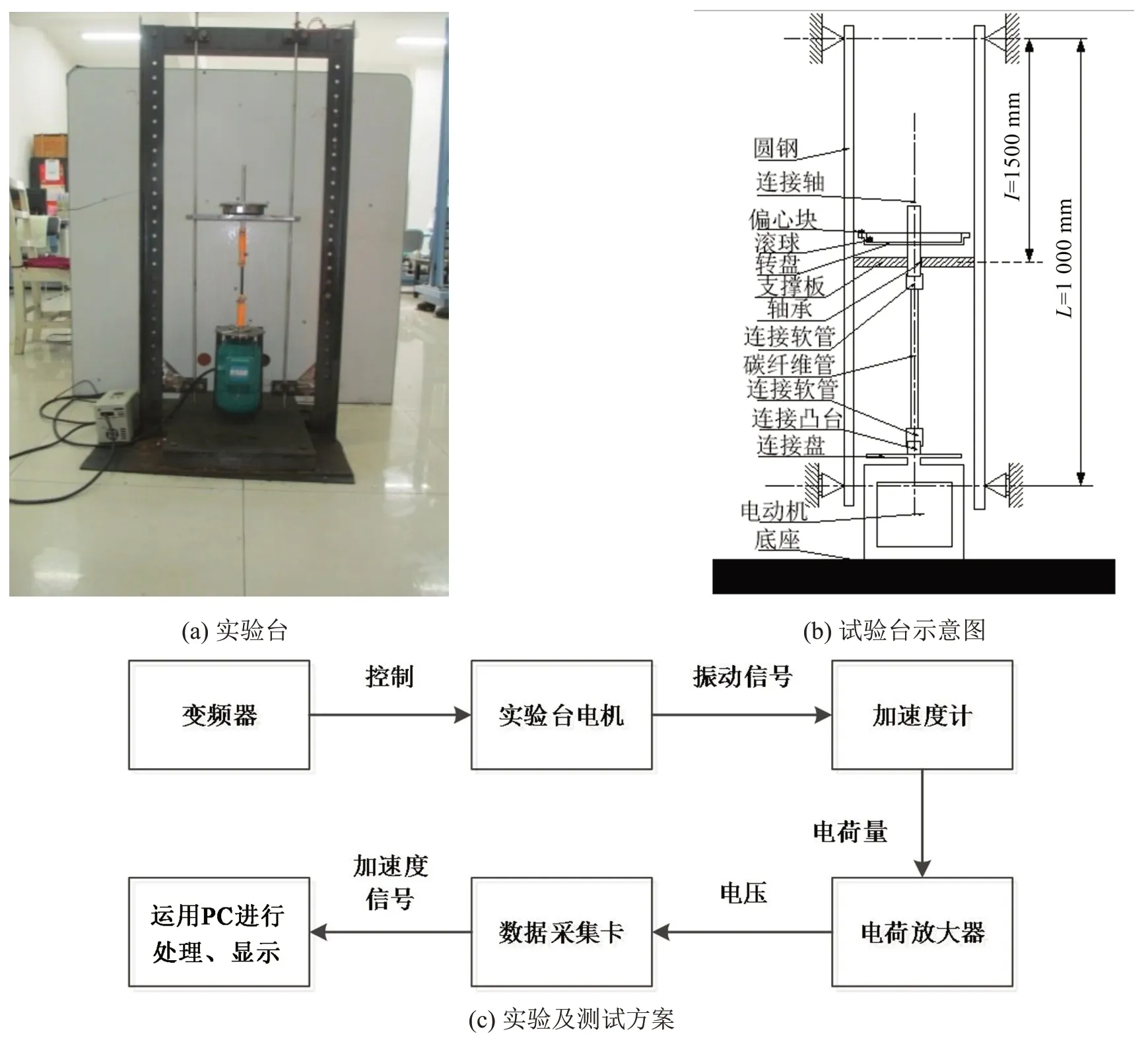
图9 实验台及实验方案

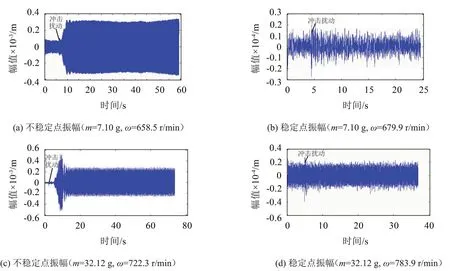
图10 不同滚球质量工况下的稳定点和不稳定点的振幅

（2）验证分岔现象的存在以及η-δ双参数分岔和稳定性分析结论，文中改变偏心量大小，观察系统稳定性的变化情况，本次实验使用的滚球质量为32.12 g。用两组不同偏心质量做稳定性试验，试验结果如图11所示。

从上图可知，当偏心质量为3 g 时，实验中开始出现失稳的不稳定点的转速比η实验=1.316；当偏心质量m1=35 g，实验中开始出现失稳的不稳定点η实验=1.355。理论值和实验结论基本一致。实验显示随着偏心质量的增大，不稳定点的频率稍有增大，说明偏心量的大小对进入平衡解1的稳定区域影响不是很明显。

（3）验证η-β双参数分岔和稳定性分析结论。根据摩擦学理论，向轨道中加入不同黏度的润滑剂来研究黏性阻尼的双参数分岔和稳定性问题。实验中使用的滚球质量为32.13 g，分别在46#液压油、低黏度油、不加油3种条件下做了3组试验。实验结果如图12所示。

通过实验发现，对于使用40#液压油的轨道，滚球在超过ω=713.6 r/min 的转速下能处于稳定的平衡解1的状态。使用低黏度的润滑油的轨道黏性阻尼较小，滚球很难稳定下来，系统一直未稳定。当不使用润滑油时，轨道具有很小的黏性阻尼和较大的滚动摩擦阻尼，系统一直未稳定。因此，在轨道中加入足够黏度和剂量的润滑油对提高系统减振效果和稳定性具有重要意义。

4 结语

球式自动平衡装置需要在不同工况下稳定运行。在使用过程中部分参数可能发生变化，如偏心量大小和位置、转速、结构阻尼等。因此，研究系统在参数变化情况下动态特性的变化规律是有重要意义的。本文引入无量纲变量和旋转坐标系对数学模型进行无量纲化和自治化处理。利用微分方程理论求出自治系统的平衡解1和平衡解2(±)，根据李雅普诺夫原理和劳斯稳定性判据判断平衡解的稳定性变化情况，获得了η-λ、η-δ、η-ζ、η-β双参数下的平衡解1 和平衡解2(±)的稳定区域。通过研究得到了平衡解随转速、滚球质量、偏心距等参数变化而变化的趋势图。