基于Catia的转向力矩波动仿真及相位角设计

刘忠侦，庄英武，宋俊良，姜旭春

基于Catia的转向力矩波动仿真及相位角设计

刘忠侦，庄英武，宋俊良，姜旭春

（恒大恒驰新能源汽车研究院（上海）有限公司，上海 201600）

转向系统性能作为整车性能的一部分，是驾驶人员最直接、最容易感受的属性，但力矩波动又是转向系统性能重要的因子，它直接影响驾驶员对车辆的感觉，因此解决好力矩波动非常关键。同时，力矩波动波峰波谷所处位置，对驾驶感也是特别重要的评价因素。文章阐述了力矩波动的计算方法及Catia仿真，并介绍如何设定转向系统相位角。

转向管柱；中间轴；相位角；力矩波动；Catia

前言

中间轴作为转向系统传动机构中的基本部件，它起着将转向管柱力矩传递给转向器的桥梁作用，而中间轴一般采用双十字轴万向节的结构[1]。由于中间轴采用十字轴万向节结构，为非等速传动，因此会产生传动力矩波动。该波动影响驾驶员对转向系统的主观感觉，引起驾驶员的不舒适和疲劳，给驾驶带来潜在危险[2]，也影响着传动部件的寿命。特别地，如果该力矩波动在转向盘中心位置左右不对称，将严重影响驾驶员的驾驶感，如图1所示曲线。因此，前期转向系统设计开发时，需规避这种问题，将力矩波动控制在一定范围内，并通过中间轴相位角的布置，使力矩波动的波谷置于舒适位置。

对转向系统力矩波动的研究，在不少资料都有体现，方法手段也各有差异，有的采用Adams，有的采用Matlab。但采用此两个软件分析，不能很好地对相位角进行调整布置。随着企业越来越普及Catia，利用Catia对转向系统进行力矩波动分析将非常便利。

本文介绍Catia作为力矩波动分析手段，及对比其分析的可信度，并介绍如何调整中间轴十字轴万向节布置，使力矩波动波谷处于转向盘中心位置。

图1 力矩波动曲线

1 力矩波动的理论计算[2]

转向管柱带中间轴一般为三段式结构。为保证传动平滑，必须给中间轴赋予一定的相位角。在评价中间轴相位角时，我们可以这样考虑：当其等效夹角取得最小值的时候，设定的中间轴相位角是最优的相位角（中间轴下端的十字叉相对中间轴上端的十字叉顺时针转过角度ψ，观察方向从驾驶室端至转向器），下面按照等效夹角计算力矩波动情况。

根据瞬时功率相等条件，从动轴上的转矩为[3]：

T2＝T1*[ (1－sin2βe cos21)/cosβe] （1）

式中：βe --等效夹角；1--输入轴转角；T2--输出转矩；T1--输入转矩

①当1＝90°和270°时，从动轴上的转矩达到最大值：T2max＝T1/cosβe

②当1＝0°和180°时，从动轴上的转矩达到最小值：T2min＝T1*cosβe

因此整个管柱的力矩波动范围为：（cosβe-1）～（1/cosβe-1）。

其中，对于多段式的空间布置的传动轴，考虑相邻轴的计算，可按照下列公式求得相邻三段轴的等效夹角[4]：

βe2=((β12-β22cos (2(α+ψ)))2+

β24sin2(2(α+ψ)))1/2（2）

α——输入轴和中间轴所在平面与中间轴和输出轴所在平面的夹角；

1——为管柱与中间轴夹角；

2——为中间轴与转向器输入轴夹角；

ψ——中间轴下端连接叉的相位角。

因此，三段式传动轴可以等效为两段式传动形式，则力矩波动W：

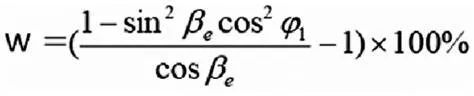
2 Catia力矩波动仿真

CATIA是法国达索公司开发的旗舰产品。作为PLM协同解决方案的一个重要组成部分，它可以通过建模协助设计概念产品，并支持从项目前阶段、具体的设计、分析、模拟、组装到维护在内的全部工业设计流程。它在汽车领域被广泛、普遍运用。本文用Catia V5中DMU模块对本主题进行分析。

为了叙述方便，本文将转向管柱外部部件简化，只保留了转向柱芯轴、中间轴总成部分，如图2所示。

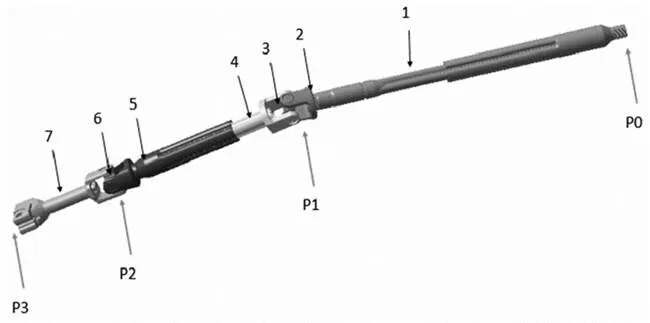
1. 转向柱芯轴；2.上节叉；3.十字轴I；4.中间轴及节叉I；5. 中间轴及节叉II；6.十字轴II；7.输入轴及节叉P0为管柱上端点；P1为管柱与中间轴连接十字轴中心点；P2为中间轴与转向器输入轴连接十字轴中心点；P3为输入轴线任意一点

运动副设定：

为了方便后续处理约束，需设置两个虚拟地面做部件，可命名为“Upper Ground”和“Lower Ground”，并装配到Product中。

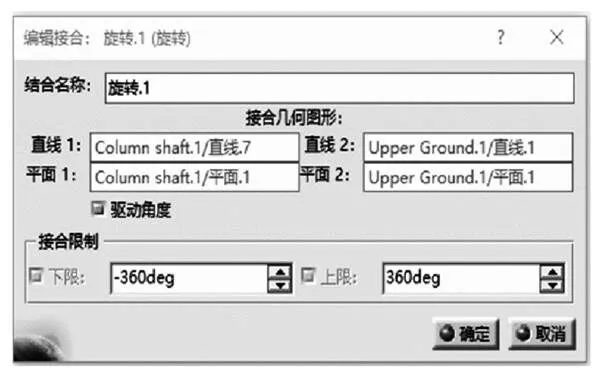
图3 旋转副创建示图

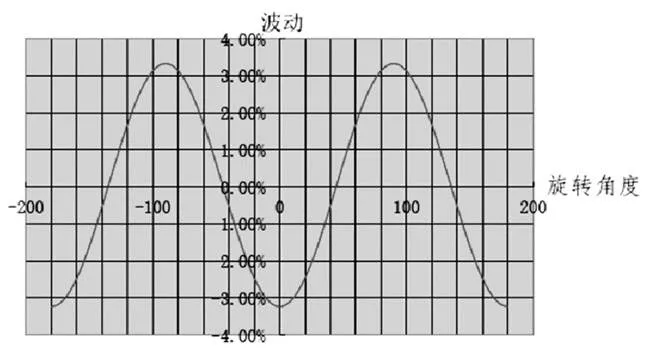
图4 力矩波动曲线

将所有部件在Product下装配完成，切换到DMU状态。点击固定图标，固定“Upper Ground”。点击旋转副，创建转向柱芯轴1与“Upper Ground之间的旋转副，并添加驱动，如图3所示。采用相同方式，用旋转副，创建转向柱芯轴1与上节叉2之间的旋转副，为了后续调节上节叉2位置，因此本旋转副也需添加驱动。随后，设定上节叉2与十字轴I、十字轴I与中间轴及节叉I、中间轴及节叉II与十字轴II、十字轴II与输入轴及节叉、输入轴及节叉与Lower Ground为旋转副，无需加驱动。中间轴及节叉I与中间轴及节叉II用移动副约束。最后两个虚拟地面“Upper Ground”与“Lower Ground”用固接副约束。最终运动副自由度为0，可以实现仿真运动。

3 计算分析

为了验证Catia力矩波动仿真的可靠性，本文以国内某车型转向硬点为例作分析说明，转向硬点P0（2660.16，-380，1119.46），P1（2253.30，-380，925.33），P2（2068.9，-366.23，753.27），P3（1975.2，-340.24，639.38）。

3.1 力矩波动理论计算分析

根据式（2）、（3），可运用Matlab编程计算力矩波动，也可利用office中excel的强大计算，编制计算器。本文即利用excel做计算器，计算结果如图4示。

计算结果力矩波动为：-3.23%～3.33%，满足小于5%的要求。

3.2 Catia DMU仿真分析

根据上文设置完成的约束副，点击模拟命令图标，仿真命令设置如图5所示。点击激活传感器，弹出传感器界面，选择旋转副1和8作为观察对象。运动仿真结束后，输出excel文件，处理得到波动曲线。其中波动需做计算处理：w=(1-Δθ输入/Δθ输出)/2，部分数据如图6所示。

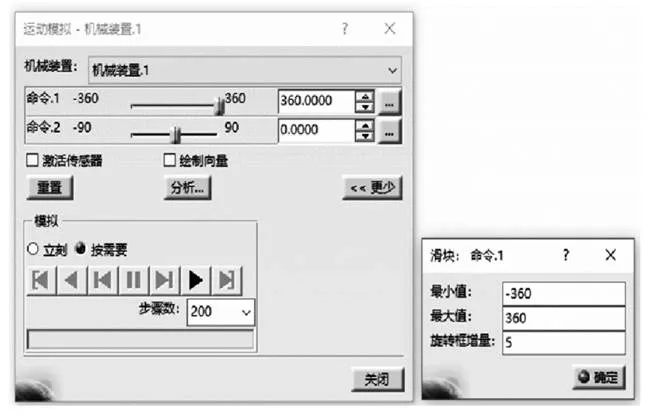
图5 运动仿真命令设置示图

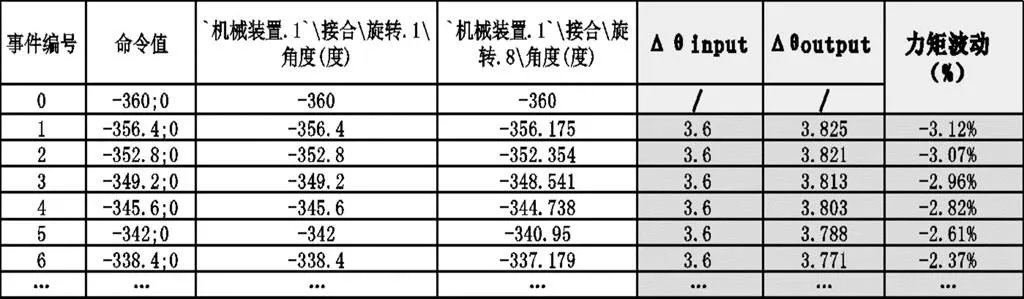
图6 波动部分数据

仿真结果如图7所示，波动为：-3.13%～2.94%，但初始位置力矩波动的波谷偏离方向盘中心位置。

图7 力矩波动曲线

3.3 理论计算与Catia仿真结果对比分析

由理论计算和Catia仿真结果对比可知，两者差异很小，如图8对比曲线，说明两者均可作为计算转向力矩波动的一种方法。

力矩波动如果超过5%，则会影响驾驶感。转动方向盘时，有忽轻忽重感。因此，如果没有满足小于5%的波动范围，则需重新优化转向硬点，直至波动小于5%为止。

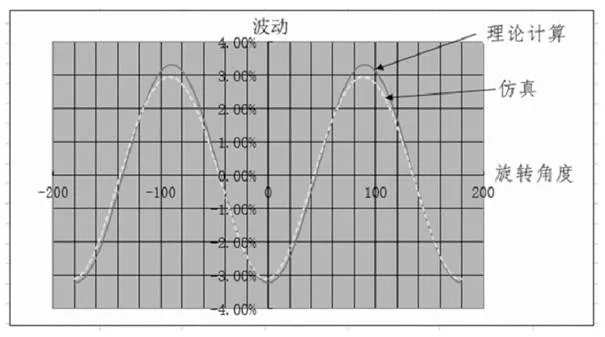
图8 力矩波动对比图

3.4 相位角的设计布置

为了使力矩波动最小，除了对转向硬点布置优化，相位角的设计也非常关键。根据计算公式（1）、（2）可知，当α+ψ=0°或α+ψ=180°时，βe取得最小，力矩波动也最小。因此我们可以从理论计算方法得到相位角ψ值。

通过上文对力矩波动的理论计算和Catia仿真，如果波动曲线满足小于5%的要求，则可进一步对波动曲线优化，让曲线的波谷处于方向盘中心位置，使驾驶员左或右打转向，有力的梯度感，而不能出现左轻右重或者左重右轻，不对称现象。这也是为什么要将力矩波动波谷设定在方向盘中心位置，而不是波峰或曲线其它位置点作为方向盘中心位置的原因。

Catia DMU仿真的可视化，使得观察和调整中间轴节叉及相位角的布置非常方便。本文通过调整节叉2的布置（但维持相位角不变），使力矩波动曲线相应地调整到我们需要的位置。如图9所示，调整命令2按键，即可使波动曲线的波谷调整到中心位置（调整的数值根据波谷时实际偏离0点的角度，这个数据可以从仿真导出的结果中读取）。

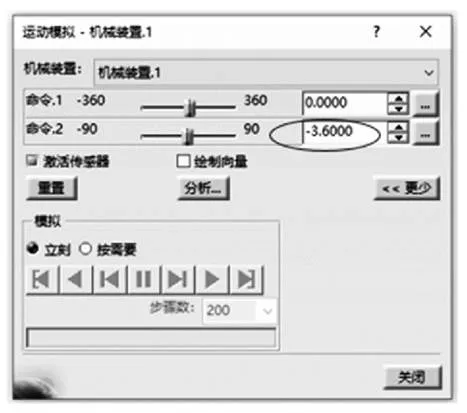
图9 调整角度命令图

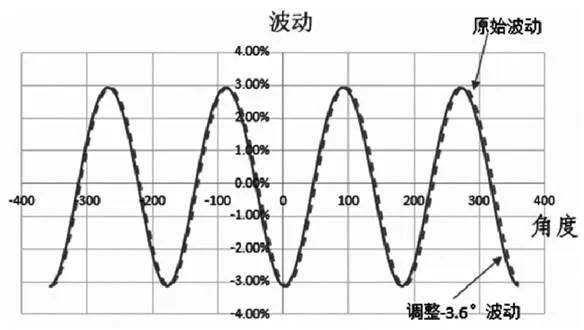
图10 调整角度后曲线

中间轴上节叉2调整相对管柱角度布置后，力矩波动的波谷调整到了“0”点位置，即方向盘中心位置，如图10所示（由于本案例初始中间位置波谷距离中心位置很近，因此调整角度很小）。

4 总结

本文介绍了转向管柱力矩波动的理论计算方法，同时也详细介绍了Catia DMU约束副的设定、仿真以及仿真结果的输出。通过对比分析理论计算和仿真的结果，说明了两个方法的正确性。但实际工作中，为了提高工作效率，减少数模修改，一般先采用理论计算的方式分析力矩波动，根据计算结果指导、优化转向硬点，待力矩波动满足要求后，锁定转向硬点，即可进行细化数模工作，并利用DMU仿真指导调整中间轴相位角布置，使力矩波动波谷处于方向盘左右对称位置。

[1] 刘惟信.汽车设计[M].北京.清华大学出版社.2001.

[2] 裴锦华.汽车转向系统力矩波动的匹配研究[J].汽车科技,2010.

[3] 王宵锋.汽车底盘设计[M].北京.清华大学出版社.2010.

[4] 高新华等.基于代理模型的轿车转向柱力矩波动关系研究与优化[J].数字化设计,2008.

The torque fluctuation of steering system base on Catia simulation and phase angle design

Liu Zhongzhen, Zhang Yingwu, Song Junliang, Jiang Xuchun

（Evergrande Heng Chi New Energy Automotive Institute (Shanghai) Co., Ltd., Shanghai 201600）

As a part of the vehicle performance, steering system performance is the most direct and easily felt attribute of drivers. But torque fluctuation is one of the most important steering system factors. It directly affects the driver's perception of the vehicle, so solving the torque fluctuation is very critical. At the same time, the location of the peak and trough of torque fluctuation is also an important factor to driving feeling. This paper describes the calculation method of torque fluctuation and Catia simulation, and introduces how to design the phase angle of steering system.

Steering column; Intermediate shaft; Phase angle; Torque fluctuation; Catia

U467

B

1671-7988(2019)24-82-04

U467

B

1671-7988(2019)24-82-04

10.16638/j.cnki.1671-7988.2019.24.027

刘忠侦（1979-），男，就职于恒大恒驰新能源汽车研究院（上海）有限公司，从事底盘转向研究与开发。