在辨析中明理，在纠错中提高

湖北省武汉第三寄宿中学 陈祖华

问题：对于题目“一段抛物线M∶y=-x（x-3）+c（0≤x≤3）与直线m：y=x+2有唯一公共点，若c为整数，确定所有c的值”，甲的结果是c=1，乙的结果是c=3或c=4，则（ ）.

A.甲的结果正确

B.乙的结果正确

C.甲、乙的结果合在一起才正确

D.甲、乙的结果合在一起也不正确

这是2018年河北中考数学试题中的一道选择题，我们在九年级一次考试中引用，发现错误率很高，引起了我们数学备课组的关注.一直以来，总让学生觉得数学难学，作为教者的我们，在教学过程中是否尊重学科知识的规律？是否尊重学生的认知规律？是否能让教而不会的悲剧少重演？这些应是我们长期深度思考的问题.为还原真相，现将课堂部分整理再现，以利于和各位同仁探讨数学教学的有效性，共同提高课堂的效率.

一、课堂过程再现

1.辨析之争

由抛物线y=-x（x-3）+c（0≤x≤3）与直线y=x+2有唯一公共点，得Δ=b2-4ac=（-2）2-4（2-c）=4c-4=0，则c=1.所以选A.

生2：抛物线y=-x（x-3）+c（0≤x≤3）可以看作将抛物线y=-x（x-3）向上（c＞0）或向下（c＜0）平移|c|个单位得到的：

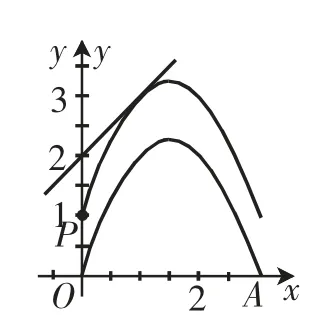
图1

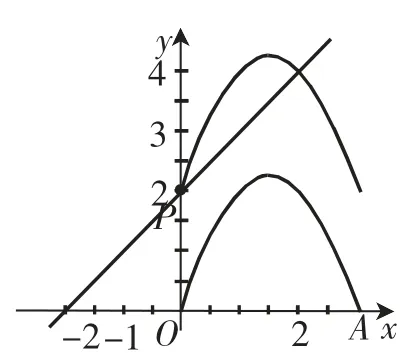
图2

抛物线M∶y=-x（x-3）+c（0≤x≤3）与直线m∶y=x+2有唯一公共点，若c为整数，确定所有c的值的问题，可以直观用图1～5分别表示将抛物线向上平移1个单位、2个单位、3个单位、4个单位和5个单位而得到.其中图2是向上平移2个单位的情况，与已知直线有2个公共点，不合要求，应舍去.故c的值应为1、3、4、5.

图3

图4

对于生1与生2的解答，如何评价？全班57人中有39人支持生1，占比68.4%，他们认为按题意，生1已经解答得很好，直接联立方程，顺理成章.但有27人，不能排除生2的解法错误，认为生2利用平移直观解释了本题解的情况，在生1和生2的矛盾解答中无法判断谁对谁错.

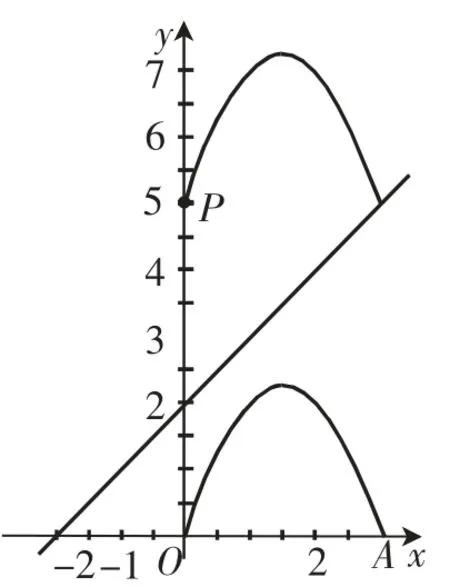
图5

在激烈的争辩中，我在课堂中让学生进行了小组互动学习，通过讨论，有学生对生1的解法提出了批判：问题的关键是抛物线自变量的范围起了作用，虽然此抛物线与直线有唯一公共点，但这个公共点可能不在所给的定义域内.此时，全班不自觉地响起了掌声，生1解答的局限性得到明确.

2.“意外”收获

当全班学生还沉浸在生2解法的收获之时，部分不服输的学生已开始了深入研究.

图6

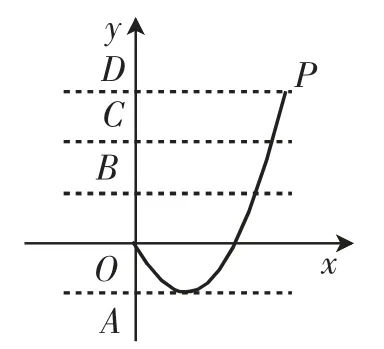
图7

生4：（不依不饶并跃跃欲试）按生3的想法，我们不妨做些变式.由得x2-2x+2-c=0.我们可以将x2-2x+2-c=0看成的公共解的情况.即求抛物线y=x2-2x（0≤x≤3）与直线y=c-2（c为整数）的唯一公共点情况.我们可以利用图7，显然发现c-2的值为-1、0、1、2、3，得c的值为1、2、3、4、5.

3.“百花齐放”

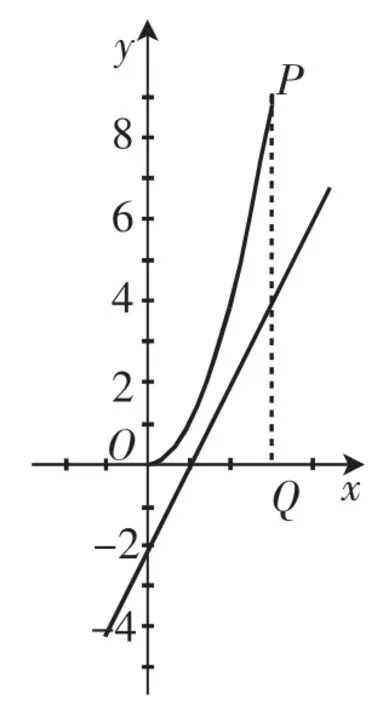
图8

图9

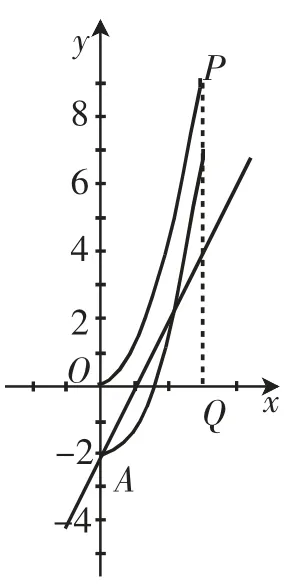
图10

图11

图12

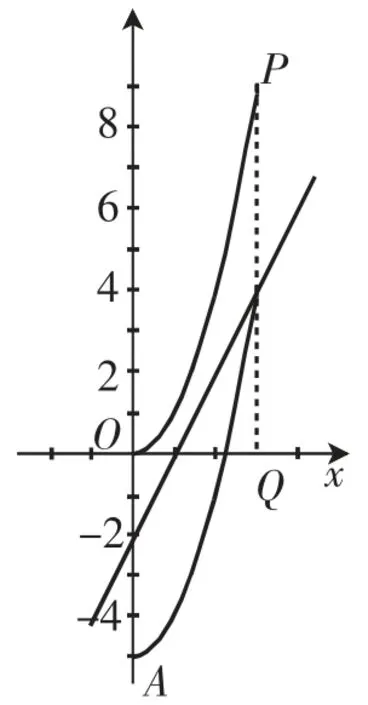
图13

其中图10反映的是-c=-2，即c=2时的情况，不合题意，应舍去，也可以得c的值为1、3、4、5.

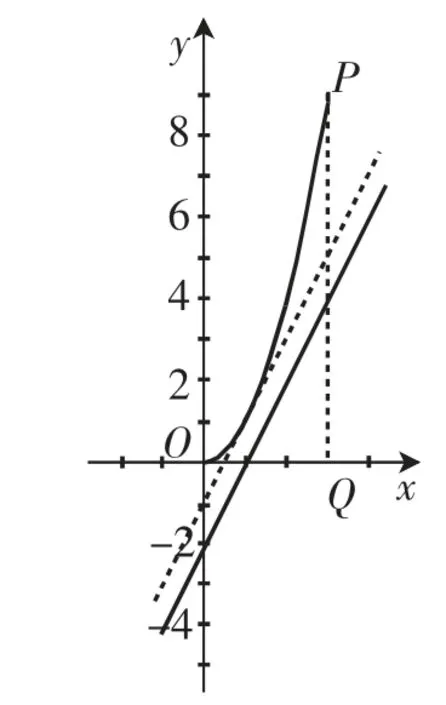
图14

图15

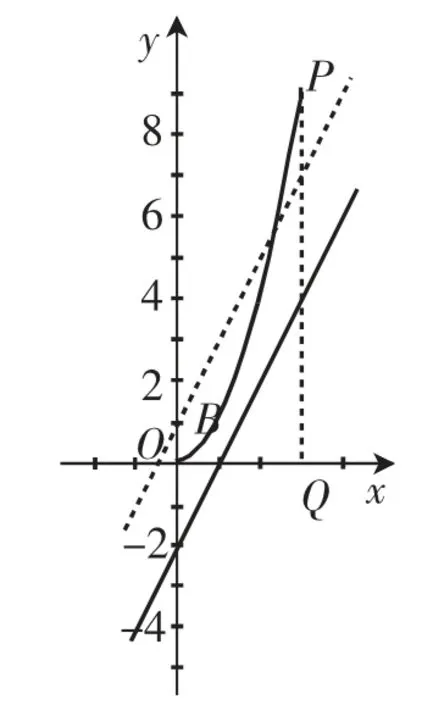
图16

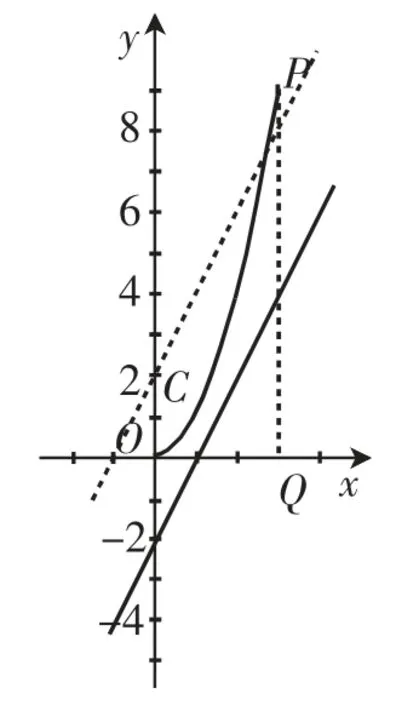
图17

图18

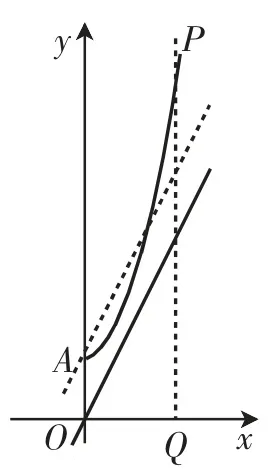
图19

图20

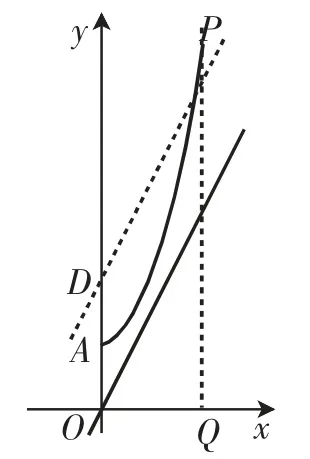
图21

图22

不得不佩服学生的学习能力.当点燃了学生思维的火花，学生的创新能力、自主探究能力被成功唤醒，在这种积极的思维状态下，就是难的问题他们也觉得简单.通过变式，改变二次项和一次项的不同位置，从正向和逆向两个方面，进行了全面变换，从本质上解决此问题超出了教学的预设.

二、意外的惊喜

有时候，当一种方法被学生掌握并利用时，会带来很多意外的惊喜，让你感觉到学生实实在在的获得感与进步，这时教育的效果才真正体现：

⑴当a≤x≤a+1时，函数y=x2-2x+1的最小值为1，求a的值.

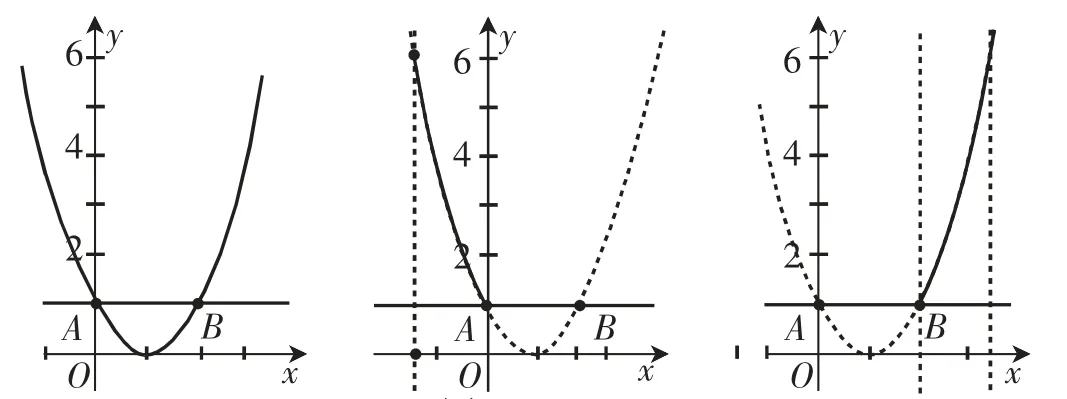
图23

这是在解决了前面的问题后学生直接得出的结果.显然点A、B即为y=1这条直线与已知抛物线y=x2-2x+1的交点，分a≤x≤a+1在抛物线对称轴左侧和右侧两种情况，直接发现a+1=0或a=2，得a的值为-1或2.不得不说的是，这种题，过去讲了很多，学生一直觉得难.

⑵如图24，已知抛物线m∶y=-x2+bx+3与x轴交于A、B两点（点A在点B的左边），交y轴于点C，其对称轴为直线x=1，抛物线n经过点A，与x轴交于另一点E（5，0），交y轴于点

①求出抛物线n的解析式.

②点M为抛物线n上一动点，作MN∥y轴，交抛物线m于点N，求点M自点A运动到点E的过程中，线段MN的最大值.

图24

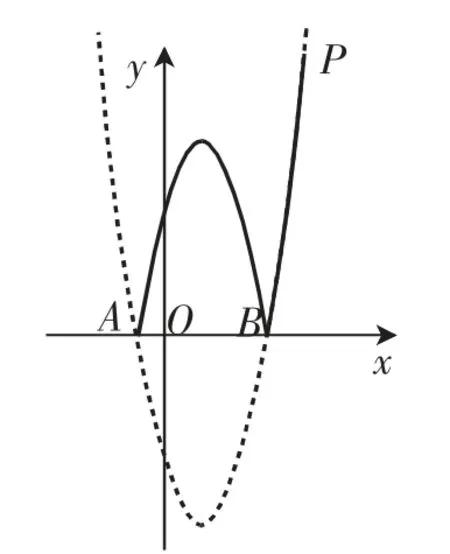
图25

这道题很常规，自然可以用常规解法解决此问题.为呈现惊喜，只反馈学生给出的②的另解：依题意，MN=画出这个函数的大致图像，如图25，图中实线部分反映的就是动点M自点A运动到点E的过程，显然在点P时对应的函数值最大，此时x=5，得MN的最大值为12.

学生积极发言，认真探讨，不断培养学生的能力定在情理之中.学生自己发现的一定是最好的，自己总结完成的一定是记忆深刻的.不仅解决了数学问题，还能变式拓展.

实际上，在教学过程中，为什么强调认真预设？目的就在于能有很好的教学设计，只有充分预设，才能有美好的生成.我们强调过程性，强调学生学习的过程，避免结论性教学直接强加给学生，实际上这就是强化学生活动经验的过程.教育是慢的艺术，所有教师都应在教学设计上精益求精，寻找适当的方法引导学生大胆进行有效探究，在探究中总结共性并积累解决问题的经验，这样抽象的数学思想方法就在潜移默化中掌握运用了.

不去了解学生，不关心学生的诉求，会远离教育的本质.国家发布的中国学生发展核心素养要求，希望处于教学一线的我们能把核心素养和学习质量落实到各科教学中.在教学中回避满堂灌，力求调用多感官运用在学习活动过程中.积极倡导启发式、探究式、讨论式、参与式教学，帮助学生学会学习，发挥学生的创新意识.在我们的课堂教学中能立刻行动起来，改变我们的教育观念和教学方法，让学生“学会、会学、乐学”.倾注一个教育者的爱心、恒心、耐心，在教育过程中，以爱为核心，以情做引线，让学生享受成功的快乐.在我们的教育教学活动中，树立全面发展观念，树立人人成才观念，树立多样化人才观念，树立终身学习观念，树立系统培养观念.深度学习，全面影响每一个学生.做学生成长道路上的关键引路人，一直是我们不懈的追求.