矩形性质的应用价值刍议

江苏省连云港市新坝中学 周洪坦

数学家笛卡儿说：“数学是人类知识活动留下来最具威力的知识工具，是一些现象的根源，数学是不变的，是客观存在的，上帝必以数学法则建造宇宙.”新课程标准指出，学生应学会在具体的情境中发现并提出问题，运用学过的定理、法则与概念解决相关问题，从而提高应用意识与实践能力.矩形是初中阶段研究的重要图形，它具有一些特殊的性质，常与直角三角形、等腰三角形结合考查，在矩形性质的应用过程中，能使我们认识数学的抽象与严谨，体会数学的价值.

一、利用矩形性质求线段的长

矩形是特殊的平行四边形，除了具有平行四边形的一切性质，还具有自己特殊的性质，即四个角都是直角，对角线相等.在矩形中求线段的长有两个途径：一是构造直角三角形利用勾股定理求线段的长，二是利用相似三角形对应边成比例求线段的长.

例1如图1，已知矩形ABCD，AB=，BC=3，在BC上取两点E、F（点E在点F的左边），以EF为边作等边三角形PEF，使顶点P在AD上.

（1）求△PEF的边长；

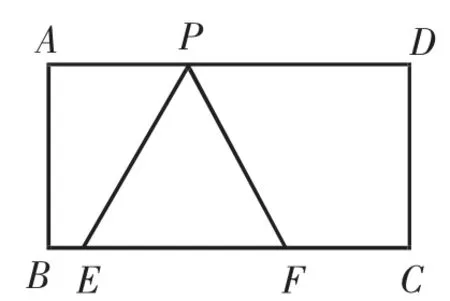
图1

图2

（2）如图2，若△PEF的边EF在线段BC上移动，PE、PF分别交AC于点G、H，求证：PH-BE=1.

解析：（1）如图3，过点P作PQ⊥BC.

图3

由△PEF是等边三角形，得∠PFE=60°，PF=EF=2.

由∠PFE=∠ACB+∠FHC，得∠FHC=30°，则∠ACB=∠FHC，则FC=FH.

由PH+FH=2，BE+EF+FC=3，得PH-BE=1.

评注：本题在求PH与BE的差时，实际上建立了一个方程组，即然后两个方程相减，可得PH-BE=1，较好地体现了方程的思想.

二、利用矩形的性质判定图形的形状

折叠矩形的一个角，使邻边重合，在矩形内得到面积最大的正方形；过矩形对角线的中点画直线交矩形的两边，可得平行四边形；过矩形对角线的中点作垂线可得菱形.在矩形内判定图形的形状，要利用矩形对边平行且相等的性质，要利用四个角都是直角的性质.

例2如图4，在矩形ABCD中，P是AD上一动点，O为BD的中点，连接PO并延长，交BC于点Q.

图4

（1）求证：四边形PBQD是平行四边形.

（2）若AD=6cm，AB=4cm，点P从点A出发，以1cm/s的速度向点D运动（不与点D重合），设点P运动时间为ts，请用含t的代数式表示PD的长，并求出当t为何值时，四边形PBQD是菱形，求出此时菱形的周长.

解析：（1）由四边形ABCD是矩形，得AD∥BC，则∠PDO=∠QBO.

由O为BD的中点，得OB=OD.

（2）依题意得AP=tcm，则PD=（6-t）cm.

当四边形PBQD是菱形时，PB=PD=（6-t）cm.

由四边形ABCD是矩形，得∠A=90°.

在Rt△ABP中，AP2+AB2=BP2，AB=4，则t2+42=（6-t）2，解得，所以运动时间为时，四边形PBQD是菱形.此时菱形的周长为

评注：“t为何值时，四边形PBQD是菱形？”这句话相当于“四边形PBQD是菱形时，求t的值”.在解答时，应从菱形出发，利用菱形的性质求出t的值.

三、利用矩形的性质求角度

因为矩形的四个角都是直角，所以作一个内角的平分线，可得45度的角，可得等腰直角三角形.在已知条件没有角度的问题中求某个角的度数，一般有两种解决办法：一是证明这个角是等边三角形的内角，那么它就是60度；二是证明这个角是等腰直角三角形的一个锐角，那么它就是45度.

例3如图5，在矩形ABCD中，∠BAD的平分线交边BC于点E，交边DC的延长线于点F，以EC、CF为邻边作▱ECFG，M是EF的中点，连接MC.

（1）求证：ME=MC；

（2）求∠BDM的度数.

解析：（1）由AF平分∠BAD，得∠BAF=∠DAF.

由四边形ABCD是平行四边形，得AD∥BC，AB∥CD，则∠DAF=∠CEF，∠BAF=∠CFE，则∠CEF=∠CFE，则CE=CF.又四边形ECFG是平行四边形，则四边形ECFG为菱形.

由四边形ABCD是矩形，得∠ECF=90°，则菱形ECFG为正方形.

由EM=MF，得EM=MC.

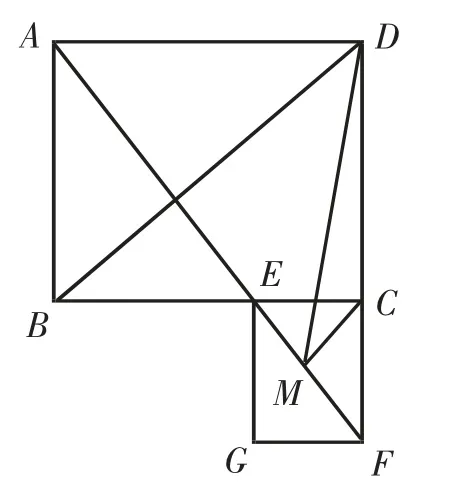
图5

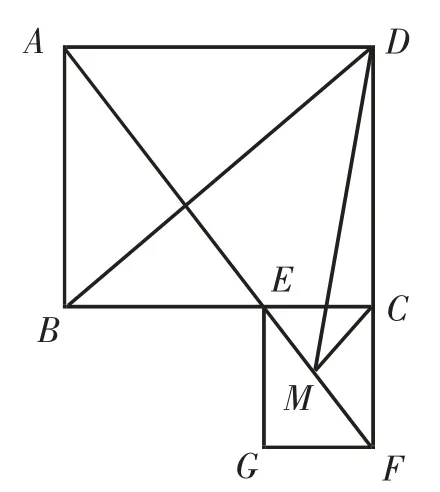
图6

（2）如图6，连接BM.

四边形ECFG为正方形.

由∠BAF=∠DAF，得BE=AB=DC.

由M为EF的中点，得∠CEM=∠ECM=45°，则∠BEM=∠DCM=135°.

∠BMD=∠BME+∠EMD=∠DMC+∠EMD=90°.

则△BMD是等腰直角三角形，则∠BDM=45°.

评注：当角平分线与平行线相遇时，就有等腰三角形出现，主要利用“两直线平行，内错角相等”和“等角对等边”获得证明.如本题“AB∥DF”与“AF平分∠BAD”结合，得到等腰三角形CEF.

四、利用矩形性质解分式方程

矩形的面积等于长乘宽，所以长=面积÷宽，宽=面积÷长.分式方程指分母中含有未知数的方程，所以把分式中的分子作为长方形的面积，分母作为长方形的长或宽时，矩形的要素与分式方程的要素之间就有了对应关系.

例4我们常用“去分母法”将分式方程转化为整式方程，然而古代数学家斐波拉契在《计算数学》中运用“几何代数”法，即运用面积关系将分式方程转化为整式方程，从而求解分式方程的根.请同学们先阅读材料，再解答问题：

解：如图7，AB=10，CB=x，矩形ACGF和矩形CBED的面积均为36，GD=EH=3.于是，整个矩形ABHF的面积为3x+72，故，从而

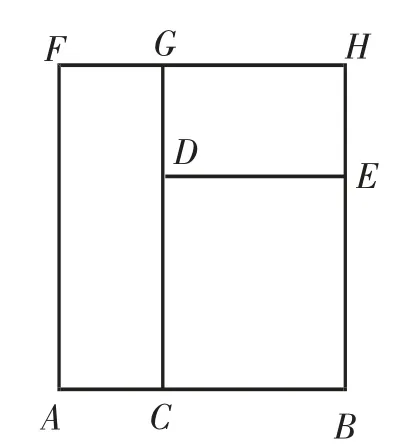
图7

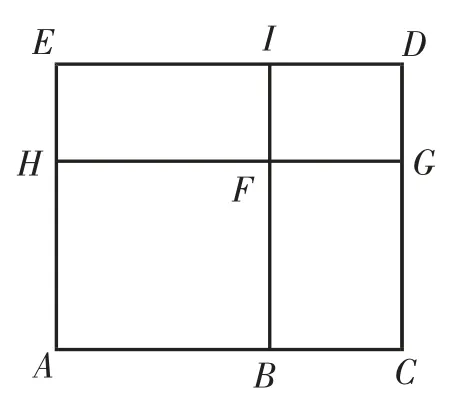
图8

【理解】如图8，AB=x，BC=2，矩形ACDE的面积为60，矩形ABFH的面积为20，FI=5.请根据图形特征完成下列问题：

（2）用“几何代数”法解（1）中的方程.

解析：（1）由题意知

（2）由题意知矩形EHGD的面积=5（x+2），则矩形FBGC的面积=30-5x，从而AH=CG=

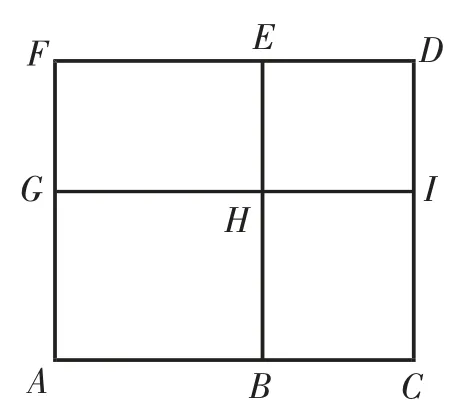
图9

【尝试】构造图形，如图9，AB=x，CA=x+2，矩形ABEF和矩形ACIG的面积均为60，，则BC=2，矩形FGHE与矩形BCIH的面积相等，则则CI=BH=，则矩形ACIG的面积又x＞0，解得x=6.

评注：解分式方程的关键是去分母，将分式方程转化为整式方程.本题通过矩形面积，将分式方程转化为整式方程，体现了分式的几何意义.

教学活动是师生积极参与、交往互动的过程，较好效果的教学活动是学生与教师的统一，学习的主体是学生，教师是学习的组织者、服务者.要让学生体会数学知识之间、数学与其他学科之间的联系，增强学生分析、解决问题的能力.矩形性质的四个应用，体现了矩形与其他知识的联系，通过问题的解决，有效增强了学生解决问题的能力.