从一道中考题说起——谈初中数学数形结合思想展现的魅力

江苏省南京师范大学苏州实验中学 张 璇

在当前的初中数学教学中，学生不仅证明和求解的过程书写混乱，如由“因为”根本推导不出“所以”后面的结论等，而且平面图形的性质无法利用“数”与“形”相结合的思想与方法分析，如二次函数图像的性质等.这就导致大部分初中生将解题思路禁锢于某一个方面，或“代数”方面，或“几何”方面，而不能将二者有效结合起来，从而久久不能将问题有效或高效地解决.数形结合思想便是为了解决这一问题而诞生的新思想、新方法，给初中数学的学习带来了新的希望.

一、提出问题——一道经典的数学中考题

2019年江西数学中考第12题：在平面直角坐标系中，A、B、C三点的坐标分别为（4，0）、（4，4）、（0，4），点P在x轴上，点D在直线AB上，DA=1，CP⊥DP于点P，则点P的坐标为_______.

本题是典型的动点问题，作为填空题的压轴题，文字不多，但对分类讨论思想、数形结合思想的运用都进行了考查，体现了逻辑推理、直观想象的核心素养.由“CP⊥DP”这个条件产生的两种不同情况，预示着后期要采用分类讨论思想.在第二种情况中，如果按照传统做法过程比较复杂，主要会用到“勾股定理”“一元二次方程”等重要知识点.但是，如果能将直角看成两条互相垂直的直线形成的角，即两直线互相垂直，就可以将“几何”问题转化成“代数”问题，这是非常明显的“数形结合”，不仅能帮助学生较快地解出这道题，而且在独辟蹊径之余让学生感受到了数形结合思想的魅力所在.

二、对比分析——感悟数形结合思想的魅力

承上所述，下面对第二种情况的分析过程进行对比，通过对比和分析让学生感悟数形结合思想给学生的学习带来了便利，甚至是“捷径”.

（一）利用常规解题思路进行分析

首先，这样的点D应有两个，一是（4，1），二是（4，-1）.

当点D的坐标是（4，1）时，如图1所示，此时可以设点P的坐标为（m，0），那么OP=m，且AP=4-m.易得到△OCP△APD，因此可列比例式，即OC·AD=AP·OP.将OP=m、AP=4-m代入其中，得到4×1=（4-m）·m，解得m1=m2=2，所以点P的坐标为（2，0）.

当点D的坐标是（4，-1）时，如图2所示，此时可以设点P的坐标为（m，0），那么很容易得到CD2、PC2、PD2的表达式，即CD2=（0-4）2+［4-（-1）］2=41，PC2=（0-m）2+（4-0）2=m2+16，PD2=（4-m）2+（-1-0）2=m2-8m+17.由勾股定理可知CD2=PC2+PD2，继而得到m2+16+m2-8m+17=41，解得m1=.所以，点P的坐标为或

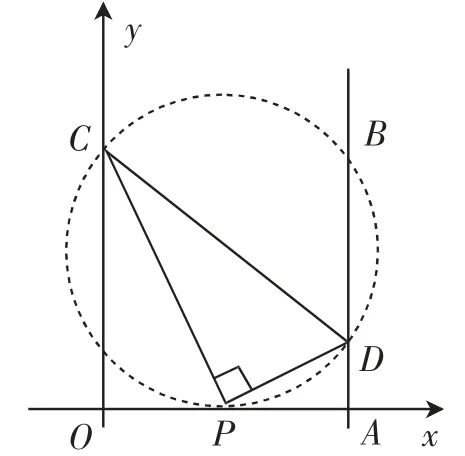
图1

图2

（二）利用两直线的位置关系分析

在几何领域中，两条直线的位置关系有平行和相交两种，其中平行的特例是互相重合，相交的特例是互相垂直.将这一问题放在代数领域中，那么两条直线可以看成两个不同的一次函数的图像.设这两条直线的解析式分别为y=k1x+b1和y=k2x+b2，当k1=k2、b1≠b2时，两条直线互相平行，假如b1=b2，就可以得到两直线互相重合；当k1·k2=-1时，两条直线互相垂直.由此可见，讨论直角的问题不能局限于几何角度，也可以将之拓展至代数角度，即把两条直线看成两个一次函数的图像，然后根据k1·k2=-1得到两条直线互相垂直.所以，对于该题的第（2）问，也可以按照这个思路具体分析，如下所示：

首先，设点P的坐标为（n，0），线段CP所在直线的解析式为yCP=k1x+b1，线段DP所在直线的解析式为yDP=k2x+b2，然后分别将点C（0，4）、P（n，0）、D（4，-1）代入到这两条直线的解析式中，得到.由于CP⊥DP于点P，所以k1·k2=-1，即，解得，最后得到点P的另外两个可能的坐标为

（三）基于两法对比感悟数形结合思想的魅力

通过对比这两种不同的分析方法，不难发现它们都利用到了数形结合思想.第一种方法是将问题分成了两类，然后在分类讨论思想的基础上使用数形结合思想.这种方法比较常规，但是分析的思路比较清晰，因为每分析一类情况就相当于做一个题目，两类情况分析过程彼此独立.但是，计算量比较大，而且容易忽略其中的一种情况.第二种方法并没有进行分类，而是将几何中的直线或线段看成一次函数的图像，然后根据k1·k2=-1得到方程并解出，最后得到点P的另外两个可能的坐标.这种方法灵活性、综合性都比第一种方法更高，特别是完全从代数的角度考虑几何问题，这和第一种方法由几何分析列出代数算式明显不同，也更考验解题人的综合水平.

三、精培巧渗——让学生利用数形结合思想解疑

数形结合思想可以让学生于“穷途末路”处“柳暗花明”，在茅塞顿开之余感受数学的魅力.甚至在掌握这种思想方法后，会因一次次“豁然开朗”而渐渐喜欢上做数学题和慢慢对自己学好数学建立越来越强的自信.所以，作为核心素养理念下的一线初中数学教师，有必要也有义务从以下几个方面培养学生的数形结合思想：

（一）在讲好概念上下功夫

掌握概念是学生学习的重要任务，并且学生需经历形成、理解、应用三个过程.所以，教师在教学数学概念时，要寻找恰当时机向学生渗透数形结合思想.

例如，教师在讲“勾股定理”内容时，就是通过一个直角三角形的三边作出的正方形的面积关系，得到这个直角三角形三边的关系，而这种关系就是勾股定理的内容.勾股定理可以用一个表达式概括，而其推导过程就是建立在几何层面上，将“数”与“形”进行了有效结合，向学生渗透了数形结合思想.

再如，教师在讲到“二次函数的图像”时，就是利用数与图形相结合的方式为学生展现了二次函数的开口及开口方向、对称轴、顶点，从而让学生对二次函数的三要素有更清晰的了解.特别是利用图形分析二次函数的增减性时，往往是在一幅二次函数图像上分别取几个不同的点，然后通过比较相对应的y值及其在坐标平面上的高低、正负，便得到了二次函数的增减性.这样一来，原本非常抽象的内容在利用数形结合思想之后，问题和分析过程变得更直观、更简单.

（二）在问题解决时潜移默化

常见的可用数形结合思想解决的数学问题主要有两大类，一类是代数问题用几何的方法解决，另一类是几何问题用代数的方法解决，其中解直角三角形、函数等问题比较多见.

例如，有这样一道中考数学题——一次函数y=kx+k的图像过点（1，4），且分别与x轴、y轴交于点A、B.点P（a，0）在x轴的正半轴上运动，点Q（0，b）在y轴的正半轴上运动，且PQ=AB.

（1）求k的值，并在直角坐标系中画出该一次函数的图像；

（2）求a与b满足的等量关系式；

（3）若PQ⊥AB，求a、b的值.

本题对学生掌握分类讨论思想、数形结合思想的情况进行了考查，重点在于学生应用知识推理出正确的结果.通过图像或画图解决一些函数问题，是当前中考中炙手可热的命题类型.将函数图像特征、代数数量关系等结合起来，能有效帮助学生解决问题、检验问题解决的结果.

四、结语

总之，面对很多学生无法在“代数”与“几何”间灵活转换，从而不能很好地利用数形结合思想解决问题的不足，一线初中数学教师一方面要正视，另一方面要积极在日常教学中渗透数形结合思想，让学生领略它的魅力.