浅析中考“四步三点”总复习策略

江苏省如东县洋口镇初级中学 顾晓云

数学的总体复习工作是初中阶段全面知识点教学结束之后系统、全面、融会贯通掌握学到的知识点的重要一步.总复习的时间不长，但牵扯到多个知识点，想要在不长的时间里收获不菲的复习效果，实现提高学生的教学水平的目标，就需要在总复习之初就教给学生正确的复习方式.对近几年的数学中考情况进行汇总比对，考虑到目前数学总复习的情况，提出以下几点复习建议.

一、钻研《考纲》，回归教材

想要达到好的复习效果，必须正视课程标准的重要性，它不仅是教学的指导方向，也是考试的命题范围，只是课程标准的要求是有一定弹性的，所以说教学的重心就是要将《考纲》内容吃透，按照课程标准给学生指出考点、重点，并且对考点涉及的知识点做好汇总归类工作，将知识点彼此间的关系、区别罗列在一起，形成知识网.

二、因材施教，分类指导

中考前的总复习环节，教师必须考虑到学生掌握的知识点有多有少，在设计复习内容时既要考虑到学生的整体水平，又要兼顾不同水平的学生，最终使得每个学生的数学水平都能提升.所以，教师需要将学生按照数学水平的高低进行简单分类，为不同层次的学生设定的教学目标是不同的，自然复习模式、课后练习等都是有差异的.对于课后练习的内容，基础薄弱的学生可增加基础内容的练习，而中等水平的学生可以在基础内容之上，做些巩固提高的练习，数学水平优异的学生则可以做些难度高、综合性强的题目，并且教师要根据学生反馈的教学效果灵活设定学生课后练习的难度和数量.每个学生都有自己擅长的部分，如空间想象能力好的学生对于“图形与几何”部分掌握得要更好一些；运算能力强的学生对“数与代数”部分掌握得更熟练；而实际应用能力强的学生对“统计与概率”更能应用自如.因此，教师可以让学生依照自身基础状况进行练习，这样学生不会因基础薄弱而丧失学数学的积极性，还能真正了解自己的不足.如复习中考中重要考点全等三角形时，教师可以将课后练习题按照是否作辅助线分为两类，难度逐层递进，让学生练习.

（1）不需作辅助线的全等练习.

已知BD⊥AC于点D，CE⊥AB于点E，AD=AE.求证：BE=CD.

证明：由BD⊥AC于点D，CE⊥AB于点E，得∠ADB=∠AEC=90°.

（2）需作辅助线的全等练习.

已知△ABC是等腰直角三角形，∠BAC=90°，BD平分∠ABC，CE垂直于BD，求证：BD=2CE.

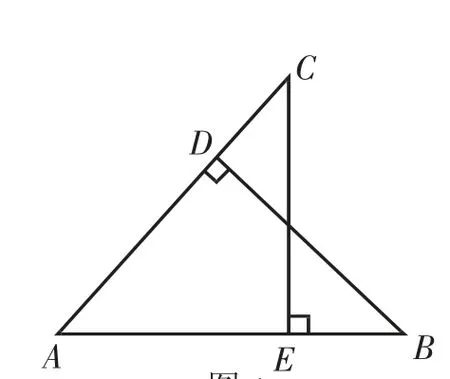
图1

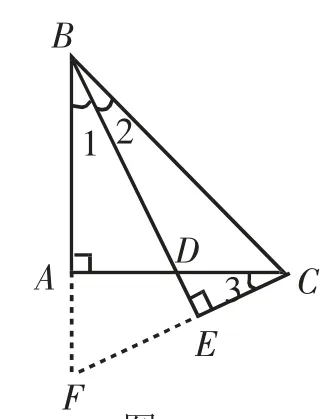
图2

证明：延长BA、CE交于点F.

在△BEF和△BEC中，∠1=∠2，BE=BE，∠BEF=∠BEC=90°，则，则EF=EC，则CF=2CE.在△ABD和△ACF中，∠1=∠3，AB=AC，∠BAD=∠CAF=90°，则则BD=CF，则BD=2CE.

三、重视方法，巩固知识

我们教学的目标是学生能够拥有学习知识的手段，并且能够主动学习知识，拥有开创意识和能力.中考数学总复习并非一件简单的事情，短时间内将初中三年的知识点进行梳理，让学生能够巩固提升数学水平，这些仅靠课堂教学是无法完全实现的，想要在短时间内提升学生的数学水平，必须让学生主动学习，主动思考自己数学学习中的薄弱地方，哪些知识点掌握得不稳固，哪些知识点没有掌握等.学生每隔一段时间都要温习自己的笔记和试卷，看到错题时看一下是什么知识点，掌握熟悉的知识点，这样才能达到巩固知识的目的.所以说，学生最好能将自己做错的题目进行汇总，找到自己出错的根源，避免以后再犯同样的错误.

四、把握命题方向，要抓好“点”的复习

这几年中考数学题目年年都会有变化，而复习的时候要牢牢抓住以下几个方面：

1.狠抓重点、难点

将主要精力放在重、难知识点的学习上，掌握并巩固所学到的重、难知识点.学习时，就是要在全面复习的基础上，将教材中的重、难知识点拿出来讨论，重点掌握.通读是为了对于知识点有一个全面的梳理，精读是掌握知识点的关键，是将重、难点吃透的过程.这些年中考的综合题多是将知识点、技能等进行汇总，所以说重点知识的复习不仅要掌握知识点，还要获得自主学习的能力.每个题目的学习都要了解到自己对知识点的掌握情况，学习知识的同时掌握学习的能力，抓重点的同时，还要全面掌握所需的知识点.对于历年经常出题的知识点，作为重、难点，专题复习.

2.精抓易错点

对于经典题型，不仅要让学生明白题目涉及的知识点有哪些，还要知道测试的知识点是从哪方面测试的，解题时应该从哪方面入手，解决方式有几种，哪种解题方式最佳.倘若解题错误，要弄清是审题错误导致运用的知识点错误，是自己对知识点掌握不牢靠导致使用的方法错误，还是解题时粗心大意导致错误等.以全等三角形为例，学生一定要熟知判定方法共有几种，还有就是哪些方法不能作为判定方法.

△ABC中，AB=AC，D、E分别为AB、AC的中点，CD=BE，证明

错误答案：AB=AC，BE=CD，∠BAE=∠CAD，则△ADC△AEB（SSA）.

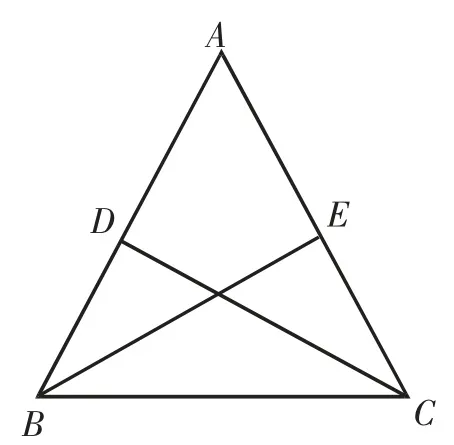
图3

分析：SSA不能作为判定全等的条件，因两边及一边的对角相等的三角形不一定全等.

证明：由AB=AC，D、E分别为AB、AC的中点，得AD=AE.

在△ADC和△AEB中，AB=AC，AD=AE，CE=BE，则

只有了解自己的错误到底是哪种原因导致的，才能避免下次遇到同类型的题目时出现类似的错误.

3.巧抓热点

分析历年的中考数学试卷，将其中的典型题目作为例题，根据中考的特征挑选以下题型.（1）应用型问题.应用类的题目在近些年的考试中是热点，题型也较为多样.社会、经济、环保等热点问题都曾出现在历年考题中.（2）图表类题型.（3）测试学生自学水平的阅读题型.（4）测试学生应变水平的开放类题目.（5）测试学生创新水平的归纳猜想题型.

在中考复习中，必须将课程标准作为基础，教师要协调好课上和课下，教材和辅导，重、难知识和普通知识的关系，而且要对学生的三个方面保持关注度：关注学生学习的参与程度，是被动学习还是主动学习；关注学生的思维方式，学生能否跟上教学进度，学生敢不敢提问，提问是否具有创新性；关注学生的学习情绪，是否松紧有度，对学习是否充满信心.教师只有尽可能提高学生学习的积极性，为学生营造良好的复习氛围，才可能达到好的复习效果.F