由数形结合解读几何课堂教学——从矩形的判断课例说起

浙江省天台县外国语学校 林炳江

上学期期中考试刚刚结束，学校就全面铺开了每一学期的教研活动.这次教研活动以“示范课”为引领活动核心，以学科组集体备课和课后反思为活动抓手，让学校工作以教学为首位，以学生为基本，沉浸到了教研的氛围之中.为了在课堂上做好示范引领作用，在学科组集体备课的基础上，笔者勇挑“讲课”的重担；在课后又进行了学科组的交流.笔者作为主讲教师感悟至深，课余之时将这些灵感流于笔端.

一、学科组集体备课让笔者对课堂内容有了更深刻的认知

本次教研活动所选内容“矩形的判断”是第8册下的内容，但因为中招的需要，学校要求将课程前移，在本学期提前结束第8册下的内容.为了在缩短教学进程中使课堂高效，学科组集体备课是课堂教学的教研活动的前奏.

在学科组集体备课时，笔者首先提出了自己对教学目标、教学重点、教学难点的理解，由学科组成员一起研讨，在其他学科组成员的交流和改进中进一步整合，让这部分内容能够在课堂上驾驭得“游刃有余”，让学科教师能够在学校教研活动中“脱颖而出”.在许多磨合中让笔者感受至深的有这样两点：第一，笔者认为课堂教学的目标就是使学生能应用矩形定义、判定等知识，而有学科组成员提出不但明确“判定”知识，在课堂上学生还应该能利用知识去完整地完成简单的证明题和计算题，这是培养学生分析能力的关键所在；第二，笔者认为要通过矩形判定来灌输“数形结合”的数学思想，而学科组成员又提到将矛盾能够互相转化的辩证思想贯穿在教学之中.

在集体备课时，笔者认为教学重点和难点都是矩形的判定，这是教学核心内容，但有些学科组成员则补充了“矩形的判定及性质的综合应用”.还有就是对例题和课堂练习等的设计，这块内容可以在课堂教学中具体说明，在这里就不一一细说了.总之，通过备考交流，自己的思维活跃了起来，有了上好课的信心.

二、学科组参与指导让笔者对课堂教学有了全新的诠释

在集体备课时，与学科组成员达成共识，本节课采用“观察、启发、总结、提高”的方法对内容进行展开与拓展.

1.导入新课

在电子白板上展示三个问题（让学生思考旧知）：

（1）叙述平行四边形和矩形的定义.

（2）你能说出矩形有哪些性质吗？

（3）比较矩形与平行四边形，谈谈二者有什么共同之处，有什么不同之处.

教师巡查，观察学生思考的情况，然后通过三个学生对问题的回答做出点评，并导入新课——矩形的判定.

设计目的：让学生回顾已有的知识，以平行四边形和矩形的定义作为起点，在回答问题的过程中组织教学，从而达到“温故而知新”的目的.

2.讲授新知

拿出一个四边形模具（有两种形式的模型，如图1）进行演示，然后学生通过小组合作进行观察、探究.

图1

学科组成员帮助分发平行四边形模具给各小组，并参与小组的讨论.

让小组推荐成员谈谈在探究过程中发现的规律（中等学生）：将平行四边形的一个锐角增大，变成90°（用直角三角板靠上去），再测量其他几个角得到都是90°.若是任意四边形，将四边形的一个锐角增大，变成90°（用直角三角板靠上去），再测量其他几个角，不一定是90°.

设计目的：学生在总结规律时用模型来说明，体现了动手能力，在其他老师的指导下，让课堂氛围变得自然、和谐，同时学生受到启迪后，描述发现的规律也自然、得体.

小结新知：在电子白板上展示：

有一个角是直角的平行四边形是矩形.

拓展说明：有一个角是直角的平行四边是矩形，因此，判定一个四边形是不是矩形，必须确定它是不是平行四边形，然后观察它有没有角是直角.用“定义”作为判定是最重要和最基本的数学思维方法.在任何科学的定义面前，定义必定体现性质和判定的双重作用.让学生明确，准确掌握数学“定义”是非常重要的.

在解释定义之后，学生继续推理，有学生得出了“有三个角是直角的四边形是矩形”的结论.让学生在纸上写出推理过程，然后进行投影并讲解.

提出第2个判定定理：对角线相等的平行四边形是矩形.

活动过程同第1个判定定理类似，先分析判定方法，再让学生自主完成证明过程，并抽出几个学生进行展示、对比.

设计目的：让学生动手后进行反思，让在探究中发现的规律潜移默化为数学思维能力.几何推理逻辑性强，需要“步步为营”，不能缺少中间的任何环节.在课堂上学科组教师的参与让这种逻辑性变成学生的推理准则成为可能，因为教师的督导让学生集中了精力.

学生归纳：上面讲到的矩形判定方法有三种：

（1）有一个角是直角的平行四边形是矩形；

（2）对角线相等的平行四边形是矩形；

（3）有三个角是直角的四边形是矩形.

3.例题示范

用电子白板展示例题，让学生思考，然后师生共同完成.

例题：如图2，已知▱XYZW的对角线XZ、YW相交于点O，△XYO是边长为3cm的等边三角形，计算该平行四边形的面积.

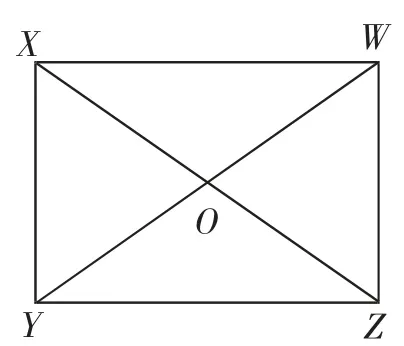
图2

释疑过程：第一步，让学生将学习的新知识进行运用：判断▱XYZW为矩形；

第二步，计算特殊直角三角形XYZ的边YZ的长（有一个角为60°的直角三角形，两个直角边存在怎样的关系，这是数形结合思想）；

第三步，计算矩形的面积（基本公式）.

学生自主写出步骤，然后将结果通过投影展示、教师点评并进一步深化.

设计目的：本题是根据“对角线相等的平行四边形是矩形”确定▱XYZW是矩形的，这要求学生具有平行四边形是对称图形的理解能力，让学生在推理过程中能将数代入进行运算，这是对他们的“数形结合”数学学科核心素养的提升.

补充例题：判断下列命题的正确性.

（1）若一个四边形的两条对角线相等，则这个四边形是矩形.（ ）

（2）若一个四边形两条对角线相等且互相平分，则这个四边形是矩形.（ ）

（3）若一个四边形有一个角是直角，则这个四边形是矩形.（ ）

（4）在一个矩形内部可以找到一个与四个顶点距离相等的点.（ ）

具体分析略.

4.课堂小结

再次强调并提升知识.

要求学生在矩形的判定方法中厘清判定的两个条件：①是平行四边形，②有一个角是直角或对角线相等（是数形结合）；或是：①是四边形，②有三个直角（是数形结合）.

设计目的：用补充例题来巩固学生对新知的理解，尤其是通过一些命题的判断，让学生有“幡然醒悟”的辨别能力，并通过学生的深入认知进行课堂小结，这样就能起到举一反三、事半功倍的效果.同时学科组其他教师参与检查督导，让学生量力而行，让所有的学生都有收获.

三、学科组点评形成了教后反思与提升

学科组成员参与课堂活动之后，投给笔者以赞赏的目光，说明笔者的课堂活动是成功的.同时提出了很多宝贵的建议.比如，能否缩短旧知复习的提问时间；能否将“对角线相等的平行四边形是矩形”的证明过程让学生自己去展开而不是教师强化；能否在例题之后再做几道变式练习，让学生通过小组对抗赛的形式来激发课堂热情……

是的，毕竟作为一节教研类型的课，有许多不足之处是必然的，学科组教师给了莫大的肯定和点赞，让我在教学生涯中有了前进的动力.我知道，唯有在教研活动中去大浪淘沙，才能获得拾起属于自己的那块金子的机遇.