北京市通州区电动汽车充电电量需求分析

段晨悦

(北京物资学院 经济学院,北京 101149)

1 引 言

电动汽车的发展离不开其充电基础设施,只有不断完善充电基础设施的建设,才能加快汽车用户选择电动汽车作为代步工具的步伐。英法德等多国已宣布未来将全面停售传统燃油汽车,电动汽车必将逐步替代传统燃油汽车,成为主流代步工具。我国现阶段充电基础设施尚未完全覆盖,而区域单日充电电量可以在一定程度上反映充电基础设施的建设情况,通州区作为北京市“城市副中心”,其单日电动汽车充电电量具有一定的代表性,对其进行研究分析对推动我国电动汽车的发展有着至关重要的意义。

目前,国内关于电动汽车充电电量需求分析的研究较少。许文超等(2011)研究了江苏省充电站的需求,并构建了充电站需求预测模型,主要考虑区域内电动汽车保有量、单次充电平均续驶里程、每公里耗电量、平均充电时间、充电次数等因素。[1]刘文霞等(2012)研究了一地区快速充电站的需求,考虑了快速充电的日需求总量、电动汽车类型、各类电动汽车保有量、各类电动汽车平均百公里耗电量、各类电动汽车日平均行驶里程等因素。[2]武中(2017)研究了不同种类电动汽车对充电设施规划的影响,将电动汽车分为电动私家车、电动出租车、电动公交车、电动公务车,根据其行车特性构建设施规划模型,考虑了续航里程、平均日行驶里程、各区域(居住区、工作区、商业区、公共服务区)停车充电比例及次数等因素。[3]这些研究对我国不同地区充电设施的需求及部分充电电量进行了一定的研究,对未来充电规划具有指导意义,但未考虑充电电量自身增长情况。

国外关于电动汽车充电电量需求有部分研究,N.Andrenacci等(2016)研究了罗马的充电基础设施优化配置的策略,以电动汽车代替传统燃油汽车来构建区域的能源需求,优化设施分配建设问题。[4]Mariz B.Arias等(2017)研究了韩国首尔市区内公共快速充电站的电动汽车充电需求,构建马尔科夫链交通模型,利用远程传输方法确定电动汽车到达率,并构建早晨、下午、晚上三个时间段的时间空间充电需求模型。[5]HyungBin Moon等(2018)基于电动汽车用户偏好、充电时间、电动汽车供电设备的种类,研究了消费者充电需求的变化,发现消费者进行充电行为时会在完全充电时间和充电价格之间进行权衡。[6]Guus Berkelmans等(2018)研究了阿姆斯特丹的充电需求,并构建了交叉嵌套的回归模型进行预测。[7]这些研究涉及国外部分地区的充电电量需求研究,偏向于规模化研究,缺少对单日需求的影响因素的研究。

国内外关于电动汽车充电需求的研究主要集中在电动汽车充电基础设施建设的产业政策、充电基础设施的布局选址、充电基础设施的营运模式等方面,区域单日充电电量需求分析的研究尚不完全,例如：仅将充电电量作为基础设施研究的影响变量。文章与其他研究不同的是考虑了天气因素、出行日类别,以及电动汽车充电电量自身的Gompertz增长,构建通州区电动汽车单日充电电量的预测模型。

2 充电电量需求模型

截至2017年10月31日,北京市通州区已建成53座电动汽车充电站,交、直流充电桩939台。

电动汽车充电电量局部存在波动,但整体呈现上升趋势。电动汽车充电电量的需求处于上升阶段。

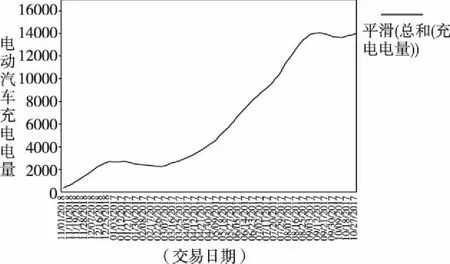
图1 2016年11月至2017年10月北京市通州区电动汽车充电电量

2.1 充电电量增长趋势

电动汽车作为新兴产品,考虑产品生命周期,已进入成长期,其需求呈现增长。而电动汽车充电电量依附于电动汽车的增长,结合图1,将充电电量的增长趋势看作符合Gompertz增长的趋势。

Gompertz增长率公式为：

(1)

Gompertz增长模型公式为：

logω=logα+(-βe-kt)

(2)

ω=αexp{-βe-kt}

(3)

其中ω为总充电电量(每日、周、月),t为日、周、月。

令e-kt为GMt变量,即充电电量增长影响因素。

2.2 总需求模型

2.2.1 单日充电电量影响因素

影响单日充电电量的因素是多方面的,其中出行日的类别、天气状况、电动汽车保有量、充电电量增长情况是最为重要的影响因素,具体包括：工作日、周末、节假日、最高气温、最低气温、风力分级、天气情况、保有量等。这些因素对单日充电电量的影响强度在后续模型中会得到验证。

将日期分为工作日、周末、节假日；风力分级,5～6级或大于6级的风为强风,3～4级或4～5级的风为中风,小于等于3级的风为弱风；天气情况,小雪、中雪、大雪、小雨、中雨、大雨、雷阵雨等为雨雪天气,晴、多云、阴为温和天气,霾为污染天气。具体影响因素见表1。

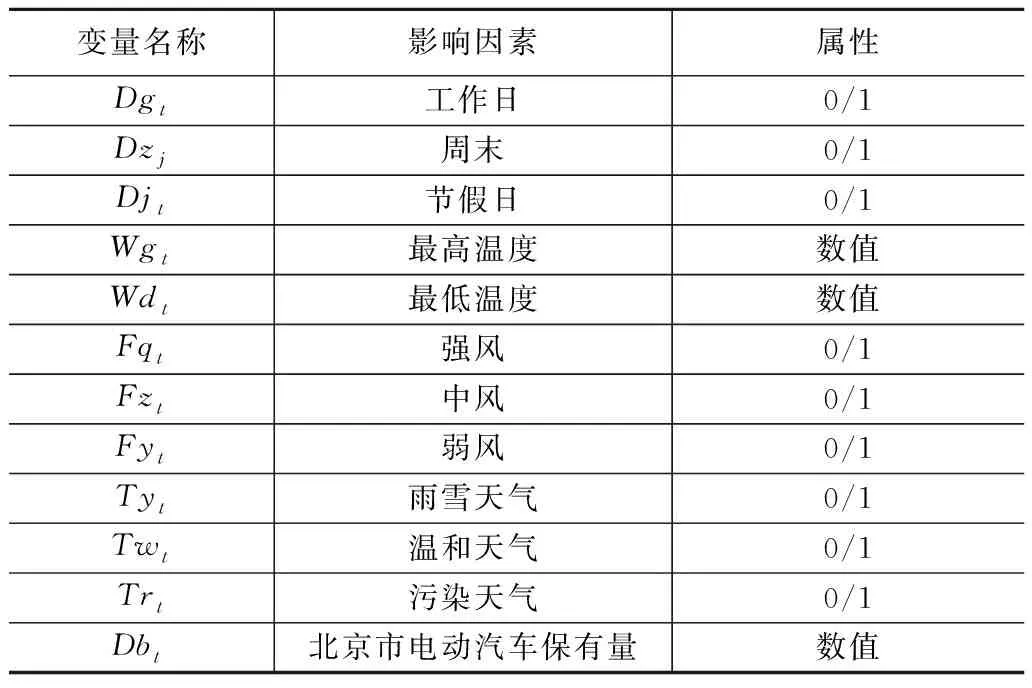
表1 影响因素

2.2.2 总需求模型

单日充电电量需求,不仅依赖于其自身的增长趋势,还依赖于其他影响因素。将充电电量自身的Gompertz增长嵌入需求模型中,构建总需求模型,即：

logωt=α+β0×e-kt+β1×Dgt+β2×Dzt+…+β12×Dbt

(4)

3 模型估计

3.1 增长趋势中参数K估计

Smith等介绍了Gompertz增长模型及其估算过程[8],模型形式如下

(5)

其中ωt为在时间t的充电电量。式描述了充电电量随时间的增长模式。通过构造日、周、月,三个时间的充电总电量,利用式,估算k值。

由表2可知,当k=0.4时,模型拟合程度最优。综上所述,在总需求模型中,取k=0.4。

由k1,k2,k3的取值,估算k的取值范围,可能是0～0.5。通过拟合总需求模型,确定最终的k值。

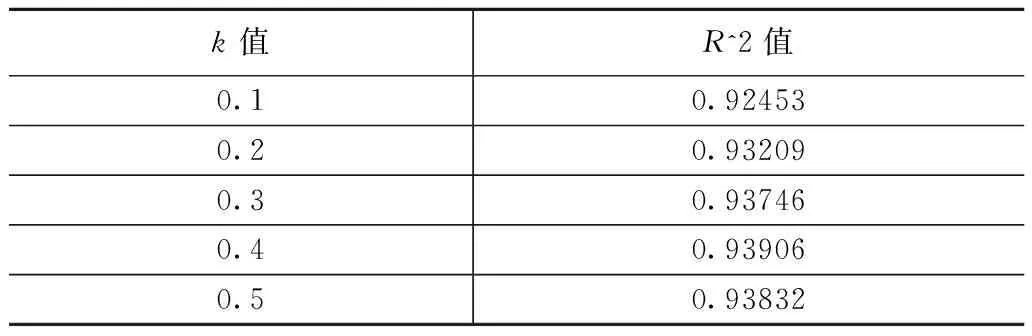
表2 k值与R^2

3.2 总需求模型估计

电动汽车单日充电电量主要受充电交易相关数据、天气数据、电动汽车保有量数据等的影响,以上数据只能通过日期进行关联从而构建模型,同时保有量数据无法精确到单日,如何进行较为准确的估计依赖于调整的方法选择。其中对电动汽车充电电量的预测,选择构建成熟的回归模型；并对通过调查收集的数据进行整理,得到具有完整性、统一性、真实性、标准化的结构数据。

在总需求模型中,提到13个影响因素,其中电动汽车保有量数据,以全国年末保有量数据以及全国每月电动汽车销售数据为基础,以上一年底保有量加前n个月销售量得n+1月的电动汽车保有量。举例说明,2017年1月电动汽车保有量以2016年12月底电动汽车保有量替代,2017年2月电动汽车保有量以2016年底电动汽车保有量加2017年1月电动汽车销售额替代。北京市电动汽车约占全国电动汽车的百分比为P,则对得到的全国电动汽车月度保有量乘以P,作为北京市电动汽车月度保有量数据。以上处理存在部分偏差,但具有一定的代表性。

对总需求模型中各影响因素进行估计。

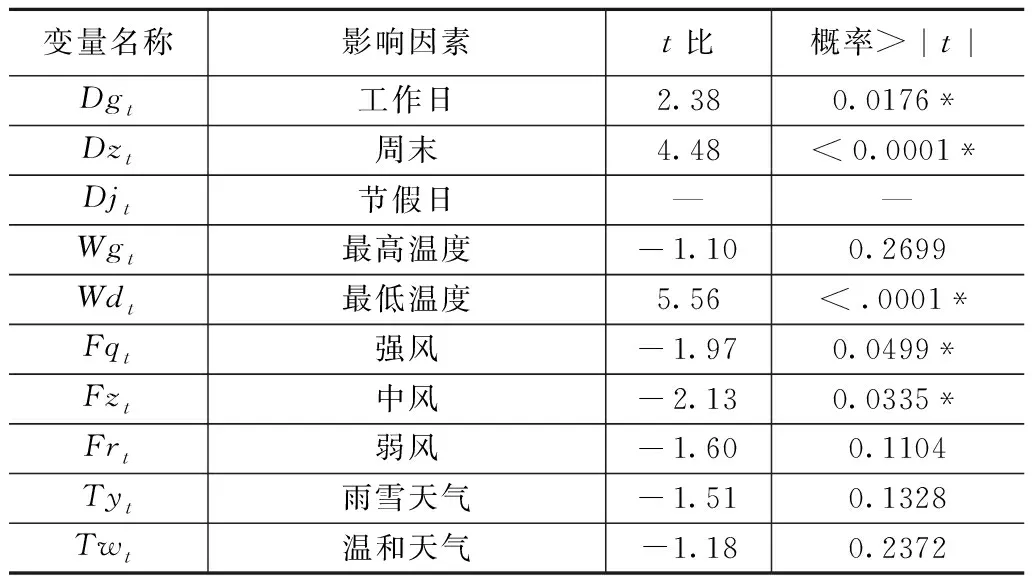
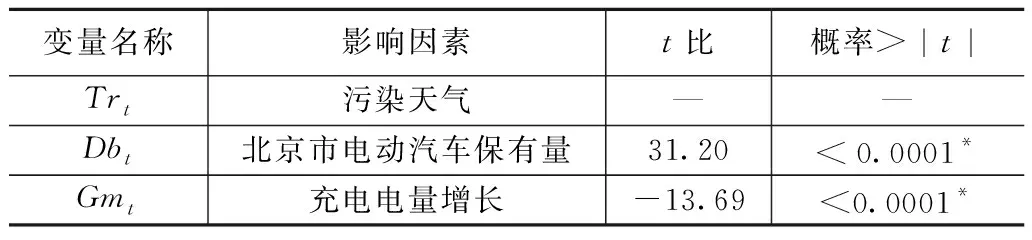
表3 变量t-检验

续表

通过t-检验剔除节假日、最高温度、强风、中风、弱风、雨雪天气、温和天气、污染天气8个影响因素，见表3。

对挑选出的影响因素进行深度分析,构建对数多元回归预测模型,得出各影响因素的影响强度,具体情况见表4。

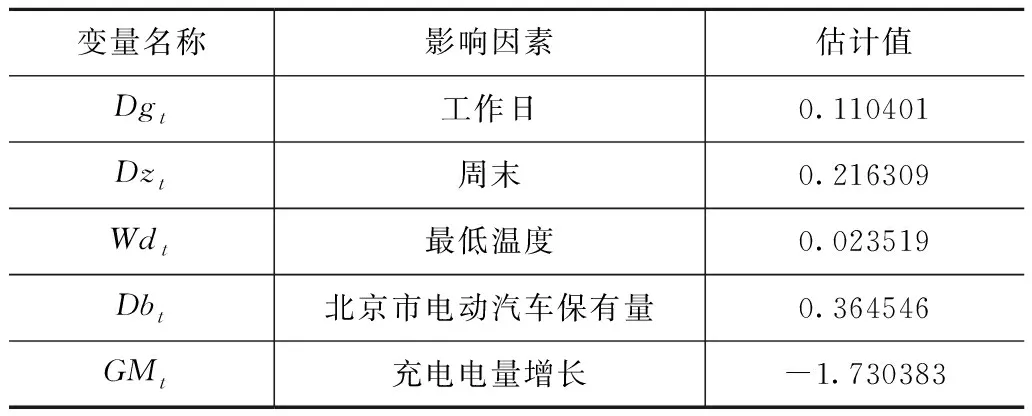
表4 参数估计值

综上所述,对数回归模型为：

logωt=4.910+0.110Dgt+0.216Dzt+0.02Wdt+0.365Dbt-1.730GMt

(5)

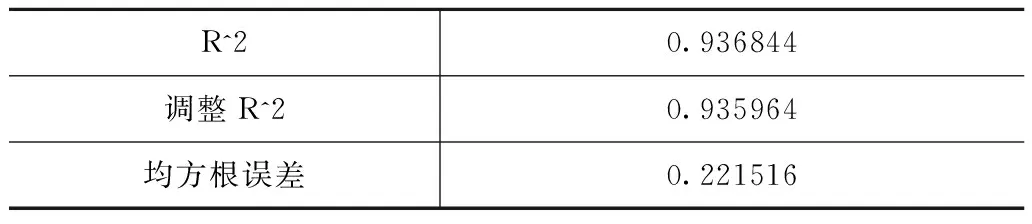
通过表5可知,模型拟合程度较好。根据上述模型,可以发现工作日、周末、最低气温以及北京市电动汽车保有量、充电电量增长这些因素对于单日充电电量的影响最为显著。相对于节假日来说,工作日、周末电动汽车充电均较多,而周末充电多于工作日；最低温度越高,电动汽车充电电量越多；北京市电动汽车保有量越多,电动汽车单日充电电量越多；充电电量随着时间推移,呈现增长趋势。

4 电动汽车充电电量预测

以下分析基于2016年11月1日至2017年10月31日的北京市通州区电动汽车充电交易数据、天气数据以及电动汽车保有量数据等,经过对数据的初步处理,构建多元对数回归模型,即式(5)。

为了更清晰地观测预测结果,以2017年11月1日至2017年11月15日数据作为检验数据,获得预测值和实际值的曲线图。

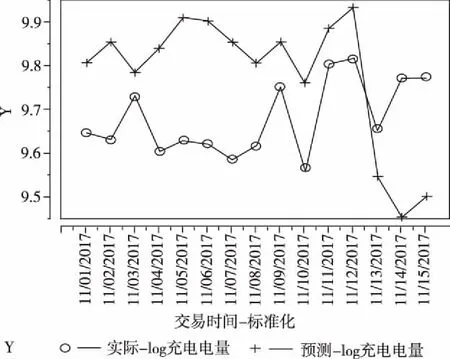
图2 北京市通州区充电电量预测结果

由图2可知,预测结果与实际结果波动几乎一致,但部分存在偏差,预测的log充电电量与实际的log充电电量的误差绝对值最大为0.31,误差均值为0.19。解释说明,因本月保有量以上一月度月末保有量替代,而本月中后期的实际保有量与上一月度月末保有量的差距是随时间递进逐渐变

大的,导致每月中后期预测的充电电量与实际的充电电量的偏差。综上所述,预测整体效果较好。

5 结 论

通过对北京市通州区充电交易数据、天气数据、电动汽车保有量数据的整理,借助对数多元回归模型等方法,充分了解了通州区的充电电量需求。文章的研究对于通州区未来电动汽车充电基础设施的管理、建设具有一定的实际意义和应用价值,随着充电网络系统的不断完善及统计方法的不断改进,还有更多的问题值得我们去探讨。