超短基线定位系统在沉管测控中的应用

赵心1，喻敏，丁贤君

(1.中国船舶工业系统工程研究院,北京 100036;2.武汉理工大学 交通学院,武汉 430063)

随着水上交通的发展，单一的沉管定位方法已经很难满足施工的需求，随着沉管的施工环境向远岸、深水发展,将多种定位方法[1-2]进行组合，集合成综合定位系统已成为现代沉管隧道沉放定位技术的主流[3-4]。其中，将水声定位技术与广域差分GPS定位技术相结合，可获取沉管的大地坐标，且受环境因素影响较小，无需安装测量塔，已成为解决深水沉管隧道管节沉放的有效途径。

提出将沉管沉放定位分为两个阶段：粗测阶段及精测阶段。在粗测阶段，将超短基线(USBL)声学定位系统与GPS组合，对下沉阶段的管节位姿进行实时测量，引导待沉管节沉放至预定位置，省去测量塔的安装，提高施工深度；在精测阶段，由精测定位系统(如超声波定位[5]，机械定位[6])完成沉管最终对接。本文重点围绕粗测阶段，详细给出基于水声定位系统和GPS定位系统的沉管定位方案。

1 沉管定位方案

1.1 方案布置

针对待沉管道下沉施工阶段，提出基于超短基线定位系统对待沉管节姿态进行实时测控。安装在施工平台(如驳船)舷侧的超短基线系统以声波作为载体，对固定在待沉管节表面的应答器进行定位。驳船上安装有GPS天线以及姿态传感器，用于将超短基线坐标系下的定位信息转换到大地坐标中。因此，需要建立3个坐标系：以GPS天线为原点的大地坐标系、以驳船重心为原点的船心坐标系和以超短基线基阵中心为原点的基阵坐标系，通过姿态传感器测量的船姿态信息及GPS天线的大地坐标，根据欧拉旋转矩阵对3个坐标系进行转换，最终可获取待沉沉管在大地坐标系中的位姿信息。见图1。

图1 基于USBL定位系统的沉管定位方案

从管节下沉开始，位于沉管上表面的应答器便不间断地发射预置脉冲信号，基阵持续接收脉冲信号。超短基线系统根据基阵阵元间的相位差解算出应答器在基阵坐标系中的位置，并通过位姿解算方法获得沉管的位姿信息。然后通过坐标转换获取沉管在大地坐标系中的绝对位姿信息。最终，显示器实时显示沉管在大地坐标系中的三维位姿，对现场施工进行连续监控。

1.2 位姿解算

已知应答器安装在待沉管节上，且待沉管节上的应答器在一个平面上，即可根据三点共面条件，通过求解应答器坐标获取待沉管节平面上的3个点，继而求出待沉管节平面在基阵坐标系中的姿态信息。

设待沉管节平面的平面方程为

Ax+By+Cz=1

(1)

式中A、B、C为未知参数，至少需要3个不共线的坐标，可解出A、B、C。之后，可通过平面的法线式方程得到待沉管节平面在基阵坐标系中的法向矢量，即待沉管节平面的方向余弦向量。

(2)

(3)

设USBL基阵所在的平面为XOY，则基阵平面的法向量就可表示为IU=[0,0,1]′，则从管节平面法向量到USBL基阵平面法向量的旋转矩阵可表示为

(4)

设从USBL平面到待沉管节平面的绕基阵坐标轴旋转的欧拉角为θx、θy、θz，则R是关于θx、θy、θz的旋转矩阵，根据旋转矩阵R即可以求出待沉管节平面的姿态角度。

1.3 多址定位技术

由位姿解算方法可知，对沉管定位过程中需要对多个应答器(≥3)进行定位，因此涉及水下多址定位技术，即每个应答器通过发射不同形式的脉冲信号，超短基线系统根据接收到的脉冲信号来分辨不同的应答器，并确定每个应答器在基阵坐标系下的坐标。由于自身具有调节参数的能力以及对信号和噪声的先验知识要求少，且在高信噪比下，Notch滤波器有着良好的相位差估计能力，可以作为超短基线系统多址信号检测器及相位差估计器。

首先根据应答器的个数来设计可用带宽，Notch的每路参考信号的频率分别对应应答器的中心频率。假设需要安装3个应答器，则其对应的3路并联Notch滤波器的结构图见图2。

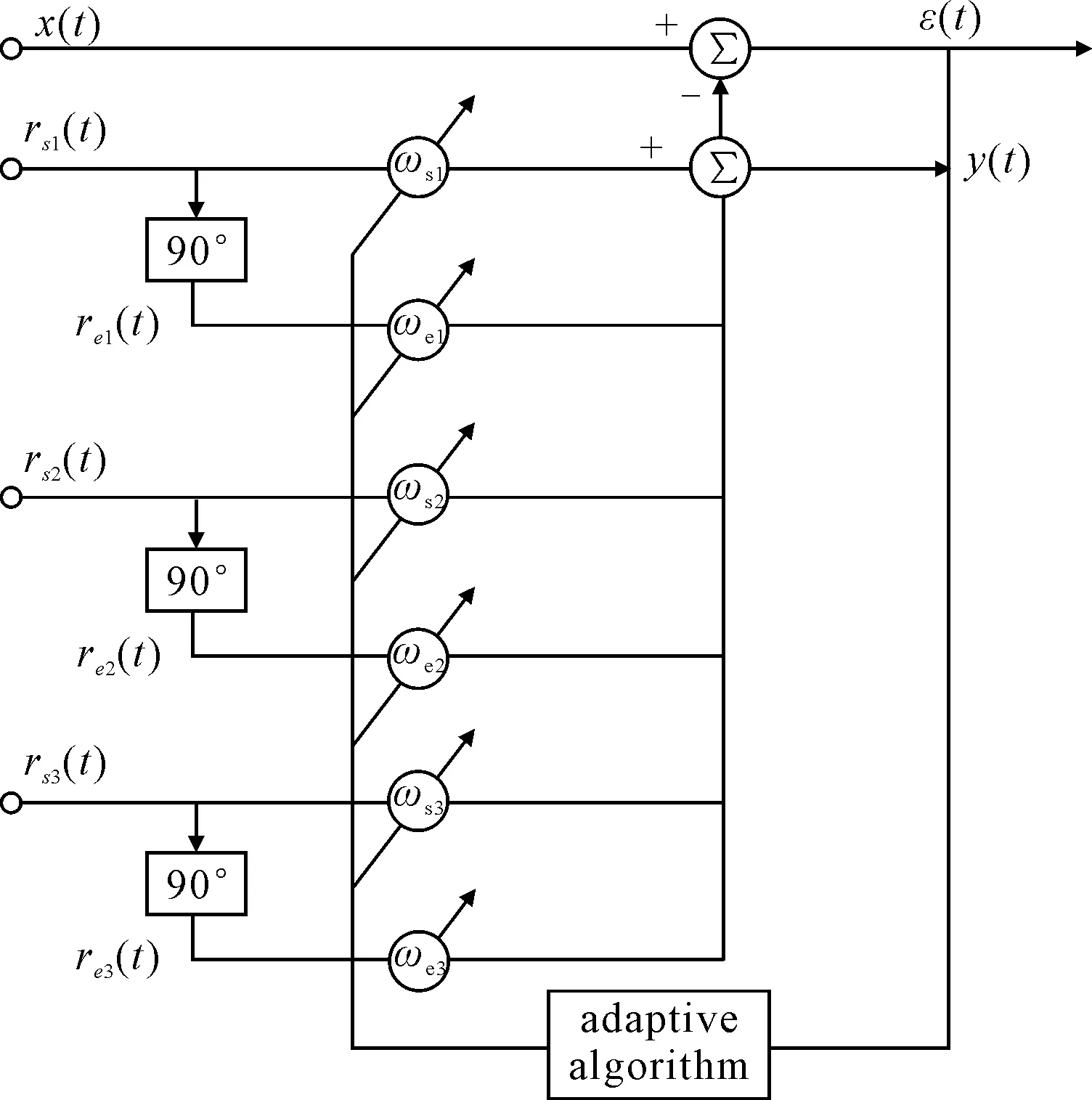
图2 3路并联的Notch滤波器

对每一个应答器，X(t)为基阵接收的信号。

X(t)=Bcos(ω0t-φ)+n(t)

(5)

式中：n(t)为背景噪声。

ri(t)为两路正交的参考信号，y(t)为参考信号正交信号的内积，ε(t)为接收信号与参考信号内积的误差。对参考信号的频率已知，分别对应单个应答器发射信号的中心频率。

rs(i)(t)=Asinωit

rc(i)(t)=Acosωit

(6)

式中：A为参考信号的幅值，下标i代表应答器的身份编号，i=1、2、3。

基阵接收的每一路信号都要通过3路并联的Notch滤波器，选择合适的自适应算法，通过滤波器的输出结果就可以检测出发送该信号所对应的应答器。然后通过相位差估计器解算出该信号在基阵相邻阵元间的相位差。

(7)

式中：下标i代表应答器的身份；m、n代表基阵中相邻的阵元。

2 仿真计算

通过仿真计算来验证USBL对应答器进行定位解算待沉管节平面位姿的有效性。仿真中，USBL定位系统测时误差取值为0.1 ms，定位精度误差取值为0.1%斜距。待沉管节上安装有3个不共线的应答器，组成一个直角三角形，管节平面相对于USBL基阵坐标的欧拉旋转角度设置为θx=5°,θy=10°,θz=15°。

通过上述位姿解算方法，求解出待沉管节平面相对于USBL基阵的欧拉角：θx=4.95°,θy=10.04°，其中绕Z轴的欧拉角出现无解状态，这是由于方向余弦矩阵有9个分量，实际只有3个自由度，假设欧拉角为未知量，通过法向量直接求解方向余弦矩阵，则使得矩阵为非满秩阵，从而出现绕Z轴欧拉角度无解的状态。为此，配合应答器初始位置，并通过已解算出来的θx、θy值，再解算绕Z轴的欧拉角，最终得到管节平面绕Z轴旋转的欧拉角。仿真求解的欧拉角均值：θx=5.001 4°,θy=10.038°,θz=15.78°，计算误差：Δθx=0.01°,Δθy=0.02°,Δθz=0.03°。见图3。

图3 管节平面位姿角度仿真计算结果(基阵坐标系)

2.1 姿态角估计精度

管节姿态角估计精度与超短基线定位精度有直接关系，因此仿真验算了定位精度和姿态角估计精度之间的关系。仿真步骤：沉管在大地坐标系下的欧拉角精确值为[5° 10° 15°]，改变超短基线定位系统的定位精度，求姿态角的误差。以绕X轴姿态角误差为例，结果见表1。

表1 USBL定位精度与绕X轴欧拉角的关系

表1中R为基阵坐标系原点到局部坐标系原点的斜距。由表1可见，超短基线定位精度由0.050R增加到0.001R时，回收平台姿态角度误差也就越来越小。在水文环境较好的背景下，基于Notch滤波器的超短基线定位系统的精度高于0.010R时，此时姿态角误差达到了0.010°，可以满足工程需要。

2.2 沉管表面应答器个数

理论上3个应答器即可决定沉管的定位面，且应答器个数越多，冗余信息量增加，参数估计的精度有相应提高。但应答器个数太多，会增加成本和计算复杂度。为了研究应答器个数和姿态角估计精度之间的关系，进行了如下仿真计算：改变应答器的个数，对每个应答器的位置进行解算。每增加一个应答器，就利用新的冗余信息对前一次计算的欧拉角进行修正，求解管节平面的姿态角(以绕X轴欧拉角为例)，见图4。

图4 管节平面安装应答器个数与姿态角度(绕X轴)误差的关系

图4表明，当应答器个数从3增至1 000个，姿态角估计精度也逐渐提高。但精度的提高仅在极小的量级，最高不超过0.020°，不符合工程实际。并且由仿真可知，当定位精度高于0.010R时，安装3个应答器的角度估计误差便小于0.010°。

2.3 应答器的布放

除应答器个数，还需考虑应答器布放位置和姿态角估计精度之间的关系。根据几何关系，不共线3点能决定一个平面，因此只需要3个应答器位置不在一条直线上，理论上都是可以解出唯一平面。为了研究应答器布放位置和姿态角估计精度之间的关系，进行了如下仿真计算。仿真步骤：改变应答器的布放位置，采用三种构成形状，计算欧拉角估计误差，见表2。

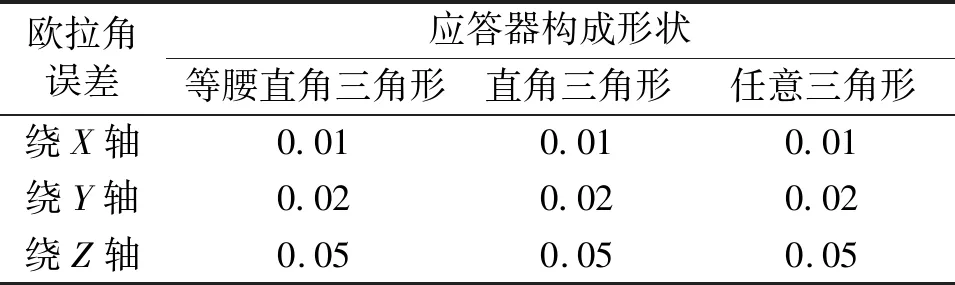
表2 应答器构成形状与姿态角估计的关系 (°)

由表2可见，应答器的布放形式对姿态估计精度没有影响。这一结论使得应答器在沉管上的安装变得更为方便，可以根据施工要求灵活选取，避开高噪声区。同时，可将应答器安装在USBL定位精度较高的基阵正下方，有助于提高位姿算法的精度。

3 结论

相比于单一的传统沉管下沉测控方法，本文提出基于USBL定位系统的管节沉放测控方案，在管节下沉阶段可辅助待沉管节较为精确地布放到待沉区域(粗测阶段)，而后结合高精度相对法完成最终的对接定位过程(精测阶段)。该方案的优势如下。

1)满足远岸、深水的沉管施工要求。超短基线声学定位系统不依靠岸基上的辅助设施，摆脱了离岸距离的限制。同时，与传统定位方法相比，在深水区依然满足施工精度。与GPS系统结合后，可以实时显示沉管在大地坐标中的三维姿态参数，可有效辅助远岸、深水环境下的沉管水下沉放施工。

2)设备成本低，安装方便，作业安全性高。超短基线声学定位系统体积小、成本低廉。作业前只需要在沉管上表面按需求安装3个应答器，无需安装测量塔，安装过程在水面进行，可减少施工人员下水作业次数。整个施工过程效率高、安全性高、操作复杂性低。