基于Kriging算法的虚拟应答器捕获方法
2022-06-10韩思成陈永刚熊文祥
韩思成,陈永刚,熊文祥
(兰州交通大学 自动化与电气工程学院,兰州 730070)
0 引言
虚拟应答器(virtual balise, VB)是国际铁路联盟为了减少列控系统成本,将全球卫星导航系统(global navigation satellite system,GNSS)应用到列车定位中的装置。目前中国列车控制系统(Chinese train control system, CTCS)等级2和等级 3中,为了防止报文数据的丢失或者应答器出现故障,应答器需要高密度布设在轨道上。虚拟应答器可以减少实际应答器在轨道上的铺设,降低了设备成本和日常维护费用。
虚拟应答器在工作的过程中,最重要的是对虚拟应答器进行捕获,国内外目前对虚拟应答器的捕获研究取得了一些进展,文献[2]研究了GNSS接收机输出频率、列车速度与虚拟应答器捕获率之间的关系,并提出了大捕获区域和小捕获区域的概念;文献[3]研究了考虑定位误差下的虚拟应答器捕获识别;文献[4]提出了几何统计测试的虚拟应答器捕获判别方法;文献[5]提出了一种新的VB捕获方法,实现了无需选择唯一的捕获间隔,降低捕获误差和时间偏移;文献[6]采用圆概率误差计算方法和列车运动数学模型,确定虚拟应答器点的位置和捕获半径的选择;文献[7]提出了虚拟应答器基于速度和加速度的预测捕获算法,并对捕获算法进行了测试验证。然而,现有的虚拟应答器捕获方案中,虚拟应答器在出现漏捕获后,列车继续前进,并未对遗漏的虚拟应答器进行任何处理。克里金(Kriging)算法不仅拟合效果良好,而且具有较好的连续性和可导性,仅用少量样本点即可获得良好的插值拟合效果,故具有广泛的应用前景。文献[9]通过改进的Kriging插值算法提高了煤矿井下定位的精度;文献[10]利用 Kriging插值算法将地磁基准图性能进行了优化;文献[11]提出了一种基于Kriging插值的孔位修正方法,使孔位估计误差满足航空装配要求。
基于此,本文提出了一种基于Kriging算法的数据内插方法,在 GNSS接收机提供有限样本个数的环境下,能够有效地利用样本中的数据信息,对已知的样本点集合进行插值扩展。通过设置仿真场景将该方法与不同 GNSS接收机频率下的虚拟应答器捕获方法进行了比较,验证了本文所述算法在虚拟应答器捕获率和捕获精度等方面具有显著的优势。
1 虚拟应答器概述
1.1 虚拟应答器结构组成
虚拟应答器工作原理如图1所示。
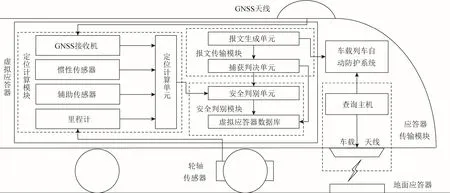
图1 虚拟应答器工作原理
图1的定位计算模块主要接收 GNSS信号,实时计算定位数据,对数据进行信息融合处理;安全判别模块主要检测当前定位坐标与下一虚拟应答器(next virtual balise, NVB)坐标进行比较,如果当前的定位误差在一个安全合理的范围内,则将定位信息传递给报文传输模块;报文传输模块则根据定位信息在虚拟应答器点处对虚拟应答器进行捕获,捕获判决单元如果判定虚拟应答器被捕获,报文生成单元立即向车载列车自动防护系统(automatic train protection,ATP)发送和实际应答器相同的报文。
1.2 虚拟应答器捕获半径
虚拟应答器功能结构中最核心的部分就是对虚拟应答器进行捕获,但由于定位点是离散的,列车在正常运行情况下很难在 VB点处刚好接收到定位信息,因此,需要以VB点为中心设定捕获区域,如图2所示。
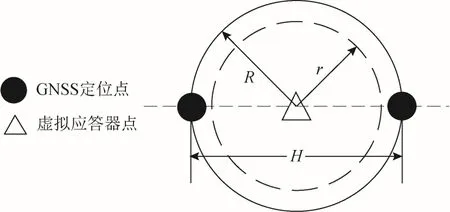
图2 虚拟应答器捕获半径示意图
当定位点落在捕获区域内,虚拟应答器即被捕获。若捕获半径为,易出现虚拟应答器漏捕获,为了能在 2个定位点间将虚拟应答器捕获到,则虚拟应答器的捕获半径至少是 2个定位点间的距离的一半,捕获半径的计算公式为
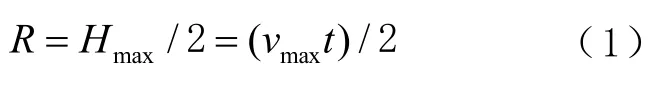
式中:为 2个 GNSS定位点距离的最大值;为列车最高运行速度;为GNSS接收机采样间隔。
图3为虚拟应答器漏捕获状态。
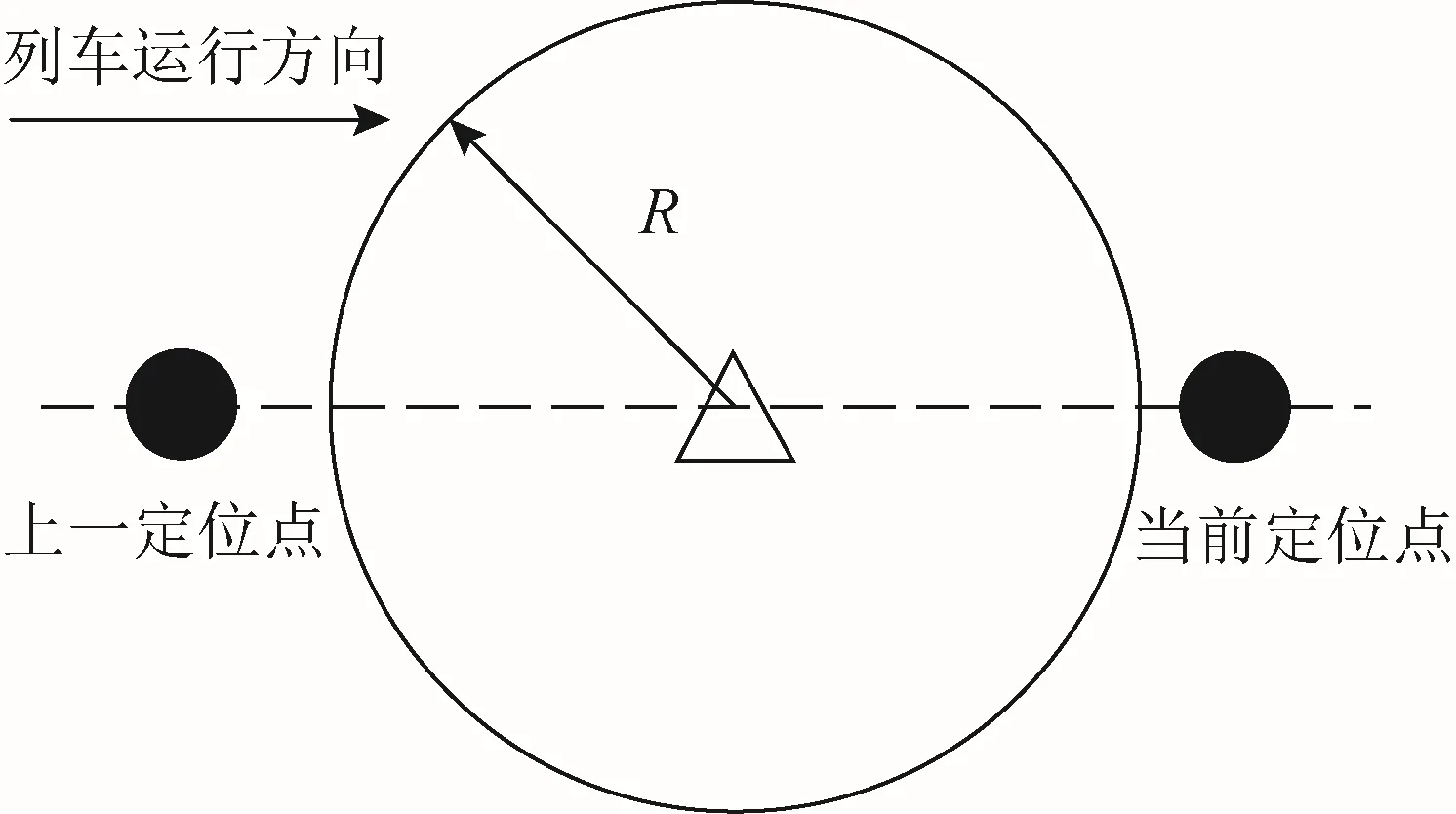
图3 虚拟应答器漏捕获状态
当虚拟应答器处于漏捕获状态,车载 ATP将接收不到提供行车许可、线路参数、等级转换等信息包,无法生成动态速度曲线,监控列车运行安全,严重影响行车安全。图4为虚拟应答器重捕获状态。
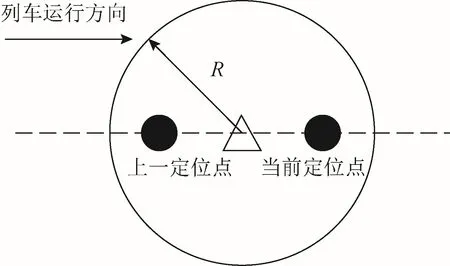
图4 虚拟应答器重捕获状态
当虚拟应答器处于重捕获状态,车载ATP将接收到重复相同的报文,增加了系统处理的压力。
当前虚拟应答器漏捕、重捕的风险仍然存在,在现有研究中,主要是针对虚拟应答器的捕获状态进行预测,当虚拟应答器被遗漏后,列车继续前进,尚未对已经漏捕的虚拟应答器做出任何的操作。
2 基于Kriging算法的数据内插方法
本文采用了基于Kriging算法的数据内插方法,使虚拟应答器点能够在捕获区域内被捕获,进一步提高虚拟应答器的捕获率和捕获精度,保障列车安全可靠运行。
首先判定虚拟应答器是否处于漏捕获状态,如图5所示。

图5 漏捕获判定示意
虚拟应答器漏捕获状态的判断条件为:>,>且>。
图5中为2个GNSS定位点之间的距离;为虚拟应答器点与上一定位点的距离;为虚拟应答器点与当前定位点的距离。
当虚拟应答器处于预捕获状态也满足>,>,但<,如图6所示。

图6 预捕获判定示意
假设在列车运行的线路上一共设置了个虚拟应答器,虚拟应答器点的坐标为(,b),(=1,… ,), GNSS接收机一共采集到个定位点,坐标为(,) , (= 1,… ,),如图7所示。
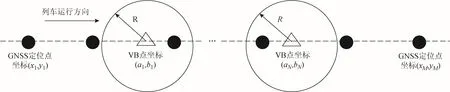
图7 算法案例示意
Z为第个 GNSS定位坐标点和第个虚拟应答器坐标点之间的距离,Z的计算公式为
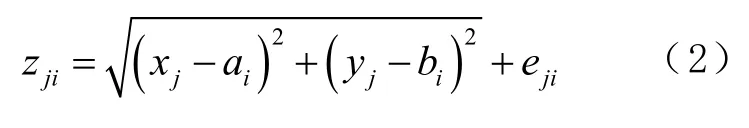
式中,e为系统误差。

式中,λ为权值系数。
Kriging算法的关键是求出权值系数λ的值。Kriging方法的目的是要使ˆ为待估计点(,)处,真值的无偏估计,则估计量的数学期望等于被估计参数的真实值,其计算方法为

将式(4)带入式(3),可以得

在无偏性下,通过拉格朗日乘数法让估计方差最小,首先构造目标函数为
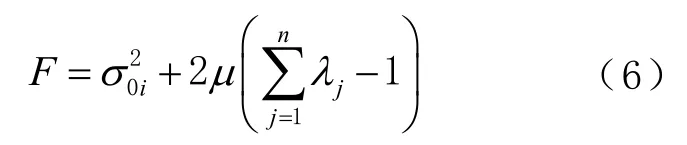
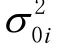
将式(6)中的和λ同时求偏导,如式(7)所示,可以得到Kriging方程组如式(8)所示。
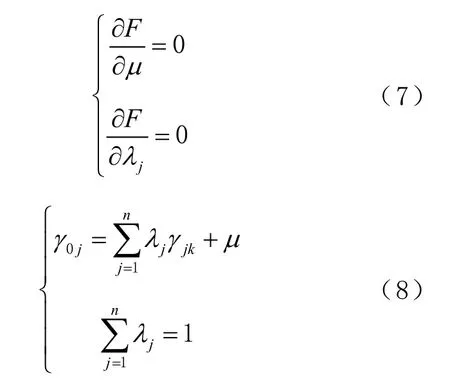
式中:为−x的变差函数;γ为−x的变差函数。
将式(8)其写成矩阵形式,如式(9)所示,简记为=
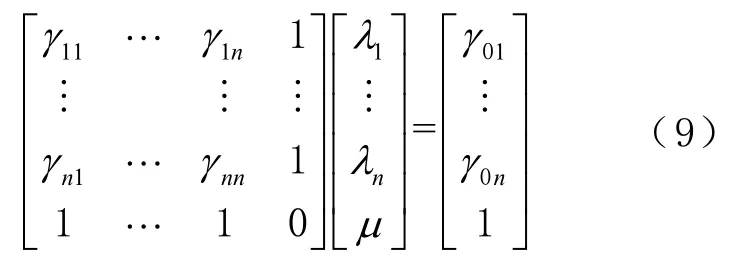
将式(9)进行求解,可得权值系数,的矩阵计算公式为
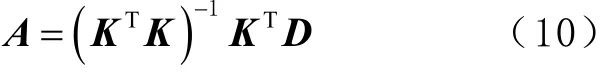
变异函数用来描述两点间距离为的相关性,通过求解变异函数()来求解式(9),变异函数的计算公式为
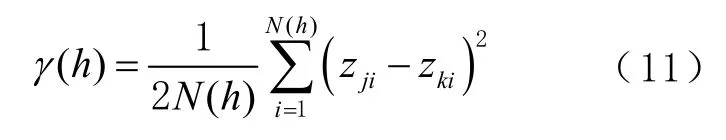
式中:()为 GNSS定位点之间的距离小于的数目;Z为第个GNSS定位坐标点和第个虚拟应答器坐标点之间的距离。
因为式(11)不能反映出在不同区域下滞后距离上的变异特征,需采用拟合模型对已知样本点离散关系进行拟合,本文采用变异函数的指数模型将其进行拟合,变异函数指数模型公式表达式为

式中:为变异函数曲线在()轴的截距;为变异函数达到稳定时的增量;为变异函数第1次到达稳定时所对应的采样距离。
假设虚拟应答器目前已处于漏捕获状态,如图8所示。

图8 数据内插示意
首先根据 2个 GNSS定位点的坐标,通过Kriging算法算出权值系数,生成拟合曲线,得到ˆ的表达式,取插值点的横坐标=a,得出插值点的纵坐标进行内插。
由于算法在判断虚拟应答器出现漏捕获后再进行数据内插,不可避免造成捕获延迟,同时GNSS接收机和虚拟应答器系统本身也有延迟,解决方案如图9所示。

图9 捕获延迟解决示意图
将虚拟应答器的设置点前移一段距离,的计算公式为

式中:为列车最大运行速度;为捕获延迟时间,目前大部分虚拟应答器延时<0.5 s。
虚拟应答器的捕获时间的计算公式为
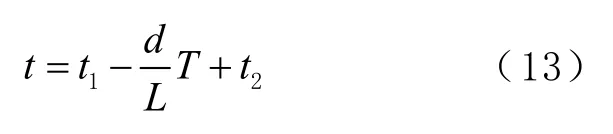
式中:为采样周期;为当前定位点的时刻;为当前定位点与插值点间的距离。
3 仿真验证
本次仿真的研究对象为 CRH380B型动车组,其具体参数如表1所示。

表1 CRH380B型动车组参数表
本文仿真所采用的列车速度曲线如图10所示。列车一直处于变速的运行状态,设定每2个虚拟应答器之间的距离为3 000 m,共设置33个虚拟应答器,列车最高时速300 km/h,行驶里程100 km,由于捕获延迟,仿真中虚拟应答器全部设置在原设置点与列车运行相反的方向前移43.06 m的位置。
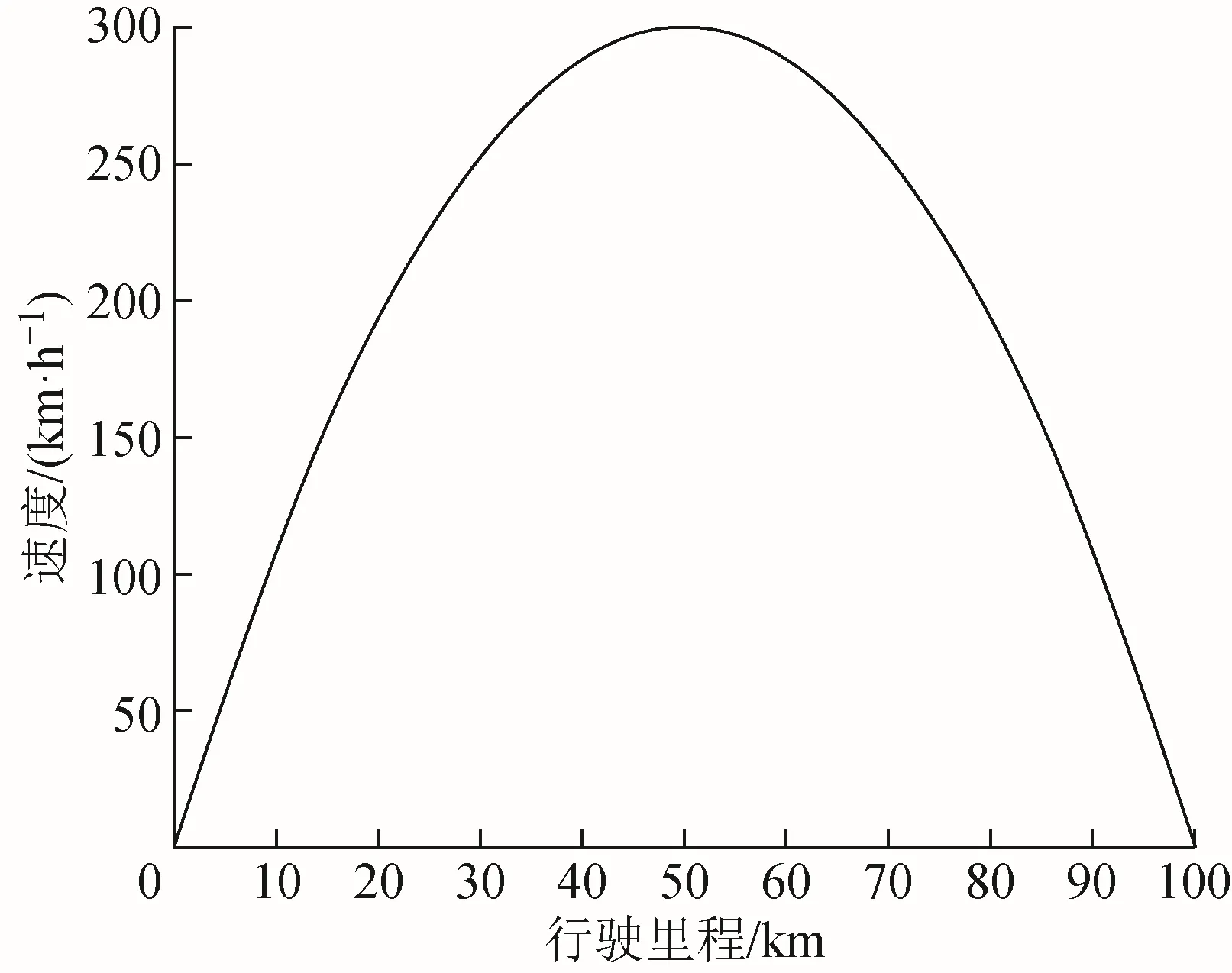
图10 仿真速度曲线
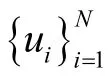
1)u=0,虚拟应答器尚未被捕获;
2)u=1,虚拟应答器已被捕获。
虚拟应答器捕获率指已捕获的虚拟应答器与总虚拟应答器数目之比,捕获精度指轨道地图上虚拟应答器点与捕获定位点之间的距离。
当捕获半径为5、10 和20 m时,为了验证本文提出的基于Kriging算法进行数据内插的捕获性能,选取了不同 GNSS接收机频率对虚拟应答器捕获状态、捕获率和捕获精度进行对比,GNSS接收机频率选取了4个典型值(1、2、5、10 Hz)的结果如图11至图15所示。
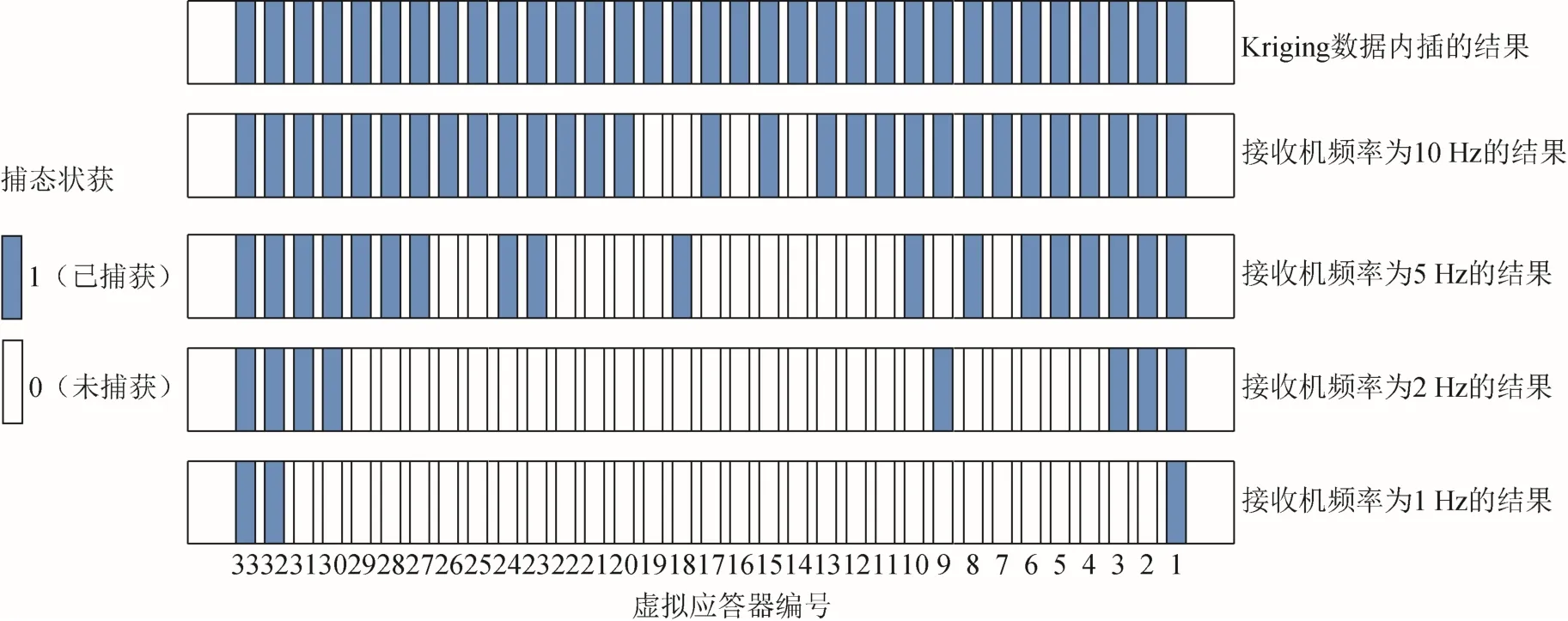
图11 捕获半径为5 m时不同捕获方案下捕获状态比较
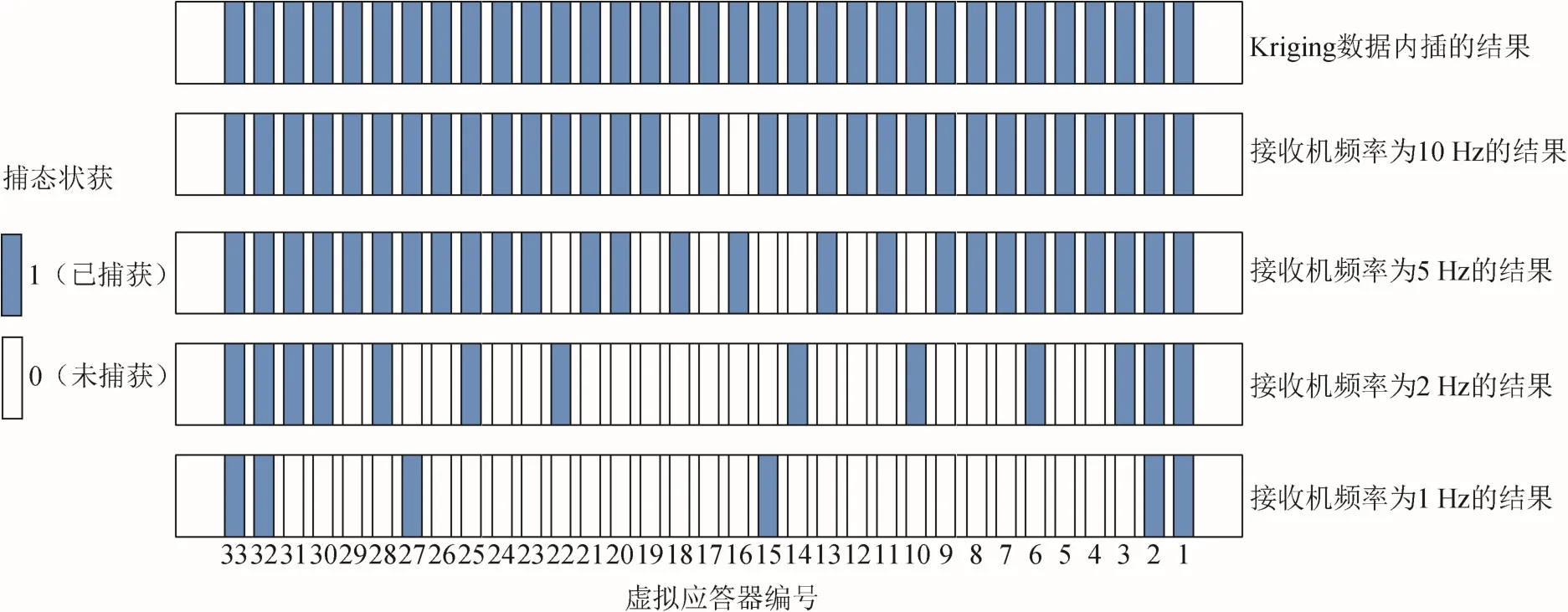
图12 捕获半径为10 m时不同捕获方案下捕获状态比较
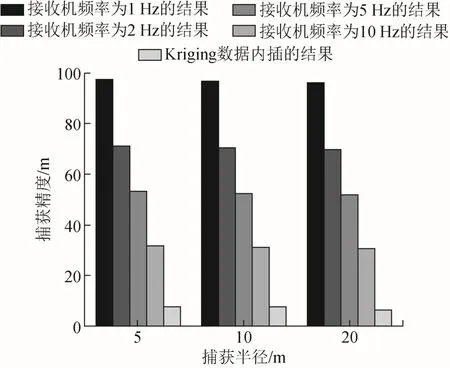
图15 捕获半径为常量时不同捕获方案下捕获精度比较
从图11至图13中可以看出,在100 km内,虚拟应答器发生漏捕主要出现在列车速度较快的区段,且GNSS接收机频率越低,虚拟应答器漏捕获越严重,即使GNSS接收机的频率达到最高10 Hz时,仍有少许虚拟应答器出现漏捕,车载ATP接收不到报文,影响行车安全。通过Kriging算法进行数据内插,可以很明显地解决虚拟应答器出现漏捕的情况,保障列车安全平稳行驶。
图13 捕获半径为20 m时不同捕获方案下捕获状态比较
从图14中可以看出,在100 km内,Kriging插值算法的捕获率稳定保持在 100%,反映了该方法在虚拟应答器出现漏捕获状态后插值点能够在捕获区域被捕获。其他不同GNSS接收机频率下的捕获方案虚拟应答器都会出现一定程度的漏捕。

图14 捕获半径为常量时不同捕获方案下捕获率比较
从图15中可以看出,在 100 km内,虽然Kriging插值算法与GNSS接收机频率为10 Hz的捕获精度都达到了 ETCS规定的 2.6 m之内,但Kriging插值算法的捕获精度更高,误差更低。
4 结束语
针对目前 GNSS接收机提供的定位数据是离散的,虚拟应答器易出现漏捕获现象,本文提出了一种基于Kriging 算法的数据内插方法,对有限的样本数据进行插值扩展,使遗漏的虚拟应答器仍能在捕获区域内被捕获,仿真结果表明,在相同捕获半径条件下,Kriging 插值算法的捕获率稳定保持在100%,反映了该插值算法应用于虚拟应答器漏捕获的可行性。同时Kriging 算法进行数据内插与不同 GNSS接收机频率捕获虚拟应答器相比,捕获精度更高。
