基于单元等长的船体曲板展开方法

(1.上海交通大学 a.海洋工程国家重点实验室；b.高新船舶与深海开发装备协同创新中心，上海 200240；2.大连船舶重工集团有限公司，辽宁 大连 116021)

船体曲板展开为钢板的号料套料提供依据，影响着曲板加工成形的工艺操作，是船舶建造过程中的重要环节。有效的曲板展开方法[1-7]，可以获取精细的钢板号料方案，推进船厂无余量造船进程。目前国内一些船厂采用的展开方法仍是手工放样或计算机模拟手工放样，利用由此得到的板材展开图进行后续船体曲板成形加工时，需要加入一定余量，影响后续工艺环节的加工效率。为此，提出一种基于单元等长的船体外板展开方法，在低应变能情况下，减少外板展开的面积误差，以期为后续三维曲板加工成形提供有效的支持。

1 展开方法

船体曲板大多为不可展开的复杂曲面，需要将其分割为多个微小区域逼近原曲面，将各个微小单元进行展开，获得最终的近似展开平面。曲面展开根据展开目的的不同，所采取的展开方法也不尽相同，常见的展开方法有保证面积恒定，保证长度恒定和保证角度恒定等。船厂工程实际中主要采用手工测地线法、垂直准线法和撑线法等展开三维曲面，其本质的展开方法均基于保证展开单元的长度恒定。但是由于船厂实际操作中为手工作图，往往需要留有一定余量，是不完全的保长展开方法。

在船厂实际使用的不完全保长展开方法的基础上，对三维曲板进行了网格划分，采用四边形单元长度恒定展开方法对船体三维曲板进行展开。在展开过程中，需要确定展开基准线，将三维复杂曲面围绕基准逐步展开，展开策略的不同导致对展开基准线的选择也不尽相同。如图1，在三维曲面中以两条相交曲线为展开基准线，基准线为三维曲面上的空间曲线，保证基准线中的单元节点间在展开图中的距离与实际距离相等，并从两条基准线出发按照展开前后构成单元长度恒定的方法，依次展开，获取最终的展开曲面。

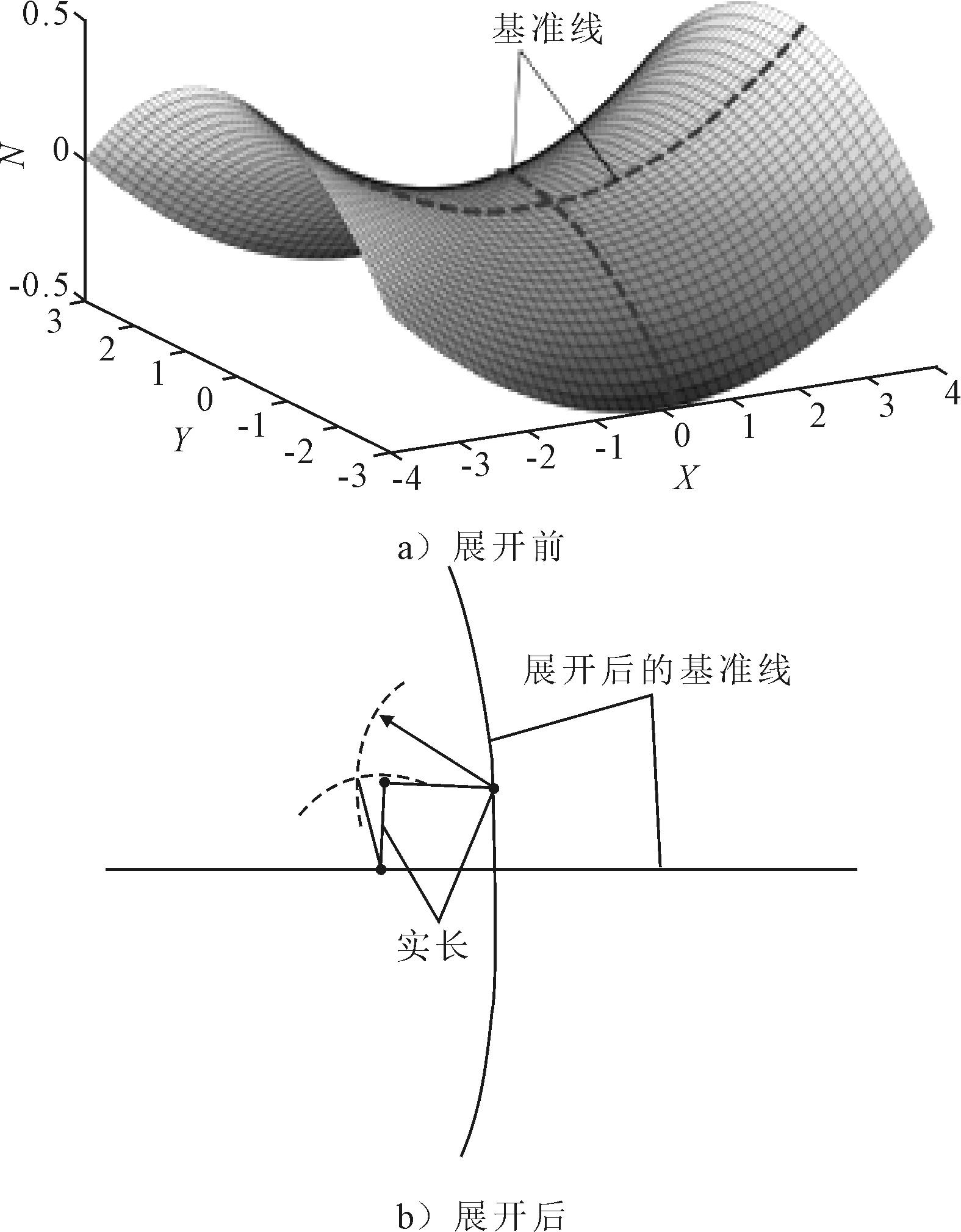
图1 单元等长度的展开方法示意

2 展开步骤

1)从肋骨型线图中获取待展开船体曲板的型值数据，对数据进行单位调整和初步处理。

2)利用NURBS拟合曲面并划分网格。

3)计算基准线。纵向基准线为中间肋骨型线，按照经典的测地线法对其进行展开同时保证各个单元节点间长度为实长。横向基准线为贯穿曲面的一条空间曲面，是曲面内两点间的最短面内距离，因此在展开平面中横向基准线为一条直线。

4)展开基准线和其他单元。以2条基准线的交点为中心点，对基准线进行展开，横向基准线展开后为一条直线，纵向基准线展开方法则在经典测地线法展开方法的基础上进行改进，通过计算各个单元节点的肋骨弯度对纵向基准线进行了展开。最后通过两条已经展开的基准线，按照单元等长原则对其他单元节点进行展开。

2.1 网格划分

通过NURBS曲面对待展开三维曲面进行插值拟合，通过节点矢量、控制网格点和权值控制拟合曲面，NURBS曲面方程如下。

(1)

式中：(u,v)∈[Umin,Umax]×[Vmin,Vmax]；Pi,j为控制点；Wi,j为权重；Ni,p(u)为u方向p次B样条函数；Nj,q(v)为v方向q次B样条函数；Cu和Cv为控制点数。

利用NURBS曲面算法对输入的肋骨型值进行插值拟合，获取更多的曲面节点，绘制出三维曲面图，方便后续的展开、应变和面积的计算工作。完成对曲面的网格的初步划分，获取各个控制节点的坐标，在求取基准线算法中还需要进行网格的局部细分，都是通过NURBS曲面进行的。

2.2 基准线的计算

参考测地线法展开船体曲板选取展开基准线的方法[9]，在待展开的三维曲面中选取中间肋骨型线为纵向基准线。选择曲面内的两点间的测地线为横向基准线，起始点选取测地线法中所作测地线的两个端点，然后通过改进的迪杰斯特算法求解出该两点间的最短曲面距离路径，将其作为待展开曲面的纵向基准线，从而完成基准线的确定工作。

迪杰斯特算法是经典的最短路径算法，主要策略为按照路径长度依次增长计算出起始点到各个其他节点的最短路径，具体步骤如下。

步骤1。初始化集合S和U，集合S中只包含起点Pstart，U为S在全集中的补集。

步骤2。遍历U集合计算U(i)到起点Pstart的距离，选取距离最短的定点Pshort加入集合S，并重新计算集合U。

步骤3。更新集合U中各点到起点Pstart的距离，重复步骤2至便利完所有定点。

步骤4。输出横向准线长度D和路径R。

Dijkstra算法要求待展开曲面的网格划分较为精细，耗费大量的计算资源。因此，选择局部细分网格的策略节省计算资源的同时获得高精度的结果。在初始网格密度条件下，使用迪杰斯特算法进行初步求解，求解的最短曲面距离为Di。对迪杰斯特算法求解出的横向准线所经过的单元区域进行标记，然后仅对标记的区域进行网格细分，再利用迪杰斯特算法在标记区域内进行进一步求解，求解得到最短曲面距离为Di+1。循环进行局部网格细分求解，直到Di+1-Di<ε(ε为允许误差值)时退出循环，得到最终的横向基准线。

2.3 展开过程

横向基准线在展开图中应为1条直线，以2条基准线的交点为展开中心，保证横向基准线上单元节点间的距离恒定，展开横向基准线同时获得各节点在展开图中的坐标值。

纵向基准线是肋骨中间线，其展开方式是在经典测地线法的基础上进行改进。展开原理示意见图2a)。由于船体曲面多为复杂的不可展曲面，在展开过程中假设的圆柱外板母线与船体中心线不平行，展开后的肋骨线与准线不垂直，在展开图中肋骨曲线与过其弦线的法面展开线间存在一定的间距[8]，其中最大的拱度即为肋骨弯度S。纵向基准线的展开是基于肋骨弯度Si，保证该单元节点到O0的实长相等将其展开。

对其他单元进行展开，见图2b)，通过确定单元节点的位置从而确定整个单元展开形状的策略进行展开。

图2 展开过程示意

3 展开实例

以确定四边形单元Ai,jAi-1,jAi-1,j+1Ai,j+1为例，介绍一般四边形单元展开过程。根据单元等长的展开准则，在展开平面内找到一点Ai,j使得Ai,jAi-1,j和Ai,jAi,j+1展开前后长度恒定，由此即可确定点Ai,j的位置。

以船体建造过程中的帆型板为例，板材的型值见图3a)，NURBS曲面对进行曲面重构和网格划分，网格单元为四边形，共划分6 100(100×61)个网格，见图3b)。

通过经典测地线算法求解出横向基准线的端点坐标如下。

A(1.20×105,2 345.85,1.88×104)；

B(1.34×105,2 454.79,1.87×104)。

以此为输入参数，进行基于单元等长的展开算法运算。

如图4，设置改进迪杰斯特算法可接受误差为0.1 mm，即相邻两次计算结果差的绝对值不超过0.1 mm方可退出循环。

图4 改进迪杰斯特算法结果收敛

输出最终结果，最终经过9次迭代算法结果收敛，得到A与B间的最短曲面距离为13 639.34 mm，确定展开基准线后将其他单元节点也进行展开，获得最终的展开平面，见图5。

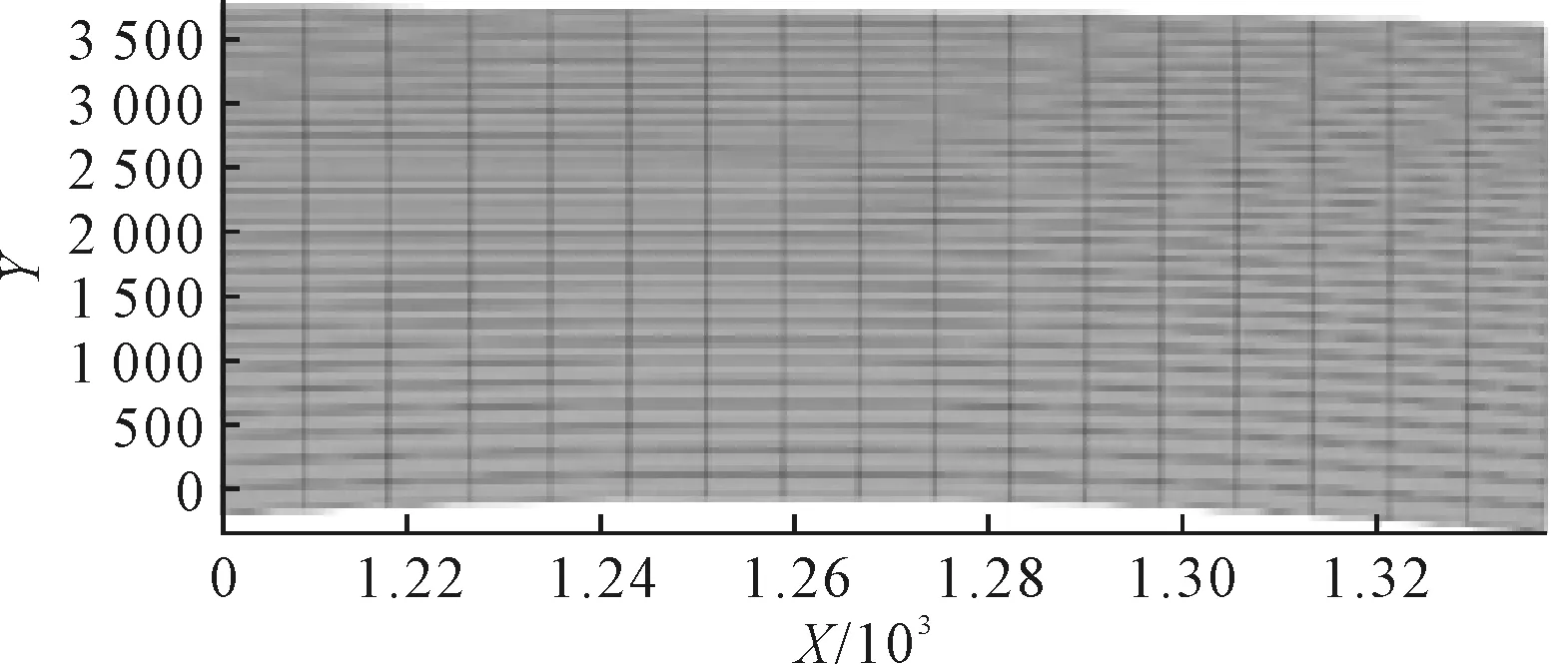
图5 最终展开平面

曲面展开后需要经过水火弯板等加工工艺方法将平面板材加工为具有一定曲率的三维曲面，在加工过程中板材厚度方向几乎没有变化[9]，因此板材加工前后表面积不变。曲板展开过程是曲板成形的逆过程，同样要求展开曲面与三维曲面的面积相近，因此往往通过面积误差来评价展开方法的可靠性和适用性。此外，应变能可以反应出曲板成形过程中的加工工作量，应变能越低说明曲板展开方案实用性越强。按本文方法展开结果与经典测地线法的数据对比见表1，单元等长展开法的面积误差控制为0.07%，相比于经典的测地线法有所提升。同时单元等长展开法中单元的平均应变能系数为7.316 9×10-4[10]，相比经典测地线法有大幅度改进，可以看出基于单元等长的船体曲板展开方法具备可靠性和适应性，符合工程实际要求。

表1 展开结果评价指标

4 结论

提出通过网格划分、基准线确定、基准线展开和单元展开等步骤实现对船体三维曲板的展开。本方法充分考虑船体三维曲板的套料和加工成形的后续工艺环节，计算四节点等参单元的应变能系数和展开面积误差两个评价指标，通过与测地线法进行对比，验证了单元等长展开方法可靠。