共轭解析函数的一个求法的注记*

黄 炜

(宝鸡职业技术学院, 陕西 宝鸡 721013)

0 引 言

古老的复变函数起源于19世纪，从柯西起至今有150多年的历史，已发展出许多新分支、新领域和新方法，如今复变函数成为数学中不可或缺的重要组成部分．解析函数是复变函数论起初所研究的主要对象(见文[1])．文献[2]提出来共轭解析函数概念，与解析函数对称．解析函数所能解决的所有问题共轭解析函数都可以用来解决，共轭解析函数比解析函数更直观方便．不少文献[3-4]已对共轭解析函数进行了研究，本文在前面研究的基础上．给出了共轭解析函数充要条件及求共轭解析函数一个新方法．

1 相关定义

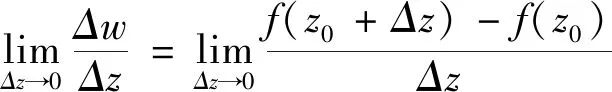
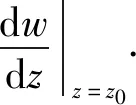
若f(z)在z0的δ邻域(z0,δ)内可导,称z0为解析点，否则称为奇点 ．

若f(z)在D内处处解析，则称f(z)在区域D内解析.

这时称函数w=f(z),z∈D于z点共轭可导或共轭可微[2]．

2 结 论

定理2设函数f(z)=u(x,y)+iv(x,y)在区域D内共轭解析，则：

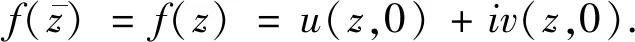
3 定理的证明

为了完成定理的证明需要下面的引理：

引理3.1函数f(z)=u(x,y)+iv(x,y)，则其形式导数为

证明：

设f=u+iv,则Δf=f(z)-f(z0),Δf=Δu+iΔv.

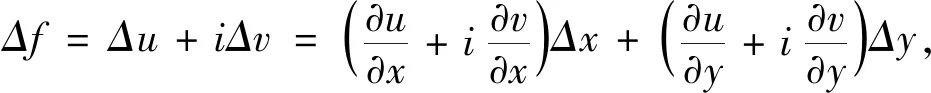
3.1 定理1的证明

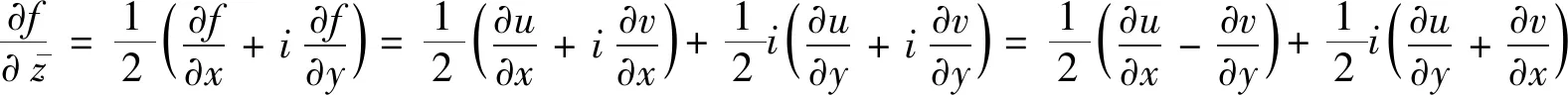
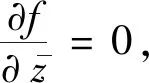
3.2 定理2的证明

因为f(z)在区域D内解析，故

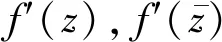
=u(z,0)+iv(z,0).

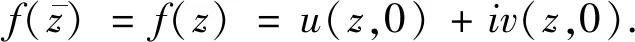
4 应 用

例4.1已知解析函数f(z)实部为u(x,y)=x3-3xy2,求f(z).

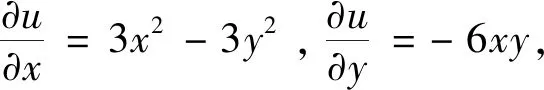
由线积分法可得：

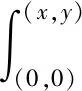
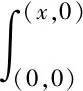
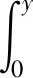
=3x2y-y3+C.

故：f(z)=u+iv=x3-3xy2+i(3x2y-y3+C).

令x=z,y=0,得

f(z)=(x+iy)3+iC=z3+iC.

例4.2已知解析函数f(z)的实部为u(x,y)=x3+6x2y-3xy2-2y3,且f(0)=0, 求f(z).

又因为函数f(z)解析，满足Cauchy-Riemann方程，由全微分法，得：

=-(6x2-6xy-6y2)dx+(3x2+12xy-3y2)dy,

则

=(3x2y+6xy2-2x3)+(3x2y+6xy2-y3)

-(3x2y+6xy2)+c

=3x2y+6xy2-2x3-y3+c.

故f(z)=(x3+6x2y-3xy2-2y3)+i(3x2y

+6xy2-2x3-y3+c)

=(x3-3xy2)+i(3x2-y3)

+2[(3x2-y3)+i(3xy2-x3)]+ic.

令x=z,y=0,得f(z)=z3-2iz3+ic,

因为f(0)=0,则c=0.于是

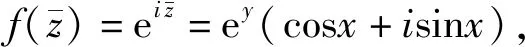
f(x)=cosx+isinx=eix=eiz.