基于直接关系图类方法的丙烯详细机理骨架简化

陈菲儿，邱 越，阮 灿，王文钰，吕兴才

(上海交通大学机械与动力工程学院，上海 200240)

计算流体力学(computational fluid dynamics，CFD)模拟由于开发成本低、设计周期短，且能提供实验研究不能提供的信息，是现代发动机的有效研究方法.但受限于计算机的运算能力，过于详细的动力学机理用于数值计算会导致网格无法精细化[1].反之，过于简化的模型对反应路径和中间产物的预测会产生较大的偏差[2].因此，为了更好地理解燃料在缸内的流动、喷雾以及燃烧，又兼顾运算成本，准确可靠地进行发动机的CFD 模拟，对燃料的详细化学动力学机理进行合理的简化具有重要意义.

近年来针对机理简化的理论和方法发展得非常迅速[1]，研究者已经针对汽油[3-5]、柴油[6-7]、生物柴油[8]等模型燃料机理进行了大量的简化工作.其中，骨架简化方法由于其简单高效的特点而被广泛应用，常见的骨架简化方法包括直接关系图(directed relation graph，DRG)法[9]、基于误差传播的直接关系图(directed relation graph with error propagation，DRGEP)方法[10]、路径通量分析(path flux analysis，PFA)方法[11]等.此外，Lu 等提出了两步DRG 法[12]与加上敏感性分析的直接关系图(directed relation graph-aided sensitivity analysis，DRGASA)方法[13]，Niemeyer 等[14]比较了DRGEP 方法中不同的路径搜索算法的影响，发现使用Dijkstra 搜索算法可以得到更优的简化机理.

发动机的性能和排放水平与燃料燃烧息息相关，理解碳氢燃料在低温和高压下的化学反应动力学对均质压燃(HCCI)和低温燃烧(LTC)等先进燃烧模式的研究具有指导意义.丙烯作为正庚烷和异辛烷等大分子碳氢燃料燃烧的重要中间产物[15-17]，其分解和氧化机理直接影响大分子碳氢燃料的反应活性和反应路径，对火焰传播也有一定的控制作用.此外，丙烯对多环芳香烃的形成和长大有着非常重要的影响[18-19].因此，理解全工况下丙烯的燃烧特性有助于深入理解大分子碳氢燃料的反应特性以及碳烟的生成和氧化过程，能在一定程度上揭示发动机不同燃烧阶段的火焰结构、中间产物和自由基的发展历程.

基于以上背景，本文耦合MATLAB 2017 b 与CHEMKIN-PRO 15131[20]，使用DRG、DRGEP、两步DRG 以及DRG 联合DRGEP 4 种方法，建立了一个详细动力学机理简化程序.对丙烯详细机理进行简化，构建了一个精度可靠、规模合理的丙烯骨架机理.选取最优的简化结果进行模拟，通过多个模型验证了该机理的可靠性与简化程序的有效性.

1 机理简化方法

1.1 直接关系图法

直接关系图法[9]借鉴了图论的思想，能从耦合的微分方程组中直接有效地量化组分间的相互影响.它将组分看作节点，组分之间的关系通过带权的有向边表示，从而形成一个有向图.组分之间的关系可以定量表示为

式中：RAB为组分B 对组分A 生成和消耗的影响；Nr为机理包含的反应总数；νA,i为组分A 在第i 个反应的计量系数；为第i 个反应的净反应速率.给定一个阈值ε，若 RABε＞，则认为去除组分B 会对组分A的生成和消耗带来较大影响，因此若组分A 保留，则组分B 也应被保留.通过设定初始的重要组分和阈值，可以从详细机理里筛选出与初始组分相关的重要组分集和相应的基元反应，剔除不重要的反应，最终得到一个骨架机理.

DRG 的实现方法是：对于每个样本点，由零维定容模型中得到的净反应速率和机理系数矩阵，依据公式(1)算出组分间相关性矩阵；再根据设定的筛选阈值ε将矩阵中小于ε的数置0，构建出一个有向图；然后利用深度优先搜索算法(depth first search，DFS)从初始组分集(本文中为燃料、O2、N2、H2O、CO2)出发进行搜索，得到与初始组分耦合的重要组分集合.将不同样本点的计算结果取并集，得到最终的反应组分集合，筛选出集合中包含的组分参与的重要反应，由此构建简化机理.

1.2 基于误差传播的直接关系图法

DRG 方法高效简洁、易于实现，但它仅仅考虑了组分之间的直接关系，忽略了沿路径传播时组分间相关性的减弱，DRGEP 方法[10]则考虑了路径长短带来的影响.设初始组分A 经过一系列中间组分到达B，这些中间组分构成路径p.在路径p 下，B 对A 的作用rAB,p可以表示为沿程两两组分相关性之积：

考虑组分A 到B 的全部路径，组分B 对A 的总作用定义为所有路径中的最大值：

文献[10，21]中详细分析对比了不同 rAB计算式带来的影响.本文在使用DRGEP 方法计算组分间相关性 rAB时，将组分A 的生成和消耗分开考虑：

DRGEP 的具体实现方法与DRG 相似，主要的不同在于得到相关性矩阵后，使用了Dijkstra 搜索算法来计算初始组分和其余组分之间的远近相互作用关系，之后剔除相关性小于阈值的组分，得到需要保留的组分集，生成最终的简化机理.需要注意的是，由于考虑了路径长短，不同的初始组分得到的组分间相关性是不同的，在使用DRGEP 方法时，初始组分的选取会对简化结果产生较大的影响.本文对丙烯的简化选取初始组分为燃料(C3H6)、O2、N2、H2O 和CO2.

1.3 详细动力学机理简化程序

本文提出的机理简化程序主要尝试对详细机理进行骨架简化，简化流程如图1 所示，简化过程中需要给出详细机理，选定用于简化的样本工况(温度、压力、当量比)以及简化机理的精度.简化机理的精度根据燃料在零维定容模型中着火延迟的最大相对误差(绝对值)量化，其中，着火时刻定义为反应过程中温度变化最大处.

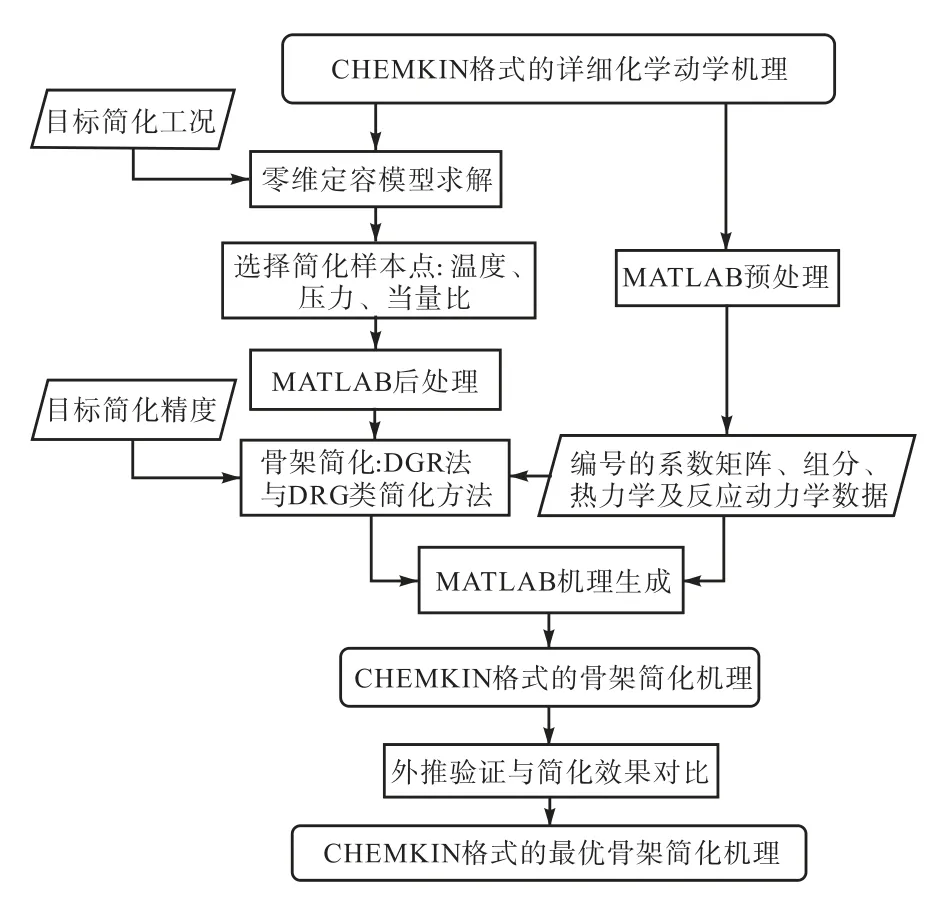
图1 机理简化流程Fig.1 Flowchart of mechanism reduction

首先，基于MATLAB 平台调用CHEMKIN-PRO求解器CHEM 进行详细机理阐释，将输入文件中包含的机理系数矩阵、组分、热力学数据、反应动力学数据等信息进行编号存储，以方便后续调用；随后，调用零维定容模型CK Reactor Generic Closed 求解，得到所选简化工况下的着火延迟时间以及净反应速率，这些是进行骨架简化需要的动力学数据；接着，调用不同的骨架机理简化方法，识别并剔除不重要的组分，并筛选出重要组分参与的重要反应，从而构建相应的简化机理.

删除一些组分之后，机理随之改变，式(1)、(4)中的 RAB值相应改变，而考虑多步的简化法能进一步简化机理[22].Lu 等[12]和Poon 等[23]的研究表明，两步DRG 法可以达到较好的效果.因此，除了DRG、DRGEP 算法，本文还使用了两步DRG 以及DRG 联合DRGEP 方法对详细机理进行简化.

设定不同的阈值可以得到一系列不同规模的简化机理，再进行准确性的验证，最终得到一个全局最优的骨架机理.在两步法中，第一步设定的阈值较小，一般在误差快速增大处，随后在第一步DRG 简化的基础上再应用DRG/DRGEP 方法进行简化.最后，对构建的简化机理进行验证，包括各个工况范围下燃料的着火延迟、LFR 平推流反应器中的重要组分浓度变化以及一维层流火焰速度等，进一步评估简化机理的准确性.

2 丙烯动力学机理的简化

2.1 简化工况与样本点选取

本文中丙烯的详细化学反应动力学模型采用AramcoMech2.0 机理，共包含493 种组分和2 716 个基元反应.该机理针对激波管、快速压缩机、射流搅拌反应器和流动反应器内的大量实验数据进行了验证.相对上个版本，这个版本的机理包含了更多大分子反应，对着火延迟和层流火焰速度等的验证有明显改善[24].值得一提的是，该机理针对丙烯扩展了实验的工况，可适用于更高压和更低温工况下的预测[25].

机理的简化通常是针对特定的工况进行的，因此简化工况的选取相当重要.本文旨在通过计算获得一个适用于较宽工况(尤其是较高压力)的简化机理，结合发动机三维CFD 模拟的常用工况，本文的简化样本点如表1 所示，共选取不同温度、压力和当量比下的90 个工况进行简化.

其中，温度点的选取按每个压力和当量比下着火延迟曲线的变化，沿程选取约10 个点，覆盖从低温到高温区间，由于丙烯几乎没有NTC 区间，因此每隔100 K 均匀选取温度点.压力1 MPa、当量比1 下的温度点选取如图2(a)所示.而对于同样的压力、当量比、温度，零维定容模型反应的净反应速率又会随时间而改变，因此对于每一个样本工况，选取沿反应进程的 60 个时间点的数据进行简化计算.压力1 MPa、当量比Φ为1、温度1 000 K 时反应沿程选取的样本点如图2(b)所示.此外，在温度和压力变化较大的时段，样本点更为密集，这样能捕捉到更多反应进程的信息.

表1 丙烯机理简化样本工况Tab.1 Sample conditions of propene mechanism reduction

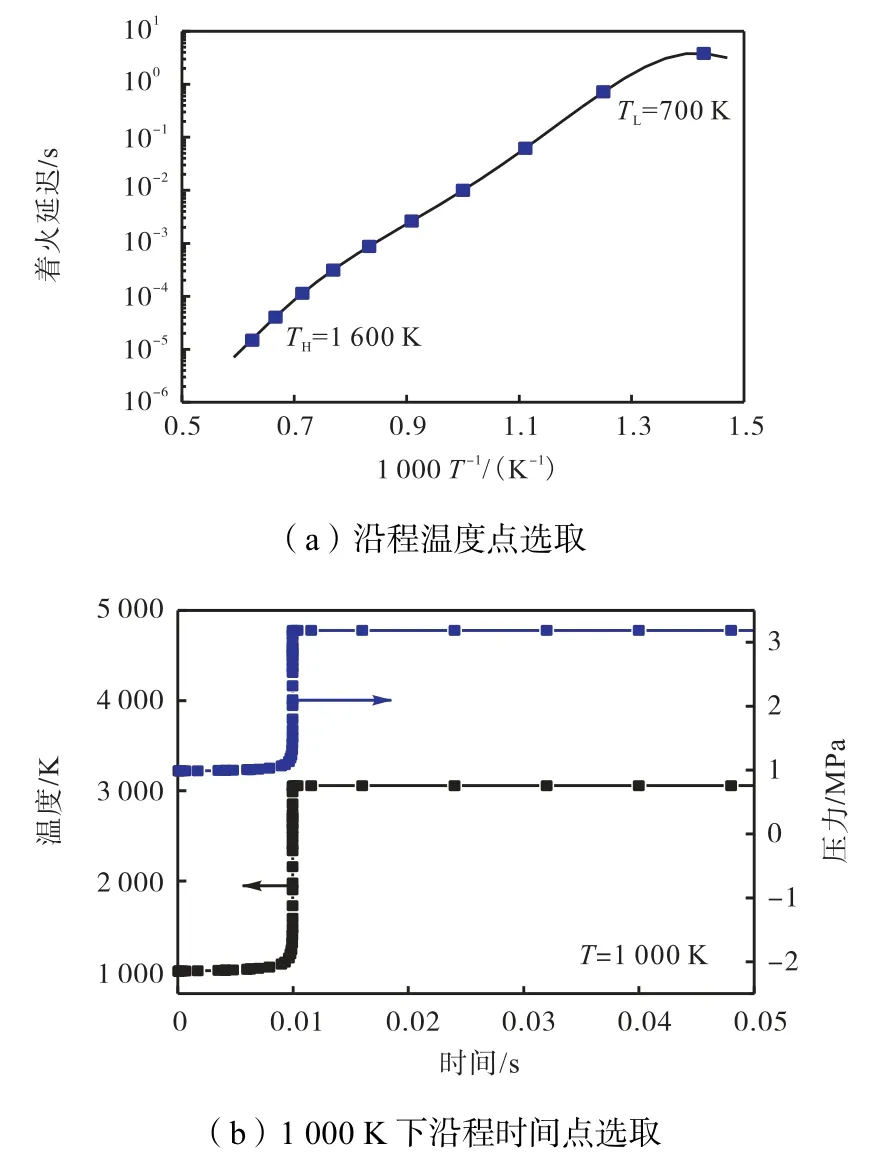
图2 p＝1 MPa，Φ＝1下简化样本点选取示意Fig.2 Schematic of selecting reduced sampling points at p＝1 MPa，Φ＝1

2.2 不同骨架简化方法比较

本文使用所构建的机理简化程序，对丙烯详细机理进行了简化，为了找出最优的丙烯简化机理，比较了4 种不同简化方法的简化效果，包括单步DRG 方法、单步DRGEP 方法、两步DRG 方法以及DRG 联合DRGEP 方法.简便起见，初始选取p＝1 MPa、Φ＝1、T 为700～1 600 K 的工况进行简化，设定简化机理精度为10%.不同阈值下，使用单步法获得的丙烯简化机理组分数变化和最大着火延迟误差曲线如图3 所示.

图3(a)为使用单步DRG 方法得到的不同阈值下骨架机理组分数以及样本点着火延迟计算的最大误差变化曲线，在对本文的样本点计算发现，随着阈值的增大，骨架机理组分数呈现线性减少，而着火延迟的误差随阈值的增大呈非线性的变化.当阈值小于0.11 时，误差一直保持在较小的值，而在阈值大于0.11 后，误差呈迅速上升趋势.在不超过设定误差的前提下，综合考虑骨架机理的规模与误差，选择一个全局最优的阈值来达到最优的简化效果.最终，基于10%的设定误差，选取阈值0.106，简化机理组分数203，反应数为1 187，最大误差为9.95%.

图3 单步法丙烯骨架机理组分数和着火延迟最大误差随阈值的变化Fig.3 Number of species and maximum error of ignition delay time prediction against different thresholds for propene skeletal mechanism generated by single-stage methods

图3(b)为使用单步DRGEP 方法得到的丙烯骨架机理组分数和最大误差随阈值的变化.由于考虑了距离长短对两组分之间相关性的影响，DRGEP 方法的阈值要小于DRG 方法的阈值.相比于DRG 方法，DRGEP 方法的组分数在简化初始阶段快速减少，当阈值大于0.035 时，组分减少的进程相对变缓，而着火延迟最大误差曲线也随阈值的增大呈非线性变化.值得一提的是，在阈值0.07 前出现了一个波谷，即当组分数进一步减少时，简化的骨架机理反而具有更高的精度.Tosatto 等[26]在对JP-8 航空煤油的简化中也发现了这种非线性变化现象.对该非线性的一个合理解释为：RAB是绝对值，仅体现组分之间生成或消耗的相关性大小，而不提供正负相关性信息.某些组分的去除可能使着火延迟增大，而在进一步减少组分时，组分的去除又会使着火延迟减小，这样总的着火延迟误差反而变小.因此，最大误差并不是严格地随阈值的增大而增大.最终，单步DRGEP方法下选取阈值为0.068，简化机理包含220 组分和1 253 个反应，最大误差为9.30%.

图4(a)、(b)分别为两步法中第二步使用DRG和DRGEP 方法进行简化的计算结果.两步法中，首先根据图3(a)中单步DRG 方法计算的误差曲线，选取第一步简化阈值为0.106，得到一个简化机理，再在新机理基础上进行第二次简化计算.由图可见，使用两步法进行简化时，误差开始随阈值变化不明显，而后有一个很明显的阶跃，说明此时有较多的耦合组分，进一步删除组分会带来很大的误差.此外，在本文对丙烯的简化过程中发现，第二步使用DRG 方法和DRGEP 方法的简化效果差异不明显，这可能是因为用于二次简化的机理规模已经较小，可简化的空间不大.考虑到10%的设定误差，对两步DRG 方法最终选取阈值0.1，简化机理组分数为189，最大误差为9.94%.同样地，对DRG 联合DRGEP 方法最终的阈值选取 0.175，简化机理组分 187，最大误差为9.94%.表2 列出了分别用四种方法得到的简化机理的相关信息.

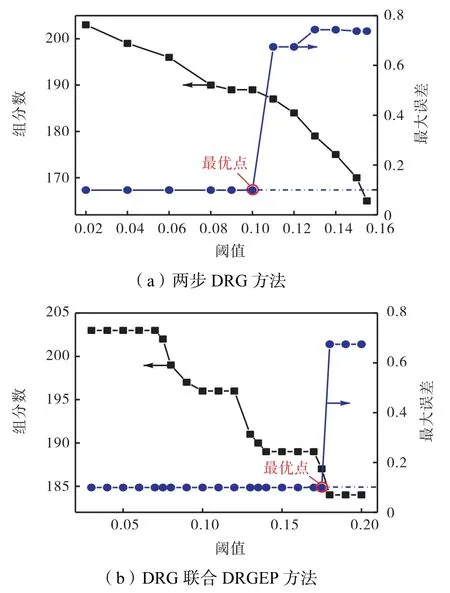
图4 两步法丙烯骨架机理组分数和着火延迟最大误差随阈值的变化Fig.4 Number of species and maximum error of ignition delay time prediction against different thresholds for propene skeletal mechanism generated by twostage methods

总的来说，基于DRG 的骨架简化方法均可以对原机理有很大程度上的简化，本例中当组分数减少50%时，最大误差也不超过0.5%.而当组分数继续减少到一定程度，最大误差会快速上升.这样的变化趋势在单步DRG 方法、两步DRG 方法以及DRG 联合DRGEP 方法中均有所体现.综合考虑，本文选择第四种方法，即DRG 联合DRGEP 算法进行全局工况下的机理简化.

表2 不同简化算法得到的简化机理大小以及最大误差Tab.2 Size of reduced mechanisms and the corresponding maximum errors obtained by using different reduction methods

2.3 丙烯全局简化机理构建

根据对不同简化方法的分析，最终使用DRG 联合DRGEP 方法分别对不同压力、当量比和温度下的样本工况进行简化，将每组得到的简化组分集取并集，构建全局简化机理.本文发现简化机理对压力和当量比具有较好的可拓展性.经过计算发现，上节中对p＝1 MPa，Φ＝1 下简化得到的丙烯骨架机理在全局工况中均有较好的适用性，除p＝1 MPa、Φ＝2、T＝700 K 一个样本工况外，其余所有简化工况下的最大误差都小于10%，各工况下的平均误差约为2%.这大大节约了计算机的计算成本.由此可知，机理对温度的敏感性大于对压力和当量比的敏感性，在对详细机理进行简化时，可以首先对某一压力、当量比的工况进行简化，再外推至全局简化点的验证，这样可以有效提高计算效率.最后，本文采用DRG 联合DRGEP 算法，将原机理简化掉约62%的组分数和58%的反应数，获得了一个包含187 种组分、1 139 个基元反应的丙烯骨架机理，用于最终的验证.

3 丙烯骨架机理的验证

3.1 着火特性

为了验证所得的丙烯骨架机理的有效性，本文计算了零维定容模型反应器中不同压力当量比下的着火延迟随温度的变化，并与详细机理的计算结果进行比较.图5(a)～(c)分别展示了在当量比为0.5、1.0、2.0 下骨架机理与详细机理的着火延迟随温度的变化趋势.由图可见，丙烯骨架机理在压力1～4 MPa，温度680～1 680 K，当量比0.5～2.0 的范围内，简化机理的计算点几乎和原始机理计算点完全重合，说明简化机理在各个工况下对丙烯的着火延迟均有较好的预测能力.

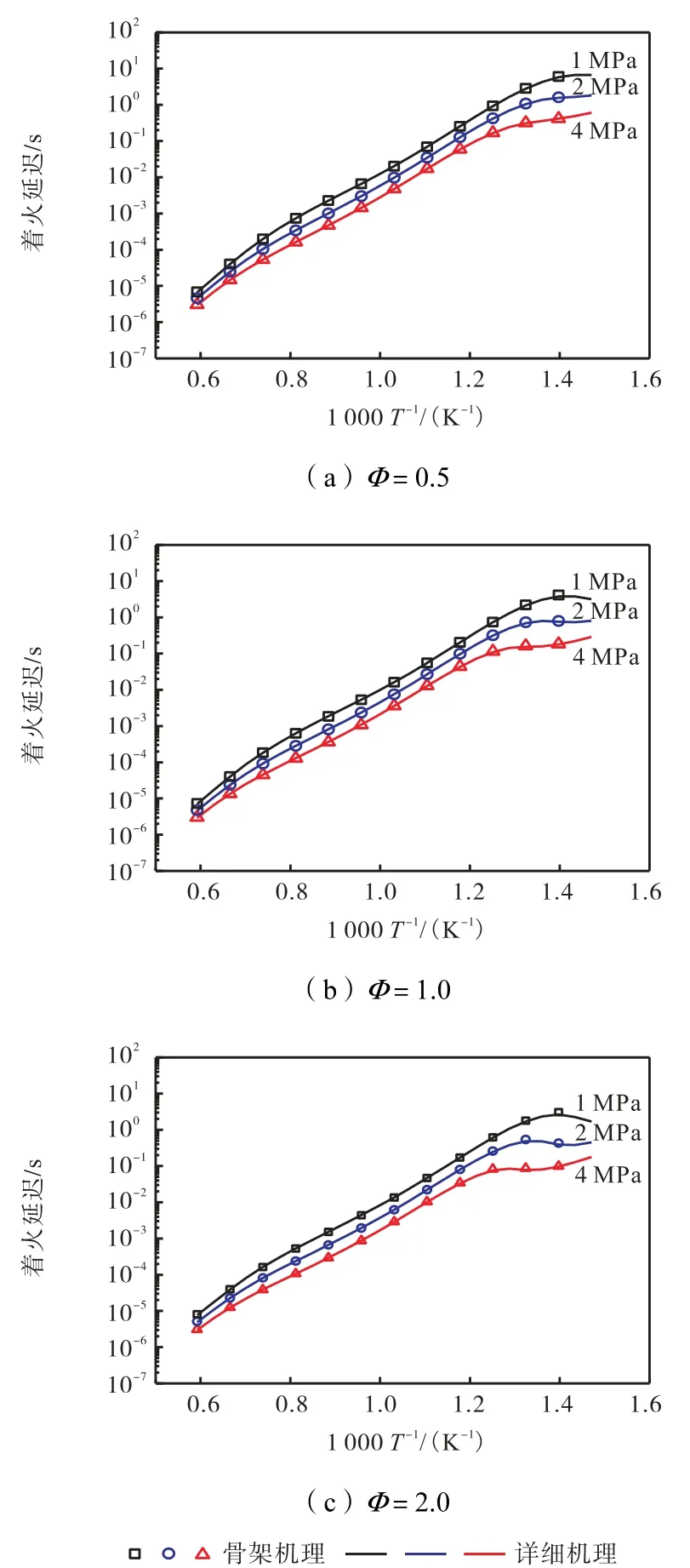
图5 不同工况下丙烯骨架机理与详细机理点火延迟比较Fig.5 Comparison of ignition delay time between propene skeletal mechanism and detailed mechanism in different working conditions

3.2 平推流反应器

为了进一步验证所构建的丙烯骨架机理的有效性，本文计算了等压绝热假设下的平推流反应器(LFR)模型中，丙烯详细机理与骨架机理对重要组分浓度随停留时间的变化(反应工况：p＝1 MPa，Φ＝1，初始摩尔分数0.33% C3H6、1.49% O2、98.18%N2)，并与Burke 等[25]在普林斯顿大学的变压流动反应器(variable pressure flow reactor，VPFR)上获得的实验结果进行比较，如图6 所示.为了更好地与实验数据进行对比，本文对详细机理与骨架机理的计算结果进行了 0.6 s 的时移[27]，以匹配丙烯燃料的消耗.从图中可以看出，骨架机理能够较好地预测丙烯氧化反应中组分的变化，且骨架机理与详细机理的计算结果比较吻合，仅在C2H4的预测上出现一些偏差.但计算结果仍然和实验结果存在一定偏离，表明详细机理还需要进一步修正.

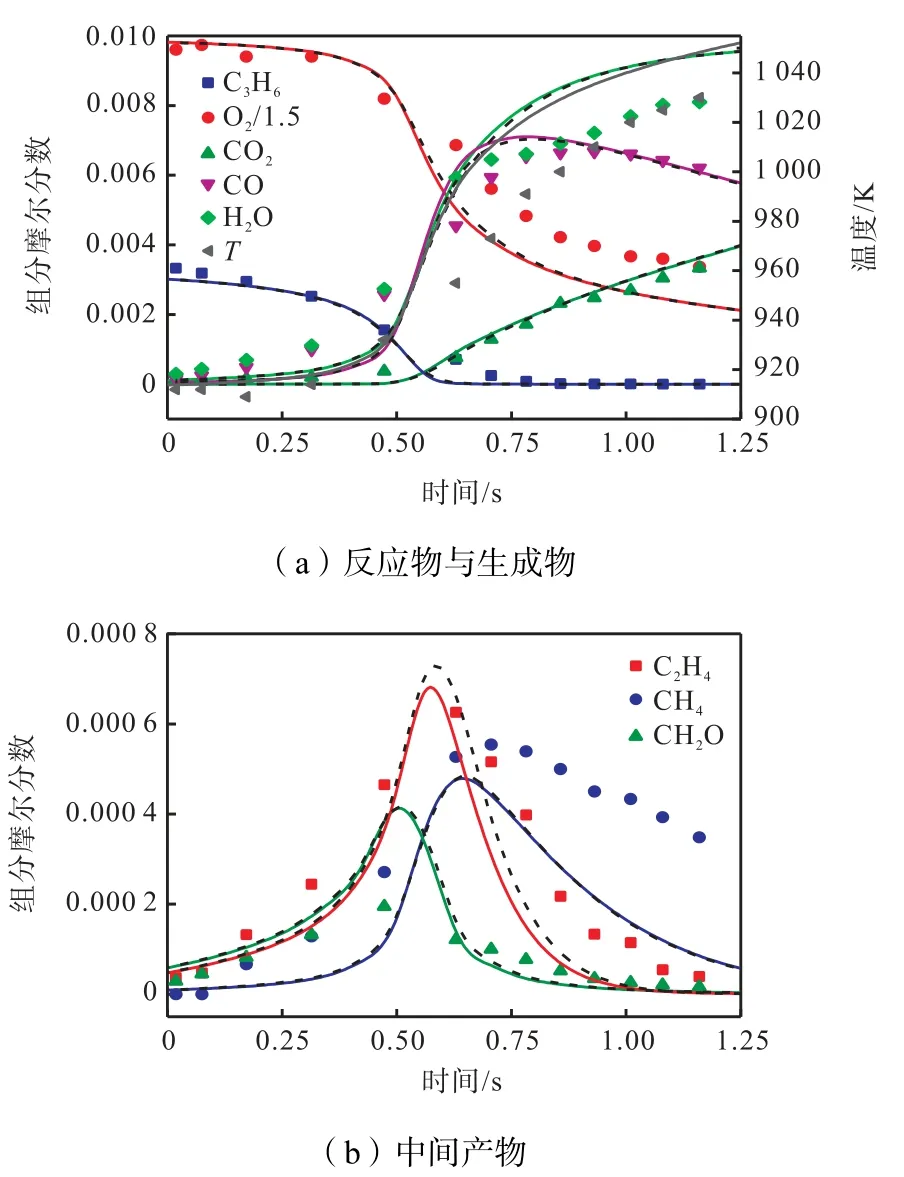
图6 丙烯骨架机理(虚线)和详细机理(实线)对LFR 模型中重要组分浓度变化的预测及实验数据(点)对比，p＝1 MPa，Φ＝1Fig.6 Comparison of mole fractions of major species in LFR model between predictions using propene skeletal mechanism(dashed line) and detailed mechanism(solid line) and experimental data at p＝1 MPa，Φ＝1

3.3 层流火焰速度

已有的研究[28]表明，机理中大分子的反应主要影响着火延迟，而小分子则更多地控制燃料的活化特性，决定燃料的火焰传播速度.也就是说，以着火延迟为简化目标获得的骨架机理并不能保证其对燃料的活化特性也有较好的预测.为了验证丙烯骨架机理在模拟火焰的输运特性时的可靠性，本文分别使用了丙烯详细/骨架机理进行不同压力下层流火焰速度的计算.初始温度T＝298 K，压力1～4 MPa 下不同稀释度的丙烯层流火焰速度如图7 所示，可以看到，简化机理与详细机理的模拟结果基本重合，说明本文发展的丙烯骨架机理对1-D 层流火焰速度有较好的再现性.

值得一提的是，燃料机理的规模直接决定了数值模拟的运算时间，在使用丙烯骨架机理计算层流火焰速度时，发现计算机的运算速度有明显提升.Lu 和Law[29]研究了计算机运算成本对机理的组分数之间的依赖关系，隐式求解的计算成本是机理包含的组分数的三次函数.由此可计算得，使用本文所发展的丙烯骨架机理进行1-D 层流火焰速度预测，所花的时间缩短至使用详细机理所花时间约1/18，大大节约了计算成本，有助于提高后续CFD 计算的效率.

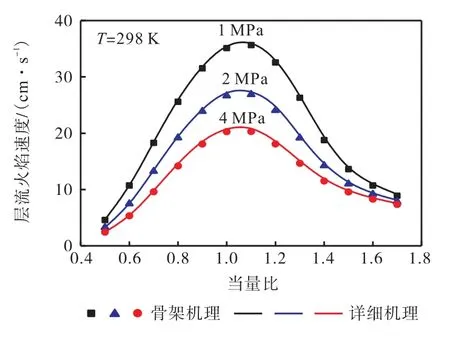
图7 不同压力下丙烯骨架机理与详细机理预测层流火焰速度随当量比变化的比较Fig.7 Comparison of changes in laminar flame speed with equivalence ratio predicted by using propene skeletal mechanism and detailed mechanism at different pressures

4 结论

(1)基于DRG 方法的骨架简化方法可以快速、有效地减小详细机理的规模.当组分减少50%时，最大着火延迟误差仅为0.5%.但当组分数减少到一定程度时，误差会出现阶跃.使用DRGEP 方法时，组分数在简化初始阶段减少得更快.两步法相比单步法在误差范围内可以进一步缩小机理规模，但可能由于丙烯详细机理规模较小，考虑运算成本后使用两步法的优势不明显.

(2)选用DRG 联合DRGEP 方法，基于p＝1 MPa，Φ＝1.0 工况下简化的丙烯骨架机理在全局范围内(680～1 680 K，1～4 MPa，Φ为0.5～2.0)均有较好的适用性，能有效减少运算成本.该机理在多个工况下的着火延迟均与原机理较吻合，对较高压力下层流火焰速度随当量比变化也有较为准确的预测效果，并且能较好地模拟丙烯在LFR 模型中重要组分浓度随停留时间的变化，这也进一步验证了本文所提出的机理简化方法的有效性与可行性.