三岔火焰及分层火焰的直接数值模拟分析
2019-12-24曾海翔李伟超陈明敏
曾海翔,王 平,余 倩,李伟超,陈明敏
(1.江苏大学能源与动力工程学院,镇江 212013;2.江苏大学能源研究院,镇江 212013;3.上海电气燃气轮机有限公司,上海 201199)
分层燃烧是一种当量比分布不均匀的燃烧方式,其优点之一是可扩大可燃混合物的燃烧极限[1].这一概念已经在实际燃烧器中实现[2].按照火焰的传播方式可将分层火焰分为“焰前支持”(front-supported)火焰和“焰后支持”(back-supported)火焰.“焰前支持”火焰,即火焰的传播方向由稀预混分支向浓预混分支蔓延;“焰后支持”火焰的传播规律则恰好相反,即火焰由浓预混分支向稀预混分支发展.而按照当量比变化进行分类,当量比介于富燃极限和贫燃极限之间时,仅能发生预混燃烧;一旦超过可燃极限,火焰中会同时存在预混和扩散两种燃烧方式,此时的分层燃烧又称为部分预混燃烧[3].
在燃料/空气混合层中传播的火焰,当燃料浓度梯度不均匀分布时,便会出现三岔火焰结构[4].三岔火焰作为一种典型的分层燃烧火焰,兼具稀预混燃烧、浓预混燃烧和扩散燃烧3 种燃烧模式.浓预混分支剩余的燃料和稀预混分支剩余的氧化剂扩散到中间,形成扩散火焰,扩散火焰分支中混合物接近化学平衡[5].三岔火焰广泛存在于多种流场条件下,例如协同流、自由射流和对冲流等.不同流场和燃烧装置下形成的三岔火焰具有两种形式,对冲流下平行三岔火焰和协同流下分叉型三岔火焰.分叉型三岔火焰3个火焰分支汇聚于化学当量比为1 的三岔点上.
研究三岔火焰对了解非稳态火焰的燃烧特性如着火、发展以及熄灭机制有很大帮助.自从1965 年Phillips 发现三岔火焰现象以来[6],国内外学者对三岔火焰产生了浓厚的兴趣.由于部分预混火焰具有多反应区的特征,数值模拟中经常采用的总包反应机理难以描述其火焰结构,因而大多数学者在计算过程中会选择较为详细的化学反应机理,Qin 等[7]针对重力对甲烷/空气部分预混层流火焰的影响开展了研究,计算过程中采用81 步甲烷反应机理;Yamamoto等[8]使用25 步甲烷化学反应机理来研究甲烷/空气共流射流下三岔火焰形态;Yuan 等[9]分析流场的壁面对甲烷/空气三岔火焰传播与几何结构特性的影响,其中的数值计算部分采用了甲烷184 步化学反应机理,对应的计算精度有一定提升,但其计算量也大大增加.
近些年来国内外同时针对甲烷发展了大量的化学反应机理.Hughes 等[10]通过对甲烷反应的动力学特性的测量,提出一套包含37 种组分351 个正向反应的甲烷详细化学反应机理,反应的详细参数以CHEMKIN 格式置于网上.Slavinskaya 等[11]基于敏感性分析的方法将烃类化学动力学数据库中C0~C1氧化的一般动力学方案进行推广,得到一套低压甲烷燃烧的骨架反应机理,并通过着火延迟和层流火焰速度对比对其进行了评估.Novosselov 等[12]为预测工业燃气轮机的污染排放特性开发一套八步反应的甲烷总包反应机理,相较之前提出的五步反应机理进一步增加了压力梯度的适应范围.刘合等[13]在研究甲烷/空气预混超声速燃烧时提出一套包含14 种组分18 个基元反应的简化机理,该机理在预测点火延迟方面具有较高精度且在高、低压力范围内均表现良好.胡贤忠等[14]基于GRI 3.0 详细机理构建了甲烷在O2/CO2气氛下燃烧的框架机理和总包机理,为甲烷在O2/CO2气氛下的燃烧过程的数值模拟提供高效的简化模型.
为了降低计算成本的同时有效提高计算精度,在过去几十年中已经开发了多种简化动力学方法,主要有计算奇异(CSP)方法[15]、自适应建表(ISAT)方法[16]和固有低维流形(ILDM)方法[17].其中ILDM 方法是基于对化学系统非线性响应动态行为的直接数值分析,通过对化学反应项的Jacobian 矩阵进行特征值分析,把反应空间分解为快反应子空间和慢反应子空间.在慢反应子空间中构造流形,从而实现用部分参数来表征整个化学系统的组成.ILDM 方法在简化机理的过程中假设化学反应占主导地位,忽略了低温区对流扩散对化学反应造成的影响.因此,只在高温区有很好的模拟精度.增加子空间维度是提高低温区的计算精度的方法之一,但同时极大地增加了计算量.由van Oijen 等[18]提出的火焰面生成流形(FGM)和Gicquel 等[19]提出的火焰固有流形延伸(PFI)方法,正是基于ILDM 方法并考虑了扩散效应,得到了广泛的应用.这两种方法成功应用于预混和扩散燃烧的数值模拟后,越来越多的学者尝试将其用于部分预混火焰.Fiorina 等[20]将二维PFI 表格应用于部分预混火焰,发现当混合物当量比位于可燃界限内时,PFI 模型获得优良结果;反之,出现FPI 结果与详细化学反应机理结果的偏离.Wu 等[5]在计算二维三岔火焰时,发现FPI 制表模型预测的CO 质量分数远大于详细反应机理下的结果.宋帅[21]通过引入火焰指数将FGM 预混表和FGM 扩散表应用于部分预混火焰,得到了较好的结果,但计算量有所增加.Steinhilber 和Maas[22]发展的“Reaction-Diffusion Mainfold”方法则较好地克服了计算量上升这个问题.王蔡军等[23]利用二维REDIM 表结合假定概率密度函数(PFDF)对Darmstadt 大学分层燃烧装置进行了计算,与实验结果吻合很好,但计算所设置的混合物当量比均在可燃界限内.
为了研究不同当量比条件下三岔火焰及分层火焰的燃烧特性,同时验证二维REDIM 表格对部分超出可燃极限燃烧状态的描述能力,本文考虑了4 种不同当量比布局的层流火焰,并采用详细甲烷化学反应对其进行计算.计算稳定后,对比分析了这4 种火焰的火焰结构及火焰面上的燃烧状态,并将计算域内每个网格点的N2和CO2值投影到二维REDIM 表格中,观察REDIM 表格是否完全容纳投影的结果.
1 反应-扩散流形方法
REDIM 方法在生成低维流形时同样考虑了化学反应对分子输运过程的影响,并引入不变流形理论.最终得到的低维流形方程[24]如式(1)所示:
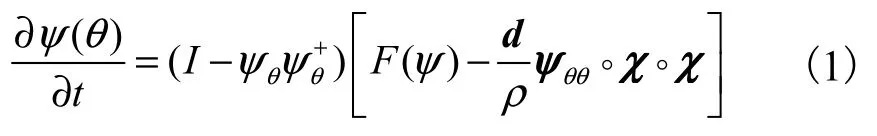
式中:ρ为密度;χ=grad(θ)为θ的空间梯度矢量为Hessian 矩阵;d 为分子扩散系数矩阵,符号“◦”为具有三阶张量的矢量运算.REDIM 表格的生成方法可以分为以下几个步骤[22]:
(1) 指定方程(1)初始条件和边界条件;
(2) 将梯度grad(θ)指定为θ的函数;
(3) 对方程(1)进行时间积分,直到达到稳定状态;
本文中采用Dirichlet 边界条件,通过INSFLA[25]程序使用详细化学反应机理求解不同一维层流小火焰单元,继而生成REDIM 表格的计算边界和初始流形.这些小火焰单元包括Air-CH4冷态的纯混合流、Air-pilot 对冲火焰和fuel-pilot 对冲火焰等.如图1(a)所示,红色线条表示fuel-pilot 对冲火焰,绿色线条表示pilot-Air 对冲火焰,底部蓝色线条表示Air-CH4对冲流中无燃烧的纯混合过程,这3 条线构成二维REDIM 表格的边界.边界内部的虚线表示不同拉伸率下的fuel-Air 对冲火焰,用于指定REDIM 表的初始流型.曲线从上到下表示拉伸率从小到大,当拉伸率过大时,火焰会呈现熄火状态,初始流型只要在计算边界内均可用于REDIM 表的计算.图1(b)表示的是由N2-CO2-OH 所表示的三维骨架图,图中绿色的虚线表示瞬间熄火的小火焰单元.由此可见二维REDIM 表格能够描述熄火状态,比较适用于计算部分预混火焰.将所计算的小火焰单元 Profilecounterdiff 文件中最后一个DATA 数据导入REDIM表格生成程序中,指定方程的初始条件和边界条件,得到如图1(c)所示的初始流形.
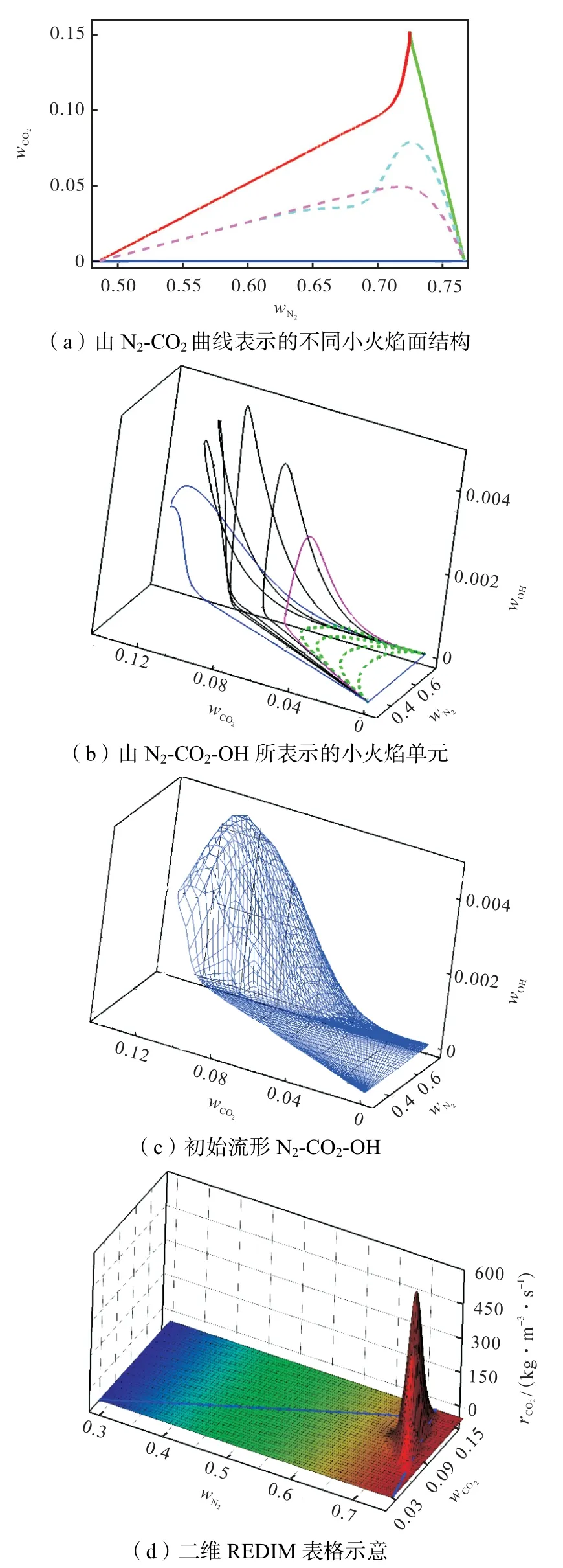
图1 二维REDIM表格生成过程示意Fig.1 Schematic of generation of 2D REDIM table
通过执行步骤(2)、(3)和(4),最终得到以N2和CO2质量分数为自变量的二维REDIM 查询表,如图1(d)所示表征反应进程,wN2表征混合过程,表示CO2生成速率.其他热力学变量信息可以通过二维REDIM 表查询得到.无燃烧的混合过程中CO2的质量分数为零;N2的质量分数可以反映混合气的混合状态,纯空气流对应N2质量分数取最大,而当量比达到最大值时,此时的 N2质量分数最小.根据其物理意义,这两个组分的质量分数主要集中在图1(d)所示的三角形范围内.
2 计算设置
2.1 边界条件设定
本文一共计算了4 种状态下的火焰,如图2 所示,其中状态A 和B 两种分层火焰,混合气当量比分别超出可燃上限和可燃下限.由当量比等于1 的甲烷/空气混合物燃烧后的高温废气分别点燃当量比在富燃区间(状态A)和贫燃区间(状态B)线性变化的新鲜混合气体,废气的入口速度为0.5 m/s,新鲜混合气入口速度为1 m/s.其中,状态A 为“焰前支持”火焰,预混气体位于5 mm<y≤15 mm 处,混合气当量比从1 到2 线性增加;状态B 为“焰后支持”火焰,预混气体位于5 mm<y≤15 mm 处,混合气当量比从1~0 线性减小.状态C 和D 是两种特殊的分层火焰,具有典型的三岔火焰结构,混合气入口温度为300 K,计算域的内部为高温燃烧废气.状态C 的入口混合气的速度为0.5 m/s,当量比从0~2 线性增加,y=7.5 mm 处当量比为1;状态D 的入口混合气的速度为0.4 m/s,当量比从0.5~1.5 线性增加,y=7.5 mm 处当量比为1.除了入口条件的设置不同,这4 个状态的火焰具有相同的计算条件.其中壁面采用滑移边界条件;压力出口设置为常压,p=101 325 Pa.所有计算采用15 mm×25 mm 的二维矩形计算域,在x 和y 方向分别均匀设置600 和1 000 个网格单元,网格尺寸为25 μm,足够求解火焰结构.
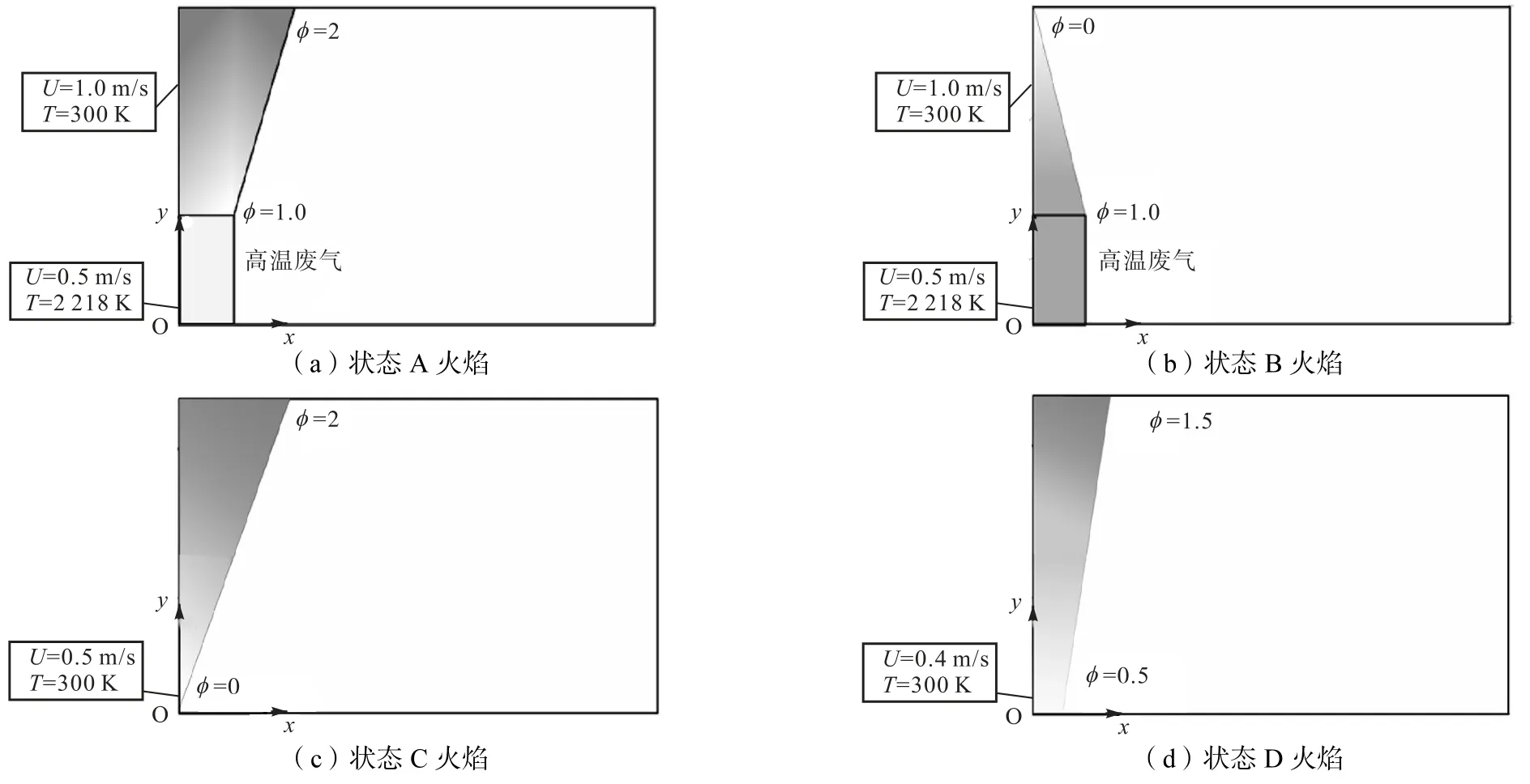
图2 4个层流火焰的计算域及边界条件示意Fig.2 Schematic of calculation domain and boundary conditions of four laminar flames
2.2 计算方法
本文计算基于 OpenFOAM 开源软件,选用rhoReactingBuoyantFoam 作为求解器.计算过程中采用甲烷-空气详细反应机理[26],对控制方程中的时间项采用了默认的一阶隐式Euler 差分格式,对流项采用限制差分型TVD 格式,扩散项采用二阶线性修正高斯差分格式.在OpenFOAM 中可以通过库朗数自动调整时间步长,这里取为0.4,计算过程中迭代误差统一设置为1×10-9.
3 结果分析
3.1 火焰结构分析
为了区分燃烧过程中的预混和扩散区域,以进一步判断当地的燃烧机制,Yamashita 等[27]提出了火焰指数的概念,火焰指数定义为


图3 状态A温度、当量比、CO2生成速率以及火焰指数示意Fig.3 Skematic of temperature,equivalence ratio,formation rate of CO2,and flame index in state A

图4 状态B温度、当量比、CO2生成速率以及火焰指数示意Fig.4 Skematic of temperature,equivalence ratio,formation rate of CO2,and flame index in state B
图3 和图4 分别展示了两种分层火焰下的温度(T)、CO2生成速率(rCO2)、当量比(φ)和火焰指数云图.对比图3、图4 发现,两种分层火焰状态只有一个火焰分支,且火焰面的位置基本一致.通过CO2的生成来反映火焰面的位置,由火焰面处的火焰指数发现:状态A 和状态B 火焰面处火焰指数都接近1,因此这两种燃烧模式下的火焰均为预混火焰主导.虽然入口反应物浓度范围分别为[0,1]和[1,2],均部分超出可燃极限,但并未产生扩散火焰分支.由当量比分布云图知,状态A 和状态B 中计算域内混合物当量比呈现分层分布现象,符合入口混合物的当量比设置.
图5 和图6 中OH 质量分数分布云图清晰地展现了状态C 和状态D 中的3 个火焰分支.结合图5、6 中的CO2生成速率rCO2云图可知,在这两个状态下两侧的火焰分支均为预混火焰,中间的火焰分支为扩散火焰.浓预混火焰分支位于扩散火焰分支的上方,稀预混火焰分支位于扩散火焰分支的下方.同时发现,在三岔点上和扩散火焰分支处OH 质量分数远高于两个预混火焰分支,稀预混火焰分支处OH 质量分数稍高于浓预混火焰分支.状态C 混合物入口浓度梯度大于状态D,由CO2生成速率图可知:状态C 三岔火焰扩散火焰分支相较于状态D 更加清晰,与文献[28]中所提及浓度梯度增加,扩散火焰分支逐渐增强这一结论相符.状态C 混合气入口速度为0.5 m/s,在计算中火焰能够稳定在某一位置;对状态D 设置相同的入口速度时,发现火焰不停地向下游传播,直至离开计算域;将预混气的入流速度设置为0.4 m/s时,火焰驻定在计算域中,但稳定高度距离入口约8 mm 处,高于状态C 的3.7 mm 举升高度.由此认为状态C 三岔火焰的传播速度大于状态D.状态C 和状态D 的火焰传播速度均高于均匀预混条件下的层流火焰的传播速度(约为0.3 m/s),考虑到状态C 的预混气体的浓度梯度高于状态D,可以判断在均匀浓度梯度分布的条件下,增大预混气的浓度梯度有助于火焰的传播,同时火焰的举升高度也发生显著的降低.

图5 状态C温度、CO2生成速率、OH质量分数以及火焰指数示意Fig.5 Skematic of temperature,formation rate of CO2,OH mass fraction,and flame index in state C
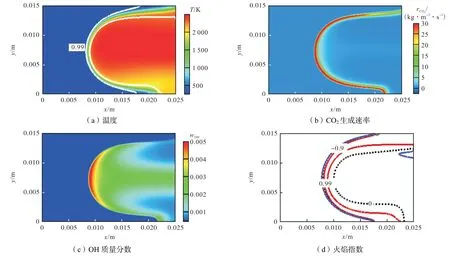
图6 状态D温度、CO2生成速率、OH质量分数以及火焰指数示意Fig.6 Skematic of temperature,formation rate of CO2,OH mass fraction,and flame index in state D
结合4种状态下火焰指数分布图发现,对于简单的预混和扩散火焰,火焰指数能够很好地用来判断当地的燃烧模式,如状态A 和状态B 两种火焰的火焰面处均只存在一个火焰指数0.9,这表明此时状态A和状态B 火焰面上的燃料和氧化剂的位移夹角非常小(约为3°以内).而对于本文中的三岔火焰状态C和状态D,结合OH 基生成云图,可以清晰地看见此时上下两端的预混火焰分支和中间的扩散火焰分支于y=7.5 mm 附近的三岔点处相遇,对应化学当量比等于1.此时,该点处的燃烧模式既不属于预混火焰,也不属于扩散火焰.然而在图5 和图6 火焰指数分布示意图中,位于三岔点的火焰指数显示为0.99.根据火焰指数定义,此处的燃烧模式应该为预混燃烧主导.这与该点的实际燃烧模式不符,故此火焰指数的表达式在三岔点处不尽合理,有必要进一步完善.
3.2 计算域内N2、CO2质量分数散点图分析
本文生成的二维REDIM 表格选取的参考变量为N2和CO2的质量分数,在燃烧数值模拟中可以通过查找上述参考变量来确定对应状态下其他变量的信息,有效规避了详细求解复杂的化学反应.在制表过程中,当量比选取的范围在0~10 之间,涵盖了本文中4 种状态所设置的当量比分布.如图7~图10所示,蓝色线条表示由二维REDIM 表格生成的计算边界,假如REDIM 表格可以很好地反映火焰的详细信息,则实际的火焰信息通过查表法转换的散点应该全部被容纳在计算边界内,即图中的蓝色线条封闭的区域内.为了加以验证,将上述4 种火焰计算域内各点的N2和CO2质量分数值投影到二维REDIM 表格中,观察这些点的分布情况.从图7 和图8 中不难看出,状态A 和状态B 散点图中N2质量分数呈现出沿化学当量比下N2质量分数wN2=0.725 这条竖线的对称分布,这正好符合状态A 和状态B 火焰入口处的梯度设置(状态A 的当量比范围1~2,状态B 的当量比范围0~1).图9 中状态C(当量比0~2)散点图中N2质量分数分布最广,说明此状态下火焰内部的当量比分布最广.状态D(当量比0.5~1.5)散点图中N2质量分数分布较状态C 稍窄,但这两种状态当量比分布都显示出火焰从贫燃区跨度到富燃区,验证了浓度梯度不均匀分布的分层燃烧技术可以有效扩大可燃物的燃烧极限.
4 种状态N2和CO2质量分数对应点都落在二维REDIM 表格中,说明4 种状态下的计算域内各网格点对应的热化学参数都能被此二维REDIM 表格求解,图7~10 可以比较直观地说明二维REDIM 表格适用于部分预混火焰.后期将采用二维REDIM 表格计算本研究中四种状态火焰,并与GRI3.0 机理的结果进行对比,详细分析二维REDIM 表格的适用性.

图7 状态A火焰散点图分布Fig.7 Scatter plot in state A
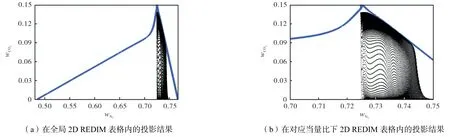
图8 状态B火焰散点图分布Fig.8 Scatter plot in state B
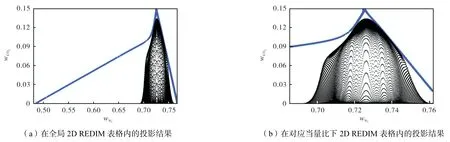
图9 状态C火焰散点图分布Fig.9 Scatter plot in state C
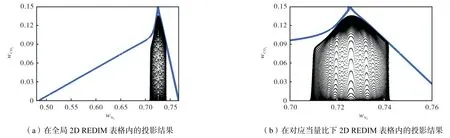
图10 状态D火焰散点图分布Fig.10 Scatter plot in state D
4 结论
本文通过4 种层流火焰的直接数值模拟计算,对火焰结构进行分析,并将计算域内各点N2和CO2质量分数投影到二维REDIM 表格中检验其适用性.研究表明:
(1) 虽然两种分层燃烧状态A 和状态B 混合物入口处的当量比范围均超出可燃界限,但均只存在一个预混火焰分支;状态C 和状态D 则呈现出三岔火焰结构.
(2) 通过计算火焰指数,发现该火焰指数能很好地表征预混或扩散火焰的火焰状态,对于复杂的部分预混火焰,如三岔火焰,则存在一定的缺陷.
(3) 将计算域内各网格点的热力学状态投影到二维REDIM 表格中,发现4 种状态计算域内各点N2和CO2质量分数散点都落在二维REDIM 表格内,这表明本文生成的REDIM 表格可扩展到部分预混火焰的研究中,为此类问题的研究提供一个可能的解决方案.
