河南省渔业生产数据的方差分析
2019-12-23陆宜清张新育
陆宜清,张新育
(1.河南牧业经济学院,河南 郑州 450046; 2.郑州大学,河南 郑州 450001)
河南是人口大省,也是农业大省,农业的发展影响着全省人民生活的质量水平。随着渔业不断的发展壮大,其发展成效显著,渔业已经成为全省农业和农村经济中的重要组成部分。2017年渔业生产近130万吨,渔业经济总产值261.54亿元,全省渔民人均纯收入达13733元。
河南省自北向南跨海河、黄河、淮河、长江等四大流域。气候属亚热带向暖温带过度区域,既有北方的特点,又保留了南方的特征,适合多种鱼类的生存,有黄河鲤鱼、黄河鲶鱼、光山青虾等名贵的水产种质资源。具有十分便利的交通网络,省会郑州作为全国重要的交通枢纽,是连接南方和北方的纽带。
随着人口的增长和生活水平的提高,膳食结构的改善以及城镇化趋势的加快,水产品的需求将稳步增长。为了应对水产市场的短缺,河南省应该加强渔业的发展,进一步推动农村经济的发展。针对不同地市的渔业发展,如何分配现有的水产以及地势资源,使河南省的渔业大力的发展,更好地应对水产市场的短缺情况,提高人民的生活水平显得非常重要。
本文的研究目的是,对不同地区、时间和种类这三个因素对河南省渔业产量增长的稳定性进行探讨并总结,主要考察的指标为增长率。通过对影响稳定性的三个因素的探讨,来改善河南省渔业养殖的地区分配,尽量运用各个地区的优势去养殖水产品。
1 研究方法及原理
在渔业生产中,渔业的总产量受到地区、时间和类别等因素的影响,在这些因素中,有的影响显著,有的影响不显著,方差分析是鉴别各因素影响程度的一种有效统计方法。为了鉴别三种因素对总产量的影响,采用双因素方差分析的统计方法,分别对三个因素两两进行分析。
设有两个因素A,B,因素A有p个水平A1,……,Ap,因素B有q个水平B1,……,Bq,对因素A,B的每一搭配(AiBj),i=1,……p,j=1,……q,作r次试验,得到数据结果。
其数学模型为
Xijk=μ+αi+βj+δij+εijk
i=1,……,p,j=1,……,q,k=1,……,r,假设这些数据是相互独立的,则有Xijk~N(μij,σ2),Xijk与μij的差值可以看成一个随机误差εijk,假定εijk~N(0,σ2)且彼此独立。
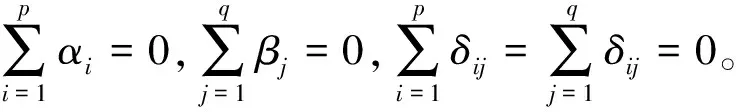
效应αi,βj和δij估计分别为
其中
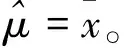
要检验各因素及他们之间各种交互作用是否显著的假设为
H01:αi=0 ,一切iH11:至少有一个i,αi≠0
H02:βj=0,一切jH12:至少有一个j,βj≠0
H03:δij=0,一切i,jH13:至少有一对i、j,δij≠0
要建立对上述假设的检验统计量,需要先计算以下平方和:
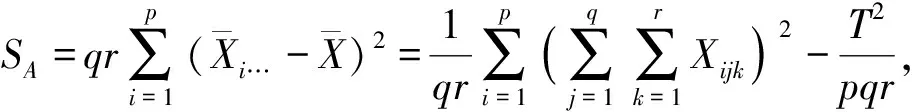
其平方和分解公式为
Sr=SA+SB+SC+SA×B+SE
方差分析表为

表1 两因素方差分析表
对于给定的显著性水平α,可由F分布表查得所需的临界值。拒绝域分别为FA≥Fα[p-1,pq(r-1)],FB≥Fα[q-1,pq(r-1)],
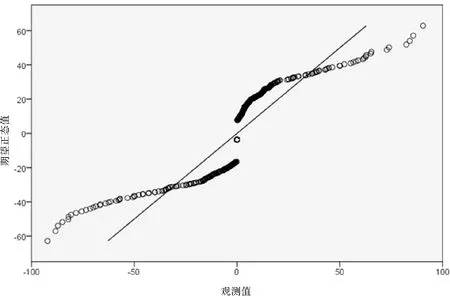
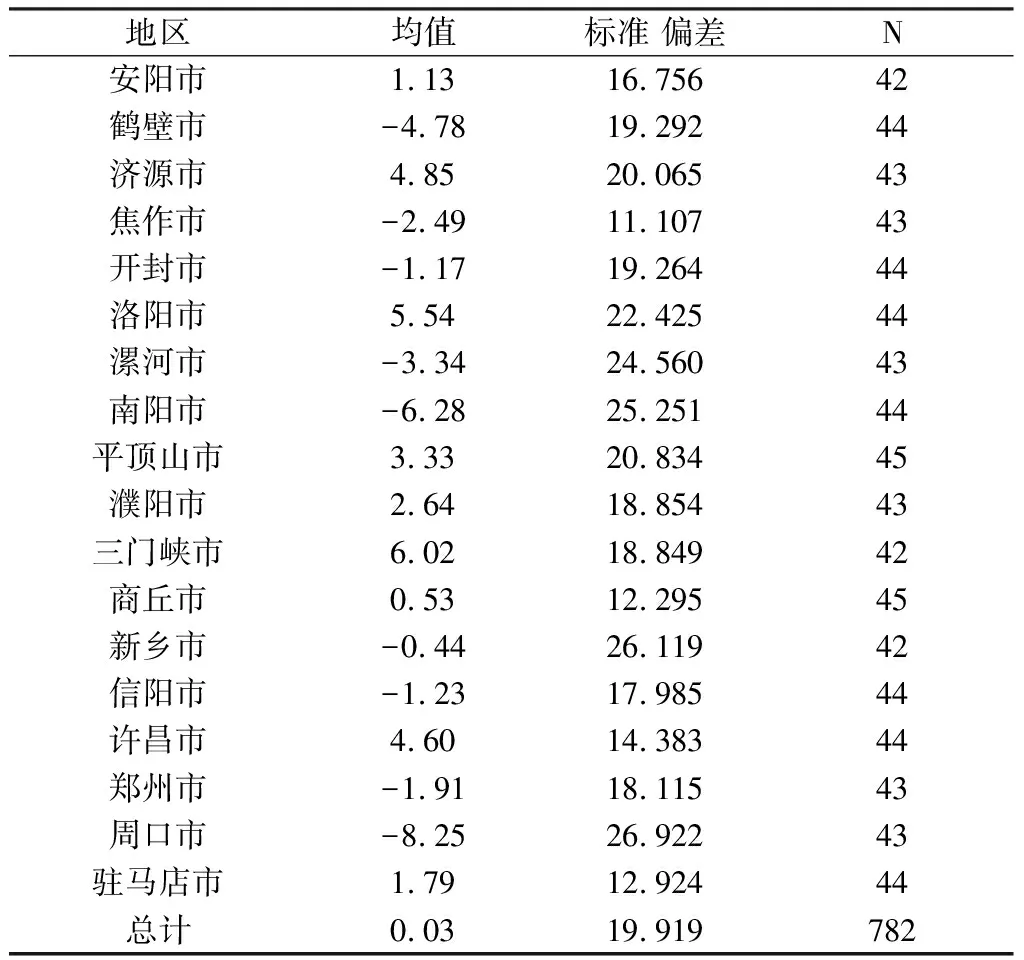
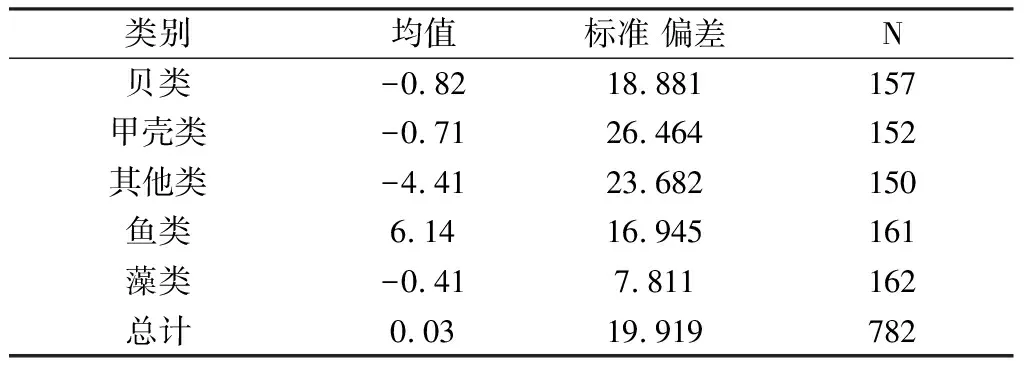
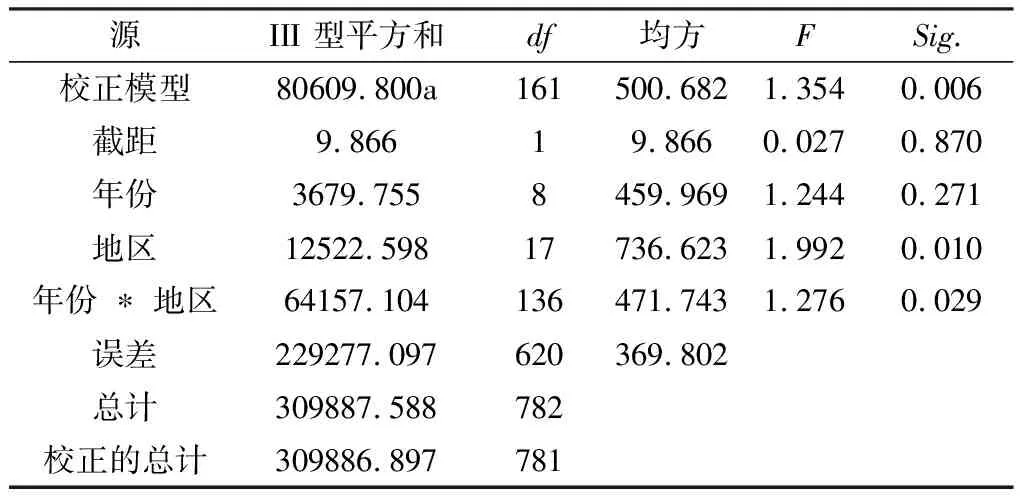
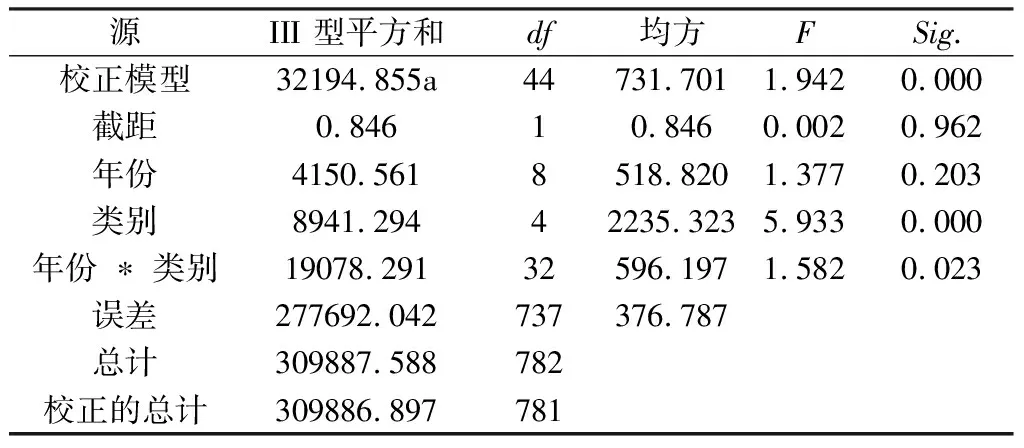
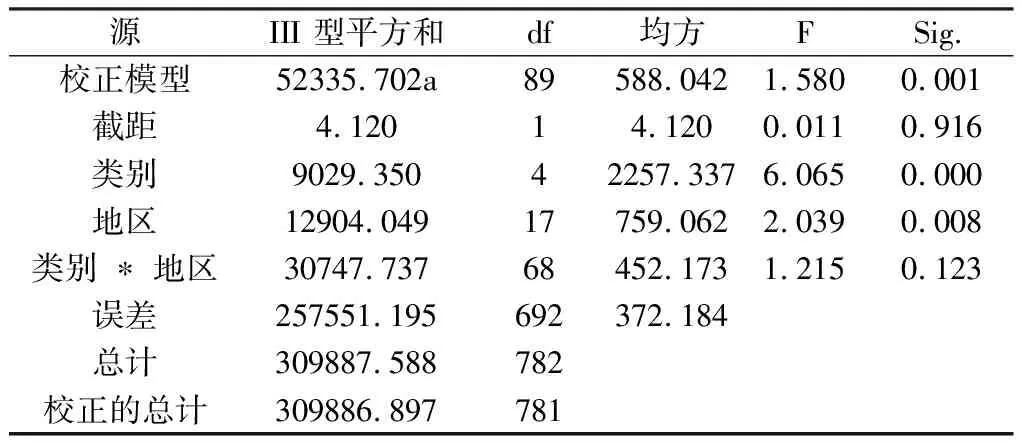
FA×B≥Fα[(p-1)(q-1),pq(r-1)],当所求得F值落入拒绝域内时,则拒绝原假设,认为该因素的作用显著。例如Fa((p-1)(q-1),pq(r-1)),如果FA×B>Fα((p-1)(q-1),pq(r-1)),则拒绝H03,即可认为因素A与因素B的交互作用是显著的。 也可以用p值进行判断,用软件得出p值,将其与显著性水平α作比较。当α≥p时,则在显著性水平α下拒绝H0,如果α 使用两因素方差对这三个因素进行分析处理时,需要考虑如下假设: 假设1:因变量唯一,且为连续变量,相互独立; 假设2:有三个因素,每个因素有2个或以上的水平; 假设3:对于因素的各个水平,因变量需近似服从正态分布; 假设4:对于因素的各个水平组合产量的误差εijk,近似服从正态分布。 2.2.1 异常值检验 为了使方差分析能够得到更好的检验结果,对增长率这一变量进行异常值检验。在箱线图中,把超过四分位差1.5倍距离的数值定义为离群点,在图中用“o”表示;把超过四分位差3倍距离的数值定义为极端值,用“*”表示。用SPSS软件将增长率按各个类别作箱线图如下: 由得出的箱线图可知,存在大量的极端值点。为了验证这些极端值的来源,去查原始的数据表,得到这些极端值是真实存在的增长率。由于各类水产品每年产量波动较大,大部分地区养殖的品种主要是鱼类,也有少数地区养殖藻类和其他类产品,其中引入了新的水产品,并且前一年养殖效果良好故下一年大量引入,所以增长率过高而成为异常值。例如图中1500%的增长率,查数据表可知它是2016年洛阳市贝类针对前一年的增长率,2015年产量为5吨,而2016年产量为80吨,故由增长率的公式算得为1500%。虽然对于真实存在的极端值我们没有理由将其当作无效值,但由于我们的样本量足够大,为了后面检验的有效性,我们将增长率控制在(-1,1)内,剔除区间外的增长率。 2.2.2 假设检验 对于以上的假设,此处的数据因变量仅为增长率,且为连续变量并相互独立。三个因素分别为年份、地区和种类,年份为2009-2017共9个水平,地区为各个地市共18个水平,种类有5个水平。可知假设1和假设2成立。 图1 增长率(%)的线箱图 图2 增长率(%)的正态Q-Q图 由上述的正态概率图,可知因变量增长率稍微偏离正态标准线,因此该因变量不近似服从正态分布,也说明了该数据不能用多元正态模型进行处理。而由于方差分析对于偏离正态分布比较稳健,且样本量较大,对于偏态的分布,可采用方差分析的统计分析方法对数据进行处理。 统计分析的目的是研究数据的总体特征,而描述性统计分析也是统计分析学中的基础,是对分析数据进行正确统计推断的先决条件。通过描述性统计分析,可以使杂乱无章的数据呈现出规律性,为数据建模提供依据。故对该数据进行描述性统计分析,得到关于产量均值与标准差的统计值如下: 2.3.1 年份的描述性统计分析 如下表2所示,随着时间的变化,每年产量的增长率是不断变化的。其中2011年、2012年和2013年的增长率为负值,其余年相对于前一年的增长率均为正值。且每年相对于前一年变化的幅度不尽相同,2013年的增长幅度最大为4.10%,2011年的增长幅度仅为0.76%,相对稳定。 表2 年份的描述性统计量因变量:增长率(%) 年份均值标准偏差N2009-1.5326.239852010-1.4119.4698520110.7622.4858720123.9324.4788720134.1019.018862014-1.0916.898882015-1.8714.483882016-0.8217.386892017-1.7715.55987总计0.0319.919782 2.3.2 地区的描述性统计分析 由表3可得,每个地区的产量增长率都存在差异。其中增长率呈负数的地区有焦作、开封、鹤壁、漯河、南阳、新乡、信阳、郑州、周口,其余9个地区的增长率呈正值。增长幅度最大的是周口市,为-8.25%,最小的是新乡市,为-0.44%。 表3 地区的描述性统计量因变量:增长率(%) 地区均值标准 偏差N安阳市1.1316.75642鹤壁市-4.7819.29244济源市4.8520.06543焦作市-2.4911.10743开封市-1.1719.26444洛阳市5.5422.42544漯河市-3.3424.56043南阳市-6.2825.25144平顶山市3.3320.83445濮阳市2.6418.85443三门峡市6.0218.84942商丘市0.5312.29545新乡市-0.4426.11942信阳市-1.2317.98544许昌市4.6014.38344郑州市-1.9118.11543周口市-8.2526.92243驻马店市1.7912.92444总计0.0319.919782 2.3.3 类别的描述性统计分析 由表4可得出,在5个类别的水产品中,鱼类的增长率最高为6.14%,由原始数据表可知鱼类是养殖产量最多的一类。产量除了鱼类其余类的增长值均为负值,但增长幅度较小,说明各种类养殖量的波动较小,相对较稳定。 表4 类别的描述性统计量因变量:增长率(%) 类别均值标准 偏差N贝类-0.8218.881157甲壳类-0.7126.464152其他类-4.4123.682150鱼类6.1416.945161藻类-0.417.811162总计0.0319.919782 由上述描述性统计分析可知,水产品的产量与年份、地区和种类有一定的相关性。为了更进一步的了解三个因素以及之间的交互作用对产量的影响,接下来采用方差分析的方法对其影响因素进行显著性检验。 对年份、地区和类别三个因素作方差分析,设年份、地区和类别三个因素分别为A,B,C。因素A年份有10个水平,i=1,2,…10,因素B有18个水平,j=1,2,…,18,因素C有5个水平,l=1,2,…,5。接下来对这三个因素两两进行检验如下: 2.4.1 年份和地区两因素对产量的方差分析 对于年份及地区两个因素对产量得影响,检验两个因素及它们的交互作用是否显著的假设为: H0A:αi=0,i=1,2,…10H1A:至少有一个i,使αi≠0 H0B:βj=0,j=1,2,…,18H1B:至少有一个j,使Bj≠0 2.4 HPV16/18阳性患者的阴道微生态状况 256例HPV阳性患者中,HPV16阳性80例,占31.3%;HPV18阳性27例,占10.5%;其他HPV亚型阳性149例,占58.2%。HPV16/18阳性患者中,BV发生率45.8%,高于其他HPV亚型阳性患者的发生率(32.2%),差异有统计学意义(P<0.05);而两组清洁度Ⅲ~Ⅳ度、pH≥4.5、TV、VVC发生率比较,差异无统计学意义(P>0.05)。多因素分析结果显示HPV16/18阳性与BV有明显相关性(OR=1.886,95%CI:1.113~3.196,P<0.05),见表2。 H0A×B:δij=0,i=1,2,…,10,j=1,2…,18H1A×B:至少存在一对i、j,使δij≠0 对于上述假设用SPSS做方差分析得下表5: 表5 主体间效应的检验因变量:增长率(%) 源III 型平方和df均方FSig.校正模型80609.800a161500.6821.3540.006截距9.86619.8660.0270.870年份3679.7558459.9691.2440.271地区12522.59817736.6231.9920.010年份 ∗ 地区64157.104136471.7431.2760.029误差229277.097620369.802总计309887.588782校正的总计309886.897781 显著性水平为α=0.05,查表可得F0.95(8,120)=2.97,F0.95(8,+∞)=2.93,故可得2.93 2.4.2 年份和类别两因素对产量的方差分析 对于年份和类别对产量的影响,检验两个因素及他们的交互作用是否显著的假设为: H0A:αi=,i=1,2,…,10H1A:至少有一个i,使αi≠0 H0A×C:ξil=0,i=1,2,…,10,l=1,2,…,5H1A×C:至少存在一对i,l,使ξil≠0 用SPSS做方差分析,得到表6: 表6 年份和类别间效应的检验因变量:增长率(%) 显著性水平为α=0.05,用表中的p值判断得,pA>0.05,pC<0.05,pA×C<0.05,可以拒绝H0C和H0A×C,即可认为不同类别的产值有显著的差异,年份和类别的交互作用对产量有显著性影响,年份对产量没有显著的影响。 2.4.3 地区和类别对产量的方差分析 对于地区、类别对产量的影响,检验两个因素及他们的交互作用是否显著的假设为: H0B:βj=0,j=1,2,……,18H1B:至少有一个j,使βj≠0 H0C:γ1=0,i=1,2,……,5H1C:至少有一个l,使γl≠0 H0B×C:ηjl=,j=1,2,…,18,l=1,2,……,5H1B×C:至少存在一对i,j,使δij≠0 用SPSS对其作方差分析,如表7: 表7 地区和类别间效应的检验因变量:增长率(%) 显著性水平为α=0.05,同样由p值得方法判断,可得pB<0.05,pC<0.05。所以可以拒绝H0B、H0C,即可认为不同地区,不同类别的产量有显著性差异。 由上述方差分析得到了类别和地区对产量增长率有显著性影响。依据分析的结果,并根据实际情况,可以调节河南省各地市渔业的发展情况,促进整个省渔业发展的最大化,更好的为人类提供观赏鱼,更好的为人类提供渔源食品。2 河南省2008年—2017年渔业生产的数据分析结果
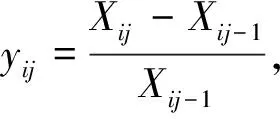
2.1 数据假设
2.2 数据预分析
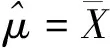
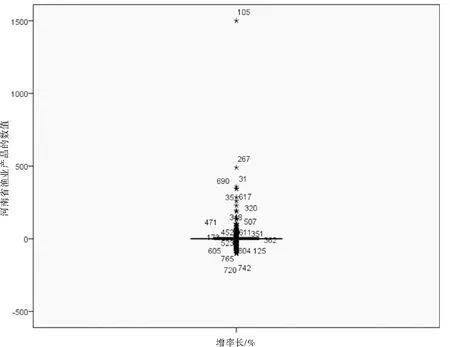
2.3 描述性统计分析
2.4 方差分析
3 总结
