基于排队论智能RGV的动态调度策略的研究

黎永壹，韩开旭

(1.北部湾大学，广西 钦州 535011；2.钦州市大数据资源利用重点实验室,广西 钦州 535011)

0 引 言

轨道自动导引车(Rail Guide Vehicle，RGV)因其具有速度快、成本低等特点，广泛用于自动化物流系统等领域。图1是一个智能加工系统的示意图，由8台计算机数控机床(Computer Number Controller，CNC)、1辆轨道式自动引导车(Rail Guide Vehicle，RGV)、1条RGV直线轨道、1条上料传送带、1条下料传送带等附属设备组成。RGV是一种无人驾驶、能在固定轨道上自由运行的智能车。它根据指令能自动控制移动方向和距离，并自带一个机械手臂、两只机械手爪和物料清洗槽，能够完成上下料及清洗物料等作业任务。两边排列的是CNC，每台CNC前方各安装有一段物料传送带。右侧为上料传送带，负责为CNC输送生料(未加工的物料)；左边为下料传送带，负责将成料(加工并清洗完成的物料)送出系统。

图1 智能加工系统示意图

目前，国内外学者对RGV调度路径的研究主要基于仓储系统。在国外，Lee et al.[1]研究了在基于FCFS的RGV调度策略下，自动化立体仓库中不同数量RGV的系统作业效率；Dotoli et al.[2]运用着色赋时Petri网研究了不同调度策略下自动化立体仓库的作业效率；Sáez et al.[3]通过提前预测将要产生的任务来有效完成多个RGV调度任务，即先采用模糊分类算法，根据历史数据求出将要产生任务的概率，再使用遗传算法找到合理的RGV调度路径。在国内，杨少华等[4-5]以环形轨道中多个RGV的调度策略为研究对象，利用排队论的思想构建了在不同系统状态下配置RGV数量的模型。吴长庆等[6-8]以自动小车存取系统中的控制问题为研究对象，利用双重着色赋时Petri网构建了多个RGV系统的实时模型，并采用RGV最短路径调度策略确定了系统工作效率。张桂琴等[9-10]介绍了一种避免碰撞的2-RGV直线调度策略。

本文根据RGV动态调度的工作特点，提出一种基于排队论的RGV动态调度的解决方案，结合伯努利概率解决CNC随机性故障RGV动态调度问题。

1 RGV智能加工系统工作原理及解决的问题

RGV工作过程一般有三种情况，第一，一道工序，无故障；第二，两道工序，无故障；第三，一道工序，有故障，CNC在加工过程中可能发生故障(据统计：故障的发生概率约为1%)的情况，每次故障排除(人工处理，未完成的物料报废)时间介于10～20 min之间，故障排除后即刻加入作业序列。系统作业参数的3组数据如表1所示。

表1 智能加工系统作业参数的3组数据表(时间单位：s)

注：每班次连续作业8 h。

首先，对一般问题进行研究，给出RGV动态调度模型和相应的求解算法；其次，利用表1中系统作业参数的3组数据分别检验模型的实用性和算法的有效性，给出RGV的调度策略和系统的作业效率，并记录具体的结果。

2 问题分析

由问题分析可知， RGV是一种直线轨道式工作系统，RGV可在轨道上左右移动进行上下料作业，因此整个问题可看作一个排队论问题。所以整个问题的核心是如何调度RGV，使其在一个满足任务动态变化的情况下，效率更高，这个效率可用花费的总时间来表示。

针对在第一种情况，我们要讨论只有一道工序时如何使RGV遍历完所有CNC，即完成一次往返所用时间最短或作业效率最高(所有CNC等待时间最短)，在排队论思想下，研究RGV所有运行路线的排列组合中的最优线路使得每台CNC的等待时间最少，根据产生的时间规律运用程序计算相应的数学模型既可得到所需。

针对第二种情况，由于涉及两道工序，且两道工序需分别在不同CNC完成，也是研究RGV所有运行路线的排列组合中的最优线路使得每台CNC的等待时间最少，根据产生的时间规律运用程序计算相应的数学模型既可得到所需。

针对第三种情况，分为一道工序，有故障和两道工序，有故障两种类型，由于存在发生故障概率，可考虑利用概率模型计算有k个故障同时概率，并计算CNC排除故障所消耗的时间，求出因故障导致增加时间。并将所得数据带入前两种情况的优化模型得到最终的模型。

3 模型假设

(1)RGV接受和发送指令信号时间很短，可忽略不计；

(2)上下料传送带一直处于工作状态且速度很快，对调度优化问题不产生影响；

(3)RGV调度系统无故障，可实时知道材料加工情况和小车实时位置；

(4)每一边CNC之间的距离两两相等；

(5)两道工序的物料在机械手抓上转换方向的时间忽略不计；

(6)两道工序的物料加工过程处于不中断；

(7)有两道工序的物料加工，在第一道工序结束时不进行清洗作业。

4 符号说明

表2 符号说明

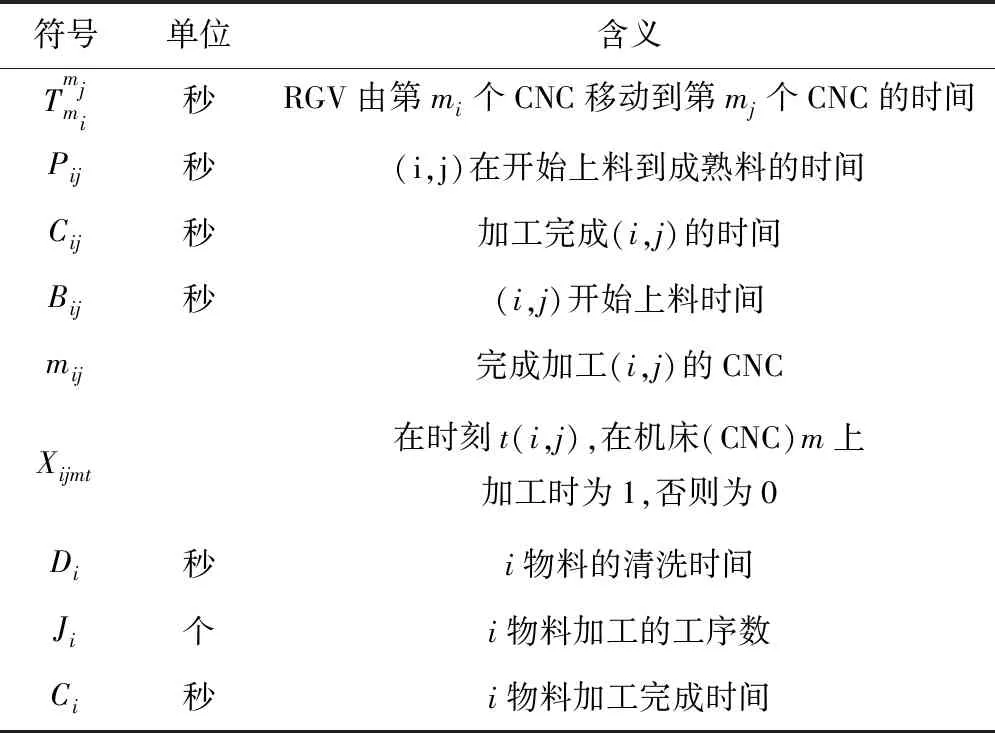
续表2

5 模型的建立与求解

5.1 第一种情况模型的建立与求解

5.1.1问题分析

由于每台CNC安装的是相同的刀具，且只能完成一道工序，又物料的加工只有一道工序，因此物料可以在任意一台CNC上加工完成。RGV上下料的时间小于CNC处理的时间，因此可循环进行。当RGV的一个往返所用时间最短或系统作业效率最高时，在规定的时间内，即可使成料总数量最多，提高智能系统的加工效率。

5.1.2模型的建立与求解

为了找出RGV所有一个往返运行路线的排列组合中的最优路径，最简单有效的方法是排队论，通过计算每个排列组合所花费的时间，筛选出运行路线所用时间最短或者系统作业效率最高的最优组合，使得成料总数量最多[11]。

设用：

(1)

其中，Cim是指物料i在m编号CNC上下料的时间。

由于一台CNC只能加工一个物料，则：

(2)

对物料的工序加工时间约束：

Pij=Cij-Bij(i=1,2,…,N;j=1,2,…,Ji)

(3)

考虑物料的运输时间及按照特定工序步骤进行加工：

(4)

同时保证CNC加工时间不中断：

(5)

物料完成时间和加工时间的关系：

Ci=CiJi(i=1,2,…,N)

(6)

T：RGV走一圈这一个往返过程所花费时间。

(7)

其中i=1,2,…,N;j=1,2,…,Ji

Tf：CNC加工物料时间与RGV走一圈这一个往返过程所花费时间的两者时间之和。

Tf=T+Pij

(8)

其中i=1,2,…,N;j=1,2,…,Ji

综上所述可得动态规划模型为：

(9)

Tf=T+Pij

(9-1)

(10)

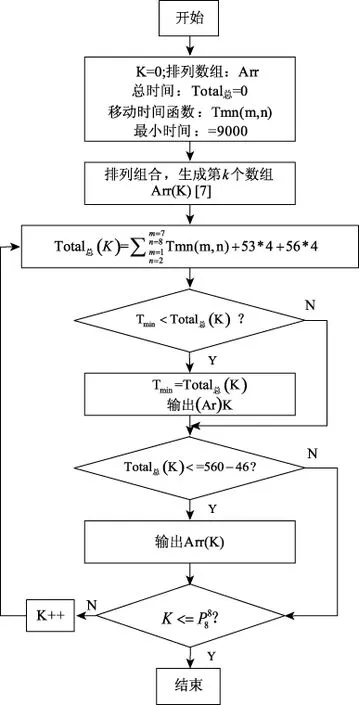
图2 完成一道工序动态调度求最优组合求解流程图

根据图1流程图，算法步骤如下：

首先，初始化变量、函数，主要的变量和函数有：排列组合序号K，两个CNC之间的移动时间函数Tmn(m,n)，最小时间Tmin。

其次，根据队列论的要素，求出排列组合，以数组的形式保存，第K个排列组合记为Arr(K)[7]，并计算该排列组合的总时间。

然后，经过对题目的分析，根据队列论确定最优组合的条件为完成物料加工总时间最短或系统作业效率最高，并输出最优组合，有如下两种具体情况：其一、计算每个排列组合的总时间之后与最小时间对比，输出总时间最小的组合；其二、为了提高系统作业效率，应该尽量减小CNC的等待时间，因此，若RGV能在560 s内回到起始CNC，则输出该最优组合。

最后，按照以上规则完成所有的排列组合，当K达到所有组合总数时结束。

程序运行结果如下表3所示，根据动态规划模型，设计动态调度求解算法，通过C#语言编程，计算出最短时间，并输出最短时间496 s及RGV在560 s内回到初始CNC的96个最优组合。

5.2 第二种情况 模型的建立与求解

5.2.1问题分析

由于物料的加工工序为两道，RGV完成工作时间也随之增加，同样利用排队论，解决两道工作的问题，也就是要建立完成两道RGV一次往返所用时间最短的数学模型，计算每个排列组合所花费的时间，找出运行两道所用时间最短或系统作业效率最高的最优组合，使得两道工作成料数量最多。

表3 一道工序无故障最优组合表

5.2.2模型的建立与求解

CNC加工物料时间与RGV走一圈这一个往返过程所花费时间的两者时间之和为：

Tf=T+Pij1+Pij2

(11)

其中Pij1是物料的第一道工序从开始上料到成熟料的时间;Pij2是物料的第二道工序从开始上料到成熟料的时间。

RGV走一圈这一个往返过程所花费时间为：

(12)

其中Dij2为第二道工序结束的清洗作业时间。

考虑到一台CNC只能加工一个物料，则：

(13)

考虑物料的运输时间及按照特定工序步骤进行加工：

(14)

对物料的工序加工时间约束：

Pij=Cij-Bij(i=1,2,…,N;j=1,2,…,Ji)

(15)

同时保证CNC加工时间不中断：

(16)

综合上述可得动态规划模型为：

Tf=T+Pij1+Pij2

(17)

(18)

(19)

然后利用C#语言编程对所有RGV运行线路的排列组合进行分析，可得到RGV运行线路为最优组合，结果如表4、表5所示。

表4 完成两道工序无故障的第1组最优组合表

表5 完成两道工序无故障的第2组最优组合表

5.3 第三种情况 模型的建立与求解

5.3.1问题分析

由于出现故障，因此导致所用时间增多，因为这是一个组合概率问题，所以，可用伯努利概率模型求解出同时有K台发生故障的概率，再计算CNC发生故障到被排除所耗费的时间，最终得到总的排除故障所需时间，即为所求的增加的时间，再把数据放入前两个最优模型中，建立最优的数学模型。

5.3.2模型的建立与求解

由于产生故障，结合第一和第二两种情况

运用伯努利概率模型[12-13]，假设有n台CNC，每台CNC故障的发生概率均约为1%,则恰好有y台故障发生的概率P为：

(20)[14]

一个CNC发生故障到被排除所耗费的时间为：

(21)

故障处理的总时间为：

(22)

当工序为一道时：

(23)

Tf=T+Pij+Td总

(24)

(25)

当工序为两道时：

Tf=T+Pij1+Pij2+Td总

(26)

(27)

(28)

由公式(20)、(21)计算得到每一种故障情况的影响时间，利用Excel得到结果，具体如表6、表7所示。

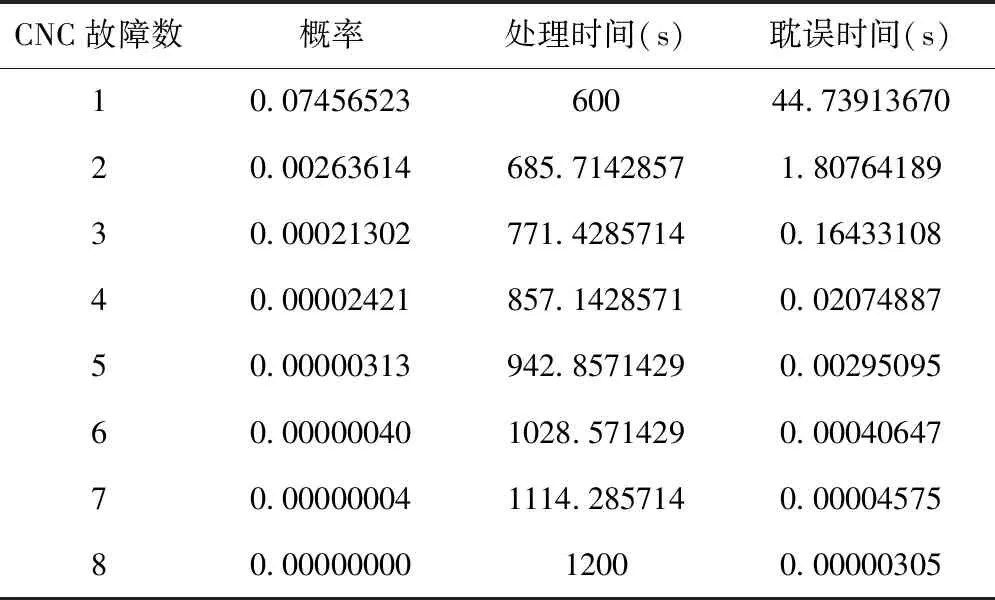
表6 CNC发生故障影响时间表

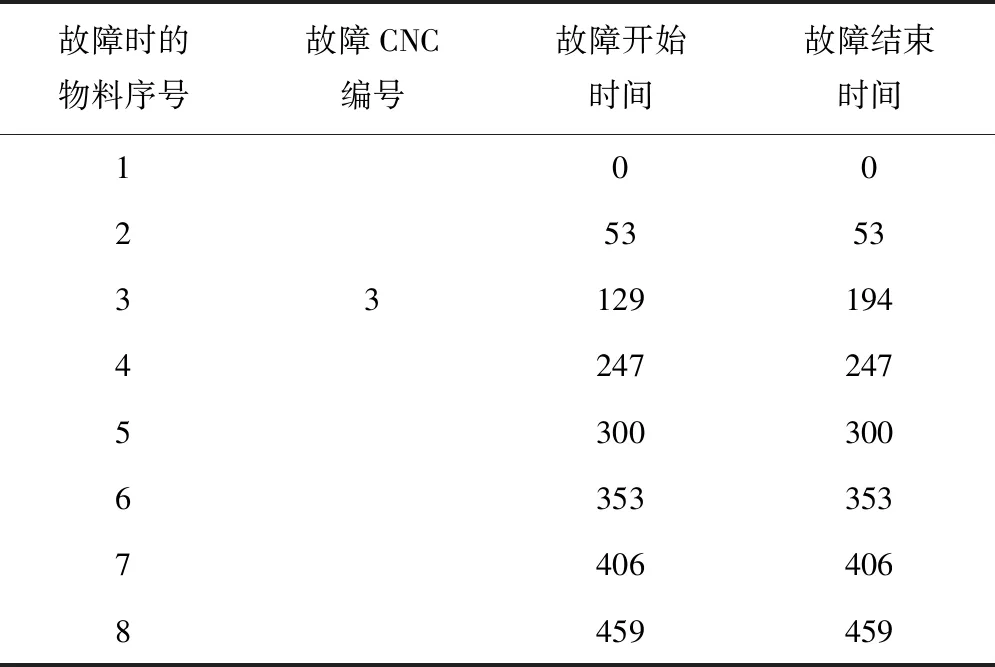
表7 第1组数据随机抽取1台CNC故障数据表

6 结 语

对于本题的模型设计思路，根据题目所知RGV上下料的时间小于CNC处理的时间，因此可循环进行。因此将整个问题看作一个排队论问题，对所有RGV的一次往返运行进行排列组合，通过对这个排列组合计算目标并与最优条件比较判断确定最优路线[15]。

针对第一种情况，运用排队论，找出RGV所有一个往返运行路线的排列组合中的最优路径，建立了以RGV运行时间最短或系统作业效率最高为目标的优化模型，通过计算每个排列组合所花费的时间，筛选出运行路线所用时间最短或者系统作业效率最高的最优组合，根据动态规划模型，设计动态调度求解算法，通过C#语言编程，计算出最短时间，并输出最短时间496 s及RGV在560 s内回到初始CNC的最优组合，使得达到成料数量最多[16]。

针对第二种情况，由于物料的加工工序为两道，CNC的加工时间以及RGV运行一个往返的时间相应增加，因此，根据排队论，在RGV所有线路的排列组合中，建立了以RGV走一圈即完成一次往返所用时间最短或系统工作效率最高为目标的数学模型，通过计算每个排列组合所花费的时间，筛选出运行路线所用时间最短或者系统作业效率最高的最优项，使得达到成料数量最多[17]。

针对第三种情况，运用伯努利概率模型计算出恰好有y台CNC同时发生故障的概率，再计算CNC发生故障到被排除所耗费的时间，最终得到总的排除故障所需时间，再结合前述两种情况未发生故障时最优组合，建立最优的数学模型。

利用排队论解决智能RGV动态调度问题，主要解决的是RGV三中情况的最优组合求解问题，相对于采用模糊分类算法、遗传算法及构建网络等其他方法，更有针对性和有效性，具有如下优点：(1)当n(CNC个数)不是很大时，文中提出的算法复杂度相对较小。(2)运用C#和Excel对RGV的所有一次往返的运行线路的排列组合进行数据处理，具有快捷准确的特点，使得数据处理变得简单。(3)运用排队论对RGV的运行线路进行排列组合，使得对所有运行线路清晰明了。从整体上提供加工系统的工作效率，使在同等的时间内达到成料数理最多[18]。