基于弹簧的绳驱动4-SPS/U刚柔并联式躯干关节机构设计与运动学建模
2019-12-23潘以涛陈原王立栋路浩
潘以涛, 陈原, 王立栋, 路浩
(山东大学(威海) 机电与信息工程学院, 山东 威海 264209)
0 引言
战场、地震及矿井灾害等环境既有常规障碍,如斜坡、台阶、壕沟、坑洼、石柱等,也有大尺度岩石、大跨度壕沟、超低矮桥梁、极狭窄洞穴、深浅不定水域等更复杂的地形环境。在上述这些环境中进行一些作业任务的多运动模式移动机器人必须具备运动模式多、灵活性好以及越障能力强等优点[1-3]。
目前,多运动模式移动机器人主要由轮式、履带式和腿式等移动单元组合而成的。李志海[4]设计了一种轮- 足混合式壁面移动机器人,该机器人结合了轮式和足式移动机构的优点,通过轮- 足5杆切换机构实现了轮式移动和足式移动之间的转换。该轮- 足混合式结构使机器人吸附稳定、移动速度快和转弯灵活,但是它不能完成机器人躯干的弯曲姿态调整,使轮- 足无法正常地接触高低起伏的地面,也就使得该类机器人只适合攀爬平面。中国科学技术大学研发的HyTRo-I轮- 腿复合式移动机器人,它通过腿部机构的折叠收缩来实现轮子移动、抬升和脱离等动作[5];但是,该腿部机构在转换腿式移动时,易将轮子锁死,只适合起伏小的平面移动。中国科学院沈阳自动化研究所研制了轮- 履带复合式移动机器人,它通过履带摆臂结构来实现轮式移动和履带式移动的复合运动[6];但是,该机器人的结构尺寸和质量较大,也缺少躯干的柔性弯曲姿态调整功能,无法实现崎岖狭小空洞内移动。Phipps等[7]提出了一种可变形6足移动机器人,当6足移动机构收缩时可实现球形滚动,而6足张开时就能通过腿足进行移动;但是,该移动机器人不具有躯干关节机构,无法进行柔性身躯调整,也就很难实现攀爬起伏不定的大斜度坡。
现有的多运动模式移动机器人仅考虑移动单元之间的组合,而忽略了机器人躯干关节机构的作用。躯干关节机构的柔性重心调整,再配合移动机构的灵活运动,可使移动机器人实现平稳且多样的运动姿态调整功能。因此,躯干关节机构对提高多运动模式移动机器人全身协调运动灵活性能发挥不可替代的作用。国内外有一些研究机构对躯干关节机构进行了设计,如日本早稻田大学研制的 WABIAN-2R机器人[8-9],其躯干是采用髋部和腰部的串联驱动方式。其具有更多自由度的躯干设计可以使得仿人机器人能实现更类似于人的步态运动,比如通过骨盆的转动使得机器人在跨步向前时,腿部可以完全伸展,还能实现向外撇腿,在软垫层上原地踏步等复杂动作;但其腰部机构也存在着结构复杂、质量过重等问题。德国人工智能研究中心和不来梅大学联合研制的 i Struct类猿太空探索机器人[10],其躯干采用 6 自由度的并联机构,使得机器人具有很好的承载能力,提高了机器人的刚性,减少了误差累积,提高了运动精度;然而,并联躯干机构的运动范围小,限制了机器人进行灵活的运动。欧洲创新大学协会开发了 i Cub机器人[11],它的俯仰和偏转运动是由钢丝绳驱动的差分机构实现;采用这种柔索驱动方式,使仿人机器人腰部具有柔性,但是这种驱动方式也存在着驱动力较小的问题,难以在较大负载的应用场合下保持足够的刚度。
多运动模式移动机器人的躯干关节机构不仅具备柔性姿态调整来灵活实现行走、水中推进、攀爬以及滚动等多种运动模式,而且还须具备一定的刚度和抗干扰承载能力来精确地保持穿梭、行走和攀爬等多种运动姿态。少自由度刚性并联机构可以提供不同方向的导向姿态变化,但是它存在位姿摆动空间小、奇异位姿多和柔性差等缺点[12-13]。纯绳驱动并联机构可以通过增加绳索条数来实现机器人末端的高精度位姿定位[14-15],也能通过减少铰链转角的限制来增大末端位姿空间,但是,纯绳驱动并联机构存在刚度不足缺点。如果在绳驱动并联机构中添加刚性约束支链,那么该机构不仅能够灵活地实现不同方向空间姿态的变化[16-20],而且也可以使机构具备一定的刚度和承载能力。本文结合绳驱动和刚性并联机构二者的优点,采用过约束并联机构的构造方法,创新设计了一种2自由度绳驱动4-SPS/U刚柔并联式躯干关节机构。
首先,本文采用螺旋理论对绳驱动刚柔并联式躯干关节机构进行了机构自由度的计算;其次,结合封闭矢量方法和特征结构配置解耦法构建了该机构的运动学逆解模型;再次,建立了该机构的速度和加速度数学模型,分析了绳驱动刚柔并联式躯干关节机构的奇异性;最后,给出了运动学算例仿真,验证了运动学模型的正确性。
1 绳驱动4-SPS/U刚柔并联式躯干关节机构
1.1 躯干关节机构的创新设计
如图1(a)所示,绳驱动4-SPS/U刚柔并联式躯干关节机构是由动平台、静平台以及连接动平台和静平台的约束支链和驱动支链所组成。如图1(a)中整体机构图所示,驱动支链包括4条结构相同的绳驱动SPS刚柔支链。如图1(a)中上、下移动机构图所示,先将上、下球铰分别装配在动、静平台的球铰座处,上球铰设置弹簧座,下球铰设置弹簧座。如图1(a)中柔刚组合机构图所示,将弹簧嵌入在上、下球铰的弹簧座之间,用来提高刚性。如图1(a)中下移动机构图所示:静平台上每个球铰座底部都设穿线孔,下球铰中心部也设有穿线孔;再把绳索一端穿过静平台的球铰座穿线孔,穿过上下球铰弹簧座之间弹簧,最后固定在上球铰的弹簧座上,另一端固定在静平台底部的绞线轮中固线架上,从而组合成基于弹簧的绳驱动SPS刚柔支链。如图1(a)中约束支链机构图所示,约束支链是将相同方向的虎克铰轴端通过滑动轴承装配在动、静平台支架的两侧之间,形成一条中间被动约束支链U. 通过静平台底部的相应电机带动绞线轮改变每条绳驱动支链中绳索长度的变化,并在弹簧弹性力作用下,可以实现绳驱动支链的伸缩运动,从而将电机输出的扭矩转化为直线推力和拉力[21-25]。
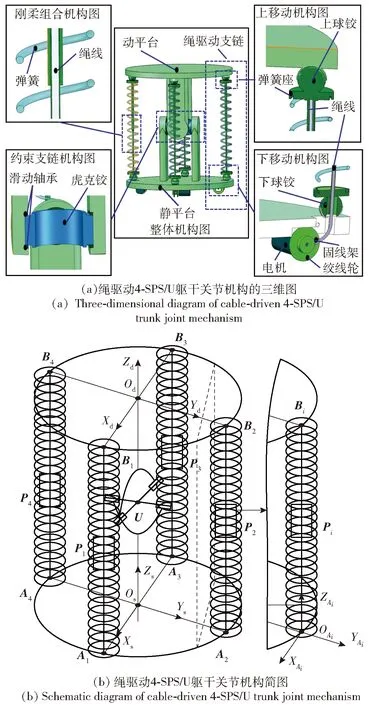
图1 绳驱动4-SPS/U刚柔并联式躯干关节机构Fig.1 Cable-driven 4-SPS/U rigid-flexible parallel trunk joint mechanism
如图1(b)所示,将与静平台相连的球副设为第1运动副(点A1,A2,A3,A4),移动副设为第2运动副(P1,P2,P3,P4),与动平台相连的球副设为第3运动副(点B1,B2,B3,B4)。OsXsYsZs是位于静平台圆心处的静坐标系,OdXdYdZd是位于动平台圆心处的动坐标系。Os点位于半径为r的静平台圆心处,Xs轴沿着A3A1,Ys轴沿着A4A2,Zs轴符合右手定则;Od点位于半径为r的动平台的圆心处,Xd轴沿着B3B1,Yd轴沿着B4B2,Zd轴符合右手定则。同时为了方便自由度计算,在绳驱动支链AiBi上建立支链坐标系OAiXAiYAiZAi(i表示第i条驱动支链,即i=1,2,3,4),OAi位于静平台球铰处,XAi轴平行于Xs轴,YAi轴平行于Ys轴,ZAi符合右手定则。Pi表示第i条SPS支链移动副轴线的单位矢量。
如图2所示,基于上述躯干关节机构,该多运动模式6足移动机器人由头部结构、腿部机构、躯干机构及螺旋桨推进结构等组成,其躯干机构是由4个如图1所示的绳驱动4-SPS/U刚柔并联式躯干关节机构串联构成。通过躯干机构中每个躯干关节机构的姿态变化,可使该6足移动机器人实现和提高多种运动模式的能力。如图2行走姿态图所示,该6足移动机器人能实现前、中、后腿之间的变方向弯曲轨迹爬行;如图2水中推进姿态图所示,将6条腿收缩,再通过躯干关节机构姿态多样性调整,机器人就能实现头部结构与尾部的螺旋桨推进结构之间的矢量推进;如图2攀爬姿态图所示,在爬越障碍物时,如楼梯、壕沟等,通过躯干关节机构来调整躯干不同部位之间的弯曲变化,可以调整机器人攀爬过程中前、中、后腿之间的重心位置,从而提高攀爬能力;如图2滚动姿态图所示,在平滑和缓坡处,将6条腿收缩,再通过躯干关节机构调整躯干不同部位之间的弯曲扭动,可以实现像蛇一样的爬行姿态,也可以进行整体滚动运动。
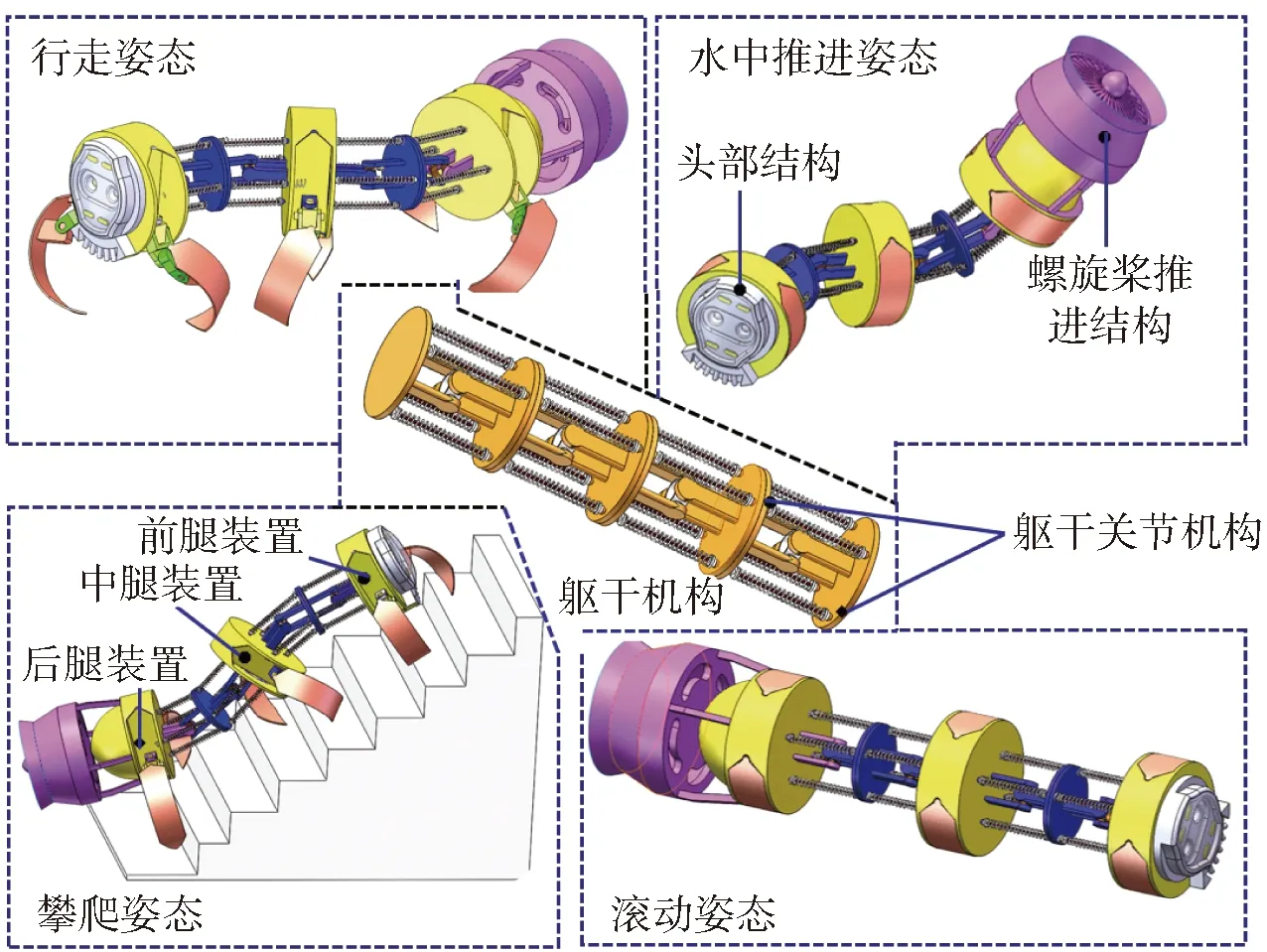
图2 多运动模式6足移动机器人结构组成及其运动姿态Fig.2 Structure and moving postures of multi-mode mobile hexapod robot
如图3所示,其躯干机构的驱动方式可以设计为欠驱动和冗余驱动这两种方式。如图3(a)所示为欠驱动方式,4个驱动控制4条绳索实现躯干机构的2自由度弯曲运动。如图 3(b)所示为冗余驱动方式,每个躯干关节机构都可以各自通过4个驱动控制4条绳索来实现2自由度弯曲摆动,冗余驱动可使机器人实现多关节不同角度弯曲运动。与欠驱动方式相比,冗余驱动方式能充分发挥每个躯干关节机构的独立运动灵活性[26-27],可调整前、中、后腿之间的重心位置,适合本文提出的多运动模式移动机器人。
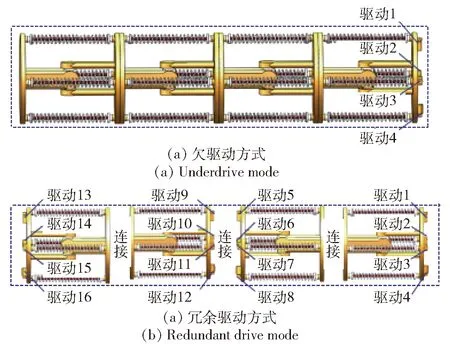
图3 躯干机构的驱动方式Fig.3 Driving mode of trunk mechanism
1.2 绳驱动4-SPS/U刚柔并联式躯干关节机构的自由度计算
采用修正Kutzbach-Grübler公式[28]对该机构自由度进行计算:
(1)
式中:M表示机构自由度数;d表示机构的阶数,它依赖于公共约束λ,d=6-λ;n表示包括机架的构件数目;g表示运动副的数目;fi表示第i个运动副的自由度;υ表示为多环并联机构的冗余约束,它等于在去除公共约束的因素后独立冗余约束的数目,υ=y-k,y表示多环并联机构所有支链的反螺旋去除公共约束后反螺旋数目,k表示多环并联机构所有支链的反螺旋去除公共约束后反螺旋系的最大无关组;ζ表示机构中存在的局部自由度。
图2中的4条绳驱动支链在支链坐标系OAiXAiYAiZAi中的运动螺旋系为
(2)
式中:Mi表示第i条驱动支链上第2运动副轴线的方向余旋;Pi表示第i条驱动支链上第3运动副相对于坐标系OAιXAiYAiZAi的位置。
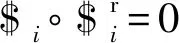
在参考坐标系OdXdYdZd下,中间约束支链OsOd的运动螺旋系$51、$52分别为
(3)

(4)
由(4)式可知,该机构螺旋系限制了动平台的Yd轴、Xd轴、Zd轴的移动以及Zd轴的转动,则有y=4,k=4. 再依据公式υ=y-k可得:υ=4-4=0. 通过观察整个绳驱动4-SPS/U刚柔并联式躯干关节机构的运动支链布置情况,此4条结构相同的绳驱动SPS支链均存在局部自由度,即ζ=4. 因此,由(1)式可以计算出该机构自由度为
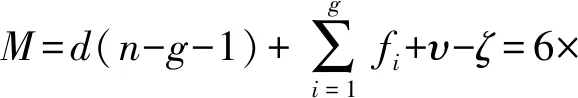
2 绳驱动4-SPS/U刚柔并联式躯干关节机构的运动建模
2.1 位置逆解建模
如图4所示,分别在静平台中心建立坐标系OsXsYsZs,在虎克铰中心建立坐标系OHXHYHZH以及在动平台中心建立坐标系OdXdYdZd,4条驱动SPS支链的两端球铰点分别位于静平台上的点A1、A2、A3、A4,以及动平台上点B1、B2、B3、B4,并且均匀对称分布。静平台和动平台球铰点到圆心的距离均为r,中间约束支链U位于静平台和动平台之间,且虎克铰中心到上下平台中心点距离均为l.Li表示第i条SPS支链移动副轴线的长度。
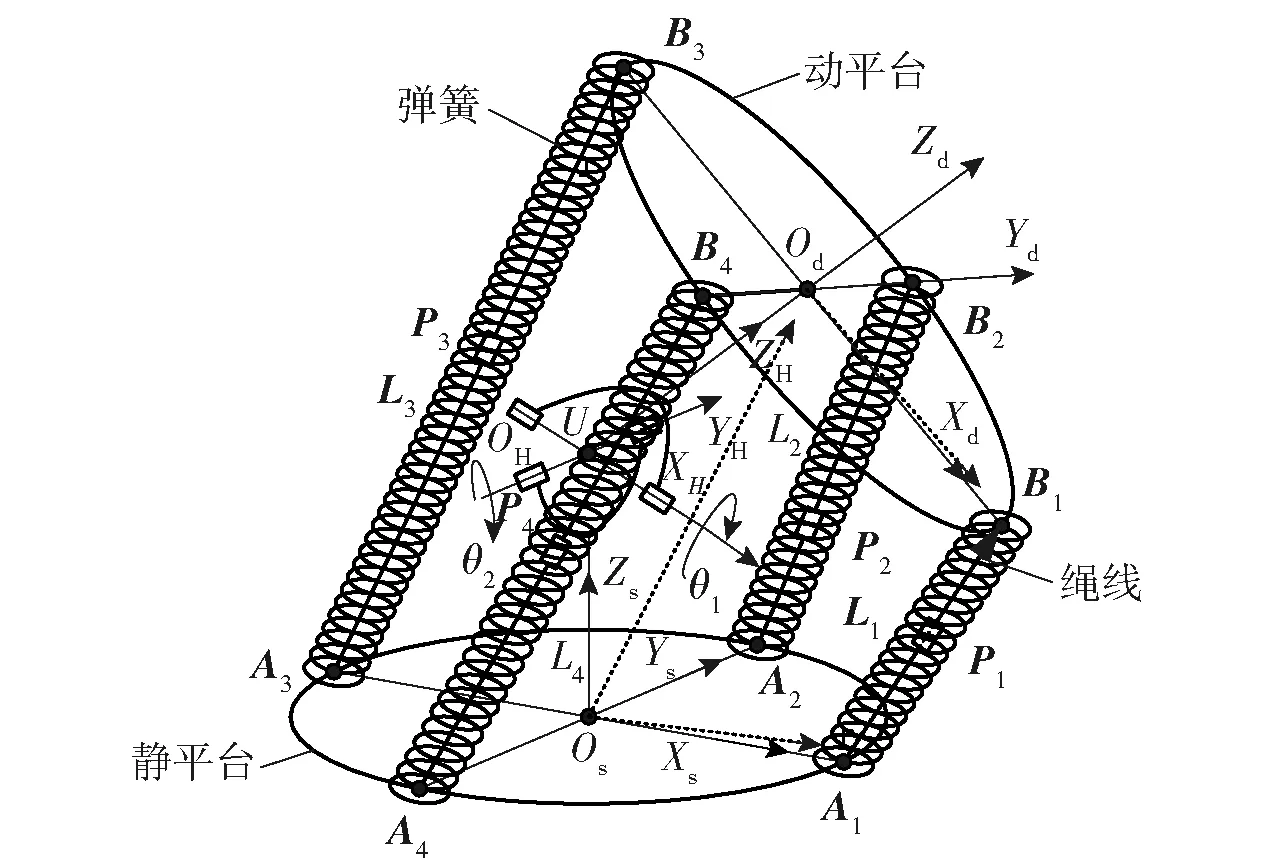
图4 绳驱动4-SPS/U刚柔并联式躯干关节机构简图Fig.4 Sketch of cable-driven 4-SPS/U rigid-flexible parallel trunk joint mechanism
如图4所示,虎克铰中心处的坐标系OHXHYHZH绕YH轴转动θ2,动坐标系OdXdYdZd绕XH轴转动θ1,则可以求得动坐标系OdXdYdZd相对于静坐系OsXsYsZs的齐次变换矩阵为

(5)
如图4所示,由黑色虚线箭头形成的A1OsOdB1矢量封闭法[29]可求得每条绳驱动支链长度AiBi的变化方程:
AiBi=OsOd+OdBi-OsAi,
(6)
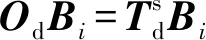
(7)
由(7)式可知,该机构中各条绳驱动支链长度AiBi均为独立显示方程,当给定动平台转动角度θ1和θ2时,可直接通过(7)式求得各条绳驱动支链长度Li. 因此,绳驱动4-SPS/U刚柔并联式躯干关节机构的位置逆解可写为
Li=‖AiBi‖,i=1,2,3,4.
(8)
2.2 速度和加速度建模

(9)
式中:Jij的第i行第j列元素是由(8)式中的AiBi对θj求导数得出;L是第i条绳驱动支链长度单位矩阵。假定Jm为该机构的正雅克比矩阵,Jm=L-1Jij.
4条绳驱动SPS支链的第1支链与第3支链,以及第2支链与第4支链之间存在耦合关系,所以已知相邻两条绳索驱动支链的速度,就可求解绳驱动4-SPS/U刚柔并联式躯干关节机构的速度正解方程为
(10)
(9)式两边同时对时间t求导,可求得绳驱动4-SPS/U刚柔并联式躯干关节机构的加速度逆解方程为
(11)
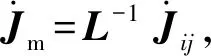
3 绳驱动4-SPS/U刚柔并联式躯干关节机构的奇异性分析
如图5所示,S19和S29分别表示中间约束支链中虎克铰链在动平台轴线上的单位矢量。
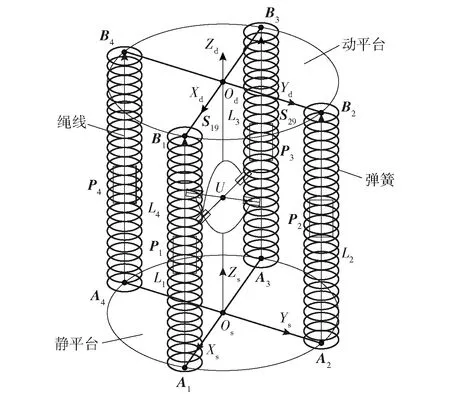
图5 躯干关节机构的奇异性分析原理图Fig.5 Singularity analysis of trunk joint mechanism
根据螺旋理论中瞬时运动的概念,设定Sj,i(j=1, 2, …,7;i=1,2,3,4)表示第i条绳驱动SPS支链中运动副的第j个方向的单位矢量。可得每条绳驱动SPS支链在动坐标系OdXdYdZd中的单位运动螺旋如下:
1) 静平台球铰链沿三轴的单位运动螺旋$s,z,i(z=1,2,3)为
(12)
2)绳驱动SPS支链移动副的单位运动螺旋$s,4,i为
(13)
3)动平台球铰链沿三轴的单位运动螺旋$d,z,i(z=5,7,8)为
(14)
由(12)式、(13)式和(14)式可得4条绳驱动SPS支链产生的瞬时运动螺旋$b为
(15)
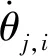
SPS支链中绳驱动移动副锁定,则由螺旋对偶性可求得该支链相对其他运动副的反螺旋为
(16)
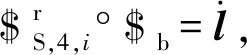
(17)
式中:每一行矢量元素代表该机构运动所需的驱动力螺旋。
中间约束支链的虎克铰沿两轴线在坐标系OdXdYdZd下的单位运动螺旋为
(18)
由互易积求得中间约束支链的4个反螺旋为
(19)
式中:n39=S29×S19;n49=S29×S19.
由(18)式可求得中间约束支链产生的瞬时运动螺旋$m为
(20)
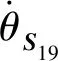
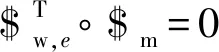
(21)
式中:第1行、第2行和第3行矢量代表该机构施加的单位约束力螺旋,第4行矢量代表该机构施加的单位约束力偶螺旋。
(17)式和(21)式合并成绳驱动4-SPS/U刚柔并联式躯干关节机构的雅克比矩阵J为
(22)
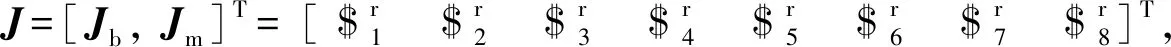
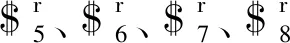
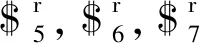
在动平台运动过程中,与绳驱动支链相关的Jb矩阵包含4个行矢量,它们的线性相关性分析如下:
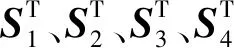
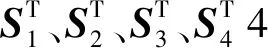
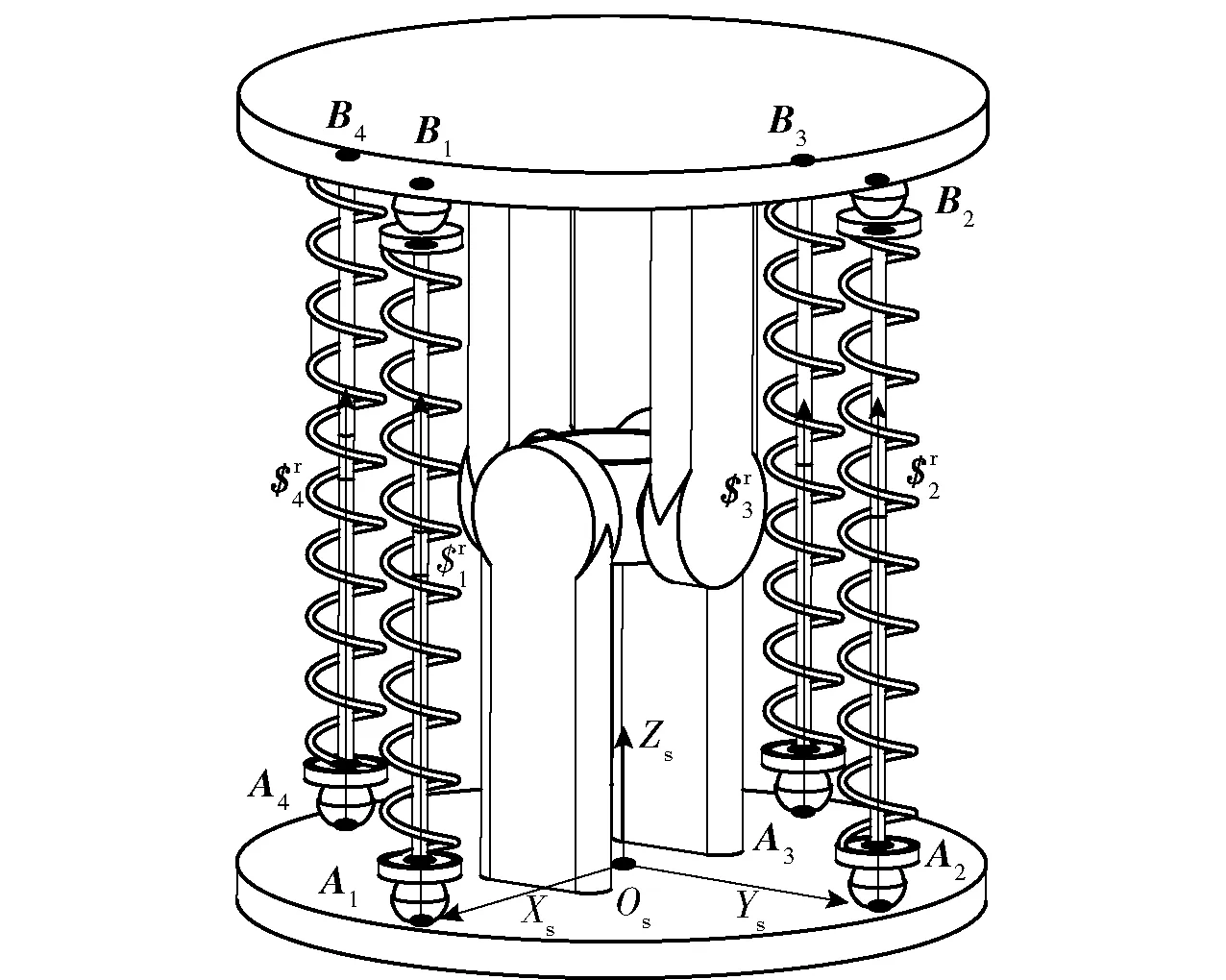
图6 4条平行SPS绳驱动支链Fig.6 Four SPS parallel cable-driven chains
综上所述,绳驱动4-SPS/U刚柔并联式躯干关节机构的雅克比矩阵J的秩可以表示为
rank(J)=rank(Jm)+rank(Jb)=5.
(23)
由(23)式可知,当rank(J)<6时,雅克比矩阵不满秩,机构存在奇异性。又因为当rank(J)=5时,4条绳驱动SPS支链是在初始时刻位置平行,所以该机构在运动过程中没有奇异性位置,具有良好的运动和力传递能力。
4 绳驱动4-SPS/U刚柔并联式躯干关节机构的工作空间分析
该机构动平台的广义位置坐标可表示为Φθ=[θ1,θ2]T,其中θ1、θ2为动坐标系OdXdYdZd相对于静坐表系OsXsYsZs的转角。如图7所示,绳驱动支链绳索li的单位向量分别为Pi,中间约束支链的杆件长度为l及单位向量表示为P5,动平台和静平台的姿态向量分别为P6、P7.
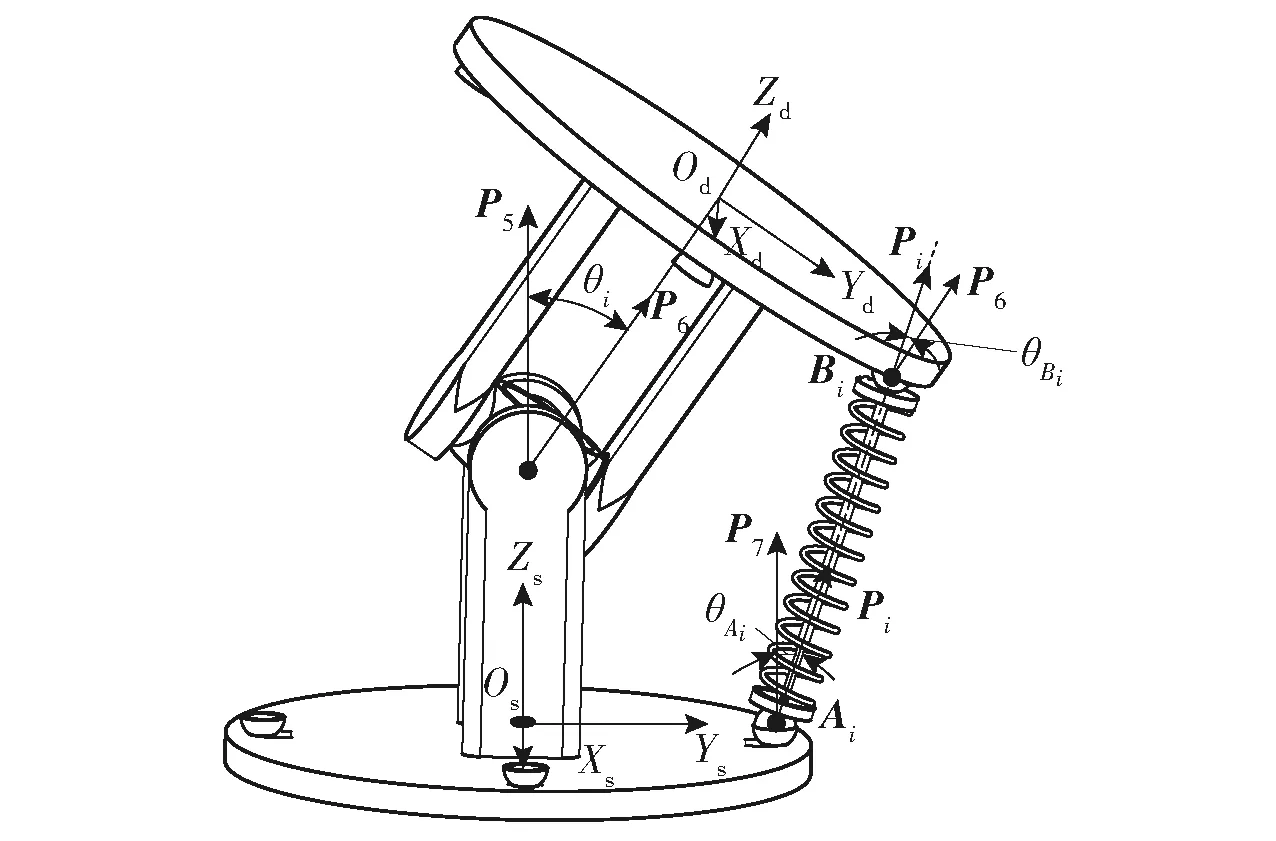
图7 绳驱动4-SPS/U躯干关节机构的转角约束Fig.7 Corner constraint of cable-driven 4-SPS/U rigid-flexible parallel trunk joint mechanism
弹簧收缩和刚性套筒的相对移动距离有极限位置,故绳驱动支链绳索长度的变化是有约束限制条件的。假设每条绳索的最小长度和最大长度分别为Limin和Limax,那么每条绳驱动支链在驱动过程中绳索长度Li的约束条件可以表示为:
Limin≤Li≤Limax.
(24)
与动平台相连的球铰θBi、与静平台相连的球铰θAi以及与动平台相连的万向铰θi的约束限制条件为
(25)
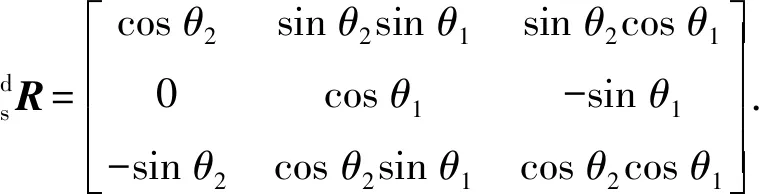
5 数值算例
5.1 工作空间的仿真计算
绳驱动4-SPS/U刚柔并联式躯干关机构的参数设置为:r=178.5 mm,l=200 mm,Limin=222.3 mm,Limax=515 mm,θBimax=90°,θAimax=90°,-45°≤θimax≤-45°. 通过数值搜索法,在MATLAB软件中以该机构绳驱动支链长度、中心约束支链U副转角及关节转角为限制条件进行其姿态工作空间仿真。可得如图8所示绳驱动4-SPS/U刚柔并联式躯干关节机构的三维工作空间。
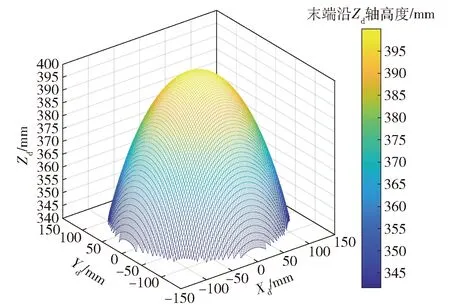
图8 绳驱动4-SPS/U刚柔并联式躯干关节机构的三维工作空间Fig.8 3D workspace of 4-SPS/U rigid-flexible parallel trunk joint mechanism
从图8三维工作区间可知,该机构工作空间呈局部球面状,Zd轴坐标值的变化范围为340~395 mm,投影到OdXdYd平面内是半径为150 mm的圆,三维空间内没有空洞,具有良好、较大的姿态运动性能。
5.2 运动学模型的仿真分析
定义角度输入轨迹为
由工作空间仿真中机构参数可得,采用MATLAB软件对(8)式进行仿真计算,可得到绳驱动4-SPS/U刚柔并联式躯干关节机构的4条绳驱动支链在Zd轴方向上的位移Li随时间t变化曲线,如图9所示。为了验证数值计算的正确性,将绳驱动4-SPS/U刚柔并联式躯干关节机构的三维机械制图软件SolidWorks 模型导入到仿真软件Adams中,并进行仿真分析,得到了如图10所示的4条绳驱动支链在Zd轴方向上的位移Li随时间t变化曲线。对比图9和图10可知,理论仿真曲线和Adams软件仿真结果几乎完全重合,从而证实了运动学建模的正确性。

图9 4条绳驱动支链的位移理论仿真曲线Fig.9 Theoretically simulated displacement curves of four cable-driven chains
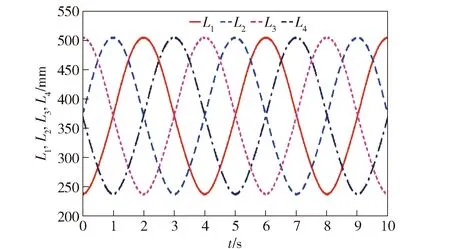
图10 4条绳驱动支链的位移Adams仿真曲线Fig.10 Simulated displacement curves of four cable-driven chains by Adams
通过采用MATLAB软件对(9)式和(11)式进行仿真计算,可得到绳驱动4-SPS/U刚柔并联式躯干关节机构的4条绳驱动支链在Zd轴方向上的速度vi和加速度ai随时间t变化曲线,如图11 、图12所示。为了验证数值计算的正确性,将其该机构的 SolidWorks 模型导入到Adams仿真软件中,并进行仿真分析,得到了如图13、图14所示的4条绳驱动支链在Zd轴方向上的速度vi和加速度ai随时间t变化曲线。对比图11和图13、图12和图14可知,理论仿真曲线和Adams软件仿真结果几乎完全重合,从而证实了运动学建模的正确性。
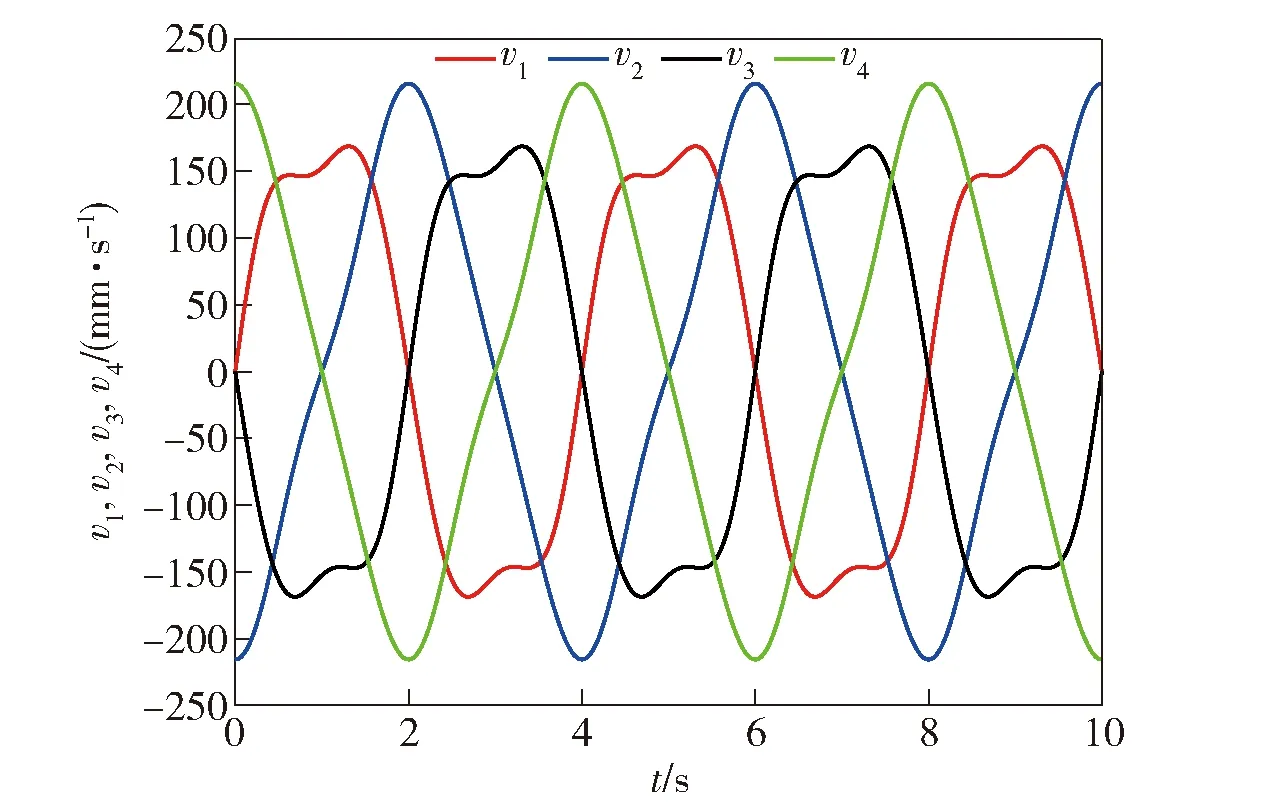
图11 4条绳驱动支链的速度理论仿真曲线Fig.11 Simulated velocity curves of four cable-driven chains
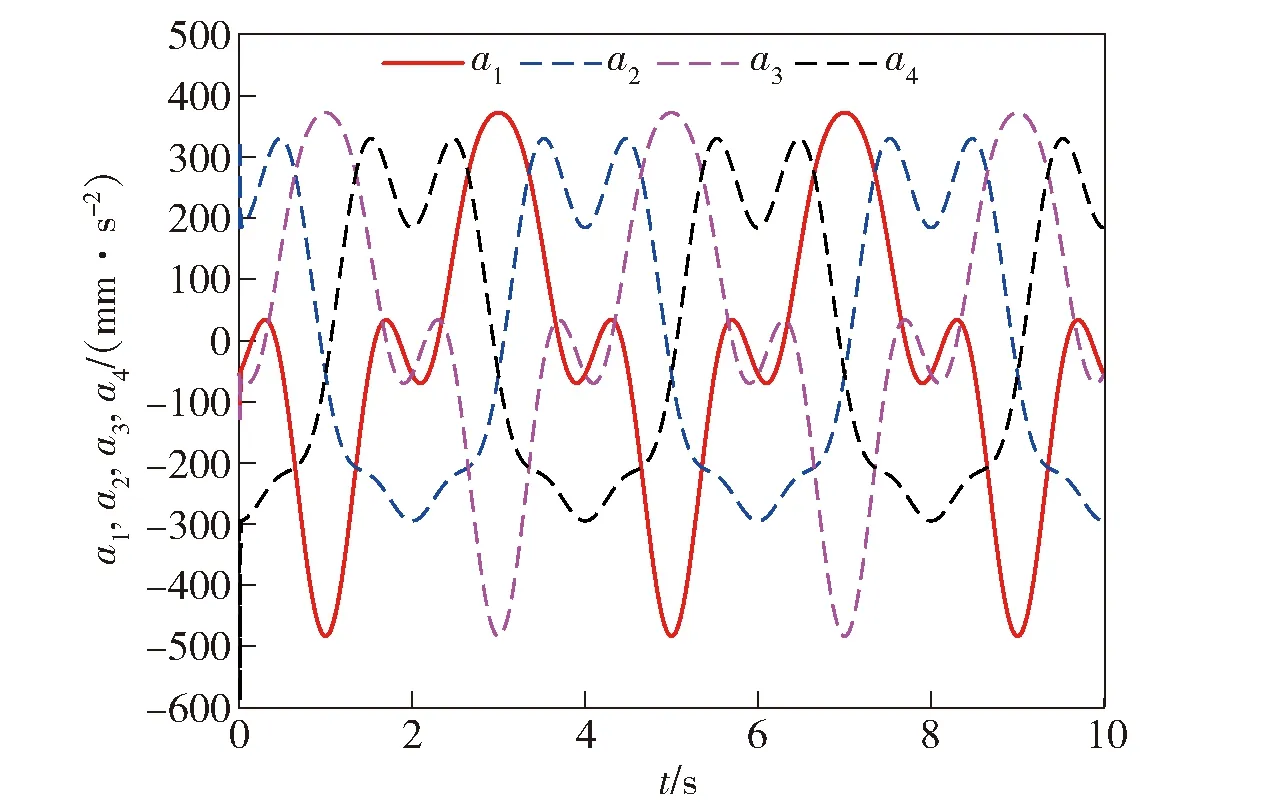
图12 4条绳驱动支链的加速度理论仿真曲线Fig.12 Simulated acceleration curves of four cable-driven chains
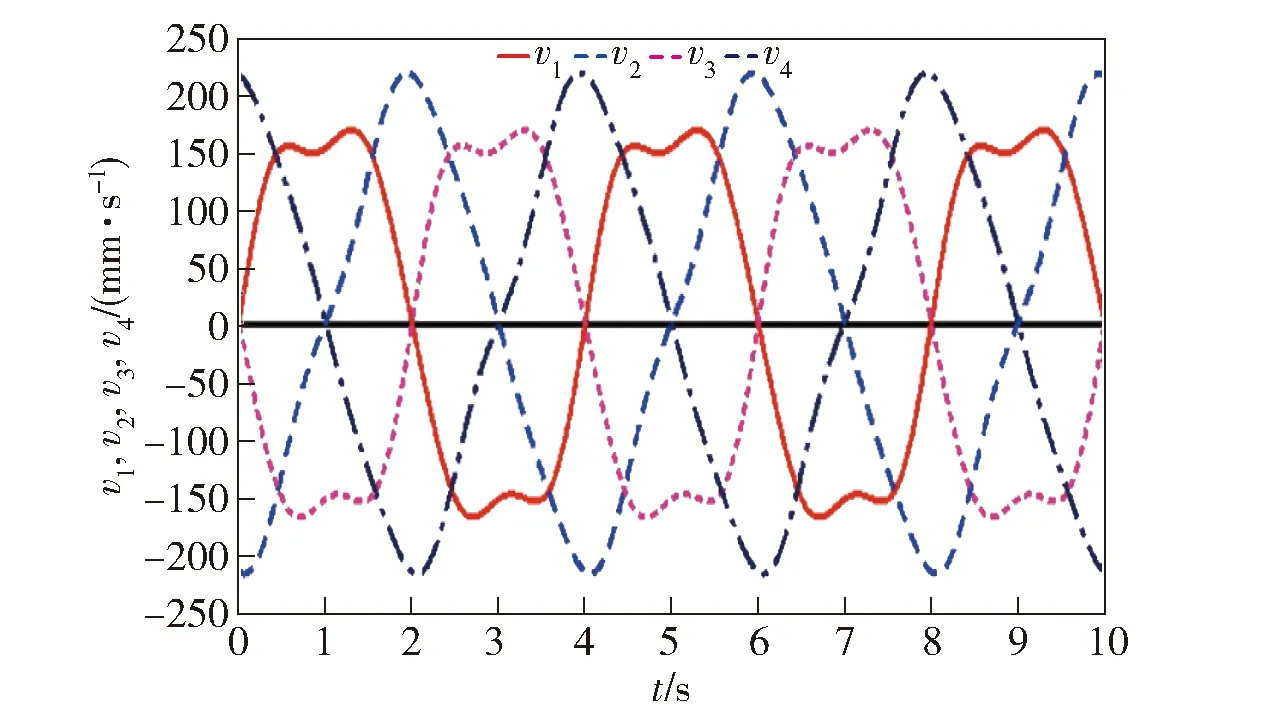
图13 4条绳驱动支链的速度Adams仿真曲线Fig.13 Simulated velocity curves of four cable-driven chains by Adams

图14 4条绳驱动支链的加速度Adams仿真曲线Fig.14 Simulated acceleration curves of four cable-driven chains by Adams
经以上分析可知,基于矢量封闭方法求出逆解方程,逆解方程两边对时间求导法对绳驱动4-SPS/U刚柔并联式躯干关节机构的瞬时运动学进行理论上分析的结果,与利用 Adams 软件进行仿真分析的结果相吻合,验证了本文基于弹簧的绳驱动4-SPS/U刚柔并联式躯干关节机构运动学建模方法的正确性,且设计的绳驱动刚柔并联式机构具有较大的偏转范围,能够调整姿态多样化。
6 结论
本文采用将绳驱动并联机构中添加刚性过约束支链的思路,创新设计了一种绳驱动4-SPS/U刚柔并联式躯干关节机构。利用矢量封闭方法构建了躯干关节机构的运动学逆解模型,通过对运动学逆解方程进行时间求导建立了速度、加速度运动模型以及雅克比矩阵,并分析出该机构不存在奇异位形。得到主要结论如下:
1)运用螺旋理论自由度求解方法验证了该躯干关节机构能够实现绳驱动2自由度的转动。说明了多运动模式6足移动机器人可以通过该躯干关节机构实现少自由度的空间位姿变化,从而证明了该躯干关节机构能够使机器人具备了行走、水中推进、攀爬以及滚动等多种运动模式的姿态多样性。
2)通过数值算例计算了绳驱动支链的位移、速度和加速度理论仿真数据,并将理论仿真数据与Adams软件仿真数据进行了对比,从而验证了该机构理论模型的正确性。
3)基于该机构的工作空间仿真分析,证实了绳驱动4-SPS/U刚柔并联式躯干关节机构具备运动灵活、运动工作空间大及工作空间内无奇异位形等姿态运动特点,能够保证多运动模式6足移动机器人在各种不同环境中灵活实现多种运动模态的姿态调整要求。
