高超声速飞行器鲁棒多目标线性变参数控制
2019-12-23蔡光斌赵阳张胜修杨小冈
蔡光斌, 赵阳, 张胜修, 杨小冈
(1.火箭军工程大学 导弹工程学院, 陕西 西安 710025; 2.西北工业大学 航天学院, 陕西 西安 710072)
0 引言
高超声速技术被称为21世纪航空航天技术的“制高点”[1-2],其是当前以及未来航空航天领域发展的核心技术之一[3],特别是具有“乘波体”构型的吸气式高超声速飞行器,被认为是一种未来进入太空更经济有效的方式,因其重要的战略意义而备受世界各军事强国的广泛关注[4]。
吸气式高超声速技术的发展始于20世纪50年代提出的高超声速燃烧概念[2-3]。经过几十年的发展,美国、俄罗斯、法国、德国、英国、日本和印度等国自20世纪90年代以来已在高超声速技术方面陆续取得了重大进展,并相继开展了多项地面试验和飞行试验[3-5]。目前,高超声速技术已经从早期的概念和原理探索阶段进入到以高超声速巡航导弹、高超声速飞机和空天飞机等为应用背景的先期技术开发阶段和工程研制阶段。对于高超声速飞行技术的研究,我国起步较晚,在21世纪以前,我国的研究主要集中于基础性的研究。2014年,我国自主完成首次高超声速风洞实验,结束了60多年的国外技术垄断[4-9]。近年来,我国正在紧锣密鼓地进行“乘波体”高超声速飞行器的自主研制和飞行试验工作,并取得了一系列的突破性进展。
与传统的飞行器相比,吸气式高超声速飞行器由于采用超燃冲压发动机、机体/发动机一体化设计技术,导致其气动特性、推进系统与结构动态之间存在明显的耦合效应[6-9];同时,高超声速飞行器的飞行包线范围更大,飞行环境更加复杂,存在各种随机干扰和扰动,使控制系统随飞行区域的变化呈现出强烈的非线性和严重不确定性[10];此外,由于高超声速飞行器的快速飞行,使得其所携带的燃料迅速消耗,从而引起高超声速飞行器的质量分布快速变化,使高超声速飞行控制系统具有明显的快时变性[3]。因此,高超声速飞行控制系统具有强非线性、强耦合性、快时变性以及严重的不确定性。
目前,国内外学者在高超声速飞行器的飞行姿态控制技术方面已取得了一系列的研究成果,从控制方法角度出发,可分为以下3类:基于线性模型的控制方法、基于非线性模型的控制方法、基于线性参变/时变模型的控制方法。文献[11-12]所采用的控制方法就属于第一类控制方法,该类方法对模型的精度要求较低,有利于系统的稳定性分析与控制性能设计,但对于具有快时变、强耦合、强非线性以及严重不确定性的高超声速飞行控制系统而言,一般基于线性化的控制设计方法均存在着不同程度的局限性。例如:现有的线性控制设计一般只是基于系统的某个平衡工作点附近的线性化模型来设计局部控制器,而对于非平衡点处或者非设计区域无法实现对飞行器的大跨度机动飞行控制;文献[13-14]所采用的控制方法属于第二类控制方法,该类方法更加符合高超声速飞行控制系统的非线性模型本质,但对模型的结构和精确性要求更高,且不易做鲁棒性分析。这对于具有较强的参数与结构不确定性和未建模动态的高超声速飞行器控制系统设计而言,限制了许多非线性方法的应用。例如,许多非线性控制设计是基于反馈线性化模型展开的,但是对于大多数高超声速飞行器模型而言,通常不满足反馈线性化条件的,一般都是加入多个较强的假设条件才能实现反馈线性化。然而,即便是对可反馈线性化的系统,反馈线性化后得到的高阶李导数求解过程和表达式都极为复杂,后续设计过程中无法在此基础上展开诸如鲁棒性、自适应性等控制性能分析[15]。
基于线性参变模型的控制方法实质上是利用线性控制方法对非线性系统进行控制器设计,其最大优点是控制器本身为参数依赖,可以进行自增益调节,而且鲁棒稳定性可以从理论上得到保证,如文献[16-23],都属于该类控制方法,因此本文采用该类控制方法设计高超声速飞行器姿态控制系统。
对于具有快时变、强耦合、强非线性、严重不确定性的高超声速飞行控制系统而言[3],所设计的控制器必须具备鲁棒稳定性、干扰抑制能力和一定的动态跟踪特性。H∞控制器在系统出现不确定性时具有较好的鲁棒稳定性,但这是以牺牲其他指标为代价的,最终的控制系统性能仍难以满足要求[17];而H2性能对于处理随机噪声、干扰很有效,但控制效果完全依赖于描述被控对象数学模型的精确性,这点影响了传统H2最优控制器在实际中的应用[18];极点配置通过将闭环系统的极点配置到指定区域内,就能保证系统具有一定的动态特性[21]。因此,本文在得到吸气式高超声速飞行器刚性线性变参数(LPV)模型的基础上,针对其纵向飞行姿态控制问题,提出了一种基于区域极点配置的H∞/H2多目标LPV控制系统设计方法,较之传统的H∞控制器与H2控制器,该方法对控制系统模型的精确性要求不高,且不仅可以保证闭环系统的稳定性,而且还使所设计的跟踪控制器具有较好的鲁棒性和动态特性;同时,通过引入松弛变量,降低了所设计控制器的保守性。最后通过与现有文献[23]中的方法进行仿真对比,说明了所设计控制器的有效性和优越性。
1 纵向LPV建模
1.1 吸气式高超声速飞行器纵向机理模型
吸气式高超声速飞行器纵向平面的详细几何尺寸可以参照文献[3-4,7]。根据普朗特- 迈耶尔理论,应用拉格朗日方程,可以得到吸气式高超声速飞行器纵向非线性机理模型[3-4]:
(1)
式中:v为飞行速度;h为飞行高度;α为攻角;γ为飞行路径角;Q为俯仰角速率;T、D、L、Myy分别表示推力、阻力、升力、俯仰力矩;m为飞行器质量;μ为地球引力常量;r为飞行器质心到地心的距离;Iyy为俯仰转动惯量。上述各力与力矩系数以及相应的气动力与力矩系数表达式为
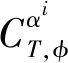
1.2 刚性LPV模型
针对机理模型(1)式,忽略飞行器的弹性效应,在后续的控制器设计中,将其视为模型的不确定性[3-4]。为了得到LPV模型,首先选取调度变量θ=[Ma,h]T,在马赫数Ma∈[8,10],飞行高度h∈[24 672,30 840]的飞行包络内进行网格划分,并对网格上的每个点进行配平得到平衡状态点,从而得到围绕平衡状态的增量模型,然后采用雅克比结合张量积的方法可以得到具有多胞结构的刚性LPV模型,模型转化的具体过程和主要思路参见文献[20]。这里,给出增量形式的LPV模型如下:
(2)
式中:xν=[vν,hν,αν,γν,Qν]T代表飞行状态围绕平衡状态的增量,vν、hν、αν、γν、Qν分别为飞行速度、飞行高度、攻角、飞行路径角、俯仰角速率围绕平衡状态的增量;uν=[δeν,δcν,φν,Adν]T代表控制变量围绕平衡状态的增量,δeν和δcν分别为升降舵偏角和鸭翼舵偏角围绕平衡状态的增量,φν为等效燃料率的增量,用于控制发动机推力大小,Adν为扩散区比例的增量,用于控制发动机的进气量,从而间接控制推力;A(θ)、B(θ)分别为
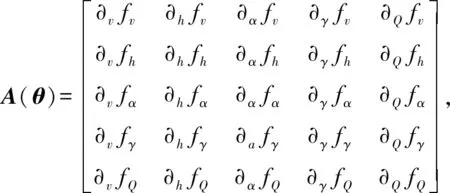
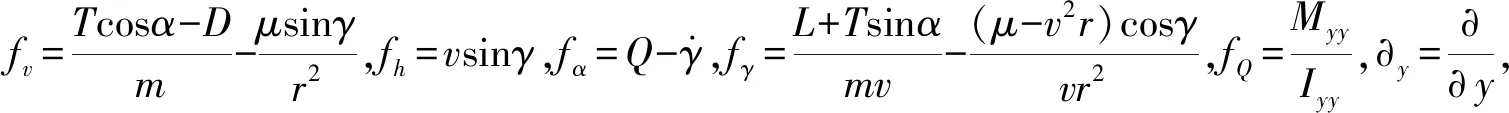
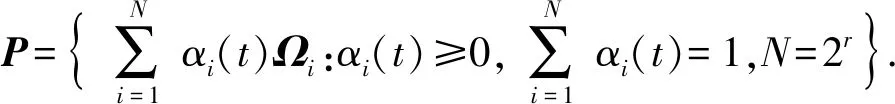
注释1在后续内容中,将针对上述高超声速飞行器的多胞LPV模型进行控制器设计。下节中,将考虑更一般化的多胞LPV系统,提出连续时间多胞LPV系统的变增益H∞/H2控制器设计理论方法。其中,将在一般化的多胞LPV系统中引入了干扰输入量,这类干扰输入可以作为高超模型和参数不确定性、高超弹性模态影响等输入项。
2 基于区域极点配置的混合多目标LPV状态反馈控制
2.1 问题描述
考虑如下多胞LPV系统S:
(3)
式中:A(θ)、Bi(θ)、Ci(θ)、Di(θ)均为LPV系统S的相容矩阵;x∈Rn为状态向量,w∈Rl为干扰输入,u∈Rm为控制输入,z∞∈Rn1为H∞性能指标下的控制输出,z2∈Rn2为H2性能指标下的控制输出,n、l、m、n1、n2表示向量维数且相容。针对LPV系统S,设计如下状态反馈控制律:
u=K(θ)x,
(4)
式中:K(θ)∈Rm×n. (4)式代入到(3)式中,可以得到如下闭环LPV系统CDOF:
(5)
式中:系数矩阵Acl(θ)、C1cl(θ)和C2cl(θ)分别为
Acl(θ)=A(θ)+B2(θ)K(θ) ,
(6)
C1cl(θ)=C1(θ)+D12(θ)K(θ),
(7)
C2cl(θ)=C2(θ)+D22(θ)K(θ).
(8)
问题1针对(3)式中的多胞LPV系统S,设计形如(4)式中的LPV状态反馈控制器,使得(5)式中的闭环LPV系统CDOF对所有的调度参数满足如下特性:
1)稳定性能:系统的闭环极点配置到复平面左半平面上指定的圆形线性矩阵不等式(LMI)区域(如图1所示,LMI区域的具体定义详见参考文献[21-22]),使Acl(θ)稳定;同时使闭环系统CDOF具有一定的动态性能。
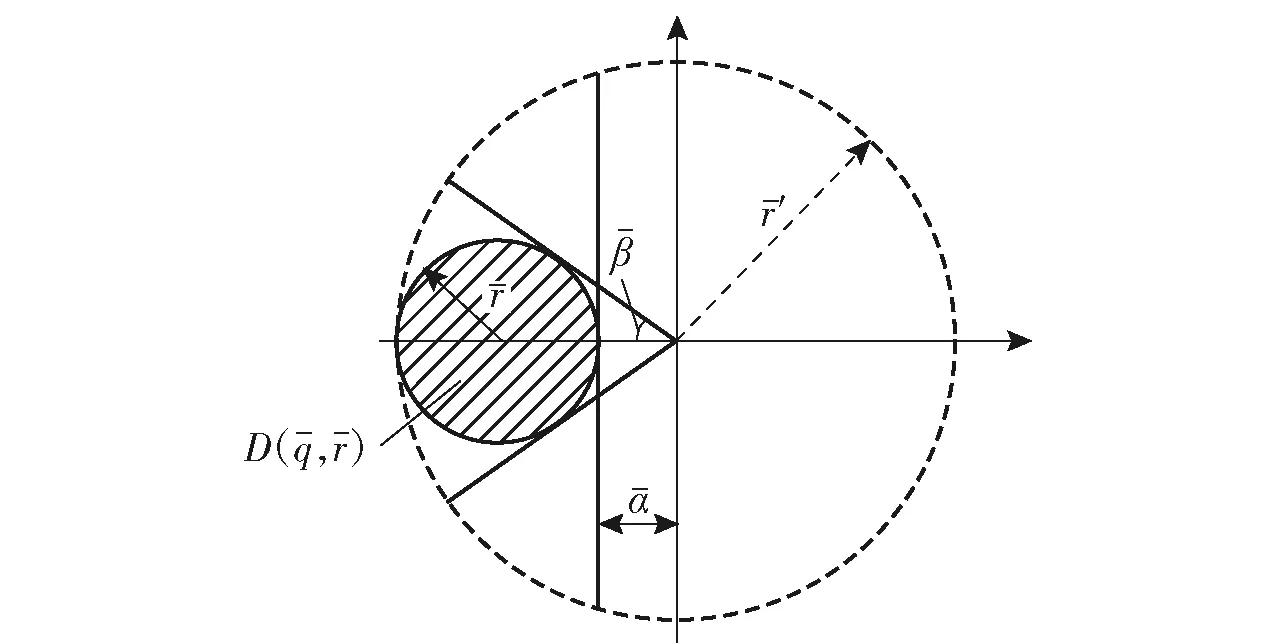
图1 圆形LMI区域Fig.1 Circular region of LMI[21-22]
2)H∞性能[22]:对于能量有界输入信号w∈L2,给定性能指标γ>0,使得由w到z∞的传递函数矩阵Tz∞w(s)的H∞范数|Tz∞w(s)|∞<γ.
3)H2性能[22]:对于随机干扰输入信号w,给定性能指标η>0,使得由w到z2的传递函数矩阵Tz2w(s)的H2范数满足|Tz2w(s)|2<η.
2.2 基于区域极点配置的H∞/H2LPV控制
为了解决问题1,首先给出如下引理:
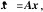
(9)
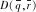
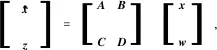
(10)
式中:*表示由对称矩阵的对称性得到的块矩阵(以下情形类似,不再重复说明)。
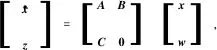
(11)
(12)
trace(Q)<η2.
(13)
引理4[16]下列条件等价:
2)存在矩阵G使得下式成立:
通过引入松弛变量G,使得在变量和约束增维的空间中,产生了扩展条件,可以实现Lyapunov函数矩阵与系统矩阵解耦。
根据文献[23]中的思想,易将引理1~引理3从LTI系统推广到多胞LPV系统,结合问题1,给出如下定理:
定理1针对(3)式中的多胞LPV系统S,给定正标量γ>0和η>0,存在形如(4)式中的增益调度状态反馈控制器,使得闭环系统CDOF满足问题1中3个特性的充分条件为存在正定对称矩阵X,对称矩阵Q和矩阵Li,i=1,…,N,j=1,…,N,假设各矩阵之间维数是相容的,且满足如下LMI约束条件:
trace(Q)<η2,
(14)
(15)
(16)
(17)
(18)
(19)
Ξij=
(20)
若(14)式~(20)式有解,则状态反馈调度增益K(θ)可由(21)式求得:
(21)
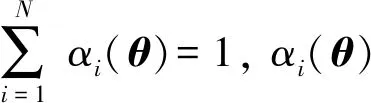
证明(6)式~(8)式中的闭环系数矩阵代入(9)式、(10)式和(12)式的左边,分别得:
(22)
(23)
(24)
令XD=X∞=X2=X,并引入新的矩阵变量L(θ):
(25)
根据LPV系统的多胞特性, (22)式~(24)式可分别化为
Γ(θ)=
(26)
(27)
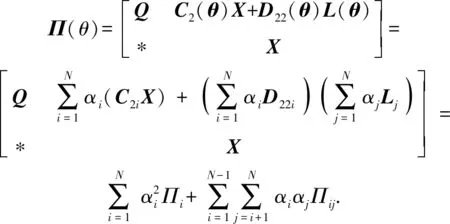
(28)
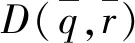
注释2定理1由于计算简单,计算量小,能简化系统分析与综合过程,所以应用起来很方便。同时注意到定理1中的LMI约束不仅仅对矩阵X、Q和矩阵Li是线性的,而且也是性能指标γ和η的线性约束,因此,定理1的求解条件就可转化成具有LMIs约束的线性目标函数最小化问题。然而,在实际应用中,性能指标γ与η不可能同时达到最优,必须进行加权处理,常见的加权形式如下:
J=aγ+bη,
(29)
式中:a、b为权值,可以根据具体的设计要求进行设定。于是,定理1的求解条件变为
(30)
由定理1的证明过程可知,此定理实际上限制了XD=X∞=X2=X,而且还要求在所有的多胞顶点上只存在一个共同的Lyapunov函数矩阵,显然,这给系统的综合带来了较大的保守性。对此,可以通过引入松弛变量的方法来降低保守性,即提出定理2如下。
定理2针对定理1中的设计要求,其可行的充分条件为存在正定对称矩阵X∞i、X2i,正定矩阵XDi,对称矩阵Qi和矩阵G1、G2、H1i、H2i,i=1,…,N,假设各矩阵之间维数是相容的,且满足如下LMI约束条件:
trace(Qi)<η2,
(31)

(32)
(33)
(34)
(35)
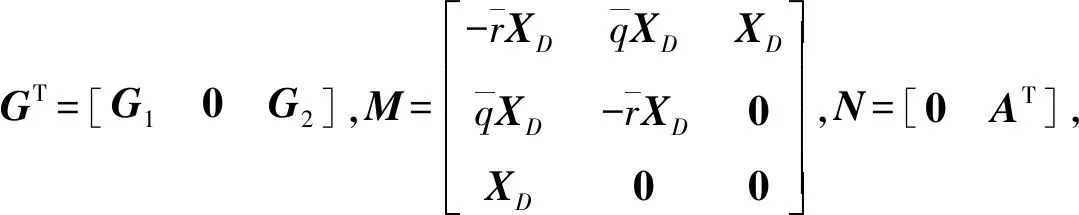
(36)
令
根据引理4,(12)式等价于(37)式:
(37)
令
(38)
根据引理4,(13)式和(14)式分别等价于(38)式:
(38)
(39)
由于问题1面向的是多胞LPV系统,根据凸优化理论可知,只要针对多胞的顶点进行控制器设计即可,于是,(6)式~(8)式在多胞模型顶点的表达形式为
Aicl=Ai+B2iKi,
C1icl=C1i+D12iKi,
C2icl=C2i+D22iKi.
(40)
(40)式带入(36)式~(39)式中,并引入新的矩阵变量H1i=KiG1,H2i=KiG2,i=1,…,N,即可得到(31)式~(35)式的LMI约束条件。证毕。
注释3定理2通过引入松弛变量,使Lyapunov函数矩阵与系统矩阵解耦,从而可以在不同的顶点上使用不同Lyapunov函数矩阵,降低了控制系统设计的保守性,但由于存在着KiG1和KiG2等矩阵变量的耦合项,因此是一个双LMI求解问题,不能直接利用Matlab中的LMI工具箱进行求解,解算难度增大,计算量相对于定理1也大大增加,具体解法可参见文献[24]。
注释4由于KiG1和KiG2等矩阵变量之间存在着耦合项,其并不是LMI的典型形式,不能直接使用LMI工具箱求解。采用文献[25-27]提出的锥互补线性化算法,可将其转化为一些受LMI约束的序列优化问题来解决。故由锥互补线性化算法可将定理2中的求解条件转化为如下所示的受LMI约束的最小优化问题:
(41)
若受LMI约束的最小优化问题(41)式可解,则定理2中的条件也是可解的,虽然不一定存在全局最优解,但是此最小优化问题也比双线性不等式的求解过程容易得多。
3 数值仿真算例
3.1 控制器设计
应用第2节提出的基于区域极点配置的H2/H∞控制系统设计方法,来实现吸气式高超声速飞行器的跟踪控制。首先,参照文献[20]中的方法,将(2)式中的刚性LPV模型扩展成系统设计所需的(3)式的形式。
重新书写(2)式中的状态方程,表达形式如下:
(42)
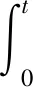
式中:xv表示参考输入速度信号rv(τ)与实际速度v(τ)之差的积分;xh表示参考输入高度信号rh(τ)与实际高度h(τ)之差的积分,以此扩展开环系统的状态变量。
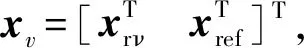

A(θ)xν+Bw(θ)w+Bu(θ)uν.
(43)
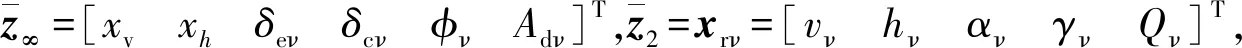
Cz∞xν+Dz∞uν,
(44)
(45)
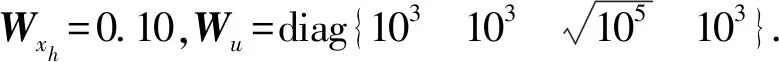
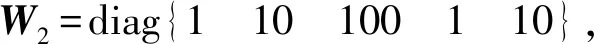
(46)
z∞=C1(θ)x+D12(θ)u,
(47)
z2=C2(θ)x,
(48)
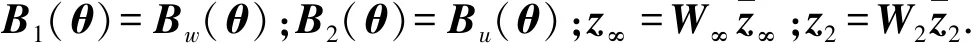
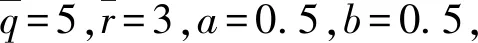
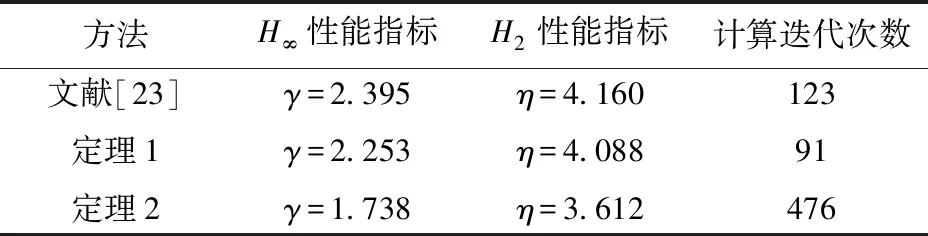
表1 鲁棒性能指标
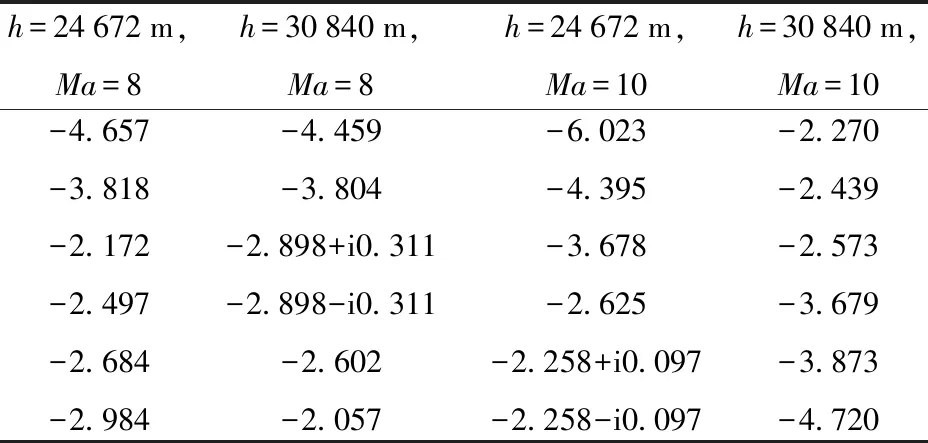
表2 各顶点的闭环极点
通过表1可以发现,定理1得到的两个性能指标与采用文献[23]中方法得到的性能指标相比很接近,降低幅度不大,但定理2得到的两个性能指标都小于前两种方法得到的,因此,可以验证定理2确实降低了控制系统设计的保守性;同时,还可以看出,定理1的计算迭代次数是最少的,更适合实际工程应用,定理2的计算迭代次数明显多于前两种方法的迭代次数,而且计算结果还依赖于初值的选取,但对于目前计算机的计算速度来讲,是能够接受的。从表2可以看出,各顶点的闭环极点都配置到了圆形区域D(5,3)中,由多胞性质可知,刚性LPV系统的所有闭环极点都位于圆形区域D(5,3)中,可以使系统具有良好的动态特性。
为了综合求解上述的问题,首先将系统(2)式转化为多胞形式。参数依赖的系统矩阵A(θ)和B(θ)可以表示为

根据各顶点状态反馈控制器K1、K2、K3、K4,可以得到刚性LPV模型增益调度状态反馈控制器K:
K(Ma,h)=α1K1+α2K2+α3K3+α4K4.
(49)
3.2 非线性仿真与结果分析
为了验证上述所设计控制器的有效性,基于Matlab/Simulink仿真环境,在h=26 518 m,Ma=8.8的平衡巡航条件下(Ma=8.8,v=26 353 m/s,α=1.47°,Q=0°/s,h=26 518 m,γ=0°,δe=11.953°,δc=-0.62°,φ=0.338,Ad=0.84)进行非线性仿真。
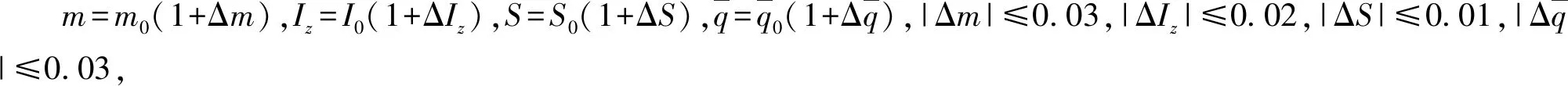
参考输入信号rv(t)和rh(t)的形式[4]如下:
仿真结果如图2、图3所示。
图2(a)、图2(b)分别给出了在采用本文方法(定理1)与传统方法(参考文献[23])所设计控制器的作用下,标称模型和引入参数不确定性后模型的速度和高度响应曲线。由图2(a)、图2(b)中可知,对于任一种模型,采用本文定理1所设计的控制器都能在6 s内跟踪到参考指令输入,而标称模型在参考文献[23]中传统方法所设计控制器的作用下,需要10 s左右的时间才能跟踪到参考指令输入,且具有最大不确定参数模型的调节时间更长,因此采用定理1所设计控制器的动态性能要比采用参考文献[23]中方法所设计控制器的动态性能好。两种模型在采用定理1所设计控制器的作用下都能够准确地跟踪到参考指令输入信号,同时,通过比较采用定理1所设计控制器作用下的两种曲线可以发现,具有最大不确定参数模型的阶跃响应比标称模型的阶跃响应调节过程长,且还出现了一定的超调,但都在合理范围之内。此外,在进行非线性仿真过程中,引入了一定的外界干扰,但仿真结果中没有出现被干扰的现象,因此说明所设计的控制器还具有较强的抗干扰能力。
图2(c)~图2(e)为其他状态量在参考指令输入信号作用下的变化曲线,从中可以看出,它们的大小均在有效范围内变化,并且很快地趋近稳定。
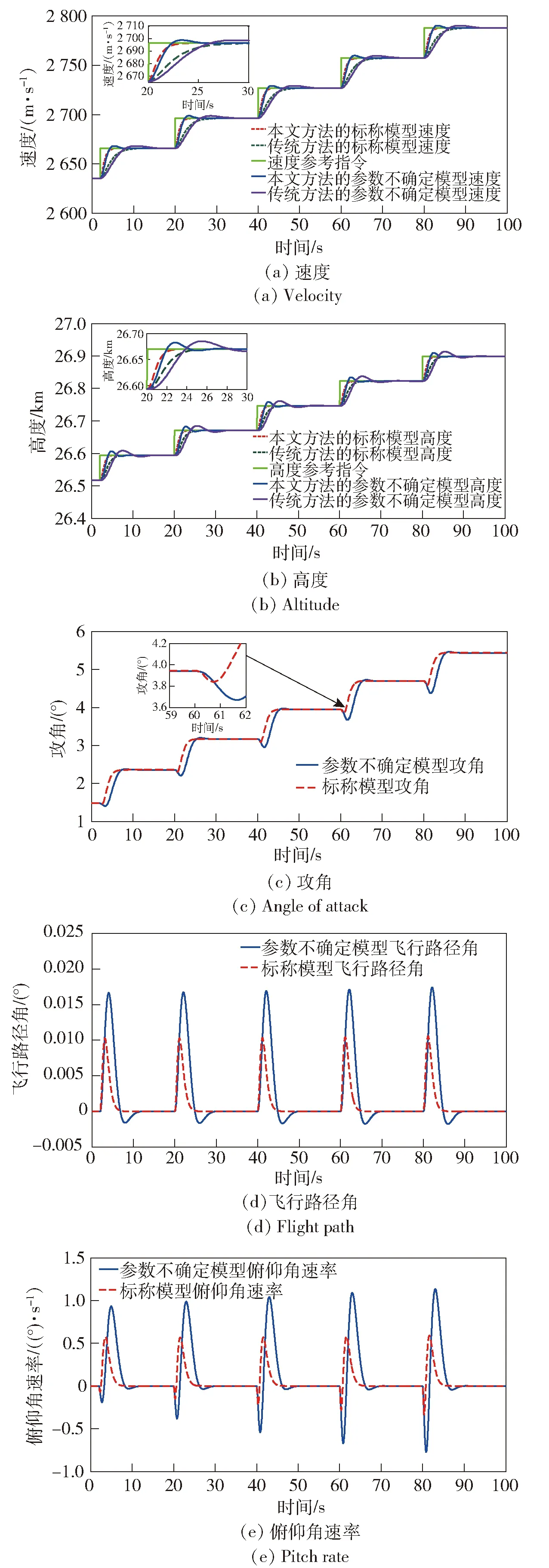
图2 速度跟踪下的状态阶跃响应Fig.2 Step response of speed tracking
图3(a)和图3(b)为两个舵偏角控制输入的变化曲线,从中可以看出,输入变量均在有效地范围内变化,并且很快地趋近稳定,说明所设计的控制器能够保证执行机构不会达到饱和效应。图3(c)和图3(d)分别为等效燃流率和扩散区比率的变化曲线。这两个控制输入的调节都会影响到发动机推力的变化。从图3(c)可以看出,每当阶跃输入作用在闭环系统上时,等效燃流率都会迅速增加,最终趋于稳定值,其控制作用直接影响到高超声速飞行器的实际速度与高度变化,实现了速度和高度的跟踪控制。从图3(d)可以看出,扩散区比率的变化曲线随着阶跃输入信号的一次次升高而一次次的降低,最终达到稳定值,这正说明随着飞行速度和高度的增加,高超声速飞行器的发动机会自动调节扩散区比率的大小,来保证进入到燃烧室内的压缩空气具有一定的速度,从而保证了发动机的正常工作。
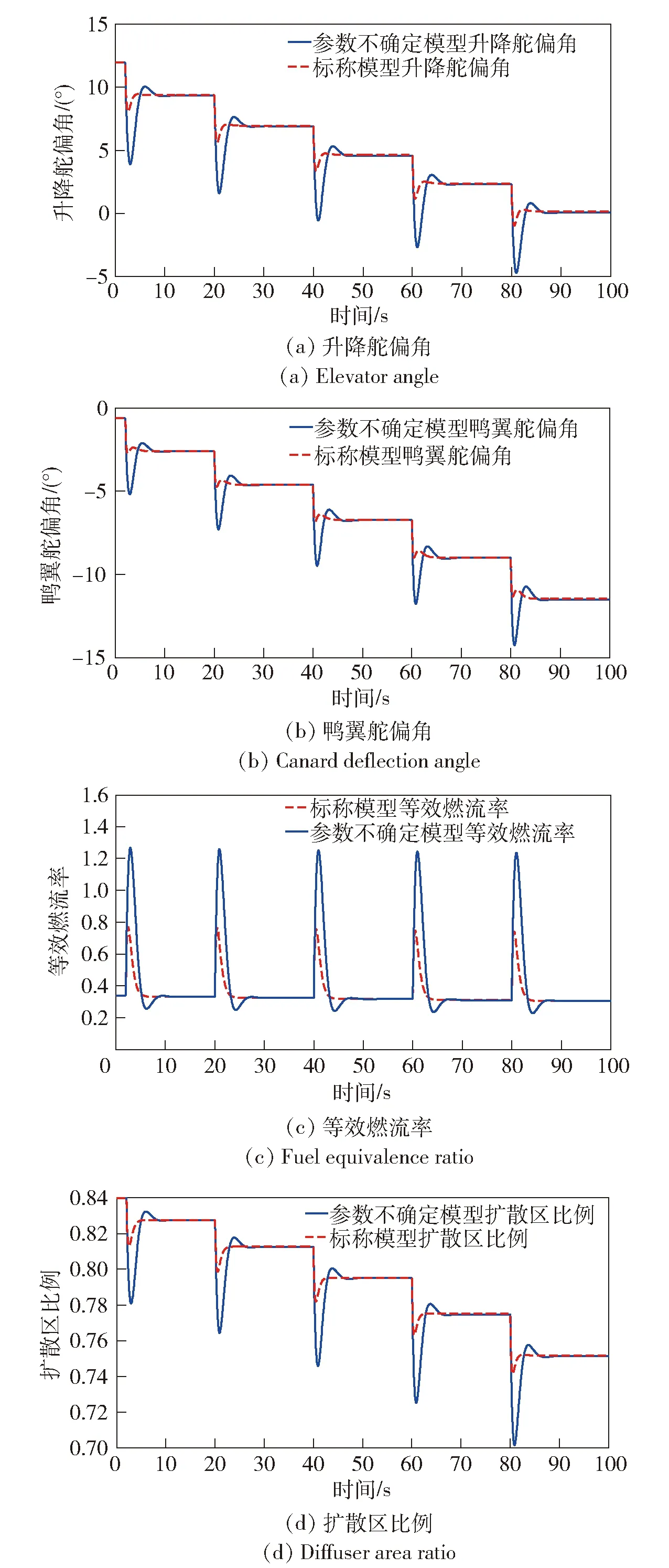
图3 速度跟踪下的控制输入阶跃响应Fig.3 Step response of control input of velocity tracking
4 结论
1) 针对吸气式高超声速飞行器的纵向飞行控制,本文建立了具有多胞结构的刚性LPV模型。针对此类模型,提出了一种基于区域极点配置的H∞/H2多目标LPV状态反馈鲁棒控制算法,通过理论上的严格推导,证明了此算法能够实现系统的多目标控制。
2) 通过引入松弛变量的方法,降低了控制系统设计的保守性,最终得到了满足期望性能指标要求的LPV状态反馈鲁棒跟踪控制器。
3) 所设计的控制器应用在高超声速飞行器非线性机理模型上,通过仿真验证了所设计的控制器有效性,实现了吸气式高超声速飞行器的自增益稳定飞行控制。
