基于Bayes小子样理论和序贯网图检验的武器装备测试性验证试验方案设计
2019-12-23王康史贤俊秦亮聂新华龙玉峰
王康, 史贤俊, 秦亮, 聂新华, 龙玉峰
(海军航空大学, 山东 烟台 264001)
0 引言
测试性是指装备能及时准确的确定自身状态,并能有效隔离其内部故障的一种重要设计特性[1]。随着测试性技术的发展,一些装备中已逐步采纳了测试性设计的思想,并在保障装备的正常工作和良好性能中逐渐体现出其重要作用。而如何科学合理的评价装备测试性水平则成为了科研人员研究的一个重要问题。
测试性验证试验的开展是用于检验故障检测率(FDR)和故障隔离率(FIR)等测试性指标是否满足规定的指标要求值,主要实施方法是通过在测试性样机中采取人工注入故障的方式,并根据其检测/隔离情况对装备进行接收/拒收判断[2]。一个完整的测试性验证试验包括计算模型的选择、样本量确定、样本选取、故障注入以及指标评估等相关技术组成[3]。由于故障注入试验的结果为成败型数据,因此当前测试性验证试验方案的计算模型主要基于二项分布模型。同时,故障样本量确定作为整个测试性验证试验的首要环节,如何在约束条件下保证测试性验证所需样本量科学合理,并使确定的样本量尽可能小,是当前需要解决的核心问题。
当前确定样本量的经典方法为单次抽样方法,即在承制方、使用方测试性水平以及双方风险的约束下,寻求一个最佳的样本量以及对应允许的最大检测/隔离失败数的过程[4]。但随着科技日新月异的发展,武器装备结构日益复杂,导致其造价高昂,投试使用的样机减少,装备全寿命周期加长,导致试验样本量受到小子样条件的限制。而通过经典验证方法确定的样本量较大,进而实施故障注入危害性高,会对装备造成损伤,导致试验代价高昂。基于此,Wald[5]提出了一种序贯概率比检验(SPRT)方法,该方法无需在验证试验开展前预先指定样本量,可通过实际验证试验结果以序贯方式动态地确定样本量。同时,Wald和其学生证明了在相同的约束条件下,SPRT方法较之单次抽样方法、二次抽样方法和多次抽样方法所需平均样本量小[6]。但是由于通过SPRT方法确定样本量无法事先控制,也无法进行预算,对此文献[7]在给出序贯检验优化设计模型的基础上,采用Monte Carlo随机模拟方法对战术导弹序贯检验和序贯截尾检验方案进行了优化,对试验次数进行了初步预算;文献[8]在已有序贯检验方法的基础上,针对检验边界为动点的截尾序贯设计方案进行了改进;文献[9]提出了基于序贯网图检验(SMT)的维修性试验评定方法,结果表明该方法可有效减少试验样本量同时能克服SPRT方法无法预测样本量的不足,给出试验的最大样本量限制。以上方法均在一定程度上降低了试验样本量,同时也限制了试验的无限制进行,但是对于导弹等这类高成本、高精度的武器装备的验证试验问题,通过以上截尾措施所确定的故障样本量仍然较大,无法满足实际需求。
在装备生产研制过程中,存在大量的先验信息,但实际验证试验却受到小子样条件的限制,Bayes方法常用于小子样情况下试验结果的分析与评估[10-11]。其主要原因是,Bayes方法除能运用当前验证信息外,还能有效融合装备在设计各阶段的先验信息,达到减少样本量的目的,进而推动了Bayes小子样理论在可靠性[12]、维修性[13]以及测试性[14-15]等领域的广泛应用。文献[16]在小子样条件下通过考虑未知分布参数的先验信息,提出了一种基于验前信息的序贯验后加权检验(SPOT)方法,能有效运用验前信息并结合少量试验数据对装备可靠性进行评定;文献[17]采用SPOT方法检验对数正态分布中的未知参数,通过平均维修时间(MTTR)阈值的确定,实现样本量的计算;文献[4]以二项分布模型为前提,利用SPOT方法开展测试性验证试验方案制定,结果表明通过SPOT方法确定的测试性验证样本量要比SPRT方法小。以上方法均在Bayes框架下对SPRT方法进行了扩展,并根据不同领域问题针对性进行研究,通过进一步综合相关文献中对SPOT方法的研究,发现仍存在截尾策略选取导致求解方案的复杂性以及验证样本量确定后缺乏对决策合理性的进一步分析问题。
鉴于以上分析,SMT方法是SPRT方法的一种有效扩展,一方面较之SPRT方法确定的样本量少,另一方面SMT方法易于求解验证试验的截尾样本量,同时综合考虑Bayes小子样理论能充分利用先验信息达到降低样本量的优势,故本文提出一种基于Bayes小子样理论和序贯网图检验(BSST-SMT)的测试性验证试验方案设计方法。在Bayes框架下实现对SMT方法的有效扩展,旨在充分运用Bayes小子样理论对先验信息利用的优势以及SMT方法的优点,通过对测试性验证指标——FDR/FIR的插入点选择,划分指标参数空间,并进行相应检验,进而确定截尾样本量,在综合考虑双方实际风险值基础上得到小样本量的测试性验证试验方案。
1 测试性验证研究基本方法
1.1 测试性指标约束参数
在装备测试性验证过程中,由于故障注入是成败型试验,故选取二项分布计算模型,进行试验判决需要考虑的测试性指标约束参数有:承制方要求值p0,使用方要求值p1,承制方风险α以及使用方风险β,用以表征装备测试性水平。
1.2 经典验证方法
经典验证方法确定故障样本量采取单次抽样的方法,其抽样特征函数可表示为
(1)
式中:p表示测试性指标;n表示验证样本量;c表示样本量n下的最大允许检测/隔离失败次数;f表示实际观测到的失败次数。
对于FDR/FIR验证试验,当注入n个故障后:如果检测失败数f≤c,则认为FDR/FIR验证通过;若f>c,则认为FDR/FIR未通过验证,需要对测试性设计进行改进。
研究表明经典验证方法能在验证试验开展前确定故障样本量,但是所确定的故障样本量过大不利于工程实现。
1.3 SPRT方法
针对经典验证方法所确定故障样本量过大的问题,将测试性指标约束参数转化为假设检验问题,指标参数空间划分为Θ=Θ0∪Θ1,其中Θ0={p0},Θ1={p1},对应的简单假设为
H0:p=p0,H1:p=p1.
(2)
假设n次验证试验结果序贯序列表示为X={X1,…,Xi,…,Xn},式中Xi取值为0或1,Xi=1表示故障检测/隔离成功,Xi=0表示故障检测/隔离失败,记c为n次试验结果序贯序列中Xi=0的个数,即表示累积验证失败次数。则两种假设似然函数比[18]为
(3)
定义λn判决阈值上界为B,下界为A,则相应的接受/拒收判决可由λn与A、B的大小关系所确定。
同时,Wald[5]给出了当p0和p1相差不大时SPRT方法的近似抽样特性解析表达式:
(4)
式中:Lp表示在测试性指标p下的抽样特性函数;参数h表示以下等式的非零解为
(5)
同样给出了SPRT方法的近似平均抽样次数Ep(n)的解析表达式如下:
(6)
SPRT方法下样本量是一个随机变量,故通常选择平均样本量Ep(n)作为度量指标,在相同指标约束下,其平均样本量小于经典验证方法所得的样本量。但是也正是由于SPRT方法样本量的随机性,导致其最大样本量不可控,缺乏最大样本量的SPRT方法会导致验证无法实施。
2 基于BSST-SMT的测试性验证试验方案设计
在序贯验证试验方案设计中,度量指标除了要求验证试验所需平均样本量小之外,其最大样本量也是需要考量的重要因素,截尾SPRT方法虽然具有最大样本量,但所确定的最大样本量仍然较大,不能满足实际验证试验需求;SMT方法是在SPRT方法的基础上,通过插入一系列检测点,实施对检验问题拆分,有效实现对最大样本量的控制,相对于SPRT方法而言,能克服SPRT方法无法控制验证试验所需样本量的不足,且具备比截尾SPRT方案更小的最大样本量,改进效果明显,但对于导弹武器装备而言,所确定的样本量仍存在过大的情形。结合SPOT方法对于先验信息利用的思想,考虑BSST能有效处理各类先验信息,提出一种基于BSST-SMT的测试性验证试验方案设计方法,主要涉及下述6个方面的内容。
2.1 指标参数空间划分
BSST-SMT方法与SMT方法一样,是在SPRT方法的基础上,在给定的指标参数空间中插入m-1个点,实现参数空间的重新划分,即Θ=Θ0∪…∪Θi∪…∪Θ1,其中Θi={pi},且满足p0>…>pi>…>p1(i=2,3,…,m),则检验问题(2)式即可以划分为如下m对假设检验问题[19]:
(7)
由于(3)式中的似然函数比未能利用装备的先验信息,在充分考虑已有先验信息的基础上,需要给出包含先验信息的Bayes因子计算方法。
2.2 Bayes因子计算
考虑有现场试验数据序贯序列如1.3节所述的X={X1,…,Xi,…,Xn},由2.1节可得到m个SPRT方案,以(7)式中第j(j=1,2,…,m)对假设检验问题H0j和H1j为例,则Bayes因子Λj(X)可表示为
(8)
式中:PH0j和PH1j分别表示假设H0j和H1j成立的先验概率,且满足PH0j+PH1j=1,并有
(9)
其中:当j=1时,k1=0,k2=2;当j=2,3,…,m-1时,k1=j,k2=j+1;当j=m时,k1=m,k2=1.
设Lj和Uj为Bayes因子Λj(X)判决阈值的下界和上界,满足[16]:
(10)
式中:απ0j和βπ1j分别为考虑先验分布式的承制方和使用方风险,满足:
(11)
αj和βj分别表示(7)式中第j组假设检验问题的承制方和使用方风险值,由原假设检验问题(2)式给出的α和β决定。
为了得到序贯网图,做出如下推导:
1)接受H0j时,有Λj(X)≥Uj,两边取对数即可得到一条边界线lj:c=sjn+hj,边界线lj之下即为接受H0j的区域,斜率sj和截距hj分别为
(12)
(13)
2)接受H1j时,有Λj(X)≤Lj,两边取对数即可得到一条与lj平行的边界线l′j:c=sjn+h′j,边界线l′j之上即为接受H1j的区域,截距h′j为
(14)
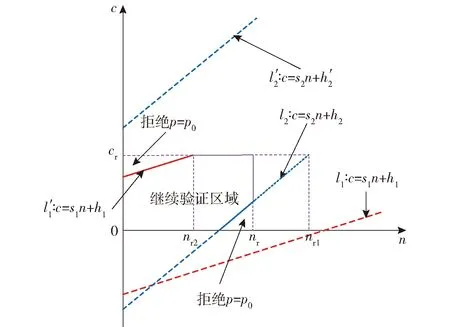
3)当Lj≤Λj(X)≤Uj时,即位于两条边界线lj和l′j之间的区域,为继续验证区域,不作出判决,需要开展下一次验证试验。
2.3 先验概率的运用
利用BSST进行统计分析时,先验信息来源主要为历史信息、仿真数据、专家经验信息以及各子系统信息等,根据数据类型进行划分,以上多源先验信息可划分为点估计形式、置信区间估计形式以及成败型数据形式,并通过对应的先验分布参数求解方法进行求解[20],然后融合得到FDR/FIR的先验分布为π(p),则先验概率PH0j和PH1j分别表示为对假设H0j和H1j的支持程度,有
(15)
通过(15)式即可求取第2.2节中(8)式~(14)式,由m对假设检验问题即可以得到m组平行线,根据m组平行线的相对位置关系即可确定基于BSST-SMT的验证试验判决边界。
确定PH0j和PH1j后,为了进一步得到απ0j和βπ1j,根据(11)式知需要考虑(7)式中第j组假设检验问题的αj和βj如何确定。考虑插入点后各组假设检验问题的继续试验区宽度不变的原则,即
h′j-hj≡C(常数).
(16)
(13)式和(14)式代入(16)式中便可以得到:
(17)
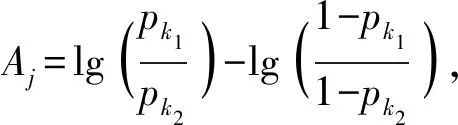
(18)
另外仍需再找一个αj和βj的关系才能最终确定(11)式,为了兼顾先验概率以及承制方和使用方风险,考虑先验分布下的风险比απ0j/βπ1j和双方风险比α/β相当的原则,即满足:
(19)
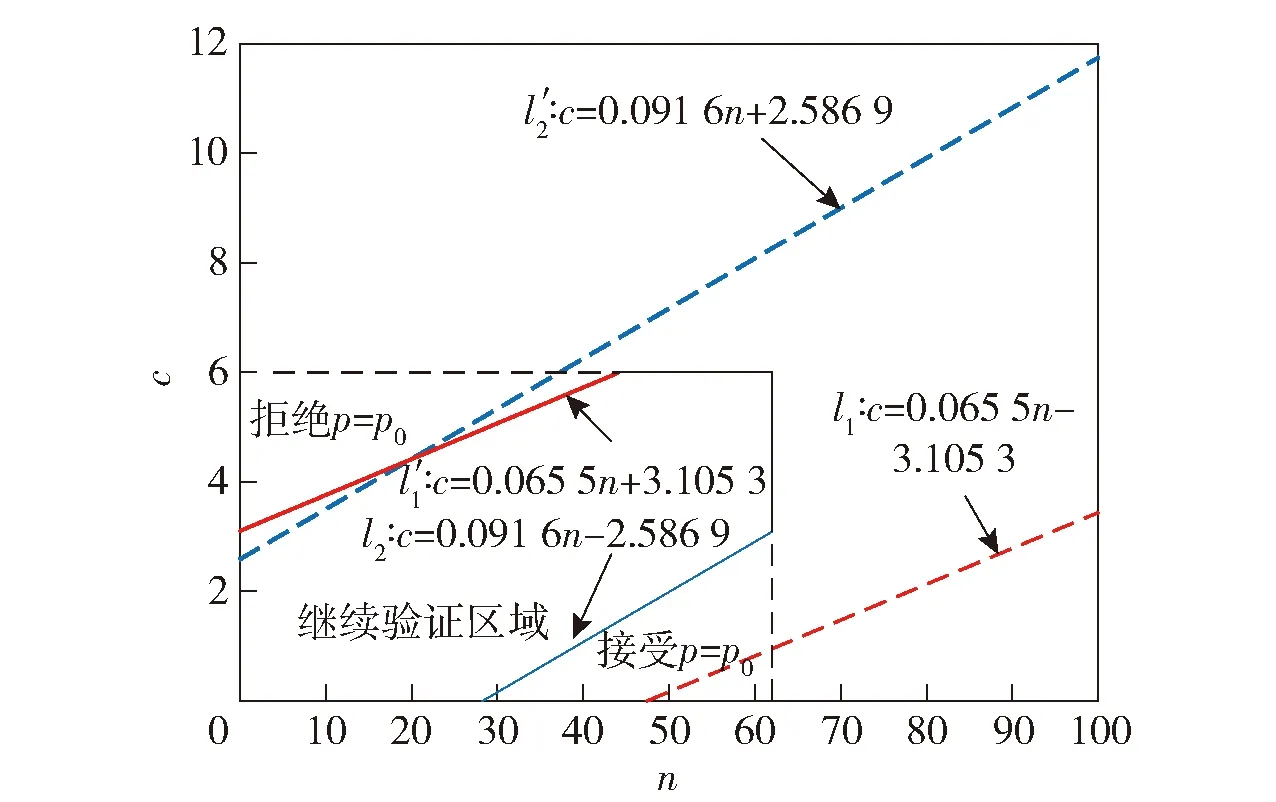
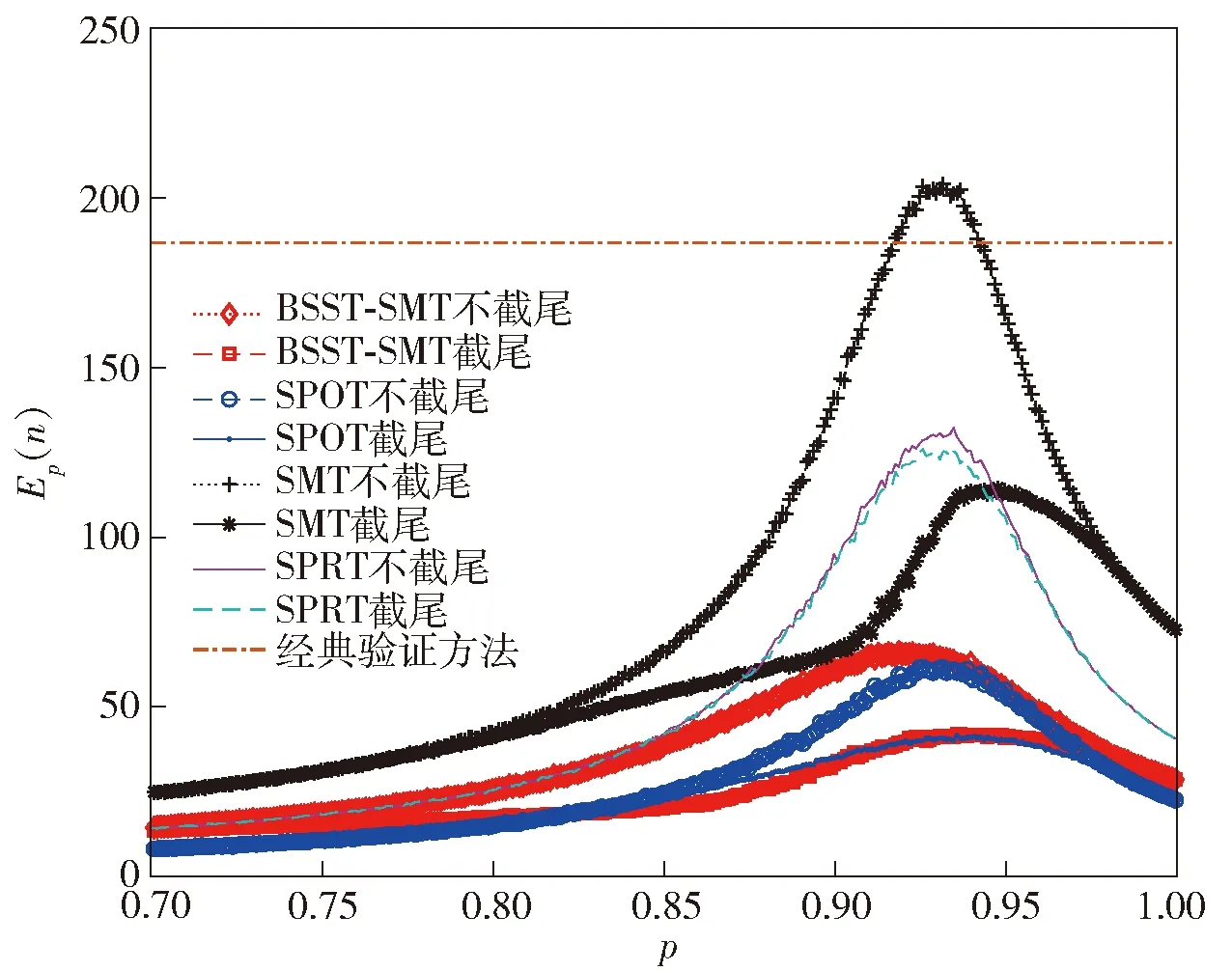
由于Bj还可以表示为Bj=Lj/Uj,而0 (20) 由于继续试验区宽度不变,根据p0、p1、α和β可以确定常数C为 (21) 据此即建立起αj、βj与插入点pi以及先验概率PH0j和PH1j的关系。 2.4.1 插入点数量的选取原则 设根据指标参数空间划分,另有一对假设检验问题如下所示: (22) 则可以得到如下定理。 定理1由检验问题(7)式和检验问题(22)式所确定的验证试验判决边界相同。 证明对于检验问题(7)式,可以确定拒绝p0的边界问题可以由第1对假设检验H01及H11所确定的一组平行线的上线(根据与c轴截距确定一组平行线的上线和下线)决定,同时可以确定拒绝p1的边界问题可以由第m对假设检验H0m及H1m所确定的一组平行线的下线决定,故可以判定验证试验判决边界的确定与(7)式中其余m-2对假设检验方案无关,即与检验问题(22)式所确定验证判决边界等同,即证。 定理1反映出插入m-1个点和插入2个点具备同样的判决边界。不同的是插入点数量的选择,决定了BSST-SMT方法所确定的最大样本量不同,由于仍需对截尾策略进行考虑,而增加插入点会增加计算复杂度,故本文考虑(22)式中p2=pm时的情况,即实施BSST-SMT方法时实际插入点为1个。 2.4.2 插入点位置的选取策略 基于插入点数量的选取原则,对问题进行一般化考虑,选取FDR/FIR指标插入点p2(p1 (23) 由(23)式可确定两组平行线l1‖l′1以及l2‖l′2,如图1所示。图1中n0是l′1和l2的交点横坐标,即表示BSST-SMT方法所确定的样本量上界,满足: (24) 图1 序贯网图检验Fig.1 Sequential mesh test 对插入点的选取策略即保证选取合适的插入点p2,使得n0能达到最小值。这正是因为对于BSST-SMT方法平均样本量和最大样本量均是需要考虑的因素,在平均样本量小的情况下,保证最大样本量也较小。 根据上述分析,直线l′1为检验问题(23)式中拒绝假设p=p0的判决边界,直线l2为检验问题(23)式中拒绝假设p=p1的判决边界,故取直线l′1和l2作为原始假设检验问题(2)式的判断边界,则通过图1可以确定BSST-SMT方法的判决区域为:1)l′1以上区域为拒绝p=p0的判断区域(即接受p=p1的判断区域);2)l2以下区域为拒绝p=p1的区域(即接受p=p0的判断区域);3)直线l′1和l2之间的区域即为继续验证区域。 由于要对验证试验风险进行控制约束,根据最大样本量n0或最大样本量n0下的最大允许检测/隔离失败数c0是否满足预期试验截尾数nE或cE,需要对截尾样本量nt(nt 2.5.1 考虑截尾样本量 1)通过BSST-SMT方法得到的最大样本量n0满足预期试验截尾数nE要求,即n0≤nE,则序贯截尾策略即选用n0,则n≥0,c≥0,直线l′1和直线l2所围成的区域即为继续验证试验区,如图1所示。 2)最大样本量n0过大,即n0>nE,需要考虑截尾样本量nt以及对应的最大允许接受值ct(ct1≤ct≤ct2),其中ct2=s2nt+h2,ct1=s1nt+h′1,且(nt,ct)的确定原则是在满足承制方和使用方风险的前提下使得nt和ct最小,则0≤n≤nt,0≤c≤ct,直线l′1和直线l2所围成的区域表示截尾限制条件下的继续验证区域,如图2所示。 图2 考虑截尾样本量nt的序贯网图检验Fig.2 Sequential mesh test in considering the censored sample size nt 2.5.2 考虑最大允许截尾检测/隔离失败数 1)通过BSST-SMT方法得到的最大允许检测失败数c0满足预期试验截尾数cE要求,即c0≤cE,则序贯截尾策略即选用c0,则n≥0,c≥0,直线l′1和直线l2所围成的区域即为继续验证试验区,即不考虑截尾策略的序贯网图,仍如图1所示。 2)最大允许检测/隔离失败数c0过大,即c0>cE,需要考虑最大允许截尾检测/隔离失败数cr以及对应的样本量nr(nr2≤nr≤nr1),其中cr2=s2nr2+h2,cr1=s1nr1+h′1,且(nr,cr)的确定原则是在满足承制方和使用方风险的前提下使得nr和cr最小,则0≤n≤nr,0≤c≤cr,直线l′1和直线l2所围成的区域表示截尾限制条件下的继续验证区域,如图3所示。 图3 考虑最大允许检测/隔离失败数cr的序贯网图检验Fig.3 Sequential mesh test in considering the maximum allowable number of detection/isolation failures cr 对于工程实际而言,侧重于考虑截尾样本量的截尾方案,即偏向于通过观测截尾样本量nt值,来确定最大允许截尾检测/隔离失败数ct. 故本文采取如图2所示的截尾方案,实际的承制方风险即装备测试性水平p=p0时,装备未能通过验证的所有拒收情形的概率之和,同理实际的使用方风险即为p=p1时,装备通过验证的所有接受情形的概率值之和,具体可表示为 (25) 式中:Nr表示确定序贯网图后所有拒收点的数量;Na表示所有接收点的数量;ci、cj表示到达当前拒收点以及接受点的检测/隔离失败数;ni、nj表示到达当前拒收点以及接受点的总样本量;Si、Sj则表示到达当前拒收点以及接受点的所有可能情况。将(25)式用序贯网图相关参数表述即为 (26) 式中:αr表示实际承制方风险;βr表示实际使用方风险;Pp0(·)表示在假设p=p0成立条件下的概率;Pp1(·)表示在假设p=p1成立条件下的概率。 通过第2节的分析,基于BSST-SMT的测试性验证试验方案由4个指标参数(p0,p1,α,β)和9个设计参数(π(p),s1,h1,h′1,s2,h2,h′2,nt,ct)所确定。其中4个指标参数由承制方、使用方具体确定,9个设计参数可以分为3类,其中π(p)表示先验分布,(s1,h1,h′1,s2,h2,h′2)能清楚直观地反映序贯网图的斜率和截距,(nt,ct)表示截尾样本量和最大允许检测/隔离失败数,通过设计参数之间的联系以及约束限制,即可完成方案设计。具体方案设计实施流程如下: 步骤1确定先验分布π(p). 根据装备各层级、各阶段或者历史型号试验信息等,根据不同先验来源采取不同的信息处理方式,可参见文献[20],本文不作重点讨论。 步骤2确定插入点p2. 插入点p2的确定可以由如下优化问题进行确定: (27) 式中:s1、s2、h2和h1可通过(10)式~(15)式进行确定,该优化问题是插入点p2和最大样本量n0间的优化问题,通过Matlab编程即可实现。 步骤3当通过优化问题(27)式确定插入点p2后,即可确定设计参数s1、h1、h′1、s2、h2和h′2. 步骤4确定截尾样本量nt. 截尾样本量nt可以由另外一组优化问题进行确定: (28) 式中:αr和βr可通过(26)式确定;ct1和ct2可通过步骤2确定的直线l1和直线l′2确定。 步骤5确定最大允许截尾检测/隔离失败数ct. 在确定截尾样本量nt之后,ct的确定仍可通过优化问题决定: (29) 对于优化问题(28)式和(29)式采取搜索算法,搜索次数受所确定的截尾样本量和最大允许检测/隔离失败数约束,可通过编程实现。当找到满足优化问题(28)式和(29)式的nt和ct,便可绘制如图2所示的截尾序贯网图,即完成了验证方案的设计。 由基于BSST-SMT的测试性验证试验方案设计方法可知,对于装备FDR/FIR验证试验均能试用,本文以某装备飞行控制系统FDR的验证为例,根据承制方和使用方要求,有FDR约束指标参数为 (p0,p1,α,β)=(0.95,0.90,0.1,0.1). (30) 1)对于BSST-SMT方法,先验信息来源于装备的各层级、各阶段信息以及历史型号试验信息等。现仅考虑历史型号试验信息,原来装备测试性验证试验过程中,注入了80次故障,74次故障得到正确检测,6次故障未能成功检测。在数据处理上采用Hart运用的经验Bayes方法,即认为历史装备的试验等价于对当前装备进行了60%次数的试验[21]。因此,先验分布超参数为(74×0.6,6×0.6)=(44.4,3.6),故先验分布满足: (31) 2)根据步骤2中的优化问题(27)式求解插入点p2. 求解得到插入点p2=0.916 4,对应的最大样本量n0=⎣217.997 2」=217(符号⎣」表示向下取整)。同时能得到插入点p2和最大样本量n0的关系变化曲线如图4所示,更直观反映出优化问题的最优解确实为图中标记的点。 3)根据步骤2可以得到设计参数s1=0.065 5,s2=0.091 6,h′1=3.105 3,h1=-3.105 3,h′2=2.586 9,h2=-2.586 9. 4)采用搜索的方法,让nt从1开始搜索,同时对ct1≤c≤ct2进行搜索,直到找到优化问题(28)式的解,搜索得到截尾样本量nt=62. 5)在确定截尾样本量nt=62后,对ct1≤ct≤ct2重新进行搜索,以找到优化问题(29)式的最优解。搜索得到当前截尾样本量下对应的最大允许检测失败数ct=6,同时有αr=0.056 0,βr=0.082 9. 据此可以绘制序贯网图如图5所示。 图5 飞行控制系统序贯网图检验Fig.5 Sequential mesh test of flight control system 1)经典验证方法。根据(1)式可以得到经典验证方案为(187,13),实际的承制方风险αr=0.087 4,实际的使用方风险为βr=0.098 1. 2)常规SPRT方法[22]。验证开展前无法确定其样本量上界,根据(3)式~(6)式可以得到其平均样本量Ep(n)最大值为132. 同时国际标准IEC1123给出了截尾SPRT方案为(286,20),采用Monte Carlo仿真的方法进一步确定其平均样本量最大值为126. 3)传统SMT方法[23]。验证前可以确定插入点p2=0.927 6,然后得到最大样本量n0=472,以及该样本量下的最大允许检测失败数c0=34,试验平均样本量最大值为204. 在此基础上采取截尾策略,得到的截尾SMT方案为(143,12),截尾策略条件下实际的双方风险为αr=0.084 3,βr=0.091 8,最大平均样本量为114. 4)SPOT方法[18]。SPOT方法与SPRT方法一样,验证开展前无法确定样本量上界,采用Monte Carlo方法仿真可以得到其最大平均样本量为64. 在此基础上考虑截尾策略,通过本文给出的先验分布,采用α=0.08+0.02、β=0.08+0.02的风险拆分方式,得到截尾样本量nt=63,以及截尾判据阈值0.722 1,该截尾方案下的最大平均样本量为42,实际的双方风险值为αr=0.08+0.001 4=0.081 4,βr=0.08+0.003 3=0.083 3. 5)本文提出的BSST-SMT方法。本文确定的最大样本量n0=214,对应的最大允许检测失败数c0=17,采用Monte Carlo方法得到平均样本量为66. 在此基础上采取本文给出的截尾策略,得到截尾基于BSST-SMT的测试性验证试验方案为(62,6),截尾策略条件下实际的双方风险值为αr=0.056 0,βr=0.082 9,平均样本量为42. 以上所提平均样本量的计算,均采用Monte Carlo仿真方法,设置仿真次数为1 000,同时将FDR的取值区间(0,1]分为1 000个离散值进行仿真,得到图6所示的平均抽样次数随FDR变化关系曲线,根据曲线可以确定平均样本量取最大值时的p值,以及根据不同的p值确定其平均样本量的值,如本文提出的BSST-SMT截尾方法中,p=p0时平均样本量Ep0(n)=41,p=p1时平均样本量Ep1(n)=33,在SPOT截尾方法中Ep0(n)=41. 从图6中可以直观地反映出,本文所提方法在满足指标约束条件的基础上,平均样本量和截尾样本量均明显优于经典验证方法、SPRT截尾方法以及SMT截尾方法,和SPOT截尾方法相当,但实际的承制方和使用方风险均优于以上方法。由此可见,该方法确定的测试性验证截尾样本量以及平均样本量均优于其他方法,同时能有效降低双方风险值,证明了方法的有效性。 图6 不同验证方法的平均样本量曲线对比Fig.6 Comparison of average sample size curves for different testablility verification methods 本文基于BSST-SMT的测试性验证试验方案设计方法结合传统SMT方法和BSST优点,利用待检测装备系统的先验信息,分别从检验点、Bayes因子、先验概率、截尾策略等方面对验证方案进行设计,实现了样本量的确定,其优点是: 1)由于在测试性指标约束下考虑了装备系统的先验分布,使得确定的样本量更为客观准确。 2)解决了常规SPRT方法和SPOT方法不考虑截尾时最大样本量无法控制的问题,BSST-SMT方法能在验证试验开展前能确定最大样本量,使得对验证试验开展有比较客观的认识。 3)解决了传统SMT方法不能利用先验信息的问题,结合BSST处理先验信息,将先验信息用于SMT方法中,达到降低最大样本量、平均样本量以及双方风险的目的。 4)本文基于BSST-SMT的测试性验证试验方案设计方法较之经典验证方法、常规SPRT方法、传统SMT方法以及SPOT方法在最大样本量、平均样本量以及双方风险值等方面均有有效改进,能更好的指导高精度武器系统的验证试验的开展。 与此同时,除了在文中进行讨论的研究点外,仍然有一些问题需要深入研究:保证试验的充分性需要足够的样本量,而确保验证试验代价最小需要保证样本量足够小,所以样本量的确定应在二者之间权衡,对样本量确定方法的选择是即考虑充分性和代价之间折中的过程,所以如何合理的选取截尾策略需要进一步研究。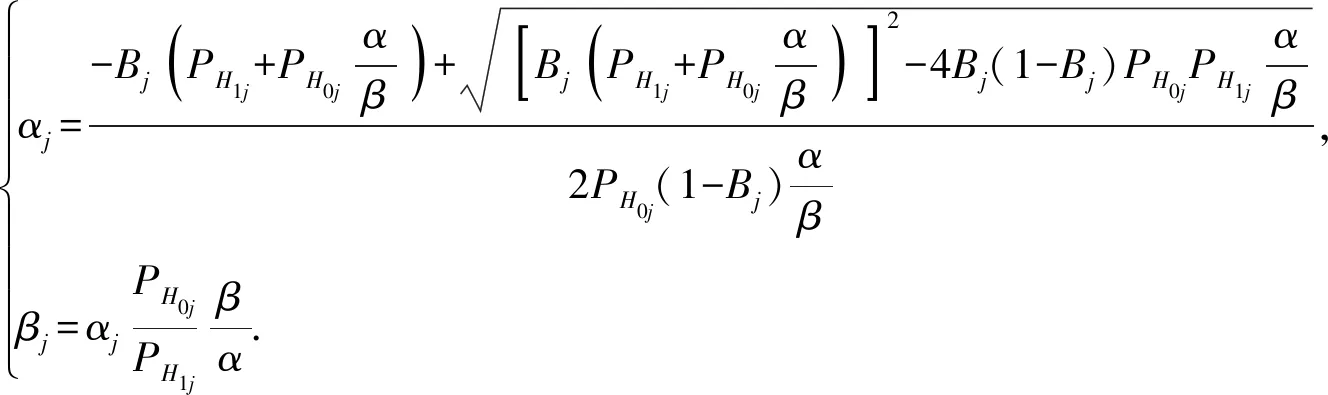
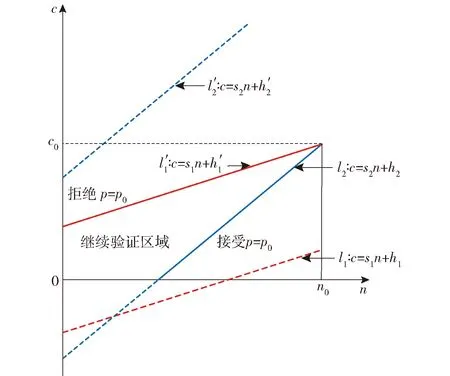
2.4 插入点选取策略
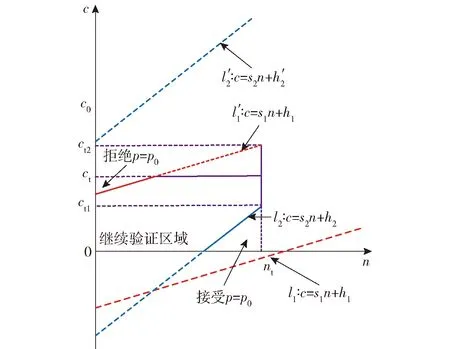
2.5 截尾策略
2.6 双方风险计算
3 验证方案设计流程
4 实例分析
4.1 基于BSST-SMT的验证方案设计
4.2 对比分析
5 结论
