履带式果园作业车平地直行和转向仿真研究及试验
2019-12-22党革荣薛杨春王耀凤
崔 恩,党革荣,程 健,陈 军,薛杨春,王耀凤
(1.西北农林科技大学 机械与电子工程学院,陕西 杨凌 712100;2.西安市农机监理与推广总站,西安 710065)
0 引言
我国是世界上最大的水果生产国和消费国,随着水果种植业的不断发展,果园机械的开发需求正在不断的提升,未来我国果园采摘机械的发展趋势主要体现为多功能化、操作简便、可靠性高、通用性好及自动化和智能化等特点[1]。履带式作业车辆作为采摘机械的一种类型,具有良好的通过性能,在农业机械、建筑行业及军事领域发挥着十分重要的作用[2]。本文以研制的履带式果园作业车为研究对象(见图1),采用多体动力学仿真软件RecurDyn对果园作业车进行动力学建模,通过仿真试验来研究履带式果园作业车在不同工况下的动力学性能[3-4],并通过实地试验对仿真结果进行简单验证,旨在为履带式果园作业车进一步的改进设计提供理论参考依据。
1 整机仿真模型的建立
运用多体动力学仿真分析软件RecurDyn自带的履带车辆子系统Track(LM)建立履带式果园作业车三维多体动力学模型如图2所示,设置整机各部分质量如表1所示。整机模型包括履带底盘、车架、升降平台及油箱等部件,履带底盘由驱动轮、导向轮、支重轮、托带轮、履带板等各种履带行驶系统组件组成[5]。按照简化原则,在不影响仿真结果的情况下,对一些零部件(如螺栓、螺母等)做出适当的简化来提高仿真速度。

图1 履带式果园作业车Fig.1 The tracked of orchard vehicle

图2 履带式作业车仿真模型Fig.2 The tracked of orchard vehicle simulation model

表1 履带式作业车各器部件质量Table 1 Mass of each for the tracked of orchard vehicle component kg
为了使仿真结果更加接近真实情况,需要在两构件之间添加约束,在相对运动的部件间增加摩擦因数。机构内部的摩擦阻力系数通常取经验值,本文在RecurDyn中取各个旋转副的摩擦因数为0.07。
履带式果园作业车采用液压马达驱动作为动力输出装置,液压马达输出动力使驱动轮转动,从而促使履带带动整机行驶。通过预设的驱动函数分别作用于左、右两侧驱动轮上,进而通过液压马达输出的动力,实现作业车的行进运动。
本文在RecurDyn软件中使用的是STEP函数对整机施加驱动。该函数采用三次多项式逼近阶跃函数,表达式为
(1)
式中x0—阶跃起点的自变量值;
x1—阶跃终点的自变量值;
h0—阶跃起点的函数值;
h1—阶跃终点的函数值。
2 地面模型与地面力学关系的建立
履带式行走车辆在进行仿真建模和分析时要建立与实际路况相接近的相应正确力学模型,因此在对履带式果园作业车进行动力学仿真研究的过程中将作业车底盘部分与行进地面间的相互关系作为首要考虑因素。
在研究行进地面的力学特性时,首先需要将土壤的变形用土壤的承压特性和剪切特性表示[6]。在坚实地面路况上,通过履带车辆与地面之间相互作用产生的接触力来反映履带与行进地面之间的压力,在RecurDyn软件中接触碰撞力F计算公式为
(2)
式中q-q0—地面沉陷量;

相关理论和试验证明,指数n取2~3时计算所取得的仿真效果速度最佳,同时土壤阻尼c和刚度系数k对仿真结果也有较大影响。基于美国专家贝克提出的压力—沉陷关系式,确定履带对软地面的正压力计算公式为
(3)
式中Kc—土壤内聚力变形模量;
b—履带板宽度;
Kφ—土壤内摩擦变形模量;
Z—土壤沉陷量。
在多体动力学仿真软件RecurDyn中,履带在接触的地面上产生剪切作用,剪切力-位移关系式为[7]
(4)
式中c—地面压力为0时的最大剪切应力;
p—地面压力;
φ—土壤内摩擦角;
j—剪切位移;
k—水平剪切变形模量。
本文研究的履带式果园作业车,主要在北方的砂壤土果园下进行作业。在RecurDyn软件中进行动力学性能分析时,将砂壤土设为地面模型土壤,参数如表2所示。
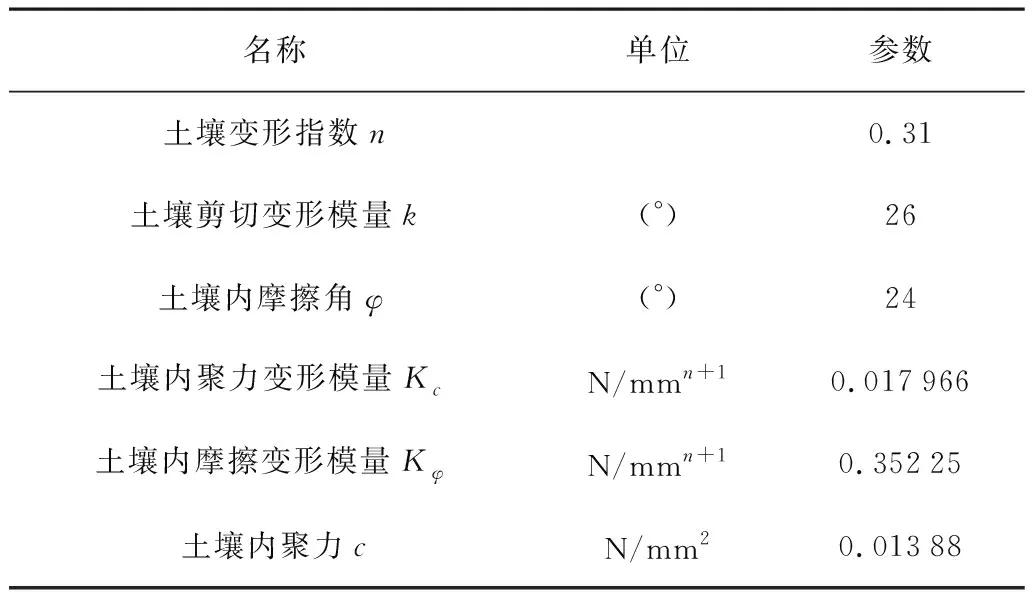
表2 砂壤土基本参数Table 2 Parameter of sandy loam
3 履带式果园作业车仿真分析
进行运动学和动力学分析之前,在RecurDyn软件中首先进行样机模型的预分析和静平衡阶段探究,确保分析结果的有效性和准确性[7]。通过预分析得出履带式果园作业车的仿真模型中共包括29个刚体和2个履带装配体,整机自由度为484个,没有冗余约束。所谓静平衡阶段分析,是指整机模型在自身重力的作用下自然落到水平地面模型上,并缓慢进入静平衡状态的过程。
3.1 平地直行工况分析
通过分析履带车辆的接地压力、履带行走过程的总阻力、沉陷深度等指标来验证履带式作业车辆直线平地行驶性能,包括能否在预设的平地上完成直线加速、匀速、减速及停止的运动。在此仿真模拟过程后,对实验中仿真的数据进行提取和研究分析。选定履带底盘装置中第1块履带板记为履带板A,通过履带板A的纵向位移变化及履带板与地面的间的应力力变化来反映整机模型的沉陷深度和接地应力,如图 3和图4 所示。
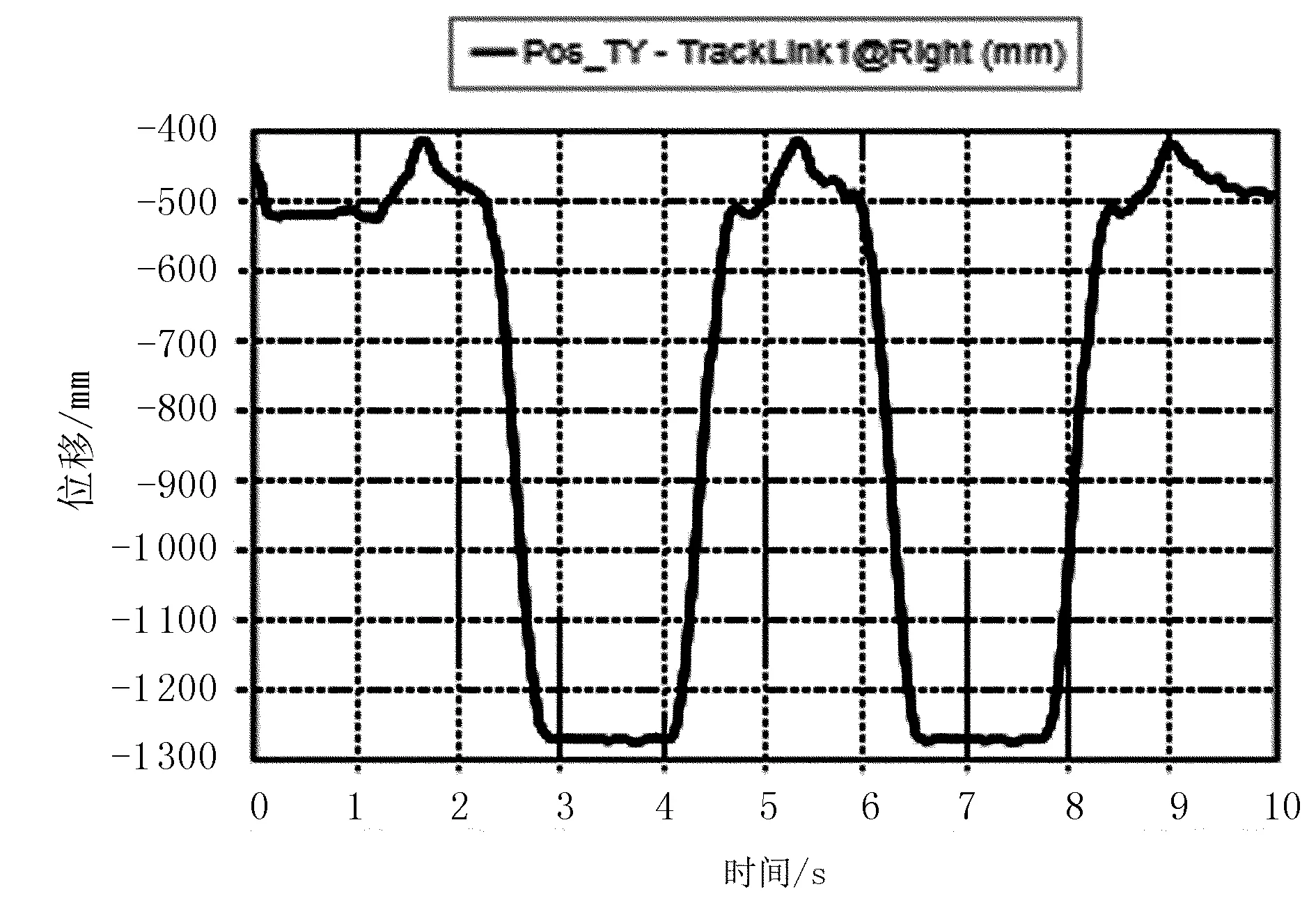
图3 履带板A的纵向位移Fig.3 Longitudinal displacement of tack linkA

图4 履带板A与地面的应力变化Fig.4 Pressure changes of the tack linkA to ground
由图3可以看出:在约1.6s时,曲线上升并达到运动过程的最高点,表明履带板A已运动至托带轮处;在1.6~3s时间段内,曲线开始陡然下降,表明履带板A从导向轮上边沿逐步开始下降;在3~4s时间段内,曲线平缓并处于最低峰,表明履带板A到达最低点,与地面接触,随后履带板A又沿着驱动轮上升,进入下一圈循环。由图4可以看出:曲线有几处明显的波峰,首先第1处波峰的产生是由于履带板A离开导向轮,被挤压陷入土壤中,土壤对其形成的应力;最后一处波峰是驱动轮对其施加的力,中间几处波峰是由于履带板A受到支重轮的压力造成的。
由匀速行驶时驱动轮上的驱动力大小来代表整车行走时行走装置的总阻力大小[8],驱动轮上的驱动力矩如图5所示。其中,在1.6s前为整车启动的过程,这个过程需要加速,驱动力矩先逐渐增大后减小,最大值达到-2 044 277N·mm;由于启动时要克服惯性阻力,因此驱动力矩较大,等作业车运动趋于平稳,驱动力矩又减小到某一值。在1.6s~9s时为果园作业车匀速行驶过程,需要的驱动力矩则较小,由此可以看出,履带式果园作业车在加速启动阶段需要的动力远大于匀速行驶时;当速度达到3km/h、匀速行驶7.5s过程中,整机受力均匀,运行平稳,驱动力矩曲线有规律的上下波动,引起这种情况的原因是链传动的多边形效应;从第9s开始,整机减速制动阶段,驱动力矩先增大后减小,最大值达到1 415 033N·mm。由此可以看出,整机在加速启动时动力需求相对较大。

图5 驱动力矩Fig.5 Driving torque
3.2 平地转向工况分析
针对履带作业车在田间作业时的平地转向工况进行分析,所使用的主要转向方式为差速转向和抱死转向,即一侧履带的驱动力增加或不变,而另一侧履带驱动力减小或制动,由此会产生一个转向力矩。转向的灵活性和操控性是履带车辆机动能力的重要指标之一,研究其性能对其合理的使用具有重要意义[9]。对由平地环境转向工况环境进行仿真前,应该选择一个符合实际、满足条件并且相对合理的行驶速度。图6为不同车速下(1.2km/h和3.0km/h)转向整机垂向位置的变化曲线,横坐标代表时间,纵坐标代表整机质心位置。由图6可以看出:行驶速度为1.2km/h时,质心的波动幅度较小。因此,在接下来的转向工况仿真中采用速度1.2km/h进行仿真试验。
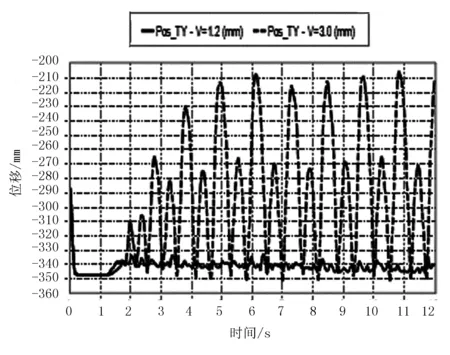
图6 不同车速下作业车的纵向位移Fig.6 Longitudinal displacement of overall unit at different velocity
转向性能是表征车辆改变其运动方向的一种能力,主要通过最小转向半径、转向角速度及转向角加速度等指标评价。其中,转向角速度是评价履带车转向性能的重要指标[10],如图7所示。由图7可知:履带式果园作业车在差速转向时的转向角速度相对较小,波动变化小,均值约为0.15rad/s,说明履带式作业车差速转向的稳定性相对较好;而抱死转向的转向角速度较大,且波动也较大,均值约为0.36rad/s,说明履带式作业车抱死转向方式的稳定性相对较差。由此表明,差速转向相较于抱死转向更趋于平稳,但完成相同的转向要求时差速转向方式需要更大的转向半径,影响了作业车整机的机动性。

图7 作业车辆转向变化时角速度Fig.7 Steering angular velocity of overall
转向角加速度是车辆转向时侧翻与否的重要指标,如图8所示。转向角加速度越大,则产生的离心力越大,车辆就越容易发生侧翻。由图8可知:车辆采用差速转向方式时其转向的角加速度相对较小,均值约为0.007rad/s2,而抱死转向时其转向角加速度相对较大,均值为0.068 rad/s2;差速转向与抱死转向角加速度曲线变化规律基本一致,但相较于抱死转向方式,差速转向方式的角加速度幅值波动较小,较易趋于稳定[11]。由此表明,作业车辆差速转向方式比抱死转向方式稳定性好;但不论哪种转向方式,作业车内外侧履带会同时受到阻力,都是外侧履带克服的阻力较大、内侧履带克服的阻力较小。
根据仿真结果,履带车样机采用差速转向的方式。

图8 整机转向角加速度Fig.8 Steering angle acceleration of overall unit
4 履带式果园作业车直行和转向试验
4.1 平地直线行驶试验
采用履带车中心安装滴水器滴水,沿水线每隔20cm摆放一个小模块办法来实现轨迹划线,水线及小模块宽度均小于10mm,测量误差较小可以忽略。
选取坡度为0°的实验场地,使作业车处于正常工作状态,在现有路面条件下,以低挡、中挡、高挡直线行驶。由直线行驶轨迹(见图9)可知:基于预设的驱动函数和控制系统控制下,车辆在行驶过程中轨迹偏差较小,最大偏差为0.08m,方差为0.000 78,说明履带式作业车在控制系统控制下直线行驶度比较高。
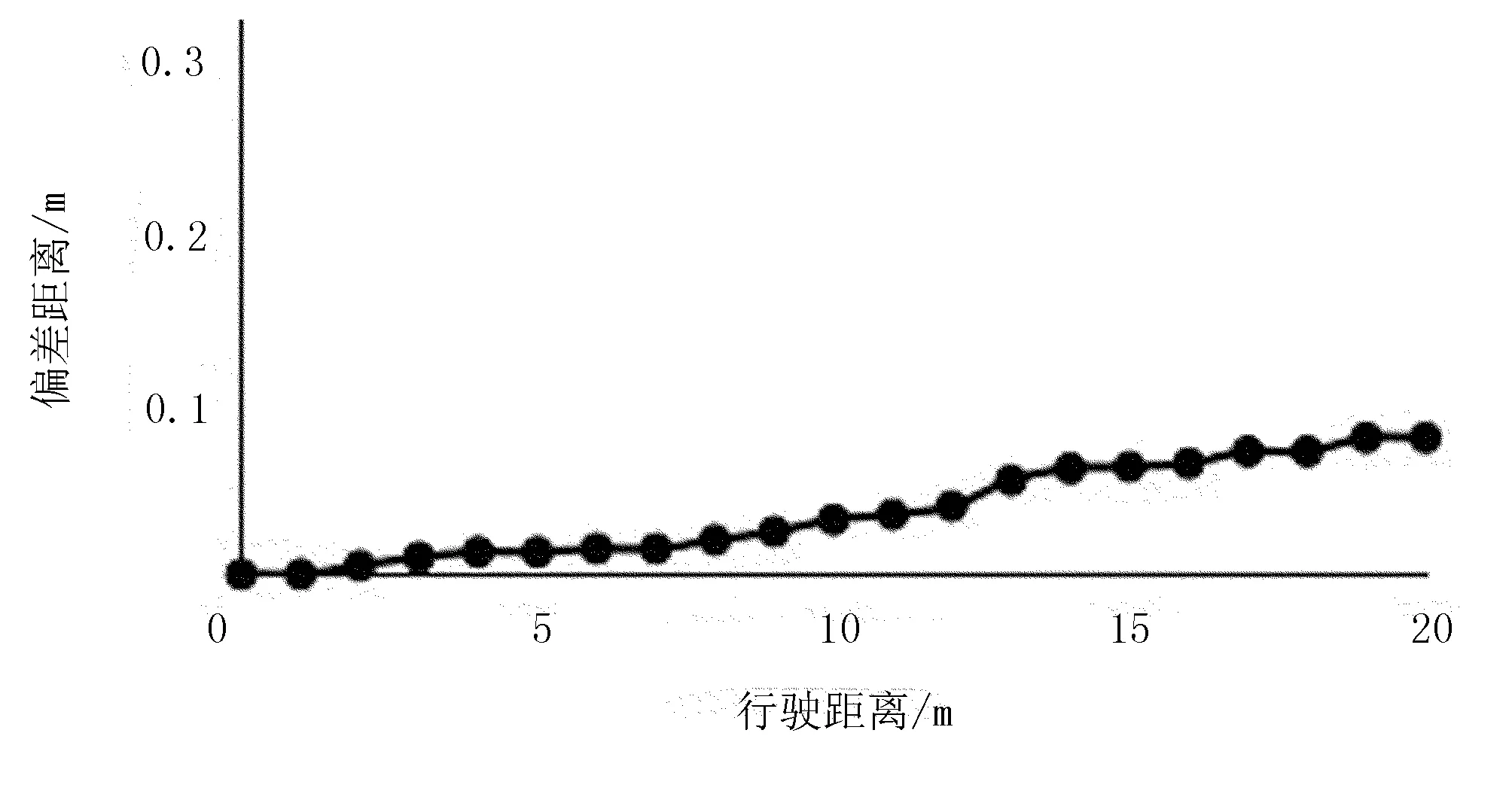
图9 整机直线行驶轨迹Fig.9 Track line of line running
4.2 平地转向行驶试验
根据履带车工作需求试验了180°转向,在排除人为遥控操作情况下,试验自设的转向控制系统的转向情况,如图10所示。由图10可以得出,履带车自设转向控制系统能够实现180°的转向。
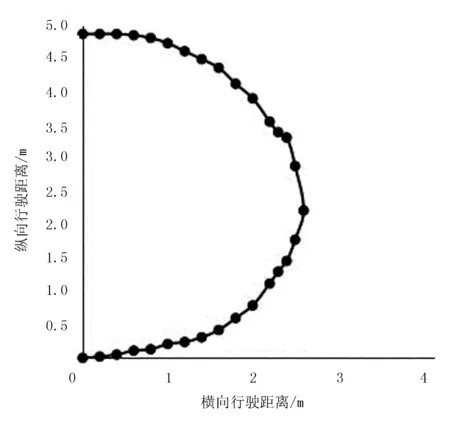
图10 180°转向行驶轨迹Fig.10 Transplanter track of marching 180°
5 结论
1)在平地直行工况下,仿真得出接地压力、沉陷深度及驱动力矩曲线,分析可知整机在获得驱动力时性能良好。
2)通过平地转向工况下对其转向性能进行动力学仿真实验,分析转向角速度与转向角加速度曲线,结果表明:行驶速度越高,离心力越大,转向时其稳定性就越差;抱死转向相比差速转向,其转向阻力大,稳定性低,但转向半径较小,转向较快。
3)履带式果园作业车的平地直行和转向试验与仿真结果基本一致,从而验证了整机模型的正确性,为履带式果园作业车进一步改进设计提供了理论参考依据。
