马铃薯仿生挖掘铲片及其减阻特性研究

2019-12-22李晓鹏潘群林陶金京

农机化研究 2019年6期

李晓鹏，廖敏，2，胡奔，潘群林，陶金京

(1.西华大学机械工程学院，成都 610039；2.流体与动力机械教育部重点实验室，成都 610039)

0 引言

随着农业产业结构调整和马铃薯主粮化战略的实施，马铃薯生产发展前景看好，种植面积稳中有增。马铃薯人工收获作业劳动量大，耗时费工，实现机械化收获是必然趋势。挖掘是马铃薯收获中最重要的环节，在含有马铃薯块茎、残根和石块的土壤中工作，阻力很大，这就要求挖掘铲具有较高的性能[1]。对马铃薯收获机挖掘铲触土部件进行仿生改形设计，进而提高其减阻性能，是一种新的研究途径。目前，国内对挖掘铲片的仿生设计和减阻性能已有一些相关的研究：邹翔翔等[2]分析得出倾角在25°～30°之间、铲齿为空心的仿生挖掘铲具有较好的质量、力学特性和寿命；石林榕等[3]设计的仿生挖掘铲片，利用LS-DYNA软件仿真得出仿生铲片较普通铲片阻力减小近61%；胡宗政等[4]设计的仿生挖掘铲模型利用LS-DYNA对铲片挖削土壤过程仿真，发现仿生挖掘铲片对土壤应力较集中且铲尖处应力最大；王玉晶等[5]运用离散元软件对新型仿生挖掘铲工作过程中所受的阻力及土壤破碎率进行了动态仿真，与普通挖掘铲相比较，仿生挖掘铲在X方向上的平均减阻率为10.41%，在Y方向上的平均减阻率为16.28%，土壤破碎率提高了2.67%。仿生挖掘铲的设计将仿生触土曲面与具有较好碎土性能的二阶平面铲设计原理相结合，对所得仿生信息进行处理，得到复合函数组成的仿生曲线，利用离散元软件EDEM进行挖掘过程仿真，对设计的复合函数仿生挖掘铲的挖掘过程进行仿真，与普通挖掘铲进行对比，研究其减阻和碎土性能。

1 马铃薯仿生挖掘铲片的设计

1.1 蝼蛄前爪第一趾仿生信息的获取

如图1(a)所示：蝼蛄，又名土狗子，触角短于体长，前足开掘式。我国已知有4种，即华北蝼蛄、东方蝼蛄、欧洲蝼蛄和台湾蝼蛄。其中，东方蝼蛄遍及全国，一般在长江以南东方蝼蛄较多，其主要生活于地下15～20cm土层。东方蝼蛄前足爪趾正向上形状似铲，其构形适于土中挖掘，侧向上形成具有一定弧度的曲面[6]。与其它具有挖掘能力的生物不同，蝼蛄主要依靠挖掘足在土壤中前进，中足和后足在挖掘时起到支撑身体的作用，蝼蛄前足的挖掘过程包括“切削土壤”和“扩张土壤”两个动作，其挖掘速度极快，每分钟可掘进相当于其体长5～7倍的距离[7]。本文主要研究其“切削土壤”这个动作，将其运用到马铃薯仿生掘铲的设计当中。蝼蛄前爪(即挖掘足)共有4趾，第1趾最大，第4趾最小。本文仅选取蝼蛄前爪第1趾作为仿生反求对象，进而获取轮廓曲线。

本实验选取蝼蛄前爪趾，去除与其减阻效果无关的跗爪大趾及羽状刺结构，只保留挖掘足特化的胫节部分(即主要触土部分)，将蝼蛄前足胫节爪趾第1趾置于精密三维显示系统(显微镜)下进行拍照，如图1(b)所示。获取垂直于切削土壤的法向截面的图像(即侧面轮廓图像)，如图1(c)所示。

图1 仿生图像信息采集Fig.1 Bionic image information acquisition

1.2 蝼蛄爪趾侧面轮廓线拟合

1.2.1 蝼蛄爪趾侧面轮廓线样条点获取

数字图像处理中，轮廓提取的算法较为成熟。首先，对图像进行灰度化处理和二值化处理，便于提取图像信息和凸显目标的轮廓；接下来，对二值图像的空洞区域进行填充，采用腐蚀运算来消除小的噪声点，删除小区域，采用膨胀运算将图像中的缝隙桥接起来。处理过程中多次用到腐蚀和膨胀运算，断开了狭窄的连接，消除了细毛刺，平滑了轮廓，能够较为准确地提取出蝼蛄前爪趾第1趾的轮廓线条。图像处理流程图如图2所示。

图2 图像处理流程图Fig.2 Flowchart of image processing

处理后轮廓图像如图3(a)所示。将处理后所得轮廓线条的图像以PNG图片格式导入到MatLab中，运用MatLab对内、外轮廓曲线的像素点进行坐标提取，提取的坐标以数据点的格式导出。

1.2.2 蝼蛄爪趾轮廓曲线的拟合

将两组轮廓图像的点数据(即提取所得像素点坐标)绘制在坐标系中，如图3(b)所示。

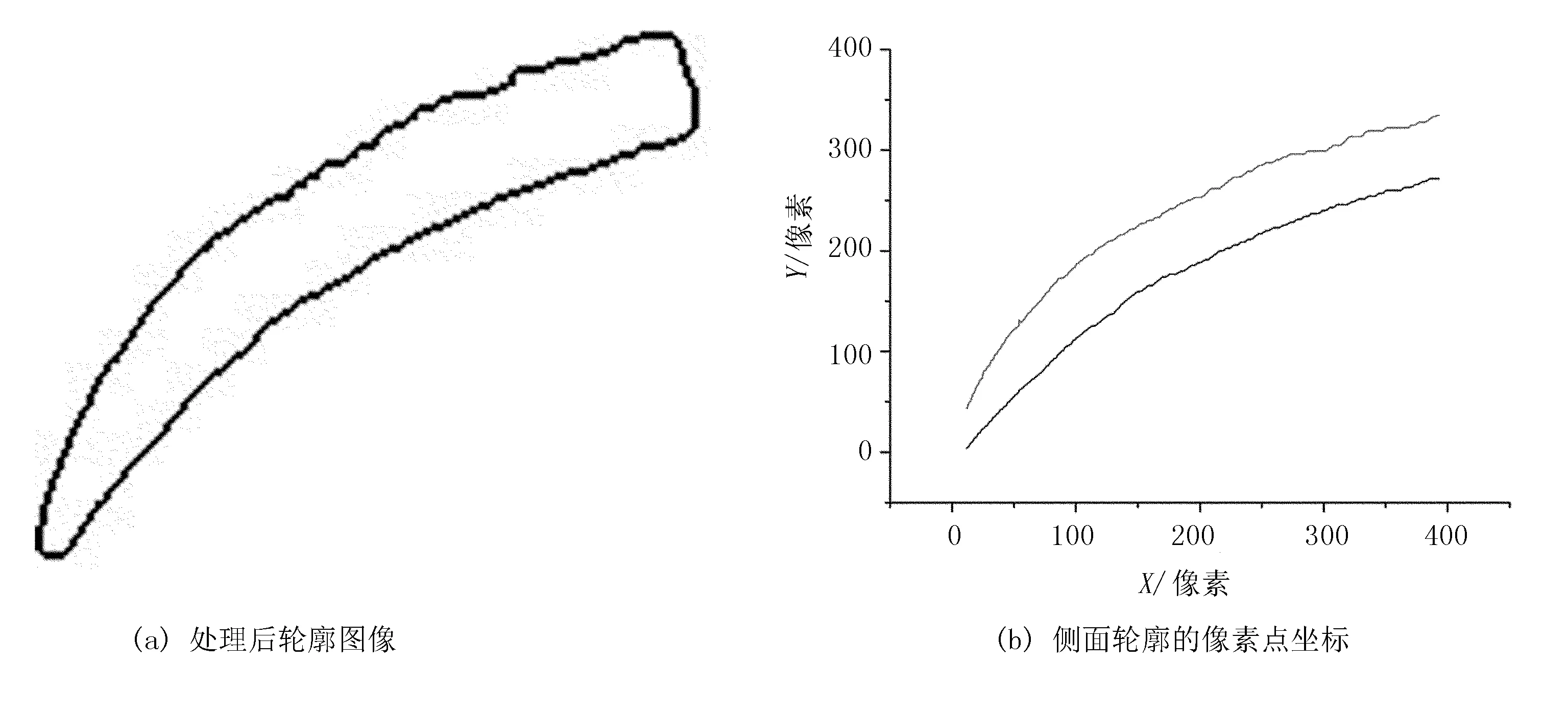
图3 轮廓图像处理Fig.3 Contour image processing

在MatLab中进行多项式拟合，分别得到蝼蛄爪趾的内、外侧轮廓曲线拟合后的函数表达式。内侧：y=ax6+bx5+cx4+dx3+ex2+fx+g，a=1.70732E-14 ，b=-4.71343E-12，c=-9.03933E-8，d=6.37403E-5，e=-1.7809015E-2，f=3.000146739，g=7.933154961，拟合度R2=0.9995；外侧：Y=AX6+BX5+CX4+DX3+EX2+FX+G，A=5.90732E-13 ，B=-8.29426E-10，C=4.4825E-7，D=-1.1418E-4，E=1.2007052E-2，F=0.615150932，G=16.57794569，拟合度R2=0.9997。

1.3 马铃薯挖掘铲片仿生设计

为了对比普通挖掘铲片和仿生挖掘铲片在挖掘土壤过程中所受阻力差异，应用CREO 2.0软件对两种挖掘铲铲片进行建模。仿生挖掘铲片上下铲面均为仿生曲面，铲尖两端仿蝼蛄趾尖端部进行倒角，如图4(a)所示。普通挖掘铲上下铲面均为平面，如图4(b)所示。为了保证铲片和马铃薯收获机挖掘装置连接后在工作过程中不会出现松动，铲片末端均设有两个铆钉沉头孔。

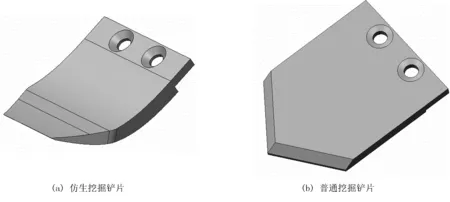
图4 两种挖掘铲片三维模型Fig.4 Two kinds of 3D model of digging shovel

2 仿生挖掘铲片减阻特性研究

为了对比分析仿生挖掘铲片与普通挖掘铲片在土壤介质中的切削阻力，应用离散元软件EDEM对两种挖掘铲铲片模型进行土壤切削阻力数值模拟，获取相关的力学分析数据，揭示挖掘铲片在土壤中运动的整个过程中两者的相互作用关系。

2.1 土壤颗粒力学模型建立

本文主要针对西南地区含水率在15%～20%之间的粘湿土壤进行仿真，真实的土壤所表现出来的复杂的非线性力学行为可以通过线性刚度模型、滑移模型和粘结约束模型根据含水率大小进行有机的组合来实现。下面主要对湿颗粒的液桥态和其所相对应的粘结约束模型进行介绍，不再对其它两种模型进行赘述。

根据不同地区土壤含水率不同，可以将土壤颗粒模型分为干颗粒模型和湿颗粒模型。其中，湿颗粒模型又分为液桥模型和浸渍模型两种形态。

水分是土壤的重要组成部分，土壤中的液态水根据饱和程度不同，通常以吸湿水和毛管水的状态存在。其中，毛管水在土壤颗粒空隙之间以摆动状态存在，在摆动状态下，土壤颗粒之间的水分呈不连续的液桥分布[8]。

R.A.Fisher认为，颗粒之间的液桥可以近似地看作是由两个相互垂直的弧面组成，两颗粒之间的液桥模型如图5(a)所示。粘湿土壤颗粒空隙之间不连续的液桥会产生“静态”毛细管力和“动态”粘附力。其中，ρ1、ρ2分别为凹面和凸面的半径，R1、R2为两颗粒半径；S1、S2为两颗粒到液桥颈部的距离；θ为颗粒的水接触角；Φ1、Φ2为两颗粒的嵌入角[9]。

颗粒模型之间的黏结约束是颗粒流理论中描述两颗粒之间一定尺度黏结物质的本构特性。线性刚度模型和滑移模型中并没有用来表征黏结特性的粘结模型，所以不能够作为仿真力学模型的选取对象；而粘结约束模型利用了并行约束原理在两个颗粒之间建立并行约束，组成非线性力学模型，如图5(b)所示。

在此模型中，土壤颗粒的性能方程表示为：[F]=[Fc]+[Fs]+[Fpb]+[Fd]。其中，F为土壤颗粒的综合作用力；Fc为土壤颗粒的接触合力；Fs为土壤颗粒摩擦力；Fpb为并行约束合力；Fd为粘性阻尼合力。

由于仿真对象的土壤颗粒的含水率在15%～20%之间，上述粘结约束模型虽不能完全准确地描述真实的粘湿土壤颗粒之间由于水分的存在而产生的黏结作用，但已经是最接近的了，为接下来在EDEM参数设定中选择颗粒之间的接触模型提供依据。软件中，仿真土壤颗粒之间的接触模型采用Hertz-Mindlin with bonding模型。因为该模型有粘结参数的设置，且与上述理论中的粘结约束模型形成对应关系，法向刚度对应接触法向弹簧，剪切刚度对应接触切向弹簧，临界剪切应力对应非张力联结，临界应力对应并行约束弹簧，通过粘接半径的设置来体现含水率对粘结约束的影响，这样更接近实际。

图5 液桥型的湿颗粒的力学模型Fig.5 Mechanical model of wet particles in liquid bridge type

2.2 仿生挖掘铲片离散元模型建立

本文应用CREO2.0进行挖掘铲仿真模型的三维建模，并对盛放土壤的土槽进行建模，然后将模型以IGES的格式导入 EDEM软件。

通过土壤的基本物理性能试验和模拟土壤的双轴试验、直剪试验获得如表1所示的仿真参数。其中，挖掘铲的材料选择采用65Mn[10]。

表1 EDEM仿真参数设置Table 1 EDEM simulation parameter setting

EDEM前处理器模块依次进行接触力学模型、仿真参数、土壤颗粒模型、几何模型和颗粒工厂等的设置。仿真试验为对比试验，所有参数设置不变，只改变两次仿真的对象(即挖掘铲片)。在EDEM求解器模块对仿真时步、仿真时间、数据保存间隔时间及网格大小等进行设置。仿真开始时生成土壤颗粒，待颗粒沉降稳定后挖掘铲开始运动，直至仿真结束。在EDEM后处理工具模块进行仿真结果的分析和导出。

仿真中，采用长为1m、宽为0.2m、高为0.2m、厚度为5mm的土槽，土壤颗粒之间的接触模型采用Hertz-Mindlin with bonding模型，颗粒生成方式为static，这样能够尽量减少计算机的运算。挖掘铲的动力学参数为：开始运动时间0.5s，结束时间2.5s，挖掘前进速度0.8m/s。为了让仿真的土壤更接近真实，让其先沉降0.5s，设置0.5s后土壤颗粒开始粘结。粘结参数为：法向接触刚度为1e+08，切向接触刚度为5e+07，临界法向切应力为30 000Pa，临界切向应力为15 000Pa；颗粒半径为4mm，设置粘结半径为5.2mm；仿真时间设置为2.5s，数据保存间隔为0.01s，网格尺寸设置为最小颗粒半径的2倍。

2.3 土壤分布状态

图6所示为两种挖掘铲初始仿真状态图。挖掘铲的入土角度均为30°，沿-X方向进行挖削，挖掘深度为90mm。为了分析不同挖掘铲在挖掘土壤过程中对土壤的扰动和所受阻力差异，将土壤设置为表层、浅层、中层、挖掘铲上层及挖掘铲下层共5层结构，依次深度为20、10、20、100、30mm，并在不同深度土层设置特定颜色的土壤颗粒，用于观察挖掘铲对土壤的扰动和土壤在挖掘铲上铲面的流变情况。

图6 两种挖掘铲仿真初始状态图Fig.6 Simulated initial state diagram of digging shovel

3 结果与分析

3.1 挖掘土壤扰动情况分析

从整个仿真过程中选取4个仿真时刻来观察铲面土壤动态扰动行为，即t1=0.57s、t2=0.63s、t3=0.72s和t4=0.78s。仿真过程中，为了清晰、直观地观察不同深度层土壤的扰动和流动，特将土壤进行颜色分层处理：表层、中层和挖掘铲下层作为参考层，颜色设置为浅色；浅层和挖掘铲上层为标记层，颜色设置为深色。

仿生挖掘铲切削土壤的过程大致可分为4个阶段，即切入阶段、切开阶段、上升阶段和持续性挖掘阶段，如图7所示。在0.57s时，挖掘过程处于切入阶段，由于沉降了0.5s，此时土壤层已变得不规则，铲尖刚切入挖掘铲下层，由于仿生挖掘铲铲尖为仿生曲面，铲尖处切削土壤切口较小、过渡大，位于浅层和挖掘铲上层的标记层基本无扰动；在0.63s时，挖掘过程处于切开阶段，此时铲片大部分已切入土壤，被切开的土壤堆积在仿生挖掘铲的铲面上，铲面上方的标记层和参考层交错在一起，扰动情况较明显；在0.72s时，挖掘过程处于上升阶段，随着挖掘的进行，堆积在铲面的土壤在后续进入铲面的土壤的推力下沿着仿生挖掘铲面向后上方运动，土壤标记层和参考层交错在一起，铲面土壤扰动情况明显；在0.78s时，挖掘铲处于持续性挖掘阶段，土壤切口较大，被切开的土壤沿着铲面持续上升直至从铲面后端掉落，铲尖处标记层和参考层无明显交错，扰动小，铲面土壤扰动已趋于稳定。

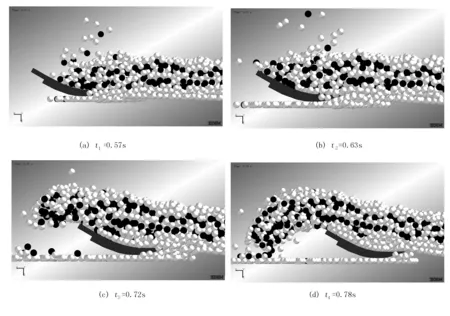
图7 仿生铲面土壤动态扰动行为模拟Fig.7 Simulation of soil dynamic disturbance in bionic shovel surface

从仿生挖掘铲挖掘土壤的整个仿真过程分析可知：由于仿生挖掘铲铲尖为曲面，挖削土壤切口小，过渡大，铲尖所受应力较分散，对土壤基本无扰动，推测出铲尖碎土能力一般。土壤沿铲面上升的过程中，运动路径类似于一个被“折弯”的过程，土壤扰动情况明显，推测出仿生铲面碎土能力良好。

同理，普通挖掘铲挖掘土壤的过程也大致分为4个阶段，即切入阶段、切开阶段、上升阶段、持续性挖掘阶段，如图8所示。在0.57s时，挖掘过程处于切入阶段，由于沉降了0.5s，此时土壤层已变得不规则，此时铲尖刚切入挖掘铲下层，铲尖处切削土壤切口较大、过渡小，位于浅层和挖掘铲上层的标记层扰动明显；在0.63s时，挖掘过程处于切开阶段，此时铲片大部分已切入土壤，被切开的土壤堆积在普通挖掘铲的铲面上，扰动情况明显；在0.72s时，挖掘过程处于上升阶段，随着挖掘的进行，堆积在铲面的土壤在后续进入铲面土壤的推力下沿着普通挖掘铲面向后上方运动，由于普通挖掘铲铲面为平面，整个运动基本为平移运动，扰动情况明显；在0.78s时，挖掘铲处于持续性挖掘阶段，土壤切口较大，被切开的土壤沿着铲面持续上升，扰动情况明显。

图8 普通铲面土壤动态扰动行为模拟Fig.8 Simulation of soil dynamic disturbance in ordinary shovel surface

从普通挖掘铲挖掘土壤的整个仿真过程分析可知：由于普通挖掘铲铲尖和铲面均为平面，挖削土壤切口较大、过渡小，铲尖所受应力较集中，对土壤扰动明显，推测出铲尖碎土能力良好；土壤沿铲面上升的过程中，运动路径为平移运动，且后续的3个阶段土壤扰动情况相对于第1阶段均无较大变化，推测出普通铲面不具备碎土能力。

3.2 挖掘铲挖掘阻力分析

运用离散元法对两种挖掘铲片在相同的条件参数设置下挖掘土壤的过程进行仿真，得到两种挖掘铲片所受挖掘阻力随时间变化的曲线，如图9所示。

由仿生挖掘铲片所受挖掘阻力曲线可以看出：由于事先设置的土壤沉降时间为0.5s，铲片在刚开始的0.5s内阻力为零，然后铲片开始运动。切入阶段过程中，铲尖切开土壤，阻力逐渐增大；切开阶段过程中，土壤堆积在仿生挖掘铲的铲面上，阻力继续增大；在上升阶段过程中，土壤扰动情况明显，“折弯”过程使得挖掘铲所受阻力出现了小范围的波动，在持续性挖掘阶段过程中，土壤不断地沿铲尖进入铲面，从铲面掉落，但进入的土壤是连续性的，而掉落的土壤却呈现出不规律的短时周期性，所以这个过程中挖掘铲所受阻力曲线为大致稳定的波动折线。

由普通挖掘铲片所受挖掘阻力曲线可以看出：由于土壤沉降时间为0.5s，铲片在刚开始的0.5s内阻力为零，然后铲片开始运动。切入阶段过程中，铲尖切开土壤，阻力逐渐增大；切开阶段过程中，土壤堆积在普通挖掘铲的铲面上，阻力继续增大；在上升阶段过程中，挖掘阻力达到最大；在持续性挖掘阶段过程中，土壤不断的沿铲尖进入铲面，然后从铲面掉落，但进入的土壤是连续性的，而掉落的土壤却呈现出不规律的短时周期性，所以这个过程中挖掘铲所受阻力曲线为大致稳定的波动折线。

图9 两种挖掘铲片受力曲线Fig.9 Resistance curve of two kinds of digging shovel

从仿生挖掘铲片和普通挖掘铲片挖削土壤时的阻力曲线对比可以看出：在切入阶段和切开阶段，仿生挖掘铲铲尖为曲面，挖削土壤切口小，过渡大，应力较分散，而普通挖掘铲反之，所以仿生挖掘铲所受阻力曲线的斜率略小于普通挖掘铲；在上升阶段，仿生挖掘铲铲面具有“折弯”土壤的过程，而土壤在普通挖掘铲面上升中做平移运动，所以仿生挖掘铲所受阻力出现小范围的波动，而此时普通挖掘铲所受阻力达到最大值；在持续性挖掘阶段，两种挖掘铲所受阻力均呈周期性波动。

将0.5s直至仿真结束时间段内阻力点值求平均值，得到仿生挖掘铲片的平均阻力为118.212N，普通挖掘铲片的平均阻力为159.508N，仿生铲片较普通铲片挖削土壤时的阻力减小近26%。