胶层对内贴CFRP加固圆形隧洞受力特性的影响
2019-12-21曹生荣
秦 敢,曹生荣,杨 帆
胶层对内贴CFRP加固圆形隧洞受力特性的影响
秦 敢,曹生荣,杨 帆
(武汉大学水资源与水电工程科学国家重点实验室,武汉 430072)
基于CFRP加固圆形隧洞的小比例尺模型试验,采用实体单元模拟胶层和衬砌混凝土,采用弹簧单元以及双线性界面黏结滑移关系模拟胶层和衬砌混凝土的弧形接触界面的黏结滑移行为,建立了“实体-弹簧-实体”三维有限元模型,并将有限元模型的计算结果与模型试验的实测结果以及界面应力理论计算结果进行了对比,验证了三维有限元模型的有效性.基于该有限元模型,着重分析了胶层厚度以及弹性模量的变化对混凝土应力、CFRP应力、胶层应力以及弧形接触界面复杂应力状态的影响.计算分析结果表明:胶层厚度以及弹性模量对隧洞衬砌混凝土的应力水平无明显影响,改变胶层的厚度以及弹性模量并不能明显地改善衬砌混凝土的受力状态;胶层的厚度以及弹性模量对弧形接触界面应力的影响十分显著,选择弹性模量较小的胶层,在施工过程中适当地减薄胶层的涂刷厚度,可以显著降低界面应力,从而减小内贴CFRP加固圆形隧洞结构发生剥离破坏的风险.
圆形隧洞;CFRP;黏结滑移;胶层;受力特性;有限元模型
碳纤维增强复合材料(carbon fiber reinforced polymer,CFRP)具有自重轻、抗拉强度高以及耐腐蚀性能好等优点[1],作为抗拉材料能有效地控制衬砌裂缝的继续扩展,防止衬砌掉块、剥落,在隧洞补强加固中具有广泛的应用前景[2-3].如表1所示,内贴CFRP加固在桃花江水库、青山水库以及大伙房水库等工程的圆形输水隧洞中已经得到了良好应用.
表1 内贴CFRP加固输水隧洞实例

Tab.1 Examples of tunnels strengthened with CFRP
采用CFRP加固圆形隧洞时,是通过黏胶将CFRP粘贴于衬砌混凝土的内表面,并通过黏胶传递应力使CFRP能够参与承载.因而,胶层是保证CFRP与衬砌混凝土两种材料能够共同工作的基础.目前,针对内贴CFRP加固圆形隧洞结构的研究,主要以室内模型试验以及数值模拟为主,分析内容大多针对特定病害的CFRP补强加固效果[4]、衬砌混凝土的损伤历时对加固效果的影响[5]以及相关加固参数的优化[6-7]等.在工程实践中,不同种类的胶层固化后的弹性模量不同,胶层涂刷的厚度也因操作人员的不同而差别较大[8].胶层弹性模量以及厚度的差异对衬砌混凝土的受力以及CFRP的受力的影响如何鲜见报道.
目前,有关CFRP加固混凝土结构中的“胶层”的研究,主要是针对混凝土梁的CFRP抗弯加固或者抗剪加固而展开,分析内容大多针对胶层的厚度以及弹性模量对胶层和混凝土接触界面黏结滑移行为的影响.杜运兴等[9]、López-González等[10]、钟正强 等[11]和Edalati等[12]的计算结果表明,胶层是影响界面应力大小以及界面剥离破坏的重要因素.对于混凝土梁的CFRP抗弯加固和抗剪加固,胶层与混凝土的接触界面为平面,界面的黏结应力也主要为剪应 力[13-14].通过胶层传递的界面剪应力使梁底部或侧面粘贴的CFRP承担一部分截面弯矩或者剪力,从而提高混凝土梁的抗弯或抗剪承载力.
对于内贴CFRP加固圆形隧洞结构,加固界面为弧形曲面.Wang等[15]和de Lorenzis等[16]的研究表明,由于界面曲率的存在,使得胶层与混凝土的接触面上不仅存在界面剪应力,而且会存在界面正拉应力,界面正拉应力的存在会导致结构更早地发生剥离破坏.与混凝土梁的CFRP抗弯加固或者抗剪加固
相比而言,隧洞结构的施工过程、工作环境、结构形式、荷载特点等复杂度更高,弧形加固界面的应力状态也比平面加固界面更为复杂.而胶层对弧形界面复杂应力状态的影响规律如何,至今也缺乏相关方面的探讨.
由于模型试验对试验设备和试验成本的要求较高,有限元方法作为一种有效的替代工具,在结构应力的计算以及相关参数的分析中得到了广泛使用[17].因此,本文采用有限元方法对上述问题展开分析.首先,详细阐述了CFRP加固圆形隧洞结构的有限元建模方法,包括单元的选取、弧形界面黏结滑移行为的模拟等.并将有限元模型的计算结果与垂直荷载条件下CFRP加固圆形隧洞的小比例尺模型试验的实测结果以及界面应力理论计算结果进行了对比分析,验证了有限元模型的有效性.在此基础上,分析了胶层厚度以及弹性模量的改变对混凝土应力、CFRP应力、胶层应力以及弧形界面复杂界面应力状态的影响规律,并从提升CFRP材料的承载效率、减小界面应力防止剥离等角度对上述加固参数进行优化,以期为内贴CFRP加固圆形隧洞的加固方案设计以及施工方案的优化提供指导和借鉴.
1 模型试验概况
王利阳[18]采用小比例尺模型试验,研究了在垂直荷载条件下内贴CFRP加固圆形隧洞的加固效果.试验总共包含5个试件,其中2个试件为对比试件,未粘贴CFRP,3个试件在混凝土内表面满粘CFRP.试件采用C30混凝土制作,内径为300,mm,厚度为30,mm,纵向长度为1,000,mm.在试件纵向配有6根直径为4,mm的架立钢筋,架立钢筋沿试件环向间隔60°布置.试件环向配有直径为3,mm的螺旋箍筋,螺旋箍筋的间距为74,mm.试件的加载方式如图1所示.试件的材料参数如表2所示.在试验过程中,为了充分了解混凝土以及CFRP的应力应变情况,在混凝土内外表面以及CFRP上布置了一定数量的应变片,应变片的分布情况如图2所示.

图1 荷载施加示意(单位:mm)
表2 材料参数

Tab.2 Parameters of material

图2 应变片分布
2 有限元模型
本文采用有限元软件ANSYS对上述小比例尺模型试验进行建模分析.有限元模型如图3所示.混凝土采用Solid 65单元模拟,受拉区混凝土采用线弹性的应力应变关系,受压区混凝土的应力应变关系由式(1)~(3)计算[19].
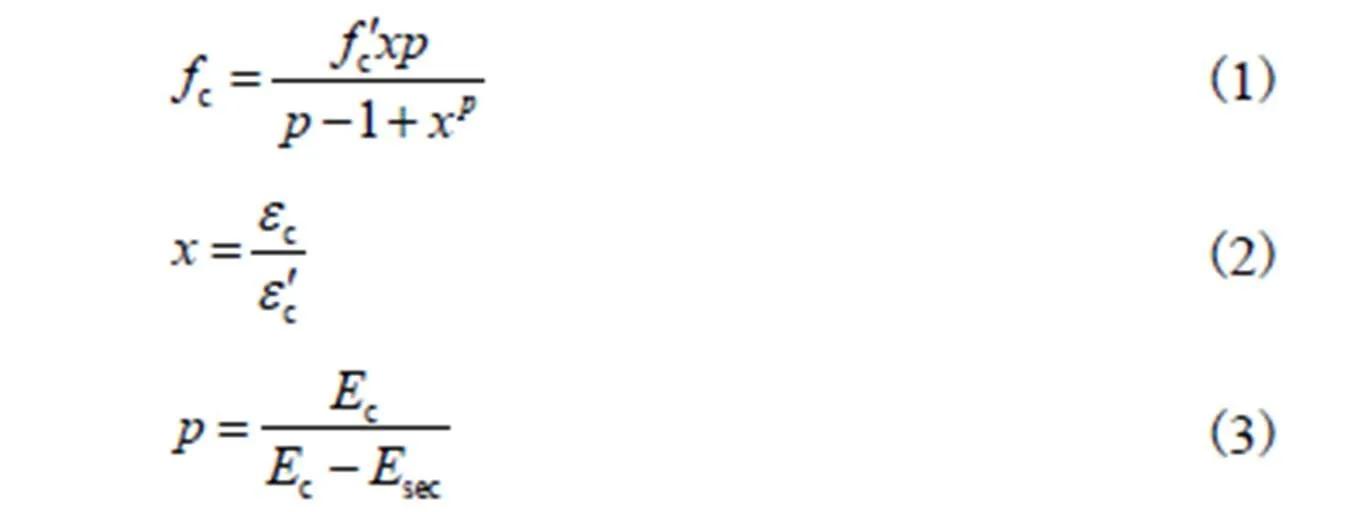
式中:fc是在任意压应变εc条件下的混凝土压应力;是混凝土处于极限抗压强度时所对应的应变;Ec和Esec分别是混凝土的切线模量和割线模量.如图4(a)所示,当混凝土的主应力超过混凝土的极限抗压强度时,随着混凝土应变的增加,混凝土的应力将不会发生变化.

图4 材料的本构关系
钢筋采用Link 8单元模拟,在钢筋屈服前应力应变关系为线弹性.钢筋屈服后,其塑性模量(sp)为弹性模量(se)的1%,,如图4(b)所示.钢筋和混凝土之间按共节点处理,不考虑钢筋和混凝土的黏结滑移.采用Solid 45实体单元模拟胶层,采用Shell 63单元模拟CFRP,CFRP和胶层均简化为线弹性材料,胶层的各项性能参数如表3所示.
表3 胶层性能参数

Tab.3 Performance parameters of adhesive layer
对于常见的湿作业粘贴CFRP,由于胶层和CFRP之间很难清晰地加以区分,故在有限元建模过程中,常常不考虑胶层的作用,使用CFRP的名义厚度和弹性模量来建立有限元模型,如图5(a)所示.CFRP和衬砌混凝土之间通过插入界面弹簧单元来表征胶层的传力作用以及界面的黏结滑移.但不考虑胶层的界面弹簧模型存在以下问题:①弹簧单元为无厚度的界面单元,该模型无法分析胶层厚度对结构受力以及界面滑移行为的影响;②无法反映沿胶层厚度方向界面应力的变化规律;③胶层的材料参数(如弹性模量)只能通过黏结滑移本构关系来表征,当改变胶层的材料参数时,该模型只能通过修正黏结滑移本构关系来反映胶层材料参数的变化给结构带来的影响,这也给有限元分析带来了极大的不便.

图5 界面模拟示意
为此,本文在有限元模型中采用实体单元模拟胶层,采用弹簧单元模拟胶层和衬砌混凝土接触界面的黏结滑移行为,建立“实体-弹簧-实体”三维有限元模型.弹簧的一端连接胶层单元节点,另一端连接混凝土单元节点,如图5(b)所示.每个相对应的节点间由径向弹簧和切向弹簧连接,分别代表连接面径向和切向的相互作用.每根弹簧的刚度为弹簧的力-位移关系曲线(曲线)的一阶倒数,即

式中:t为切向弹簧的刚度;n为径向弹簧的刚度;A为第根弹簧在界面上代表的受力面积;t为接触界面切向黏结滑移本构关系;n为接触界面径向黏结滑移本构关系.
如图6所示,双线性黏结滑移模型表达形式简单,可以较好地把握胶层和混凝土接触界面黏结滑移关系的基本特征,反映接触界面的界面黏结强度(即n,max和t,max)以及界面破坏能(即黏结滑移曲线包围的面积),是模拟CFRP与混凝土的界面行为最常用的模型[20].因此,本文选择双线性黏结滑移模型作为接触界面切向和径向的黏结滑移本构关系,t和n的表达式分别如式(8)和(9)所示.

(a)切向黏结滑移关系 (b)径向黏结滑移关系
图6 界面黏结滑移模型
Fig.6 Interfacial bond-slip model
3 结果对比及模型验证
3.1 与模型试验对比
对前述试验中在垂直荷载作用下的混凝土试件进行非线性有限元分析,并将计算得出的混凝土试件内外表面以及CFRP上的应变变化规律同实测试验结果进行对比.因为混凝土试件为轴对称结构,故仅将0°(拱顶)和90°(拱腰)位置的计算结果和实测结果进行比较.图7为混凝土环向微应变的对比情况,图8为CFRP环向微应变的对比情况.
由图7和图8可见,计算结果与实测结果虽然存在一定程度的差异,但有限元模型计算得出的应变变化规律同实测数据所反映的变化规律基本一致.考虑到模型试验实测结果的可靠性可能受到仪器布置、测量精度以及试验边界条件不理想等因素的影响,有限元计算结果的可靠性也可能受到网格剖分、材料本构关系与实际情况存在一定差异等因素的影响,图7和图8计算结果与实测结果的差异可以认为处于工程可接受范围,由此也说明了“实体-弹簧-实体”模型的有效性.

图7 混凝土环向微应变

图8 CFRP环向微应变
3.2 与理论分析对比
针对CFRP加固曲面混凝土结构,Zhang等[22]推导出了薄板加固曲面形状混凝土结构在任意边界条件下的界面应力解析解.由于胶层和混凝土接触界面的界面应力很难由室内试验测得,为了分析上述“实体-弹簧-实体”有限元模型能否准确地模拟胶层和混凝土接触界面的界面应力发展规律,故将文献[22]中的算例进行有限元建模分析,并与理论的解析解进行分析比较.计算算例如图9所示,曲梁的半径=2,m,梁宽1为200,mm,高度1为300,mm;CFRP的粘贴宽度2为200,mm,胶层的厚度a为2,mm.梁的中部承担有=150,kN的集中力荷载.计算结果对比情况如图10~11所示.由图10和图11可见,有限元模型计算得出的界面黏结剪应力和黏结正应力同理论解析模型的计算结果吻合较好,说明本文选用的双线性黏结滑移模型合适,界面峰值应力等参数的选择合理,“实体-弹簧-实体”模型能够较好地反映胶层和混凝土接触界面的受力特性,可以用于后续的分析研究中.

图9 计算算例
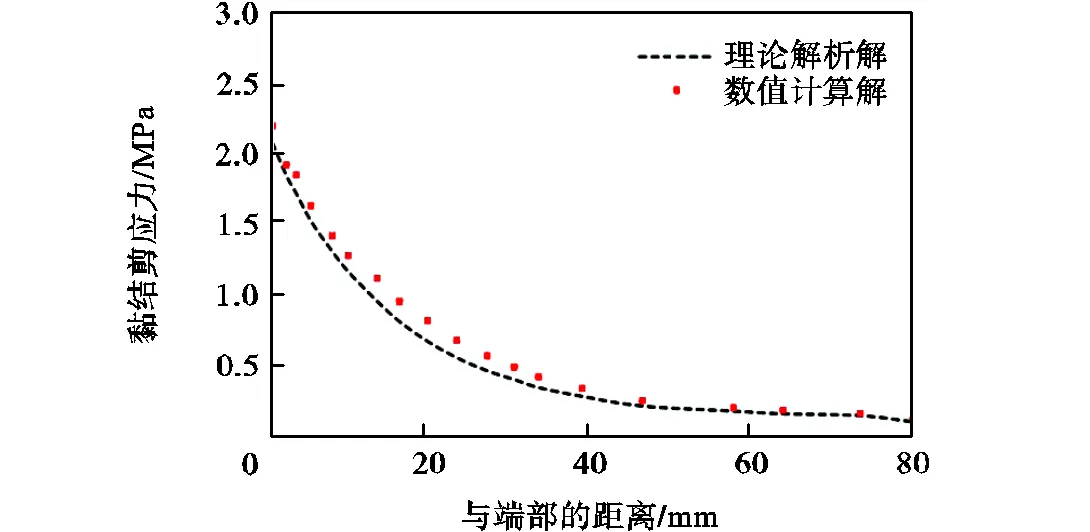
图10 界面黏结剪应力

图11 界面黏结正应力
4 计算结果及分析
鉴于大多数工程实践中不同种类胶层的弹性模量在0.24~11.20,GPa间变化,涂刷的厚度在1~4,mm间变化[8],因此,在后文的分析中,分别选取=0.24,GPa、2.00,GPa、11.20,GPa以及=1,mm、2,mm、4,mm等6种工况进行分别的计算,计算结果如图12~16所示.
4.1 对混凝土环向应力的影响
由图12可知,随着胶层厚度的增加,混凝土内表面环向应力的分布特征没有发生明显改变,混凝土内表面环向最大拉应力由2.05,MPa逐渐减小到1.95,MPa,减小幅度为4.9%,.随着胶层弹性模量的增加,混凝土内表面环向应力的分布特征也没有发生明显改变,混凝土内表面环向最大拉应力由2.07,MPa逐渐减小到1.90,MPa,减小幅度为5.1%. 由以上分析可知,胶层对衬砌混凝土应力水平的影响十分有限,改变胶层厚度以及弹性模量并不能明显地改善衬砌混凝土的受力状态.
4.2 对CFRP环向应力的影响
由图13可知,随着胶层的厚度以及弹性模量的变化,CFRP的环向应力的分布特征没有发生改变,CFRP的最大环向拉应力在15~19,MPa之间变化.CFRP的应力水平远低于CFRP的抗拉强度,CFRP材料的抗拉性能并没有被充分利用和发挥.综合图12~13的分析可知,采用CFRP加固圆形隧洞时,CFRP能够帮衬砌混凝土承担一部分外部荷载,但承载性能发挥程度有限.仅仅通过改变胶层厚度或者选择不同弹性模量的胶层并不能明显地改变衬砌混凝土和CFRP之间的承载比例.
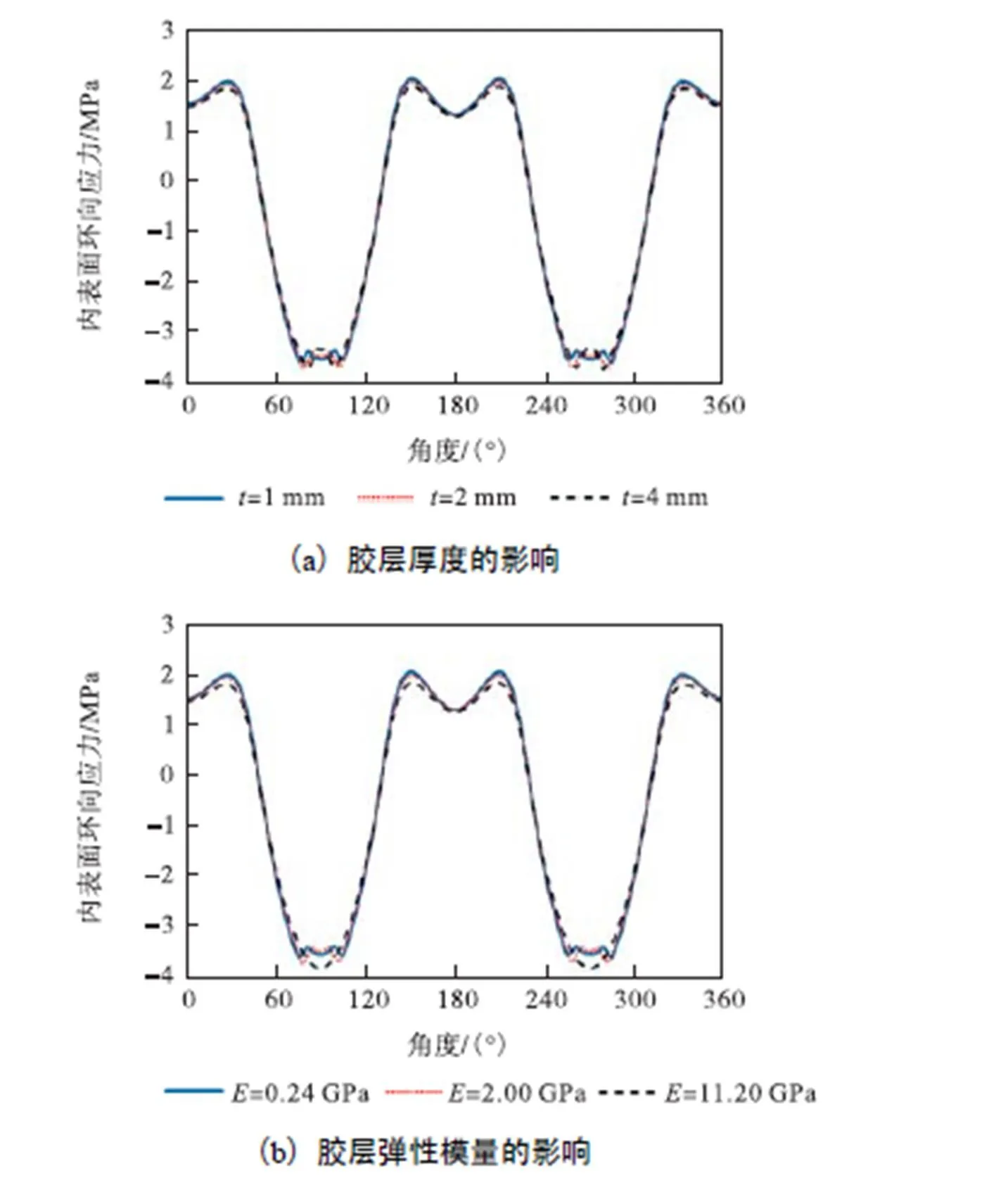
图12 混凝土内表面环向应力

图13 CFRP环向应力
4.3 对胶层环向应力的影响
图14所示为胶层厚度以及弹性模量的变化对胶层环向应力的影响.由图14可知,胶层厚度对其环向应力的影响并不明显;但随着胶层弹性模量的增加,受拉区的胶层应力以及受压区的胶层应力均出现了明显增长.虽然胶层弹性模量对胶层环向应力的影响十分显著,但由表3可知,胶层和混凝土接触界面的黏结强度约为胶层抗拉强度的1/10,胶层并不是内贴CFRP加固混凝土结构中的薄弱环节.现有的大量研究也表明,在施工条件可靠的情况下,胶层内部的撕裂破坏一般不会发生,更为常见的是因界面应力过大引起保护层混凝土撕裂而导致的剥离破坏[23].
4.4 对界面应力的影响
从图15(a)可以看出,随着胶层厚度的逐渐增加,界面径向应力的分布规律没有发生明显改变,界面径向受拉区的范围也没有明显扩大.但受拉区径向应力的大小和受压区径向应力的大小均随着胶层厚度的增加而逐渐增大.在胶层厚度由1,mm逐渐增加到4,mm的过程中,界面最大径向拉应力由0.011,MPa逐渐增加到0.016,MPa,增加幅度为45.5%,.从图15(b)可以看出,随着胶层厚度的逐渐增加,界面环向应力的分布规律没有发生明显改变,但界面环向应力的大小明显增加.在胶层厚度由1,mm逐渐增加到4,mm的过程中,界面最大环向应力由0.056,MPa逐渐增加到0.079,MPa,增加幅度为41.1%,.综合图15(a)和图15(b)的分析可知,胶层厚度对界面应力的影响很大.从减小界面应力防止剥离的角度出发,减薄胶层的厚度有利于降低胶层和混凝土界面的径向应力和环向应力,对CFRP与衬砌混凝土的长期共同作用有利.
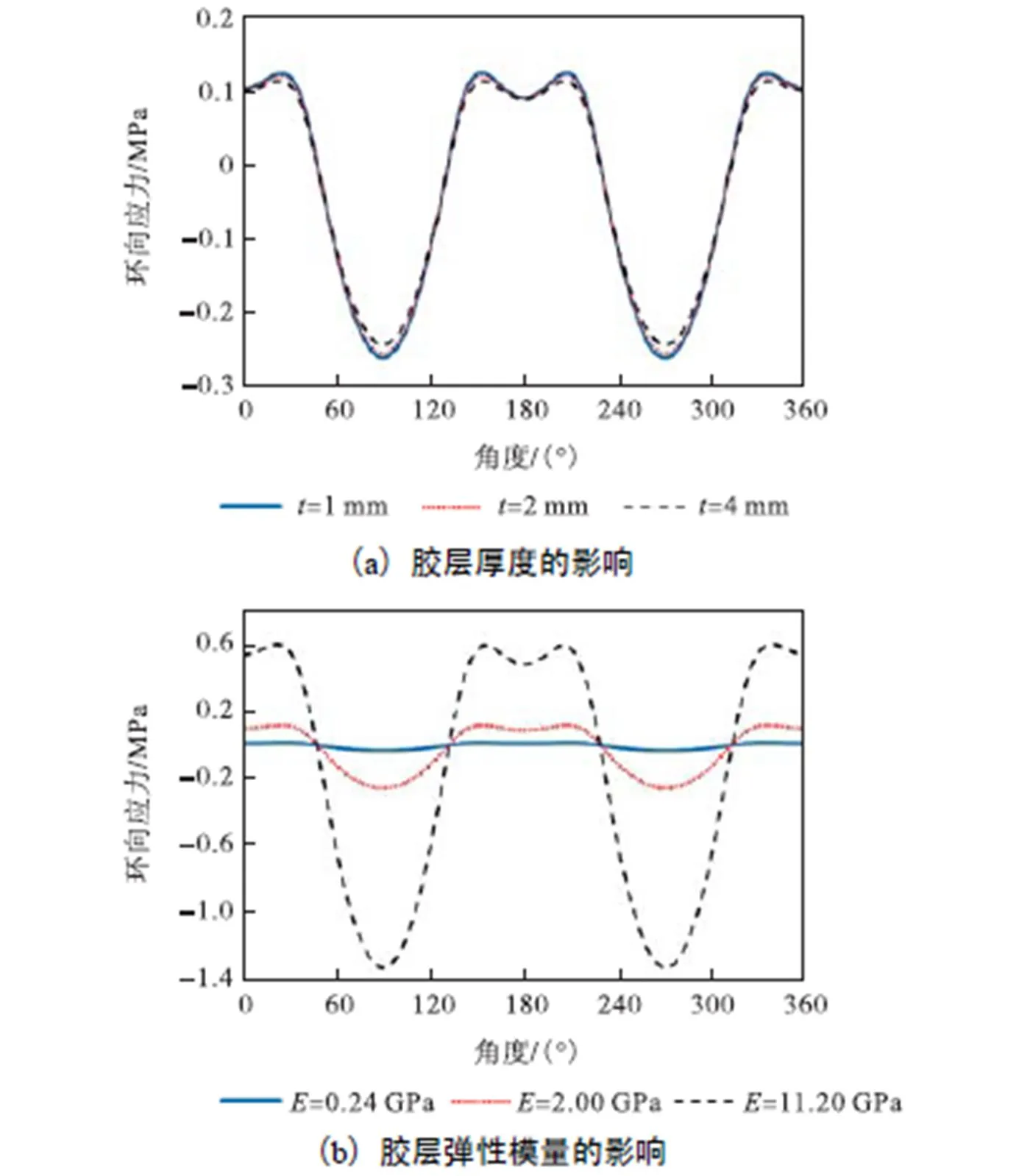
图14 胶层环向应力

图15 胶层厚度对界面应力的影响

图16 胶层弹性模量对界面应力的影响
从图16(a)可以看出,随着胶层弹性模量的增加,界面径向应力的分布规律没有发生明显改变,界面径向受拉区的范围也没有明显扩大.但受拉区径向应力的大小和受压区径向应力的大小均随着胶层弹性模量的提高而逐渐增大.在胶层的弹性模量由0.24,GPa变化到11.20,GPa的过程中,界面最大径向拉应力由0.011,MPa逐渐增加到0.020,MPa,增加幅度为81.8%,.界面径向拉应力的增加会导致结构过早地出现剥离.
从图16(b)可以看出,随着胶层弹性模量的逐渐增加,界面环向应力的分布规律没有发生明显改变,但界面环向应力的大小明显增加.在胶层的弹性模量由0.24,GPa变化到11.20,GPa的过程中,界面最大环向应力由0.053,MPa逐渐增加到0.098,MPa,增加幅度为84.9%,.综合图16(a)和图16(b)的分析可知,胶层的弹性模量对胶层和衬砌混凝土接触界面的界面应力影响很大.在工程实践中,采用内贴CFRP对圆形隧洞衬砌混凝土结构进行加固时,选择弹性模量较小的胶层种类可以减小界面的径向应力和环向应力,从而降低结构发生剥离破坏的风险.
5 结 论
(1) 试验对比分析以及理论对比分析表明,“实体-弹簧-实体”有限元模型能较好地模拟衬砌混凝土、CFRP以及胶层和衬砌混凝土接触界面的应力发展规律,该模型具有很好的可推广性,可适用于分析CFRP加固输水隧洞的各类问题.
(2) 胶层的厚度以及弹性模量对隧洞衬砌混凝土的应力水平无明显影响.在胶层厚度由1,mm逐渐增加到4,mm的过程中,混凝土的最大拉应力的减小幅度仅为4.9%,.在胶层的弹性模量由0.24,GPa变化到11.20,GPa的过程中,混凝土的最大拉应力的减小幅度仅为5.1%,.通过改变胶层厚度或者选择不同弹性模量的胶层等方法不能明显地改善衬砌混凝土的受力状态.
(3) 采用内贴CFRP加固圆形输水隧洞时,CFRP能够帮助衬砌混凝土承担部分外部荷载,但承载比例有限,CFRP的抗拉性能很难被充分发挥.通过改变胶层厚度或者选择不同弹性模量的胶层等方法不能明显地提高CFRP的承载效率.
(4) 胶层的厚度以及弹性模量对弧形接触界面应力状态的影响十分显著.在胶层厚度由1,mm逐渐增加到4,mm的过程中,界面最大径向拉应力的增加幅度超过了45%.在胶层的弹性模量由0.24,GPa变化到11.20,GPa的过程中,界面最大径向拉应力的增加幅度超过了80%.胶层对弧形界面界面应力影响的分析结果表明,采用内贴CFRP加固圆形隧洞结构时,选择弹性模量较小的胶层,在施工过程中适当地减薄胶层的涂刷厚度,可以显著降低界面应力,从而减小内贴CFRP加固圆形隧洞结构发生剥离破坏的风险.
[1] Wang Tiecheng,Yu Liu,Wang Lijun. Numerical determination of shear strength of steel reinforced concrete column strengthened by CFRP sheets[J]. Transactions of Tianjin University,2003,9(1):58-62.
[2] Liu D,Huang H,Yue Q,et al. Behaviour of tunnel lining strengthened by textile-reinforced concrete[J]. Structure and Infrastructure Engineering,2016,12(8):964-976.
[3] Wang T T,Lee C H. Life-cycle design considerations for hydraulic tunnels:Lessons learned from inspection and maintenance cases[J]. Journal of Performance of Constructed Facilities,2012,27(6):796-806.
[4] 何 川,唐志成,汪 波,等. 内表面补强对缺陷病害隧道结构承载力影响的模型试验研究[J]. 岩土力学,2009,30(2):406-412. He Chuan,Tang Zhicheng,Wang Bo,et al. Research on effect of inner surface reinforcing on structure bearing capacity by model test in defective tunnel[J]. Rock and Soil Mechanics,2009,30(2):406-412(in Chinese).
[5] 刘 飞. 地下管道灾后应急处置加固技术研究[D]. 大连:大连理工大学土木工程学院,2009.Liu Fei. Study on Post-Earthquake Emergency Pipeline Reinforcement[D]. Dalian:School of Civil Engineering,Dalian University of Technology,2009(in Chinese).
[6] 罗立娜. 碳纤维补强条件下公路隧道衬砌计算方法的研究[D]. 上海:同济大学土木工程学院,2006. Luo Lina. Study on the Calculation Method of CFRP Strengthened Highway Tunnel Lining[D]. Shanghai:School of Civil Engineering,Tongji University,2006(in Chinese).
[7] 周大举. 基于可靠度理论的碳纤维加固公路隧道衬砌计算方法研究[D]. 上海:同济大学土木工程学院,2008. Zhou Daju. Calculation Method of CFRP Strengthened Highway Tunnel Lining Based on Reliability Theories [D]. Shanghai:School of Civil Engineering,Tongji University,2008(in Chinese).
[8] Dai J G,Ueda T. Local bond stress slip relations for FRP sheets-concrete interfaces[C] //Proceedings of 6th International Symposium on FRP Reinforcement for Concrete Structures. Singapore,2003:143-152.
[9] 杜运兴,侯春旭,周 芬. 不均匀胶层对CFRP板加固梁的界面应力影响[J]. 湖南大学学报,2017,44(3):61-67. Du Yunxing,Hou Chunxu,Zhou Fen. Effect of uneven adhesive layer on interfacial stress of beams strengthened with CFRP plate[J]. Journal of Hunan University,2017,44(3):61-67(in Chinese).
[10] López-González J C,Fernández-Gómez J,González-Valle E. Effect of adhesive thickness and concrete strength on FRP-concrete bonds[J]. Journal of Composites for Construction,2012,16(6):705-711.
[11] 钟正强,喻 奕,刘 波. 胶层厚度对预应力CFRP加固混凝土梁粘结应力的影响试验[J]. 中国公路学报,2014,27(11):55-62. Zhong Zhengqiang,Yu Yi,Liu Bo. Experimental study on influence of adhesive layer thickness on bond stress of concrete beams strengthened with prestresses CFRP[J]. China Journal of Highway and Transport,2014,27(11):55-62(in Chinese).
[12] Edalati M,Irani F. Interfacial stresses in RC beams strengthened by externally bonded FRP/steel plates with effects of shear deformations[J]. Journal of Composites for Construction,2012,16(1):60-73.
[13] Monti G,Liotta M. Tests and design equations for FRP-strengthening in shear[J]. Construction and Building Materials,2007,21(4):799-809.
[14] Zhang L,Teng J G. Finite element prediction of interfacial stresses in structural members bonded with a thin plate[J]. Engineering Structures,2010,32(2):459-471.
[15] Wang J,Zhang C. A three-parameter elastic foundation model for interface stresses in curved beams externally strengthened by a thin FRP plate[J]. International Journal of Solids and Structures,2010,47(7):998-1006.
[16] De Lorenzis L,Teng J G,Zhang L. Interfacial stresses in curved members bonded with a thin plate[J]. International Journal of Solids and Structures,2006,43(25):7501-7517.
[17] 王铁成,白锡庆,赵海龙,等. CFRP加固钢筋混凝土框架动力时程分析[J]. 建筑结构学报,2015,36(增2):146-152. Wang Tiecheng,Bai Xiqing,Zhao Hailong,et al. Dynamic time-history analysis of RC frame strengthened with CFRP[J]. Journal of Building Structures,2015,36(Suppl 2):146-152(in Chinese).
[18] 王利阳. 纤维材料加固钢筋混凝土压力管道的试验研究[D]. 武汉:武汉大学土木建筑工程学院,2004(in Chinese). Wang Liyang. The Experimental Study on Pressure Conduit of Ferroconcrete Reinforced by Fabric Reinforced Plastic[D]. Wuhan:School of Civil Engineering,Wuhan University,2004(in Chinese).
[19] Popovics S. A numerical approach to the complete stress-strain curve of concrete[J]. Cement & Concrete Research,1973,3(5):583-599.
[20] 陆新征,叶列平,滕锦光,等. FRP-混凝土界面粘结滑移本构模型[J]. 建筑结构学报,2005,26(4):10-18. Lu Xinzheng,Ye Lieping,Teng Jinguang,et al. Bond-slip model for FRP-to-concrete interface[J]. Journal of Building Structures,2005,26(4):10-18(in Chinese).
[21] De Lorenzis L,Zavarise G. Interfacial stress analysis and prediction of debonding for a thin plate bonded to a curved substrate[J]. International Journal of Non-Linear Mechanics,2009,44(4):358-370.
[22] Zhang L,Teng J G. Simple general solution for interfacial stresses in plated beams[J]. Journal of Composites for Construction,2010,14(4):434-442.
[23] 陆新征. FRP-混凝土界面行为研究[D]. 北京:清华大学土木工程学院,2005. Lu Xinzheng. Study on FRP-Concrete Interface[D]. Beijing:School of Civil Engineering,Tsinghua University,2004(in Chinese).
Effect of Adhesive Layer on Mechanical Properties of Circular Tunnel Strengthened with CFRP
Qin Gan,Cao Shengrong,Yang Fan
(State Key Laboratory of Water Resources and Hydropower Engineering Science,Wuhan University,Wuhan 430072,China)
Based on the small scale model test of circular tunnel strengthened with CFRP,a “solid-spring-solid” three dimensional finite model is established. The adhesive layer and lining concrete is simulated by solid elements. The bond-slip behaviourof curved interface between adhesive layer and lining concrete is simulated by spring elements. The bilinear model is used to simulate the interfacial behaviour. Then,the calculation results of the finite element model are compared with the measured results from the small scale model test and the theoretical calculation results of interfacial stress,and the three dimensional finite element model is validated. Based on the finite element model,the effects of adhesive layer’s elasticitymodulus and the thickness on the stress of concrete,CFRP,adhesive layer and the complex stress state of curved contact interface are investigated. The calculation and analysis results reveal that the thickness and elasticitymodulusof the adhesive layer have little effect on the stress and strain of the lining concrete. Changing the thickness and elasticitymodulusof the adhesive layer cannot improve the stress state of lining concrete. However,they have an obvious effect on the interfacial stress of the curved contact interface. A soft adhesive layer or a thin adhesive layer can reduce the interfacial stress,thus reducing the risk of debonding failureof circular tunnel strengthened with CFRP.
circular tunnel;CFRP;bond-slip;adhesive layer;mechanical properties;finite element model
TV332
A
0493-2137(2019)01-0062-09
2018-03-23;
2018-05-28.
秦 敢(1989— ),男,博士研究生,gqin@whu.edu.cn.
曹生荣,shrcao@whu.edu.cn.
湖北省自然科学基金资助项目(2017CFB667);水文水资源与水利工程科学国家重点实验室开放基金资助项目(2015491711);国家自然科学基金资助项目(51079107).
the Natural Science Foundation of Hubei Province,China(No.2017CFB667),the State Key Laboratory of Hydrology and Water Resources and Hydraulic Engineering Foundation(No.2015494711),the National Natural Science Foundation of China (No.51079107).
10.11784/tdxbz201803082
(责任编辑:樊素英)
