优化模型在挤出吹塑工艺模拟中的运用

苏卫东 陈学宏

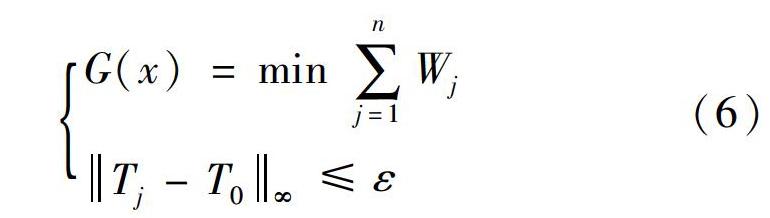
摘要：为减轻汽车塑料燃油箱的总质量，模拟挤出吹塑工艺中燃油箱的壁厚变化。将模拟问题分为3部分，即型坯长度优化、静态柔性变形板优化和垂直厚度分布系统优化。每个优化过程抽象为一个数学模型，在MATLAB中求解数学模型并获得最优解。优化结果与实际试验结果基本一致，产品总质量偏差小于3%，壁厚偏差小于7%，证明模拟方法合理。

关键词：燃油箱; 挤出吹塑; 数学模型; 壁厚; 优化

中图分类号：U463.221.6; TQ320.663; TP391.92

文献标志码：B

Application of optimization model in

extrusion blowing process simulation

SU Weidong， CHEN Xuehong

（Research and Development Center， YAPP Automotive Systems Co.， Ltd.， Yangzhou 225001， Jiangsu， China）

Abstract：

To reduce the total mass of automobile plastic fuel tank， the wall thickness change of fuel tank in extrusion blowing process is simulated. The simulation is divided into three parts， which are parison length optimization， static flexible deformation plate optimization， and vertical thickness distribution system optimization. Each optimization process is abstracted into a mathematic model. The mathematic model is solved by MATLAB， and the optimal solution is obtained. The optimization results agree well with the test results， the total product mass deviation is less than 3%， the wall thickness deviation is less than 7%. It is proved that the simulation method is reasonable.

Key words：

fuel tank; extrusion blowing process; mathematic model; wall thickness; optimization

收稿日期：2019-07-03

修回日期：2019-08-01

作者简介：

苏卫东（1972—），男，江苏扬州人，工程师，研究方向为车载燃料系统，（E-mail）suweidong@yapp.com

0 引 言

随着国民经济的增长，汽车的保有量越来越大，汽车轻量化是各个整车厂商和零部件供应商需要面对的问题。塑料燃油箱成型方案独特，对汽车底盘设计适应性高，逐渐成为主流趋势。普通塑料油箱仅约6～7 kg，既可减轻整车质量，还可降低制造成本，经济效益巨大[1-2]，所以塑料燃油箱的轻量化具有十分重要的意义。

塑料燃油箱壳体由高密度聚乙烯（high density polyethylene， HDPE）制成，采用可控制壁厚的挤出吹塑工艺。建立实际吹塑工艺的数学模型可以得到所需的模拟结果。[3-4]

1 塑料燃油箱数学模型

1.1 挤出吹塑型坯控制方案

傳统挤出吹塑可以采用垂直厚度分布系统、局部厚度分布系统、静态柔性变形板和口模滑移等方法优化型坯壁厚。两片式吹塑工艺的型坯分为2片，所以使用垂直厚度分布系统和静态柔性变形板方法优化型坯。垂直厚度分布系统和静态柔性变形板的模具几何结构和壁厚变化原理[5-6]见图1。

垂直厚度分布系统的口模开度随时间变化，主要控制型坯纬度方向的壁厚;静态柔性变形板主要用于成型非对称或方形容器，只控制型坯经度方向的壁厚。2种方式同时使用，可以对型坯中经纬交叉的任何位置进行壁厚控制。塑料燃油箱是异形体，油箱上面凸出的部位经过吹塑后壁厚会减薄，对应位置需要增加壁厚。如果调整纬度方向，那么同一纬度的各个位置都会相应地增加壁厚，使得总质量增加;如果调整经度方向，那么同一经度各个位置都相应地增加壁厚，也不经济。所以，如何既满足壁厚的要求，又同时使得油箱质量最小，是一个亟待解决的难题。[7]

建立实际工艺过程的数学模型并求解数学模型的最优值，是整个优化模型的关键。数学优化算法很多，如梯度优化法、直接搜索法、全局优化法和近似模型法等。[8]

梯度优化法的步骤是先确定初始点X0，然后按某一方向S0以初始步长a0寻找一个新点X1，使得函数值下降;重复这一过程，直至获得最优解，优化方程可写为

Xk+1 =Xk +ak Sk

（1）

式中：ak为步长;

Sk为搜索方向。计算Sk主要采用共轭梯度法，即

Sk+1 =-

Δ

f（xk+1 ）+

Δ

f（xk+1 ）2

Δ

f（xk ）2Sk

（2）

全局优化法主要解决目标函数的多峰性和非线性以及设计变量与约束函数的非线性和离散性等情况，主要包括多岛遗传算法、自适应模拟退火法和粒子群法等。

近似模型法是通过数学模型逼近一组输入变量与输出变量的方法，主要包括响应面法和神经网络法等。

根据挤出吹塑工艺特性，整个模拟过程相关数据不能完整地用方程式表示，因此将壁厚优化过程分为3个主要部分，即型坯长度优化、静态柔性变形板优化和垂直厚度分布系统优化，并建立相应的数学模型。[9-10]

1.2 型坯长度优化数学模型

型坯是由固态颗粒树脂经过加热、塑化后形成的高温黏流态物质。在吹塑工艺过程中，需要改变塑化树脂的量（简称塑化量）使得型坯长度满足吹塑工艺要求。考查各个工艺参数，得到塑化量与型坯长度成递增函数关系，即

y=f（x）

（3）

式中：y为型坯长度;x为塑化量。

定义目标函数为

G（x）=min y-y0

（4）

式中：y0为设定的目标长度。因此，长度优化问题即可转化为求解绝对值函数最小值的问题。

求解此类最小值问题有很多方法，比如下山法和全局搜索法等。由于函数y的表达式没有办法完全确定，所以采用二分法较为方便。设塑化量区间[a ， b]包含对应型坯长度的塑化量的值，将区间中点（a+b）/2代入式（3），可得到型坯长度;判断y-y0与0的 大小关系，如果y-y0>0，说明区间端点b需要减小，反之区间端点a需要增大：往复多次，直到满足y-y0≤ε。二分法相关理论和程序流程图分别见图2和3。

1.3 静态柔性变形板优化的数学模型

由于挤出吹塑工艺和产品壁厚要求的特殊性，需要对型坯经度方向的壁厚进行调整，目的是使各个经线方向的平均壁厚大致相等，其简化数学模型为

G（x）=min（std（var（T1，T2，T3，…，Tn）））

（5）

式中：std（ ）为标准差函数;var（ ）为变量列表函数;

Ti为第i经线方向的平均壁厚。

1.4 垂直厚度分布系统优化数学模型

垂直厚度分布系统控制型坯纬度方向的厚度，其简化数学模型为

G（x）=min ∑nj=1Wj

Tj-T0∞≤ε

（6）

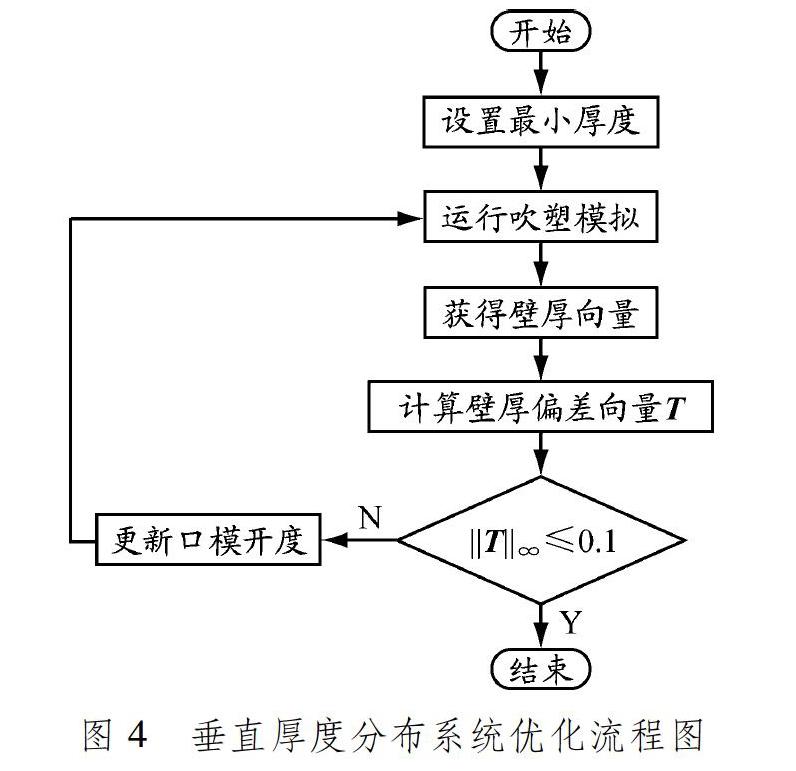
式中：Wj为第j个纬度方向的质量;Tj为第j纬度方向的最小厚度;T0为纬度方向设定的目标厚度。垂直厚度分布系统优化流程图见图4。

设定厚度与计算的最小厚度组成向量，求解向量差的无穷范数，使得范数小于规定的误差，直到程序结束。

2 优化模型与试验对比

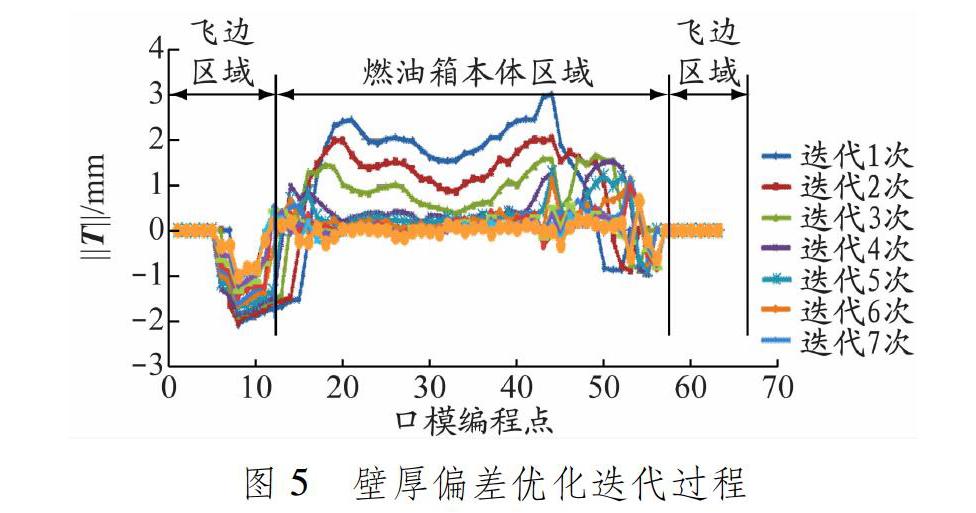
将上述数学模型转化为MATLAB程序，经过7～ 8次迭代后达到设定的结果。迭代过程见图5。

数值模拟结果与实际生产结果对比见图6。对比产品总质量，并从中拾取部分关键点的壁厚进行比较，模拟结果与实际生产结果的产品总质量偏差小于3%，局部壁厚度偏差不超过7%，说明模拟过程合理。

3 结束语

建立实际吹塑工艺的数学模型，借助MATLAB实现自动模拟，成功解决相关的技术问题，模拟结果与产品实际参数基本一致，说明模似方法合理，可作为产品优化的新手段。

参考文献：

[1]

桂欢欢， 桂娜， 刘剑. 塑料燃油箱在汽车上的应用及发展[J]. 工程塑料应用， 2010， 38（5）： 48-50. DOI： 10.3969/j.issn.1001-3539.2010.05.013.

[2]王乾. 燃油箱内置件焊装质量数字化检测技术与系统研究[D]. 上海： 上海交通大学， 2015： 1-21.

[3]周昊. 汽车塑料燃油箱的燃油渗透性研究[D]. 上海： 上海交通大学， 2014： 1-21.

[4]楊聪慧， 张德鹏. 汽车塑料燃油箱设计[J]. 汽车与驾驶维修（维修版）， 2017（12）： 135. DOI： 10.3969/j.issn.1004-2830.2017.12.085.

[5]黄虹， 李能文， 龙婷， 等. 基于吹胀压力参数优化中空工业制件壁厚均匀性的研究[J]. 塑料， 2011， 40（2）： 58-61.

[6]MU Y，ZHAO G Q， ANBIAO C. Modeling and simulation of polymer melts flow in extrusion process of plastic profile with metal insert[J]. International Journal of Advanced Manufacturing Technology， 2013， 67（1- 4）： 629-646. DOI： 10.1007/s00170-012-4511-7.

[7]王磊， 陈淮， 马晓建， 等. 非等温粘弹性熔体挤出成型过程的形态及性能[J]. 高分子材料科学与工程， 2014， 30（1）： 44- 47. DOI： 10.16865/j.cnki.1000-7555.2014.01.010.

[8]贾腾飞， 张洪信， 赵清海， 等. 基于Isight与Cruise耦合计算的汽车传动比优化[J]. 机械制造， 2017， 55（10）： 104-107. DOI： 10.3969/j.issn.1000- 4998.2017.10.030.

[9]王俊阳. MATLAB优化工具箱在机械优化设计中的应用[J]. 现代制造技术与装备， 2017（12）： 55.

[10]闫星辉， 郭迎清， 殷锴， 等. 基于MATLAB/Simulink的滑油系统建模仿真与优化[J]. 航空动力学报， 2017， 32（3）： 740-748. DOI： 10.13224/j.cnki.jasp.2017.03.028.

（编辑 武晓英）