160 km/h快捷货车隧道运行空气动力学特性数值分析

2019-12-20王东屏谢靖孙成龙赵亚军

计算机辅助工程 2019年4期

王东屏谢靖孙成龙赵亚军

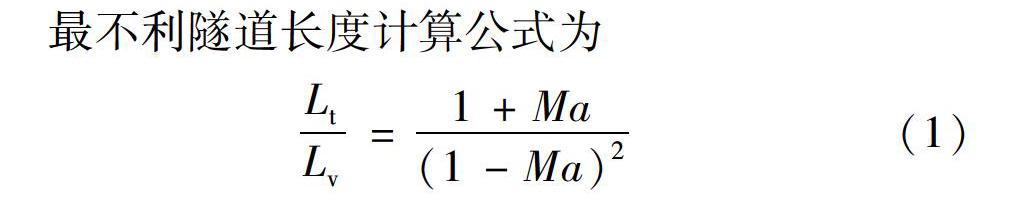
摘要：基于三维非定常可压缩N-S方程和k-ε两方程湍流模型，以4辆编组的新型快捷货运列车为研究对象，对快捷货车以160 km/h速度在200 m长的双线隧道运行全过程进行数值计算，结果表明：头车鼻端最高压力为明线运行时的122.67%;隧道壁面的最大正压出现在货车刚进入隧道时，约为366.32 Pa，最大负压出现在货车运行至隧道中部时，约为-329.65 Pa;货车穿越双线隧道时，以车体中心线所在的平面为对称面，车体两侧表面的压力分布不均衡，隧道侧壁近端的车体表面最大负压为远端的117.83%;货车以不同的速度运行时，头车鼻端、隧道壁面中点处最大压力与运行速度的平方成正比。

关键词：快捷货车; 隧道; 空气动力学; 表面压力; 数值计算

中图分类号：U260.171; TB115.1

文献标志码：B

收稿日期：2019-06-26

修回日期：2019-08-10

基金项目：

国家重点研发计划项目子任务（2017YFB1201302-11）

作者简介：

王东屏（1962—），女，陕西耀县人，教授，博士，研究方向为计算流体动力学工程应用，（E-mail）wdp@djtu.edu.cn

Aerodynamics characteristics numerical analysis of express

freight train passing through tunnel at 160 km/h

WANG Dongpinga， XIE Jingb， SUN Chenglonga， ZHAO Yajuna

（a.School of Mechanical Engineering; b.College of Locomotive and Rolling Stock Engineering，

Dalian Jiaotong University， Dalian 116028， Liaoning， China）

Abstract：

Based on the three-dimensional unsteady compressible N-S equation and k-ε two-equation turbulence model， by taking a new express freight train composed of four rolling stock as the research object， the numerical calculation of the whole moving process of the train running at 160 km/h in a 200-meterdouble-tracks tunnel is carried out. The results show that： the maximum pressure of leading vehicle nose is higher than that of open line operation by 122.67%; the maximum positive pressure on the tunnel wall occurs just at the truck entering the tunnel， which is about 366.32 Pa， and the maximum negative pressure occurs when the express truck runs to the middle of the tunnel， which is about -329.65Pa; when the train crossing double-tracks tunnel， the pressure distribution is asymmetric， and the maximum negative pressure on the train body surface near the tunnel side wallis higher thanthe far one by 117.83%; when the train runs at different velocities， the maximum pressure of leading vehicle nose and tunnel wall midpoint is directly proportional to the square of the train speed.

Key words：

express freight train; tunnel; aerodynamics; surface pressure; numerical calculation

0 引言

快捷貨车具有可使运输物品避免风吹雨淋、可承载多种包装货物、可运输货物范围广、通用性强和利用率高等优势，已被广泛应用到铁路货物运输中。[1]我国幅员辽阔，地势复杂，修建铁路不可避免会有隧道段，隧道更是被称为“绿色交通结构”。在众多已有铁路路线上，列车隧道运行已成为常态。[2]与明线运行相比，在隧道运行时，列车周围的流场急剧变化，空气动力特性更复杂。随着快捷货车运行速度的进一步提高，货车在隧道运行时产生的气动效应更明显，对车体外形和材料的要求也相应提高。[3]因此，有必要研究快捷货车在隧道运行时的空气动力学特性。

随着计算机的发展，计算流体动力学已成为研究流体的重要方法，数值分析方法也成为解决流体问题的重要手段。占俊[4]以CRH2型高速列车为研究对象，运用FLUENT模拟高速列车通过隧道时的气动效应，得到列车通过隧道时不同工况和时刻车体附近的流场压力云图和车体壁面空气压力散点连线图。陈晓丽[5]通过数值计算，以简化的CRH5型动车组为研究对象，对不同条件下列车驶出隧道过程的压力场、速度场和气动载荷进行数值分析，得到列车-隧道空气动力学特性变化规律。金琦[6]采用流场数值计算、动模型试验与风洞试验相结合的方法，研究集装箱平车在隧道运行的气动性能，得出车身测点的压力变化幅值和压力波特性。马东宝[7]以高速磁悬浮列车模型为研究对象，利用三维数值模拟方法研究磁悬浮列车通过隧道时的湍流外流场特性和气动力特性，建立列车-隧道数值模拟计算模型，验证磁悬浮列车通过隧道过程数值模拟计算结果的正确性。宋军浩等[8]采用动模型实验平台，在200～350 km/h速度范围内研究60 m双向隧道壁面压力波和出口微气压波，试验结果表明隧道压力波与出口微气压波的无量纲值保持一致，但难以确定隧道出口微气压波与流线型列车头型长度的定量关系。田红旗[9]通过数值模拟和风洞试验2种方法研究列车隧道运行，证明数值模拟是研究列车隧道运行的有效方法。王东屏等[10]建立都市快轨列车穿越矩形隧道的三维计算模型，应用不连续网格和动网格模拟快轨列车穿越隧道的动态过程，发现列车的气动阻力和车体表面压力变化幅值随着运行速度的增大而增大。目前，国内研究列车穿越隧道问题采用的车体大多是高速列车或者动车组，对货车穿越隧道时的空气动力学特性研究极少。随着快捷货车运行速度的提高，有必要研究其隧道空气动力学特性。

本文以最新研制的快捷货车为研究对象，数值计算其以160 km/h速度在隧道中运行的全过程，为新型快捷货车的设计和制造提供技术参考。

1 计算模型概述

1.1 算法原理

按照快捷货车的实际外形尺寸、隧道长度和隧道轮廓形状建立快捷货车和隧道流场计算模型并划分网格。在隧道中运行时，快捷货车周围空气流动为三维非定常可压缩流动，所以采用可压缩N-S方程和k-ε两方程湍流模型，对4辆编组的快捷货车隧道运行全过程进行数值计算，分析快捷货车穿越隧道时的空气动力学特性。

1.2 三维几何模型和网格划分

以最新研制的快捷货车为例，其三维几何模型非常复杂。为计算方便，对几何结构进行简化。车灯、受电弓、门把手等复杂结构对计算结果影响甚微，故去掉这些突出物。在隧道运行过程中，货车压力波主要受头车和尾车影响，故将快捷货车简化为1辆机车加3辆拖车的车体模型。简化后货车长、宽、高分别为104.63、3.10和3.93 m，快捷货车简化模型见图1。

货车进入隧道产生的压力波，会在隧道内部以接近声速的速度传播并产生剧烈波动，隧道过长会使压力波在隧道中过度衰减，隧道过短压力波不能完全作用在货车表面，所以隧道长度应由压力波的传播规律确定。

最不利隧道长度计算公式为

LtLv=1+Ma（1-Ma）2 （1）

式中：Lt为隧道长度，m;Lv为列车长度，m;Ma为马赫数。

由式（1）可计算得到该快捷列车的最不利隧道长度为187.52 m，因此为计算方便，取隧道长度为200.00 m。

采用单洞双线隧道形式，隧道形状根据《标准轨距铁路建筑限界》（GB 146.2—1983）确定，双线隧道净空面积为100 m2，线间距为5 m。[11]考虑快捷货车周围流场的充分发展，为保证本次数值计算结果精度，设列车明线运行流场的矩形长为360 m，宽为64 m，高为60 m，快捷货车初始位置为鼻端距隧道入口62 m，计算区域见图2。采用动网格模拟快捷货车隧道运行全过程。由于车体曲面较为复杂，车体表面和车体周围难以划分结构化网格，因此货车表面及其周围小部分区域采用四面体网格;隧道流场和明线流场尺寸较大且形状规则，采用六面体网格。快捷货车-隧道模型网格单元共约1 120万个。

2 计算结果分析

2.1 计算结果对比验证

为验证数值计算结果的可靠性，将数值计算结果与试验数值进行对比。采用新研制的160 km/h快捷货车车体模型，其隧道运行试验尚未开展，因此本文将计算结果与前人研究的列车隧道运行计算结果进行对比。现有列车隧道运行试验大多采用高速列车或者动车组，但快捷货车与高速列车车型不同，列车的空气动力学特性也不同，所以，将计算结果与车型相近的文献[6]中的快速集装箱平车气动性能进行对比。

本文采用的快捷货车为4辆车编组：头车+中车1+中车2+尾车。文献[6]试验采用的集装箱平车为3辆编组：头车+中车+尾车。每辆车体长度均相同。本文采用的隧道模型长度为200 m，文献[6]采用的隧道实际长度为888.88 m，其他计算参数基本一致。

2个模型隧道壁面压力变化曲线对比见图3。由此可知：货车开始进入隧道时，监测点处压力开始增大;当车头即将驶过该监测点时，监测点处压力升高至最大值;车头经过监测点后，监测点处压力急剧下降;车尾通过监测点时，监测点压力回升。由于本文采用的车体模型为4辆编组，文献[6]采用的车体模型为3辆编组，所以文献[6]中的列车车尾通过监测点的时间比本文早0.45 s，监测点压力回升提前0.45 s，但两者隧道壁面监测点的压力变化规律和幅值基本一致，说明本文数值计算合理。

2.2 快捷货车穿越双线隧道空气动力学特性分析

货车在明线稳态运行时，头车鼻端的理论压力为

P=12ρv2（2）

式中：P为货车头车鼻端的压力，Pa;ρ为空气密度，取1.225 kg/m3;v为货车的速度，m/s。

货车以160 km/h的速度在明线稳态运行时头车鼻端的理论压力为1 209.63 Pa。

快捷货车明线运行时的车体表面压力分布见图4。此时，头车鼻端压力最大值为1 175.84 Pa，中车1车体侧墙壁面压力约为-111.12 Pa。頭车鼻端压力值与理论值误差约为2%，说明本文的计算结果准确可靠。

头车鼻端驶入隧道35 m时快捷货车车体表面压力分布见图5。货车进入隧道1.4 s时，空气流动受到货车、隧道壁面和地面的约束，车体壁面和隧道壁面压力发生显著变化。头车前方的空气由于受到车体壁面、隧道壁面和隧道地面的挤压而急剧压缩，形成压缩波，头车鼻端处压力增大。货车运行2.3 s时，头车鼻端处压力升至最大值1 410.76 Pa，比明线运行时增大234.92 Pa;中车1车体侧墙压力上升至-99.62 Pa，比明线运行时增大11.50 Pa。

快捷货车刚驶入隧道时的隧道壁面压力分布见图6。隧道壁面压力逐层变化，快捷货车经过区域隧道壁面的压力分布不均匀。

尾车完全进入隧道时快捷货车的表面压力分布见图7。在货车不断驶入隧道的过程中，空气与隧道壁面、地面之间的摩擦阻力增大，减缓压缩波形成;同时尾车处负压形成膨胀波，膨胀波传播使得货车鼻端压力下降为1 098.92 Pa，比货车鼻端最大值减小约

311.84 Pa。货车头部产生的压缩波自隧道出口反射形成膨胀波，与货车尾部产生的膨胀波同时作用于中车1侧墙表面，车体表面压力开始急剧下降，中车1侧墙壁面压力约为-165.62 Pa，比货车驶入隧道35 m时减小约66.00 Pa。

快捷货车尾车完全进入隧道时的隧道壁面压力分布见图8。与货车刚进入隧道时相比，隧道壁面压力迅速降低;货车尾部完全进入隧道时，由于车体尾部负压产生的膨胀波在隧道内传播，使隧道壁面压力降低。

快捷货车运行至隧道中部时车体表面的压力分布见图9。货车运行至隧道中部时，头部被挤压的空气形成的压缩波传递至隧道出口后，以膨胀波的形式向隧道入口方向反射。尾车完全进入隧道后尾部压力突降产生膨胀波，该膨胀波向隧道出口方向传播。这2个相反方向的膨胀波共同作用，使头车鼻端和车体表面压力继续下降，此时鼻端的最大压力为1 032.94Pa，较货车刚驶入隧道时减小约377.82 Pa，中车1车体壁面压力达到最大负压，为-256.58 Pa，较货车刚驶入隧道时减小约 156.96 Pa。

货车运行至隧道中部时隧道表面压力分布见图10。压缩波传播使隧道壁面压力增加，膨胀波传播使隧道壁面压力减小。隧道壁面以负压为主，货车周围的隧道壁面压力比隧道进出口处的壁面压力低。

货车驶离隧道时车体表面压力分布见图11。此时货车前端的空气可以自由流动，头车鼻端、中车1车体侧墙壁面的压力开始上升，鼻端的最大压力为1 076.19Pa，车体壁面压力为-141.35Pa。

快捷货车驶离隧道时的隧道表面压力分布见图12。此时货车前端的空气可以自由流动，压力波的能量递减，同时，受隧道空气黏性作用和隧道壁面摩擦阻力的影响，隧道壁面压力减小，分布均匀。

2.3 监测点压力变化曲线

为直观准确地得到压力波动趋势，在货车头车鼻端、车身中部和隧道壁面定义监测点。由于模拟计算为单车过双线隧道，车体两侧与隧道壁面的距离不同，因此在车体两侧均设置监测点。

车体表面和隧道表面的压力监测点布置见图13。模拟计算选取11个监测点记录压力变化：监测点1位于头车鼻端中部，监测点2、4、6和8分别位于靠近隧道侧壁一侧的头车、中车1、中车2和尾车侧墙的中心处，监测点3、5、7和9分别位于远离隧道侧壁一侧的头车、中车1、中车2和尾车侧墙的中心处，监测点10和11分别位于靠近快捷货车侧距隧道入口20和100 m处的隧道表面上。

貨车头车鼻端监测点1的压力变化曲线见图14。

头车鼻端从1.4 s时开始进入隧道，5.9 s时驶离隧道。在1.4～5.9 s区间，由于隧道内压力波动复杂，鼻端压力波动明显。1.4 s货车鼻端进入隧道时，货车前方空气受到挤压，形成压缩波，头车鼻端压力增加，2.3 s时压力达到最大值1 410.76 Pa;快捷货车继续沿隧道前行，由于车尾处负压产生的膨胀波传递至头车鼻端，使鼻端压力下降;当产生的压缩波传递至隧道出口并以膨胀波的形式反射到头车鼻端后，鼻端压力继续下降，4.4 s时压力达到最小值1 015.16 Pa;此后膨胀波传递至隧道出口，以压缩波的形式向隧道入口方向反射，鼻端压力开始回升;5.0 s时，压缩波继续向隧道出口传播，到达隧道出口时又以膨胀波的方式向隧道入口方向传播至货车表面，鼻端压力下降;5.9 s时货车开始驶离隧道，此处

的空气压力

接近隧道出口处的大气压力，鼻端压力迅速回升至初始时刻的稳态压力值后保持基本不变。

中车1侧墙监测点压力变化见图15。靠近隧道壁面一侧的车体侧墙压力大于远离隧道壁面一侧的，靠近隧道壁面一侧的车体侧墙最大负压为-256.58 Pa，比远离隧道壁面一侧车体侧墙最大负压高45.23 Pa。在2.5 s时，货车头部压缩波自隧道出口反射回来形成膨胀波，与尾部产生的膨胀波共同作用于中车1侧墙表面，监测点处压力开始大幅下降;在3.5 s时，货车尾部产生的膨胀波传至隧道进口后，以压缩波的形式向隧道出口反射并传至货车表面，车体壁面压力开始上升;在3.9 s时，压缩波继续传播至隧道入口后又变为膨胀波传递至货车表面，车体壁面压力开始下降;在4.3 s时，货车尾部的膨胀波经入口反射后以压缩波的形式到达货车表面，车体壁面压力上升;在4.7 s时，货车头部的压缩波经隧道出口反射后，以膨胀波形式到达货车表面，车体壁面压力开始下降;在5.9 s后，货车逐渐驶出隧道，车体壁面压力又开始升高。由于压缩波和膨胀波每次反射都有一部分能量损失，所以总能量逐渐减小。

隧道壁面监测点的压力变化见图16。隧道壁面监测点10距隧道入口20 m，隧道壁面监测点11距隧道入口100 m。虽然隧道壁面监测点位置不同，但其压力变化趋势相似：当货车头部经过监测点时，该点压力迅速下降，当尾车通过该监测点时压力又迅速上升。监测点11压力变化比监测点10压力变化更大。

2.4 快捷货车以不同速度穿越双线隧道的空气动力学特性

当快捷货车以不同速度运行时，头车鼻端的压力对比见图17。货车鼻端压力曲线的波峰、波谷出现的时间不同，但是压力变化规律基本一致。头车鼻端最大正压均出现在货车刚进入隧道时，最大负压均出现在货车运行至隧道中部时。头车鼻端压力历经几次起伏变化，是压缩波和膨胀波在隧道内部来回传播和相互叠加作用影响的结果。

快捷货车以不同速度运行时头车鼻端压力极值对比曲线见图18。当同一速度运行时，头车鼻端压力曲线的波峰幅值比波谷幅值大;当列车以不同的速度运行时，隧道壁面压力波的峰值随速度的增大而增大，这说明当其他影响因素不变时，货车的运行速度越大，头车鼻端的压力越大，并且最大压力与最小压力的变化幅值也越大。

当快捷货车以不同速度运行时，隧道壁面监测点10压力变化曲线见图19。货车开始进入隧道时，监测点处压力开始变大;当车头即将驶过该监测点时，监测点处压力升高至最大值;车头经过监测点后，压力急剧下降;车尾通过监测点时，压力又上升。货车以不同的速度运行时，隧道壁面压力的最大值均出现在货车刚进入隧道时，最大负压均出现在货车运行至隧道中部时，虽然隧道壁面监测点曲线的波峰和波谷出现的时间不同，但是隧道壁面监测点的压力变化规律一致。

当快捷货车以不同速度运行时，隧道壁面监测点10的压力极值对比见图20。当快捷货车以同一速度运行时，隧道壁面压力曲线的波峰幅值比波谷幅值大;当货车以不同的速度运行时，隧道壁面压力波的波峰幅值和波谷幅值均随速度的增大而增大，说明当其他影响因素不变时，随着货车运行速度的增大，隧道内部压力波动越大，隧道表面压力变化幅值也越大。

为验证车速与车体表面、隧道壁面压力变化的关系，以货车鼻端和隧道壁面中点处监测点11的压力为例，计算得到不同车速时的压力变化最大幅值见表1。根据表1数据生成拟合曲线，分别得到鼻端和隧道壁面中点处压力幅值随速度变化的曲线，见图21。

头车鼻端、隧道壁面中点处压力与运行速度的拟合曲线的延长线均为通过原点的抛物线，头车鼻端监测点压力的拟合曲线幂指数为1.953 ，隧道壁面中点的压力拟合曲线幂指数为1.927 ，相关性因数均大于0.99。根据拟合关系式，头车鼻端和隧道壁面中点的最大压力变化值与运行速度的平方近似成正比，即头车鼻端的压力变化值满足ΔP=0.013 6v2，隧道壁面的压力变化值满足ΔP=0.020 7v2。这与文献[12]中的试验结果一致，证明本文数值计算结果准确。

3 结论

以我国最新研制的快捷货车为研究对象，对快捷货车双线隧道运行的全过程进行数值计算。在双线隧道长度为200 m的情况下，通过分析车体表面和隧道壁面压力分布规律，得出如下结论。

（1）快捷货车以160 km/h速度在隧道中运行时，货车鼻端进入隧道35 m处时鼻端压力升至最大值1 410.76 Pa，比明线运行时高

234.92 Pa;车体侧墙壁面的压力以负压为主，受到的最大压力波动与最大负压均出现在货车运行至隧道中部位置时;以车体中心线所在的平面为对称面，车体两侧表面的压力分布不均衡，隧道侧壁近端的车体表面最大负压比远端高45.23 Pa。

（2）隧道壁面的最大正压出现在货车刚进入隧道时，约为366.32 Pa;最大负压出现在货车运行至隧道中部时，约为-329.65 Pa。隧道中部壁面压力变化较大，隧道进、出口的壁面压力变化较小。

（3）快捷货车以不同速度在双线隧道行驶时，头车鼻端压力的幅值随车速的增大而增大。货车分别以100、120、140和160 km/h的速度穿越双线隧道时，头车鼻端的最大压力分别为602.91、839.11、1 138.94和1 410.62 Pa，最大压力变化与运行速度的平方成正比，比例因数为0.013 6，即ΔP=0.013 6 v2。

（4）快捷货车分别以100、120、140和160 km/h的速度穿越雙线隧道时，隧道壁面中点的最大压力分别为109.73、157.27、204.99和366.32 Pa，最大压力变化值与运行速度的平方成正比，比例因数为0.020 7，即ΔP=0.020 7v2。

参考文献：

[1]佟立本. 铁路概论[M]. 5版. 北京：中国铁道出版社， 2006： 1-30.

[2]杨新安，姚永勤，喻渝. 铁路隧道[M]. 北京：中国铁道出版社， 2011： 1-6.

[3]王磊，万晓艳，余南阳，等. 隧道单车压力波数值模拟验证研究[J]. 土木工程学报， 2006， 39（12）： 104-107.

[4]占俊. 高速列车气动效应的数值模拟和仿真研究[D]. 成都：西南交通大学， 2016.

[5]陈晓丽. 高速列车出隧道空气动力效应数值模拟研究[D]. 兰州：兰州交通大学， 2016.

[6]金琦. 160 km/h快速集装箱平车气动性能研究[D]. 长沙：中南大学， 2010. DOI： 10.7666/d.y1917025.

[7]马东宝. 时速600 km磁浮列车隧道压力波及气动力特性研究[D]. 兰州：兰州交通大学， 2018.

[8]宋军浩，郭迪龙，杨国伟，等. 高速列车隧道通过中的气动效应动模型实验研究[J]. 实验流体力学， 2017， 31（5）：

39- 45. DOI： 10.11729/syltlx20170002.

[9]田红旗. 中国列车空气动力学研究进展[J]. 交通运输工程学报， 2006， 6（1）： 1-9. DOI： 10.3321/j.issn：1671-1637.2006.01.001.