学习使我进步 创新使我快乐——记一个导数填空题的解决与拓广探究

李嘉杭 指导教师：许银伙 邹洪旺

(福建省泉州外国语学校高三8班 362000)

一、由一道填空题引发的思考

上学期期末复习时，老师在某个周末所分发的练习卷中有一个填空把关题, 让我百思不得其解，其问题是：设实数λ>0，若对任意的x∈(e2,+)，关于x的不等式λeλx-lnx≥0恒成立，则λ的最小值为____. 第二天上午，我请教许银伙老师，许老师对这个问题认真审阅，沉思良久，然后说：这个问题的解答探索，可以借鉴他所发表的两篇文章《投石问路，巧解难题》和《解压轴题之：特值代入，减少讨论》里所含的思路，回家先自行学习和探究下，下次再一起交流.回到家里，经过对文章的学习，我明白了对参数范围的探求，可以通过特殊值代入尝试，压缩讨论范围.在本题中，因为函数f(x)=λeλx-lnx的图象在定义域上是连续不断的，既然要对任意的x∈(e2,+)，关于x的不等式λeλx-lnx≥0恒成立，则首先必须有f(e2)≥0，也就是λeλe2-2≥0，此时λ的最小值怎么求出来呢？经过思考我看出式子λeλe2-2的值关于λ∈(0,+)单调递增，因此只要寻找到使λeλe2-2=0的λ值就可以了.因为λeλe2-2=0可化为观察得出它是所要求的结果吗？我尝试证明如下：

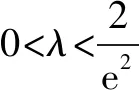
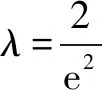
带着问题我拜访邹老师.邹老师详细看了问题解答，帮我分析说：从解题过程看，可以对条件x∈(e2,+)作一下改变，看看能不能构造出新题来或者总结一般性的规律来.

依照这个思路，如果把条件x∈(e2,+)改成x∈(e,+)或者x∈(e3,+)，情况会怎么样呢？

拓广问题1设实数λ>0，若对任意的x∈(e,+)，关于x的不等式λeλx-lnx≥0恒成立，则λ的最小值为____.

拓广问题2设实数λ>0，若对任意的x∈(e3,+)，关于x的不等式λeλx-lnx≥0恒成立，则λ的最小值为____.

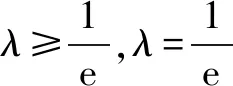
观察上面研究结果，我就想：由原来的问题是否可以归纳出一般性的结论呢？由此尝试得出下列两个问题.

拓广问题3设实数λ>0，k∈N*，若对任意的x∈(ek,+)，关于x的不等式λeλx-lnx≥0恒成立，则λ的最小值为____.

拓广问题4设实数λ>0，k≥1，若对任意的x∈(ek,+)，关于x的不等式λeλx-lnx≥0恒成立，则λ的最小值为____.

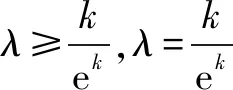
拓广问题5设实数λ>0，k≥1，a≥e，若对任意的x∈(ak,+)，关于x的不等式λaλx-logax≥0恒成立，则λ的最小值为____.

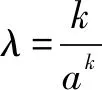
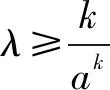
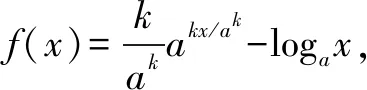
由以上解答过程看出，条件实数λ>0，k≥1，a≥e是个整体，似乎是不能改变的.果真不能变动吗？如果硬要变动，又应该有什么结论？在邹老师和许老师的协助下，我们又得出新的结论.

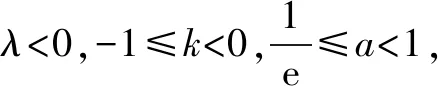
限于篇幅，证明过程略.

二、总结

一个练习题，我从无从下手，经过学习文章，悟出诀窍，然后在老师的指点下，得出一般性的结论，又继续扩展思路，把问题进一步改变，得出另外的结论.学习文章，请教老师，使我增加知识，打开思路；通过钻研和探究，我又获得创新性成果.通过这个事例，使我明白：学习是创新的基础，创新又促进学习，研究是学习与创新的桥梁.作为学生，作为新时代青年，我热爱学习，追求创新，对于学习和创新我永远在路上.