“失之交臂”的成功——几道错例剖析

龚发云

(甘肃省积石山县积石中学 731700)

一、忽视等价性变形致错举例

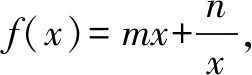
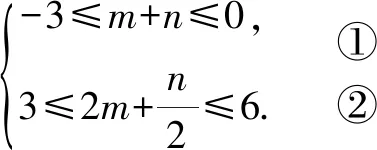
②×2-①,6≤m≤15,③

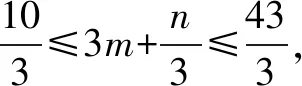
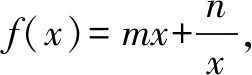
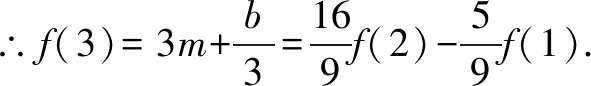
在本题正解中能把f(1)和f(2)的范围整体代入，避免了不等式转化中的不等价性，从而保证了解题的正确性.

二、忽视隐含条件致错举例

例2(1)设m、n方程x2-2kx+k+6=0的两个实根，则(m-1)2+(n-1)2的最小值是( ).

思路分析本例只有一个答案正确，设了3个陷阱，很容易被错误答案所迷惑.若利用一元二次方程根与系数的关系，易得：m+n=2k,mn=k+6,

∴(m-1)2+(n-1)2=m2-2m+1+n2-2n+1

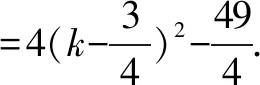
原方程有两个实根m、n，

∴Δ=4k2-4(k+6)≥0k≤-2或k≥3.

当k≥3时，(m-1)2+(n-1)2的最小值是8；

当k≤-2时，(m-1)2+(n-1)2的最小值是18. 显然只有B正确.

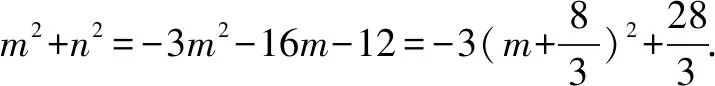
错误分析上述解法忽视了m的取值范围，所以导致了解法上的错误.

一般的隐含条件有：任何实数的偶次方非负，故x2≥0；三角函数中-1≤sinx≤1；指数函数ax>0;对数函数y=logax中(a>0且a≠1，且x>0)及圆锥曲线的有界性，三角形内角之和等于π等等，这些知识必须了然于胸,才会在解题中做到准确无误，游刃有余.

三、忽视基本不等式中等号成立的条件致错举例

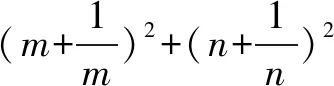
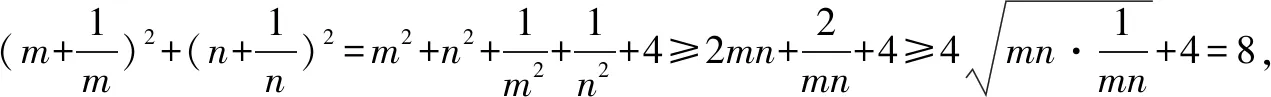
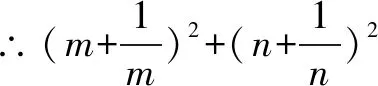
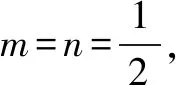
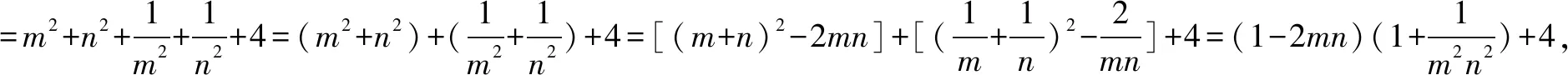
四、不注重细节致错举例

例4 已知数列{an}的前n项和Sn=2n+1，求an.

错误解法an=Sn-Sn-1=(2n+1)-(2n-1+1)=2n-2n-1=2n-1.

五、以偏概全致错举例

以偏概全是指思考不全面，以片面的情况，看待整体情况，而导致了解答不完整，是思维缺乏严谨准确性的具体表现.例如：

例5 设等比数列{an}的全n项和为Sn.若S3+S6=2S9，求数列的公比q.

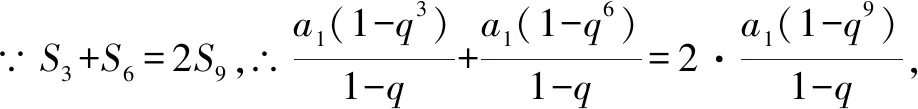
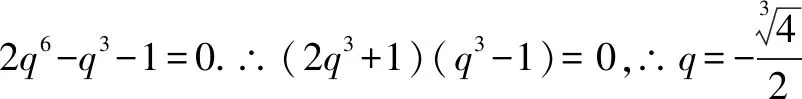
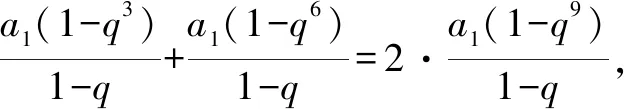
在等比数列中，a1≠0是显然的，但公比q完全可能为1，因此，在解题时应先讨论公比q=1的情况，再在q≠1的情况下，对式子进行整理变形.

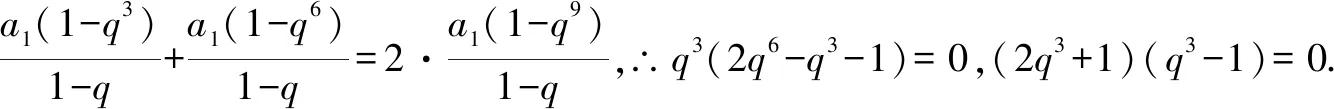
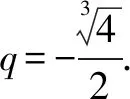
总之，要想在考试中不失分或少失分，就要针对以上情形加强平时训练，循序渐进，有的放矢，才会有备无患，才会在做题和考试中得心应手，满有把握.