强化求导后的“运算” 彰显数学核心素养

许国行

(江苏省板浦高级中学 222021)

一、直接求解型

例1求函数f(x)=x3-3x2-9x的单调区间.

解与析先令f′(x)=3x2-6x-9>0，即可直接解出该不等式的解：x<-1或x>3，所以函数的单调增区间为(-,-1)和(3,+)，减区间为(-1,3).

注此题在求导后, 解不等式f′(x)>0时, 直接利用一元二次不等式知识求解即可.

二、观察求解型

例2若对任意x∈(1,+), 不等式ex(x-1)-x-a>0都成立, 求实数a的取值范围.

解与析分参后得: ex(x-1)-x>a恒成立, 令f(x)=ex(x-1)-x, 即转化为求a0,即xex-1>0, 因为x>1, 所以ex>e,即xex>1×e=e,即不等式xex-1>0在x∈(1,+)内恒成立, 从而f′(x)>0在x∈(1,+)内恒成立, 所以f(x)在x∈(1,+)内单调递增, 即f(x)>f(1)=-1, 所以a≤-1.

此题在求导后, 解不等式f′(x)>0时, 此不等式xex-1>0不是常规的一元一次不等式或一元二次不等式, 不能够直接求解, 需要通过观察来帮助求解，重在观察的意识和观察的方向，可观察其范围和单调性来辅助求解不等式.

三、引值求解型

例3已知函数f(x)=ex-lnx，求证：f(x)>2.

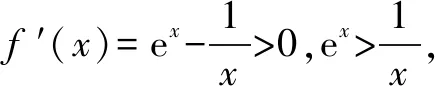
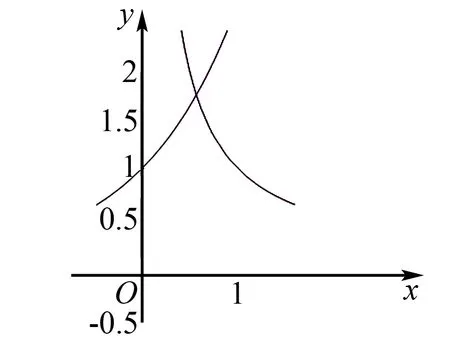
同理可得：x∈(x0,+)时,f′(x)>0，函数f(x)在(x0,+)上递增.故f(x)min=f(x0)=ex0-lnx0.

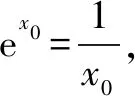
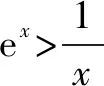
四、二次求导型

例4不等式ex-x2-m>0对任意的x∈(0,+)恒成立，求实数a的取值范围.

解与析分参后得: ex-x2>m恒成立, 即m<(ex-x2)min.设f(x)=ex-x2, 令f′(x)=ex-2x>0,再设h(x)=f′(x)=ex-2x, 令h′(x)=ex-2>0,得x>ln2,所以h(x)在(0,ln2)内递减,在(ln2,+)内递增, 即h(x)min=h(ln2)=eln2-2ln2=2-2ln2=2(1-ln2)>0,所以h(x)=f′(x)>0在x∈(0,+)恒成立, 从而f(x)在x∈(0,+)内为递增函数, 即f(x)>f(0)=1,所以a≤1.

注此题在求导后, 解不等式f′(x)=ex-2x>0时,观察法,或图像法都不能够顺利求解，只好选择二次求导,再研究h(x)=f′(x)=ex-2x的单调性,从而顺利证出f(x)在x∈(0,+)内为递增函数,即可求出最值.近年来,各省市的高考数学卷的中档及以下习题的分值, 约占百分之八十,每年阅卷老师都发现学生在数学运算方面失分较为严重, 制约了数学水平的提升,关于数学运算的素养问题,它还涉及学生的心理,运算的策略及运算的习惯等诸多因素,希望在平时的教学中老师和学生都能及时研究数学运算素养的提升.

五、问题的变式

变式已知函数f(x)=|x-a|+ex.

(1)若a=2,求函数f(x)的最小值;

(2)对任意的x∈(0,+),不等式f(x)≥4恒成立,求实数a的取值范围.

六、教学启示

1.运算能力未必是教出来的

解题是基本的数学学习形式之一,一位教师要面对多位思路活跃且思维有差异的学生,有些运算思路并不是教出来的,是学生自己根据经验和知识储备构建出来的,有时虽不完美或顺畅, 但其运算思路值得关注和借鉴,教师若只是一味地将成功的运算方法呈现给学生,让其模仿,显然是不够的,不同的学生,不同的想法,都有其合理性,完善和拓展其运算的思路或方向是老师的责任和义务,这有利于学生和老师自己的运算能力的提升.

2.给学生展示运算的机会

快节奏的多轮复习,是现在高三复习的特有现象,然而也忽略了给学生展示的机会,有些老师也就是能给学生展示思维方法的机会,很少能给学生自己运算的机会,认为方法有了,就能得分,这是片面的想法,每年的高考阅卷,都发现学生的运算能力才是决定高分的关键因素,因而我想提倡大家多给学生展示运算的机会,老师与学生交流的阵地在课堂,课堂中要舍得给学生时间去验算等,课下,组建学生学习研究小组,研究运算方法,总结运算的一些技巧等.

3.多激发学生思维，在比较中提升学生的运算能力

罗增儒教授在文献中指出：一个数学问题，如果我们只有一个解法，不管是自己想出来的还是翻答案看到的，都肯定会存在认识上的局限性.只有在得出两个或多个解法之后，才会对问题的实质有真正的了解，才能体会不同的思维所引起的不同运算方式，学生的运算能力在不同的思维中得以比较，提升学生对常规习题的运算能力.