等效思想在解题中的应用

张恒阳 指导教师：侯发展

(江苏省连云港市海州区高级中学高二1班 222000)

通过接近两年高中物理的学习发现，等效的思想方法几乎渗透于整个高中物理各个部分.例如合力和分力是等效的；合运动和分运动是等效的；合力的总功与动能的变化是等效的；合力的冲量与动量的变化是等效的；复杂的电路与一个简单的串并联电路可以是等效的；交变电流和直流电在一定程度上热效应是等效的.等效法是高中物理中处理物理问题的常用方法和重要方法，利用这种等效的方法可以快速的解决问题.下面举例谈一下等效思想在解题中的应用与小伙伴们分享.

一、合力与分力的等效性

合力和分力的作用效果是相同的，可以互相代替，有时候知道分力可以求出合力，有时候知道合力可以求出分力.

例题1如图1所示，用一根长1m的轻质细绳将一副质量为1kg的画框对称悬挂在墙壁上，已知绳能承受的最大张力为10N，为使绳不断裂，画框上两个挂钉的间距最大为( ).(g取10m/s2)

答案:A

小结这里两个绳子的拉力的合力可以等效为一个力，这个合力与重力平衡，大小相等，方向相反.知道合力与分力求分力之间的夹角.

二、运动过程可以等效

我们所研究物体的运动过程有时候是很复杂的，但是如果我们把过程与一个简单的过程等效起来，那么问题的处理起来就更简单.

例题2 如图2所示，一根长为l、质量为m的绳子搭在光滑的桌子上，绳子一半垂在桌面以下.在受到一扰动后从桌边下滑，则绳子离开桌边时的速度为____.

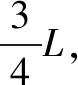
三、等效重力场

物体同时在受到重力的作用和电场力的作用，由于电场力和重力都是恒力，所以可以等效为一个力，电场和重力场等效为一个复合场.

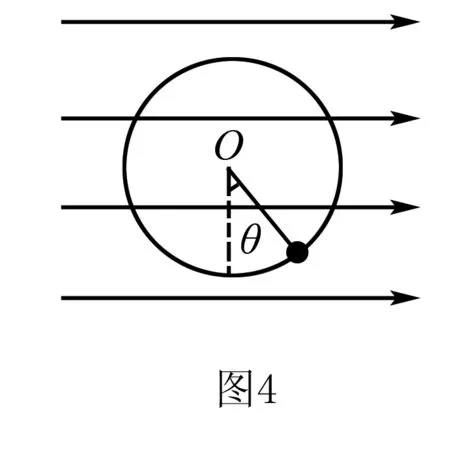
例题3 在水平方向的匀强电场中，有一质量为m的带正电的小球，用长为L的细线悬于O点，当小球平衡时，细线和竖直方向成θ角，如图4所示，现给小球一个冲量，冲量的方向和细线垂直，使小球恰能在竖直平面内做圆周运动.求：

(1)小球做圆周运动的过程中，在哪个位置有最小速度？并求这个速度值.

(2)施加的冲量值至少为多大？

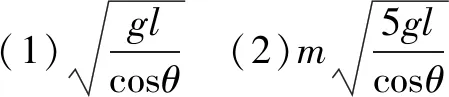
解析(1)由于重力和电场力都是恒力，则可以用它们的合力(即等效合外力)来代替重力，Q点就是等效最低点.分析其等效合外力对小球做功的情况，若等效合力做正功，则小球动能增大，反之小球动能减少.如图5所示小球受重力和电场力等效场力沿OQ方向，故小球运动到圆周上OQ反方向延长线上P点时，小球速度有最小值，就是等效最高点.

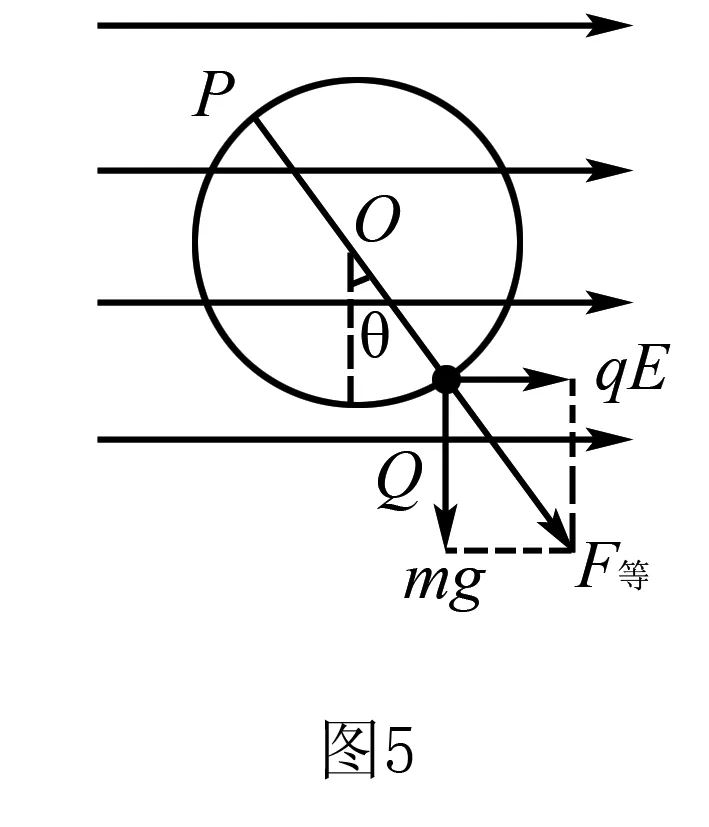
由图5可知，等效合外力

故最小速度值

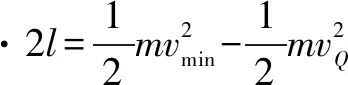
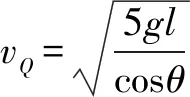
四、等效电源

电源的电动势反映电源把其他形式的能转化为电能的本领，它等于电源的内外电压之和，当电源的外电阻和内电阻相等时，电源的输出功率最大.有时候我们研究复杂电路时，把其中一部分电阻等效为电源内阻，处理问题非常简单.

例题4 如图6所示，R1=8Ω，电源的电动势E=8V，内阻r=2Ω，R2为变阻器，要使变阻器获得的电功率最大，R2的值应是多大？这时R2的功率多大？

答案：10Ω，1.6W.

解析把R1看成是电源内阻的一部分，这样内电阻(等效内阻)就是R1+r，利用电源输出功率最大的条件，可以求出：

当R2=R1+r=8+2=10Ω时，R2有最大功率

等效思想在高中物理中的应用还很多，利用等效法就是将所研究复杂问题通过适当的变换，化为简单的模型问题，将陌生的情景化为熟悉的情景等等，这样就能迅速、简捷找到解决问题的最佳途径，达到事半功倍之功效.本文例举一些等效的思维实例供小伙伴参考，我将继续总结研究高中物理中的重要思想方法.