证明函数不等式几种常用的策略

谢建宁

(福建省福州第十八中学 350001)

函数是高中数学的主干知识，与其他知识联系密切，是历年高考的必考内容.对函数不等式f(x)≥g(x)(或f(x)≥c)证明问题的考查，是近几年全国高考的热点，也是难点，常作为试卷的压轴题呈现，主要考查导数知识的应用，以及考查学生的逻辑推理、数学运算等核心素养. 笔者通过对近几年高考试题的研究，归纳出函数不等式证明的几种常用策略，希望能给读者带来帮助.

一、利用f(x)≥c等价于f(x)min≥c，f(x)≤c等价于f(x)max≤c进行转化

定理：f(x)≥c(c为常数)恒成立，等价于f(x)min≥c(或f(x)下确界≥c)；f(x)≤c(c为常数)恒成立，等价于f(x)max≤c(或f(x)上确界≤c).

利用此定理是证明函数不等式的基本策略，从而把问题转化为考察函数单调性、求最值的问题.

例1(2017全国Ⅲ卷(文)21)已知函数f(x)=lnx+ax2+(2a+1)x.

(1)讨论f(x)的单调性；

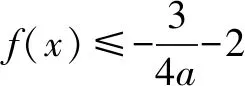
解析(1)当a≥0时，f(x)在(0,+)单调递增； 当a<0时，f(x)在单调递增，在)单调递减.(过程略)

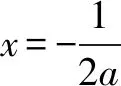
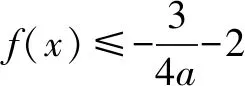
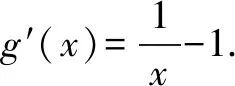
当x∈(0,1)时，g′(x)>0；当x∈(1,+)时，g′(x)<0.

所以g(x)在(0,1)上单调递增，在(1,+)上单调递减.

故当x=1时，g(x)取得最大值，最大值为g(1)=0.

所以当x>0时.g(x)≤0.

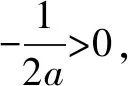
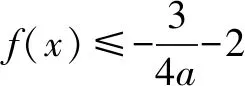
例2(2015课标全国Ⅰ卷(文)21)已知函数f(x)=ex-alnx.

(1)讨论f(x)的导函数f′(x)零点的个数；

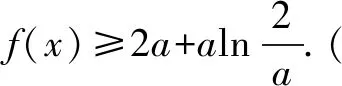
二、利用f(x)≥g(x)等价于(f(x)-g(x))min≥0或(f(x)-g(x))下确界≥0进行转化

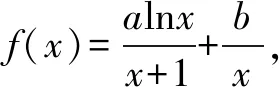
(1)求a,b的值；

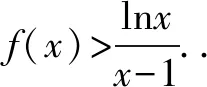
解析(1)a=1,b=1.(解题过程略)

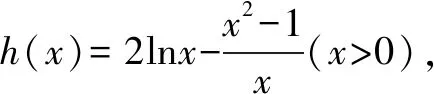
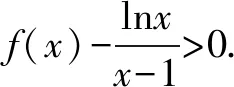
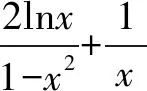
三、利用f(x)≥g(x)的充分条件f(x)min≥g(x)max进行转化

例4 证明：对任意的x∈(0,+)，都有成立.

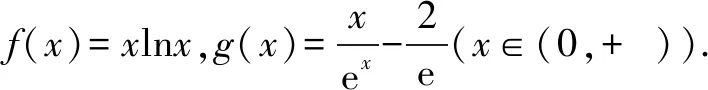
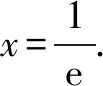
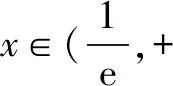
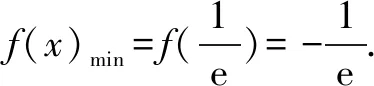
令g′(x)=0，得x=1；当x∈(0,1)时，g′(x)>0，g(x)单调递增；

当x∈(1,+)时，g′(x)<0，g(x)单调递减.

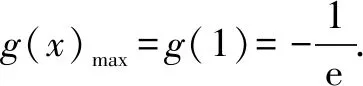
因此当x∈(0,+)时，恒成立.

又两次最值不能同时取到，所以对一切x∈(0,+)，都有

点评有时将不等式f(x)≥g(x)转化为证明f(x)-g(x)≥0，问题无法解决或计算复杂，可以尝试求解f(x)min与g(x)max，利用f(x)min≥g(x)max使问题得到解决.

四、利用f(x)≥g(x)的充分条件f(x)≥h(x)≥g(x)进行放缩

例5(2018全国Ⅰ卷(文)21)已知函数f(x)=aex-lnx-1.

(1)设x=2是f(x)极值点，求a，并求f(x)的单调区间；

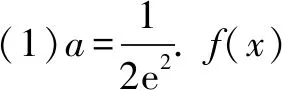
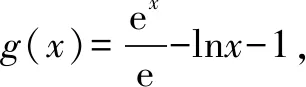
当x∈(0,1)时,g′(x)<0；当x∈(1,+)时.g′(x)>0.

所以x=1是g(x)的最小值点, 故当x>0时，g(x)≥g(1)=0.

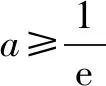
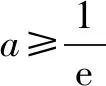
函数不等式的放缩常利用两曲线的公切线进行放缩，通过寻求两曲线的公切线，使两曲线分别落在公切线的上下方，从而证明不等式成立.

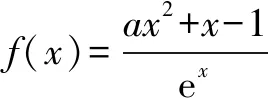
(1)求曲线y=f(x)在点(0,-1)处的切线方程.

(2)证明：当a≥1时，f(x)+e≥0.

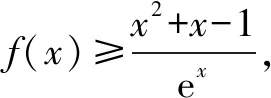
点评我们知道曲线y=ex在x=0处的切线方程是y=x+1，从而得到不等式ex≥x+1，以及由其变换可得ex+1≥x+2、e-x≥1-x等不等式，此题利用了直线y=x+2是曲线y=ex+1和y=-x2-x+1的公切线进行放缩.

五、先对所证不等式等价变形，再运用前四种策略证之

(1)求a,b；

(2)证明：f(x)>1.

解析(1)a=1,b=2.(过程略)

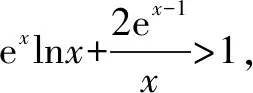
例8(2019厦门市高三一检)设函数f(x)=(x+1)ln(x+1)+ax2-x,a≥0.

(1)求f(x)的极值；

(2)证明：ex-1(f(x-1)+x)≥x2.

解析(1)f(x)的极小值为f(0)=0，无极大值.(过程略)

(2)要证ex-1(f(x-1)+x)≥x2,即证ex-1(xlnx+a(x-1)2+1)≥x2.

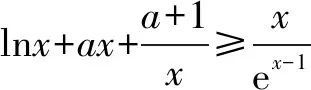
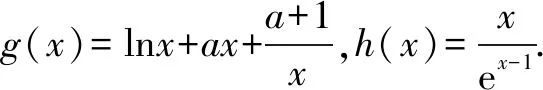
因为a≥0,x>0，所以当x∈(0,1)时，g′(x)<0，g(x)单调递减;

当x∈(1,+)时，g′(x)>0，g(x)单调递增.所以g(x)min=g(1)=2a+1.而所以当x∈(0,1)时，h′(x)>0，h(x)单调递增;当x∈(1,+)时，h′(x)<0，h(x)单调递减.所以，h(x)max=h(1)=1.

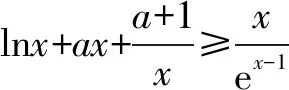
点评本题若直接构造差函数求最值，所得函数极其复杂，故先将不等式做等价变形，将对数函数与指数函数剥离开来，分离到等号两边，再运用策略三，分别求两边函数的最值，得到使不等式成立的充分条件，从而不等式得证.

对不等式的等价变形，要根据不等式的结构特点，可以通过移项、或作商、或两边取对数等手段，目的使所得不等式更易于证明.