Research on Time Synchronization Method Under Arbitrary Network Delay in Wireless Sensor Networks

Bing Hu,Feng Xiang,Fan Wu,Jian Liu,Zhe Sun and Zhixin Sun,

Abstract: To cope with the arbitrariness of the network delays,a novel method,referred to as the composite particle filter approach based on variational Bayesian (VB-CPF),is proposed herein to estimate the clock skew and clock offset in wireless sensor networks.VB-CPF is an improvement of the Gaussian mixture kalman particle filter (GMKPF) algorithm.In GMKPF,Expectation-Maximization (EM) algorithm needs to determine the number of mixture components in advance,and it is easy to generate overfitting and underfitting.Variational Bayesian EM (VB-EM) algorithm is introduced in this paper to determine the number of mixture components adaptively according to the observations.Moreover,to solve the problem of data packet loss caused by unreliable links,we propose a robust time synchronization (RTS) method in this paper.RTS establishes an autoregressive model for clock skew,and calculates the clock parameters based on the established autoregressive model in case of packet loss.The final simulation results illustrate that VB-CPF yields much more accurate results relative to GMKPF when the network delays are modeled in terms of an asymmetric Gaussian distribution.Moreover,RTS shows good robustness to the continuous and random dropout of time messages.

Keywords: Time synchronization,particle filter,expectation maximization,wireless sensor networks (WSNs).

1 Introduction

Wireless sensor networks (WSNs) consist of many low-cost sensor nodes capable of onboard sensing,computing and communications.WSNs are gaining importance since its wide applications,such as environment monitoring,object tracking and industrial machines controlling,etc.Most of these applications require the time of nodes to be synchronized to each other.Furthermore,some fundamental operations,such as power management,data fusion and transmission scheduling,etc.Require all the nodes running on a common timescale.However,in WSNs,every individual sensor works independently and maintains a local time measured by its own clock.This makes time synchronization between different nodes a critical piece of infrastructure [Wang,Jiang,Zhou et al.(2017);Qiu,Zhang,Qiao et al.(2018);Liu (2018);Chen,Liu and Han (2018)].

Usually,time synchronization between any two nodes is accomplished through the exchange of time messages.Since deterministic and nondeterministic delay exists in the process of message transmission,the time messages may be arbitrarily delayed.At present,the common solution is to build a distribution model for the nondeterministic network delay,such as,Gaussian,Exponent,Gamma and Weber etc.[Wu,Chaudhari and Serpedin (2011);Wang,Jeske and Serpedin (2015);Noh,Chaudhari and Serpedin (2007)].However,for sensor networks with complex real environment,various reasons will affect the distribution of network delay in varying degrees.It is difficult to find a network delay distribution model that is in line with the actual environment.Although the rationality and applicability of Gaussian network delay distribution model and Exponential network delay distribution model are verified in reference [Etzlinger,Wymeersch and Springer (2013);Abdel-Ghaffar (2002)],the simulation results in Noh et al.[Noh,Chaudhari and Serpedin (2007)] show that the estimation accuracy of clock parameters is very sensitive to the network delay distribution model.Therefore,it is necessary to research the clock parameter estimation method under arbitrary delay [Kim,Lee,Serpedin et al.(2009);Kim,Lee,Serpedin et al.(2011);Guo,Shen,Sun et al.(2015)].

Since Gaussian Mixture Model (GMM) can approximate arbitrary probability density [Anderson and Moore (1979)],Kim et al.[Kim,Lee,Serpedin et al.(2009)] estimated nondeterministic delay distribution using GMM,and proposed two estimation algorithms of clock offset,Gaussian Mixture Kalman Particle Filter (GMKPF),and Iterative Gaussian Mixture Kalman Particle Filter (IGMKPF),respectively.GMKPF combines measurement update steps based on Important Sampling (IS) with Gaussian Sum Filter (GSF) based on Kalman Filter (KF) for time update and proposed distribution generation.Then,Expectation Maximization (EM) algorithm is used to approximate the posterior distribution function of clock parameters by GMM.The introduction of EM algorithm not only alleviates the particle degradation problem caused by the particle filer algorithm,but also avoids the phenomenon that the number of GMM components increases exponentially with the iterations number increases.The simulation results of GMKPF show that when the network delay follows a single non-Gaussian (non-Exponential) distribution or a mixture of arbitrary distributions,it can maintain high synchronization accuracy with fewer message exchanges.However,GMKPF only tracks the clock offset and dose not estimate the clock skew,which will greatly reduce the synchronization period and increase communication overhead.Moreover,when GMKPF uses EM algorithm to approximate posterior distribution function with GMM,it needs to determine the components number of GMM beforehand,which is prone to under-fitting or over-fitting,and the estimation accuracy of parameters depends on the initial values setting.If set improperly,it is likely to converge to the local maximum.On the other hand,the unreliability of sensor network links may lead to the loss of time messages during transmission,while GMKPF does not discuss the algorithm performance in this case.

Therefore,we propose a Composite Particle Filter Approach based on Variational Bayesian (VB-CPF) to realize the joint estimation of clock offset and skew in this paper.

VB-CPF replaces the EM algorithm with Variational Bayesian EM (VB-EM) algorithm,which is used to estimate the GMM parameters of posterior distribution function.VB-EM algorithm is a deterministic approximate reasoning algorithm.It can determine the number of mixture components while determining the estimated values of mixture model parameters.Moreover,in order to solve the problem of time message loss caused by unreliable links,a robust time synchronization method (RTS) is proposed.RTS establishes an autoregressive model for clock skew,and utilizes the estimated clock skew obtained from each iteration of VB-CPF to estimate the autoregressive model parameters by recursive least squares method.If the time message is not received,the node can estimate the current clock parameters through the established clock skew autoregressive model,thus improving the robustness of the time synchronization method.

2 System model

2.1 Discrete clock model

The clock model of sensor node A is shown in Formula (1).

where βAand θArepresents the clock rate and initial clock phase,respectively.Since βAis time-varying,the above model can be expressed as an integral form,as shown in formula (2).

Time synchronization between nodes is usually achieved by the exchange of time stamps,which can be regarded as disc rete samples of continuous time.Assuming that the sampling period is τ0,the discrete clock model of node A is

where vA(n) denotes the cumulative clock offset,βA(k) denotes the instantaneous clock skew at the k-th sampling.According to the analysis of Luo [Luo (2014)],the timevarying clock skew βA(n) can be described by the Gauss-Markov model,that is

On the other hand,according to the definition of cumulative clock offset in formula (3),the recursive form of vA(n) can be written as

Substituting formula (4) into formula (5),and obtain

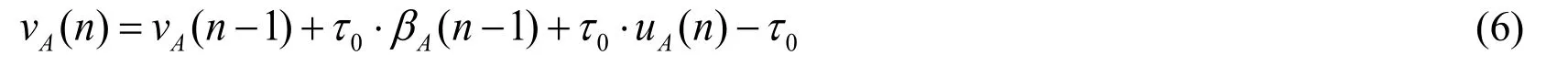
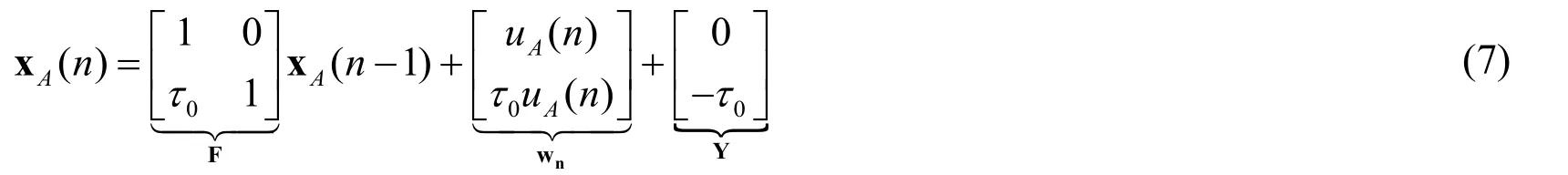
2.2 Local timestamp measurement model

In order to establish the clock relationship between two neighbor nodes,a two-way timestamps exchange mechanism is adopted in this paper.As shown in Fig.1,in the ithround of message exchange,R sends a synchronization message to A at ti1,embedding its clock reading.Upon reception of this message at ti2,A records its time,and replies R at.The replied message contains both time-stampsand.Then R records the reception time of A's replay as.Note thatandare clock readings recorded by R,whileandare recorded by A.After N rounds of message exchange,the node R obtains a set of time stampsThe above procedure can be modeled as

where d represents the deterministic delay in message transmission between two nodes,Xiand Yirepresent the nondeterministic delays.

Figure 1:Two-way time-stamps exchange between two nodes R and A

For the time to complete a round of message exchange is very short,we assume that the clock parameters remain unchanged during a round of message exchange.Firstly,the clock model (2) is represented by reference clock and accumulative clock,as follows:

To simplify symbolic representation ， letthen formulas (8) and (9) can be simplified as

Add formula (11) and formula (12),and let,then,a discrete local time measurement model is obtained by sampling,as shown in formula (13).

where zA(n) is the observed value,H =[0 2]Tis the observation vector,Vnis the observation noise.It is easy to observe that formulas (7) and (13) transform the estimation of clock parameters into Gauss-Markov estimation with unknown states.

3 VB-CPF

3.1 KF based time update and proposed distribution generation

Firstly,it should be noted that all probability density function can be approximated by the GMM shown in formula (14) [Anderson and Moore (1979)].

where G is the number of mixture components in GMM,φ(g)represents the mixture weights and satisfiesdenotes a normal distribution with µ(g)mean and variance Σ(g).

To simplify symbolic representation，letSuppose that at time 1n-,the posterior probability density functionand the density function of observed noise1nV-are approximated by the following GMMs.

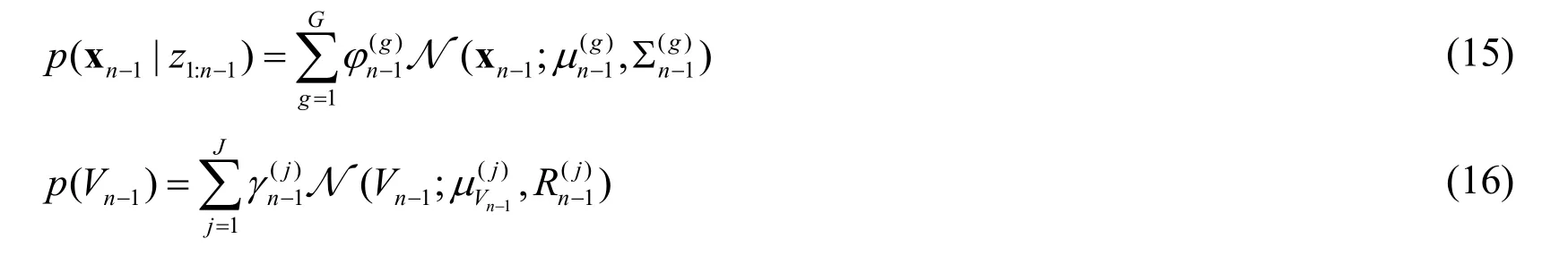
It can be known from formula (4),nu is a Gaussian noise with zero mean and variance σu2,so the state noise in formula (7) obey,then

At time n,the distribution of the current state can be predicted based on previous observations and state information,that is

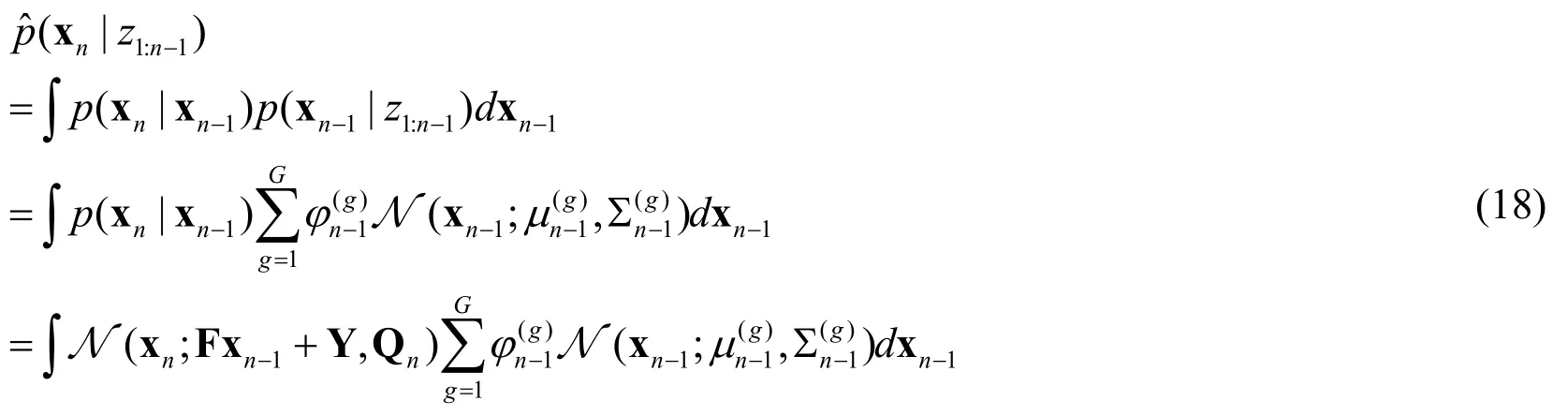
Theorem 1[Anderson and Moore (1979)] If the state equation of the system is the form of xn=fn(xn-1)+gn(xn-1)wn-1,and p(xn-1|z1:n-1) can be expressed in form of Gauss sum as shown in formula (15),then the one-step predictive density function is uniformly close to Gauss sum

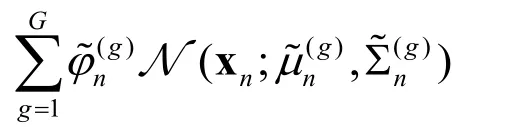
The mixture model parameters can be obtained from a set of parallel KF.

Then,according to the latest observation value znobtained from the system observation Eq.(13),combined with the density functions p (xn-1|z1:n-1) and p (Vn),the measurement update of the posterior density function(xn| z1:n) is completed by KF.The measurement update process of(xn| z1:n) is shown in formula (21).

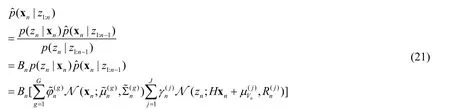
Theorem 2[Anderson and Moore (1979)] If the observation equation of the system is the form of zn=hn(xn)+Vn,and p (xn|z1:n-1) can be expressed in form of Gauss sum as shown in formula (19),then the updated posterior density function(xn| z1:n) is uniformly close to Gauss sum

So have

where

Then update its weight

3.2 Measurement update based on VB-EM algorithm

IS is a Monte Carlo method,which represents distribution p（x）by empirical approximation based on weighted particle (sample) set,that is,where δ（·） is a Dirac delta function and the weighted particle setis obtained from the proposed distribution q(x) .The first step in implementing IS is to sample particles from the proposed distribution function(formula (22)),and then calculate their corresponding importance weights.

Normalized importance weights

Then the posterior probability density p (xn| z1:n) can be approximated as

However,after many iterations,the weights of most particles are negligible,and only a few particles have large weights,thus resulting in the phenomenon of particle weight degradation.Although the introduction of resampling step alleviates the problem of particle degradation to a certain extent [Gordon,Salmond and Smith (1993)],excessive resampling will lead to particle depletion.Therefore,VB-EM algorithm is used to replace the resampling step to avoid particle depletion.Here,the GMM expression for posterior probability density p(xn| z1:n) is

where G denotes the number of mixture components in GMMs,denotes the weight of each mixture component,is a normal distribution withmean and covariance matrix.The Gaussian mixture is specified by the parameter setIn order to facilitate the calculation of VBEM algorithm,the precision matrixis used to replace the covariance matrix,in which the precision matrix is the inverse of the covariance matrix.

According to the above description,particle setare sampled from the proposed distribution.Hidden variablesare introduced,whereindicates which Gaussian distribution is the particlecoming from and satisfiesUnder given mixture weightthe conditional probability density of the hidden variables is [Ishikawa,Takeuchi and Nakano (2010)]

Under the condition of given hidden variables and model parameters,the conditional probability density of particle set Xnis [Bishop (2016)]

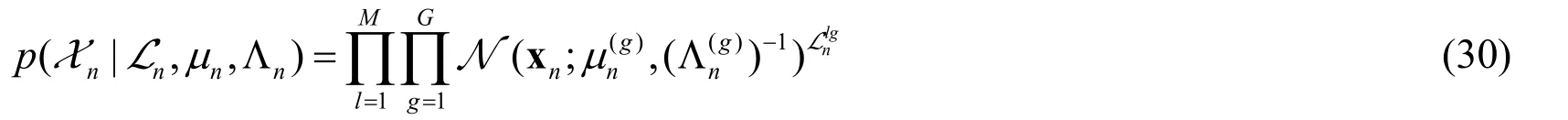
Since the Bayesian estimation is used to solve the GMM parameters,all parameters in the model are considered as random variables.Assume that the prior distribution of the mixture weight φnobeys the Dirichlet distribution [Gorur and Rasmussen (2010)].

The prior distribution of mean µnand precision matrix Λnobeys the joint Gaussian-Wishart distribution [Bishop (2016)].

where ϑ0,m0,ℓ0,ℜ0,℘0are all parameters to be sought,and subscript 0 indicates the initialization value.The goal of solving the GMM parameters using the Bayesian method is to calculate the posterior distribution p (Ln,φn,µn,Λn| Xn) based on the a priori information described above,but it is difficult to directly calculate the posterior distribution with high dimension.Therefore,VB-EM introduces approximate distribution q (Ln,φn,µn,Λn),and gradually approximates to the real posterior distribution through continuous iterative updating.First,the marginal likelihood function ln p (Xn) is analyzed.

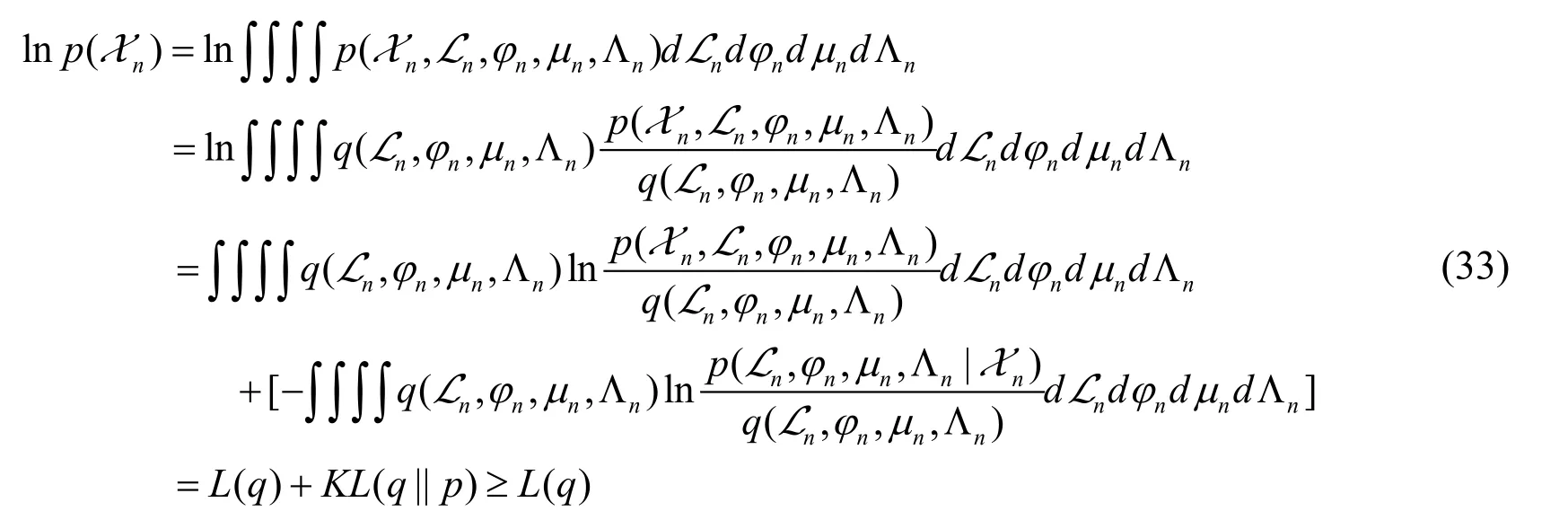
where

KL (q || p) is the KL (Kullback-Leibler) divergence of the approximate distribution and the true posterior distribution,and KL (q || p) ≥ 0,so L (q) is a lower bound of ln p (Xn),also called the lower bound of variation.When the approximate distribution q (Ln,φn,µn,Λn) reaches to the real posterior distribution p(Ln,φn,µn,Λn| Xn),that is q(Ln,φn,µn,Λn)=p(Ln,φn,µn,Λn| Xn),then KL (q || p)=0.Since ln p (Xn) is fixed by the distribution q (Ln,φn,µn,Λn),if you want to minimize KL (q || p),you only need to maximize L (q).

The distribution q(Ln,φn,µn,Λn) can be decomposed into the following form [Bishop (2016)]

VB-EM algorithm is a generalized EM algorithm,which is also an iterative algorithm.There are also two iterative steps,namely VB-E step and VB-M step.

VB-E:Bring the decomposition form of formula (37) into formula (35),and obtain

Then find the partial derivative of L (p) in respect to q (Ln),and let it equal to 0,after calculation

where const is a constant independent of variables,

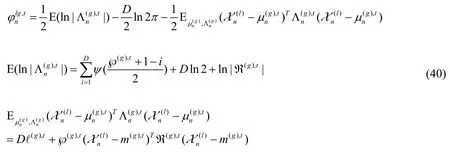
D denotes the dimension of the unknown state,()ψ ·is the digamma function.Take exponent on both sides of formula (39),then normalized

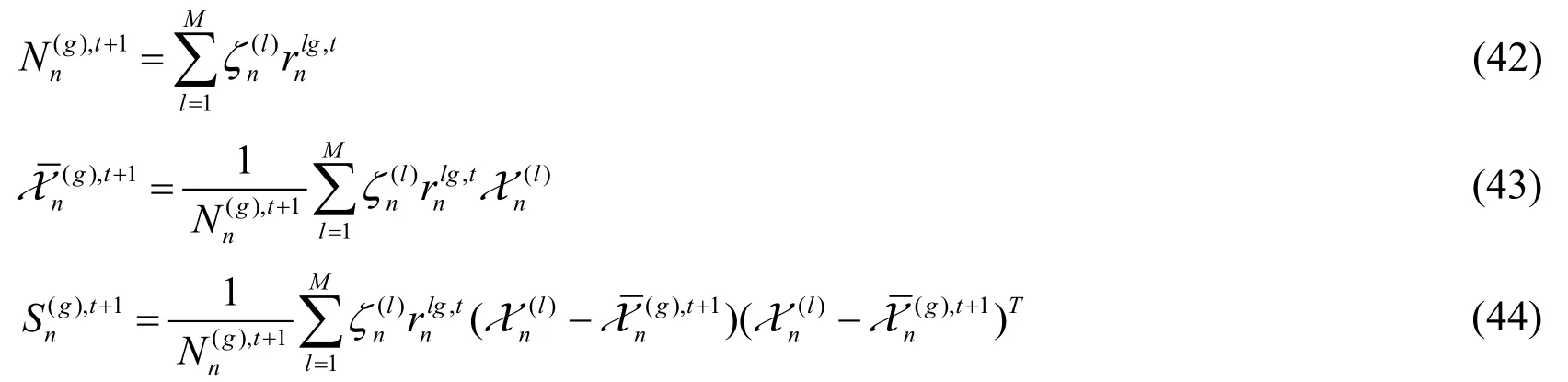
VB-M:Calculateaccording to formula (38),and let it equal to 0,after calculation

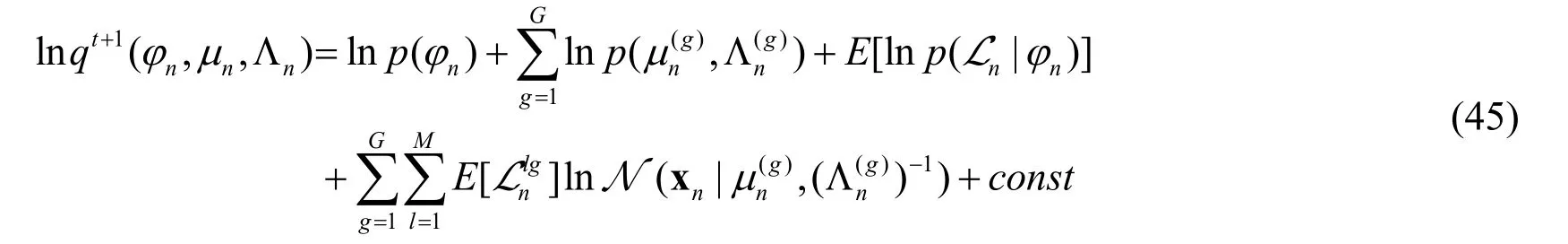
Similarly,take exponent on both sides of formula (46),and obtain

For qt+1(µn,Λn),we know that it obeys the Gaussian-Wishart distribution,that is

where

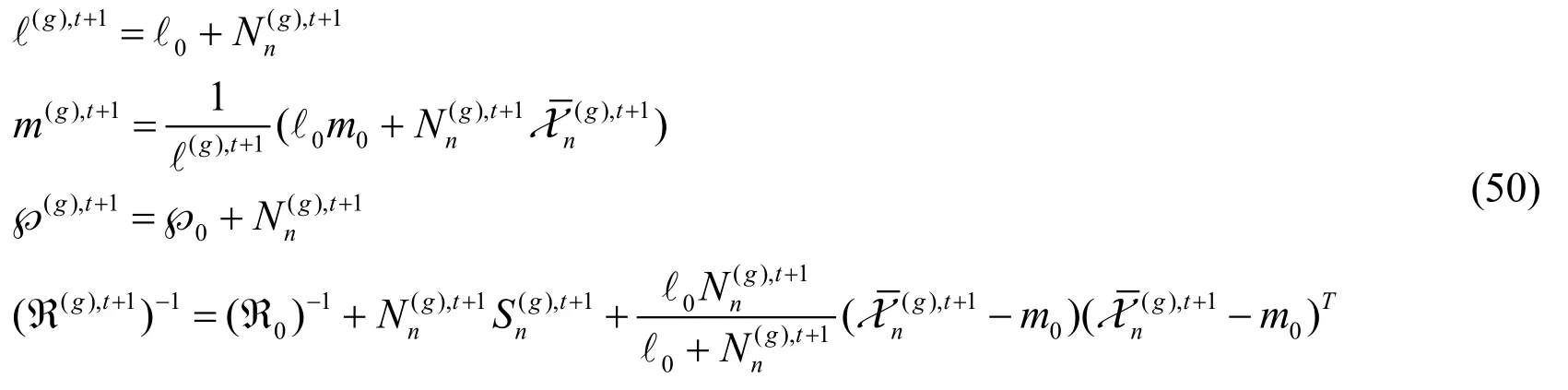
Therefore,the weight,mean and variances of the gthGaussian mixture component arerespectively,where E () can be obtained from the properties of Wishart distribution.

VB-E and VB-M are executed alternately and iteratively.As the number of iterations increases,L (q) gradually increases.The iteration is performed until | Lt+1(q) - Lt(q)|＜ εwhere ε is the predetermined error limit.

Finally,the conditional meanand the corresponding error covariancecan be obtained in two ways.The first one is obtained directly from the weighted sum of the particle set of formula (27) before the VB-EM algorithm is executed.

The second is calculated according to the formula (28) by using the weighted particle set fitted by GMM.

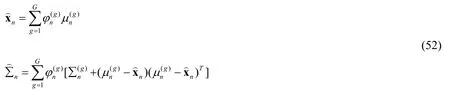
The estimation performance of formula (51) is better than that of formula (52).However,because of M ≫ G,the first kind of computation complexity is higher than the second one.The pseudo code of VB-CPF is as follows.

Composite Particle Filter Approach based on Variational Bayesian (VB-CPF) Initialization 1) The probability density function expression of the initial state 0x is () () ()0 0 0 0 0() (;,) G g g g g=1 pφµ=Σ∑x x N 2) Assume that at 1(1)n n- ＞,the forms of the posterior density function,process noise and observed noise density function are as follows ·posterior density function () () ()1 1:1 1 1 1 1 1(|) (;,) G g g g n n n n n n g pzφ µ- - - - - -==Σ∑x x N·process noise density function () (;,)n n n p =w w 0 Q N ·observed noise density function () () ()1() (;,)n J j j j n n n V n j=p V V R γ µ=∑ N Prediction process 1) time update A set of parallel KF is used to calculate the one-step predictive density function 1:1 ˆ(|)n n p z -x,and the update formula of the parameter is shown in (20).2) measurement update (the generation of proposed distribution) A set of parallel KF is used to calculate the posterior density function 1:ˆ(|)n n p zx,and the update formulas of the parameter are shown in (23) and (24).Measurement update process 1) Sampling M particles ( ){ ;1,,}l n l M χ=… from the proposed distribution function 1:() (|)n n n q p z=ˆ x x 2) Initialization,assign initial values to 0ϑ,0m,0ℓ,0ℜ,0℘ and error limits ε

3) Calculate ,lg t nr according to formula (40),then calculate the formulas (42)-(44) 4) Update the parameters in formula (50) with the calculation result in step 3),and then calculate 1()tL q+ 5) If 1| () ()|t t L q L q ε+ - ≥,go back to step 3).Otherwise,stop iterating and get the optimal parameter estimation ( ), 1 ( ), 1 ( ), 1 ( ), 1 ( ), 1,,,,g t g t g t g t g t m ϑ+++++℘ ℜℓ,where 1,2,,g G= … State estimation Estimate system state and variance using formulas (51) and (52).

4 Robust time synchronization method (RTS)

In practical sensor networks,the links between nodes are unreliable and susceptible to external interference,so the packets containing timestamps may be lost or collided during transmission.In order to solve the problem of data packet loss,the traditional wireless network can solve it by simply retransmitting.However,data packet retransmitting is infeasible for WSNs,because the energy cost of data retransmitting is too large,and the uncertainty delay in the process of data packet retransmitting will also affect the accuracy of time synchronization.So how to ensure the estimation accuracy of clock parameters in the case of data packet loss is the problem to be solved in this section.

According to Section 2.1,βA(n) varies with time in the actual environment,and for each sampling,it is not completely independent [Kim (2014);Kim,Ma and Hamilton (2012)].Moreover,due to the insufficient energy of nodes and the change of temperature,it may change greatly.In this section,the time-varying clock skew is modeled as an Auto-Regressive (AR) process [Tibshirani (2011)],and then the parameters of AR model are estimated by recursive least square method based on the estimated clock skew obtained by VB-CPF.When encountering data packet loss,the clock parameters of the next time can be estimated according to the AR model,which ensures the robustness of VB-CPF method in unreliable link environment.The AR model of clock skew is as follows.

where P is the order of AR model,πl(l=1,2,...,P) is AR coefficient,η (n) is Gauss noise with zero mean and variance ση2.This section chooses P= 4,i.e.,because the fourth-order autoregressive model can simulate the time-varying characteristics of clock skew very well,and its computational complexity is not very high [Kim (2014)].Next,the process of solving AR coefficients is described.

Assuming that the first five transmitted time messages are received correctly,according to the above estimation method,we can obtain five estimation values of clock skew,i.e.,(β1,β2,β3,β4,β5),where βn=xn[1],xn[1] represents the first element of column vector xn.Then

According to the recursive least squares estimation method,the mean square error matrix of π1is calcul ated first.

Then we can obtain the estimated value of1π

When β6is obtained,the AR coeffici ents are updated in the following recursive form according to the M1andcalculated for the first time.

Step 1:calculate the mean square error matrix of π2,

Step 2:update AR coefficient,where

Each time a new clock skew estimated value is obtained,AR coefficients are updated according to the above process.With the number of updates increase,AR model fits the estimated value of clock skew better.When the time message is lost or destroyed during transmission,the node can estimate the current clock skew according to the AR model.The overall method block diagram of RTS is shown in Fig.2.

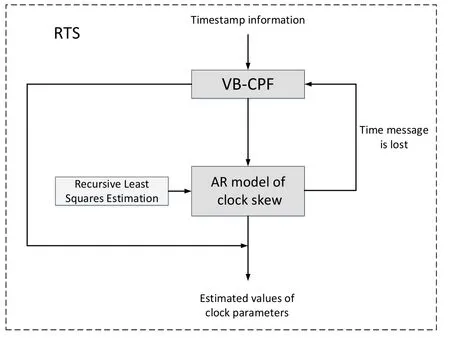
Figure 2:The overall method block diagram of RTS

5 Simulation experiment

To validate the performances of the proposed algorithm,simulation results are presented and compared to GMKPF.Since the VB-CPF method proposed in this paper is an improvement to GMKPF,in order to simplify the description of the simulation results,this section only evaluates the performance of the VB-CPF method under the asymmetric Gaussian delay model,in which the variance of the uplink nondeterministic Gaussian del ay is σ1=0.5,and the downlink is σ2=1.And the other parameters used in simulations are as follows.Initial clock offsets,clock offsets and deterministic delays are uniformly drawn from ranges [ -5 τ05τ0],[0.9 1.1] and [0.01τ00.02τ0],respectively,where τ0=0.1s .The variance of uAin formula (4) is= 10-4.The number of the mixture components in GMM is 3.The performance of the algorithm is evaluated using the mean square error of the clock parameter estimated value.

where S is the number of times the simulation experiment is executed,let 100S=.The smaller the value of MSE,the higher the estimation accuracy of the clock parameters.

Firstly,the effects of time message exchange times N (number of observations) and particle number M on the performance of VB-CPF are analyzed.As shown in Fig.3 and Fig.4,as the number of time message exchanges increases,the MSE of the clock parameter estimate gradually decreases,and when 20N ＞,the magnitude of the MSE decrease become smaller.It can also be seen that when the number of particles is large (M ≥ 400),the value of MSE is smaller.Obviously,through 5 times message exchanges,the estimated value of clock parameters obtained by sampling 500 particles per time is less than that obtained by 25 times message exchanges and sampling 100 particles per time.Therefore,the number of message exchanges can be reduced by increasing the number of particles sampled,thus reducing the communication overhead.

As shown in Fig.5 and Fig.6,when the number of time message exchanges is fixed,the MSE of the estimated clock parameters decreases with the increase of the number of particles.When the number of particles is greater than 600,the MSE of the cumulative clock offset estimates decreases slightly.When the number of particles is greater than 500,the MSE of the clock skew estimates tends to be stable.Therefore,considering the synchronization accuracy and computational complexity,in the following comparative analysis of the performance of VB-CPF and GMKPF,we select the number of particles M=500.

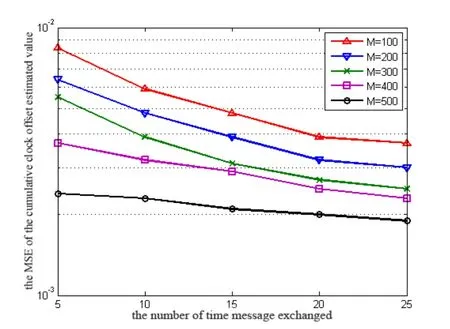
Figure 3:The relationship the MSE of the cumulative clock offset estimated value and the number of time message exchanged

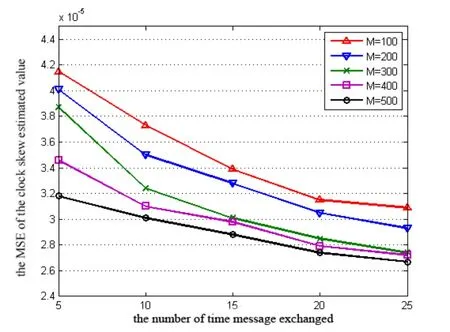
Figure 4:The relationship the MSE of the clock skew estimated value and the number of time message exchanged

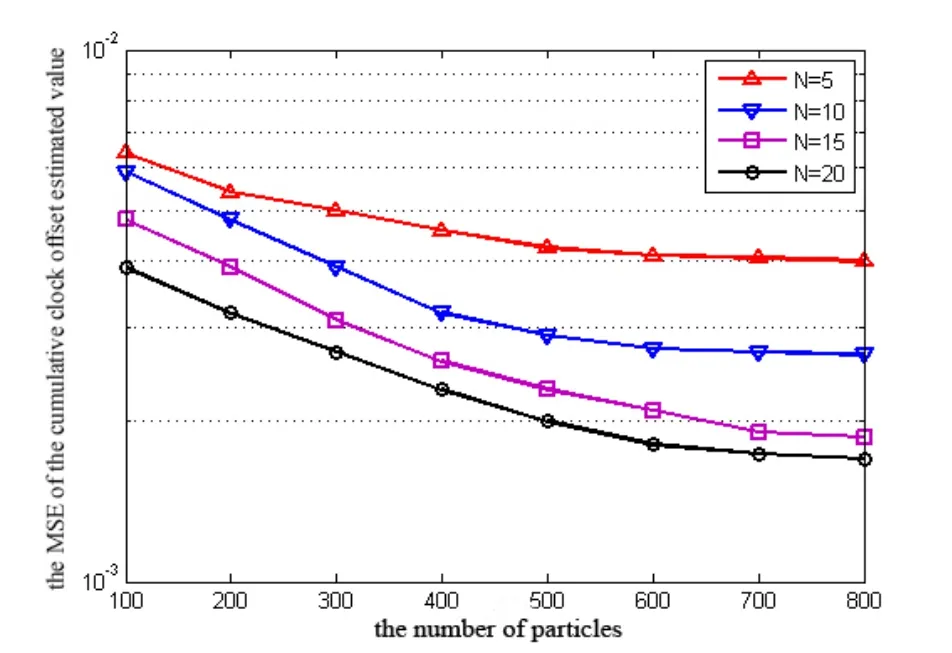
Figure 5:The relationship the MSE of the cumulative clock offset estimated value and the number of particles

Figure 6:The relationship the MSE of the clock skew estimated value and the number of particles

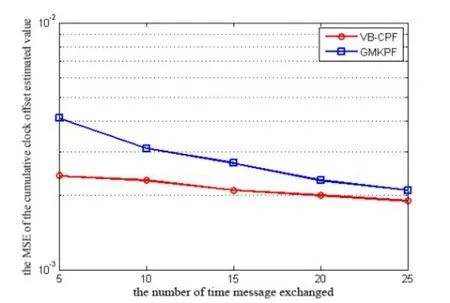
Figure 7:The MSE of the cumulative clock offset estimated value

Figure 8:The MSE of the clock skew estimated value

The time synchronization method proposed in Serpedin et al.[Serpedin,Kim and Lee (2009);Kim,Lee,Serpedin et al.(2011)] uses GMKPF algorithm to estimate the clock offset,while the simulation results shown in Fig.7 and Fig.8 are the joint estimated value of cumulative clock offset and clock skew,which is obtained using the GMKPF algorithm.As can be seen from the figure,the MSE of the clock parameters estimated value decreases gradually with the increase of the number of time message exchanges.Comparing the two hybrid filtering methods:VB-CPF and GMKPF,the performance of VB-CPF is better than that of GMKPF.This is because VB-CPF uses VB-EM algorithm for Gaussian mixture fitting of sampled particles.VB-EM algorithm can adaptively determine the number of mixture components,avoiding the problem of over-fitting and under-fitting caused by the EM algorithm to determine the number of mixture components in advance.

Next,we evaluate the performance of VB-CPF and RTS in the case of time message lost.The simulation experiments consider two types of time message dropout:(1) continuous dropout,(2) random dropout.Fig.9 shows the performance comparison of VB-CPF and RTS when time messages (observations) are lost five times in a row.Obviously,the performance of RTS is only 10-6difference from the estimation result without message dropout,which is better than that of VB-CPF.This is because,in each time of message loss,RTS estimates the cumulative clock offset and clock skew based on the preestablished clock skew model,while VB-CPF cannot update the estimated clock parameters.However,as the number of message loss increases,the MSE of the clock parameter estimate by RTS gradually increases.This is because the autoregressive model established for the clock skew is a statistical prediction model that predicts future values based on past estimated clock skew values.Therefore,when the time message is lost for a long time,the performance of the RTS will not be guaranteed.

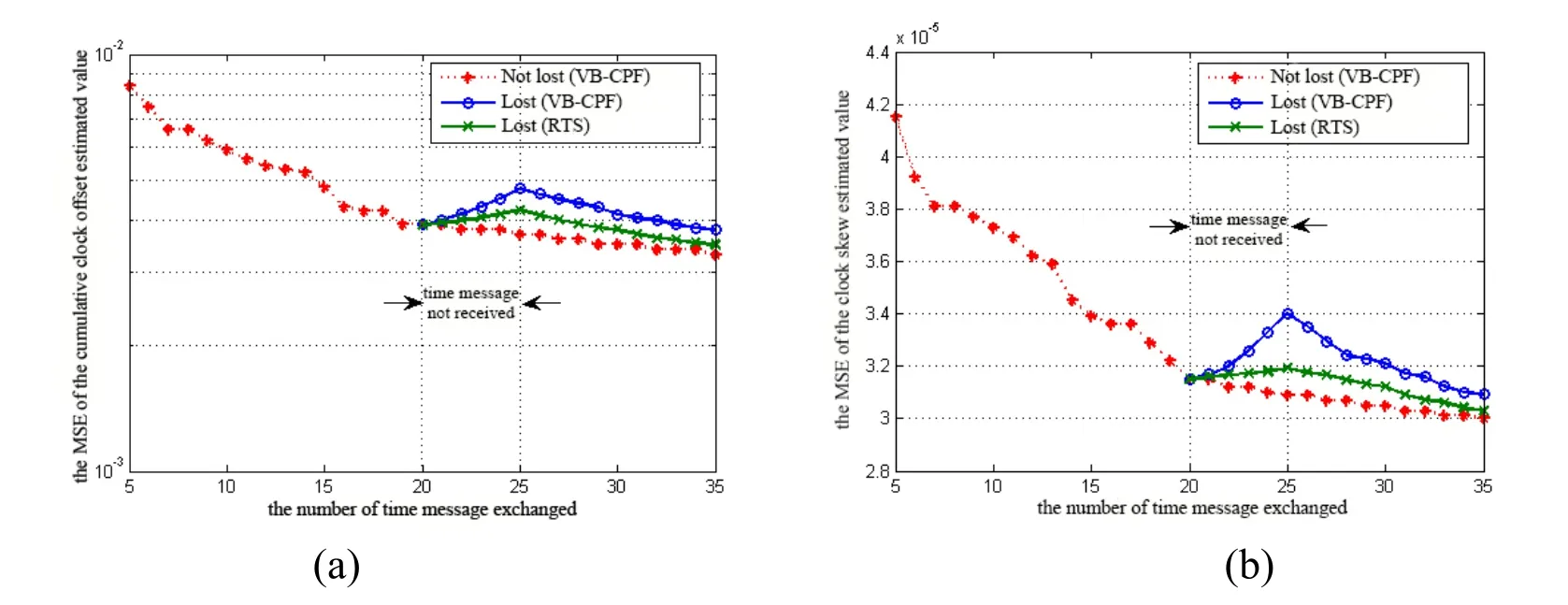
Figure 9:When time messages are lost continuously,the MSE of (a) the cumulative clock offset estimated value and (b) the clock skew estimated value

When time messages are lost randomly,Fig.10 shows the performance comparison of VB-CPF and RTS.When encountering message loss,the estimation performance of cumulative clock offset that used VB-CPF decrease 5.26 × 1 0-4on average when compared with the case of no messages loss,while the estimation performance of RTS decrease 2.54 × 1 0-4on average.Similarly,the estimation performance of clock skew that used VB-CPF decrease 1.62 × 1 0-6on average when compared with the case of no messages loss,while the estimation performance of RTS only decrease 6.39 × 1 0-7on average.Obviously,the MSE of the clock parameter estimation obtained by RTS is smaller than that of VB-CPF,so the robustness of RTS in dealing with time message loss is better than that of VB-CPF.According to the analysis of Fig.9 and Fig.10,RTS can show better performance regardless of whether the time messages are continuous dropout or random dropout.This shows that RTS can well solve the problem of synchronization accuracy decline caused by the time message dropout.

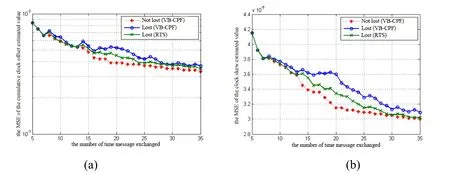
Figure 10:When time messages are lost randomly,the MSE of (a) the cumulative clock offset estimated value and (b) the clock skew estimated value

6 Conclusions

A composite particle filter approach based on variational Bayesian (VB-CPF) is proposed in this paper.VB-CPF replaces the EM algorithm used by GMKPF in estimating the parameters of Gaussian mixture model of the posterior distribution function of clock parameters with VB-EM algorithm,which makes it possible to determine the number of mixture components adaptively,thereby improving the estimation accuracy of clock parameters.At the same time,in order to solve the problem of time message dropout caused by unreliable link,a robust time synchronization method (RTS) is designed.RTS improves the robustness of VB-CPF in unstable network environment by establishing an autoregressive model for clock skew.The simulation results show that the estimation accuracy of clock parameters obtained by VB-CPF is better than that obtained by GMKPF,and RTS is robust to the continuous and random dropout of time messages.

Acknowledgement:This work was supported by the National Natural Science Foundation of China (No.61672299),the Natural Science Foundation of the Higher Education Institutions of Jiangsu Province of China (No.18KJB520035),the Youth Foundation of Nanjing University of Finance and Economics (No.L-JXL18002),the Youth Foundation of Nanjing University of Posts and Telecommunications (No.NY218142) and the Natural Science Foundation of Jiangsu Province (No.BK20160913).The authors would like to thank anonymous reviewers for their valuable suggestions.

References

Abdel-Ghaffar,H.S.(2002):Analysis of synchronization algorithms with time-out control over networks with exponentially symmetric delays.IEEE Transactions on Communications,vol.50,no.10,pp.1652-1661.

Anderson,B.D.O.;Moore,J.B.(1979):Optimal Filtering.Englewood Cliffs,NJ:Prentice-Hall.

Bishop,C.M.(2016):Pattern Recognition and Machine Learning.Springer.

Chen,H.P.;Liu,K.X.;Han,Y.(2018):A novel time-aware frame adjustment strategy for RFID anti-collision.Computers,Materials ＆ Continua,vol.57,no.2,pp.195-204.

Etzlinger,B.;Wymeersch,H.;Springer,A.(2013):Cooperative synchronization in wireless networks.IEEE Transactions on Signal Processing,vol.62,no.11,pp.2837-2849.

Gordon,N.J.;Salmond,D.J.;Smith,A.F.M.(1993):Novel approach to nonlinear/non-Gaussian Bayesian state estimation.IEEE Proceedings-F Radar and Signal Processing,vol.140,no.2,pp.107-113.

Gorur,D.;Rasmussen,C.E.(2010):Dirichlet process gaussian mixture models:choice of the base distribution.Journal of Computer Science and Technology,vol.25,no.4,pp.653-664.

Guo,C.S.;Shen,J.;Sun,Y.;Ying,N.(2015):RB particle filter time synchronization algorithm based on the DPM model.Sensors,vol.15,no.9,pp.22249-22265.

Ishikawa,Y.;Takeuchi,I.;Nakano,R.(2010):Multi-directional search from the primitive initial point for Gaussian mixture estimation using variational Bayes method.Neural Networks,vol.23,no.3,pp.356-364.

Kim,H.Y.(2014):Modeling and Tracking Time-Varying Clock Drifts in Wireless Networks (Ph.D.Thesis).Georgia Institute of Technology.

Kim,H.;Ma,X.L.;Hamilton,B.R.(2012):Tracking low-precision clocks with timevarying drifts using kalman filtering.IEEE/ACM Transactions on Networking,vol.20,no.1,pp.257-270.

Kim,J.S.;Lee,J.;Serpedin,E.;Qaraqe,K.(2009):A robust estimation scheme for clock phase offsets in wireless sensor networks in the presence of non-Gaussian random delays.Signal Processing,vol.89,no.6,pp.1155-1161.

Kim,J.S.;Lee,J.;Serpedin,E.;Qaraqe,K.(2011):Robust clock synchronization in wireless sensor networks through noise density estimation.IEEE Transactions on Signal Processing,vol.59,no.7,pp.3035-3047.

Liu,X.D.;Liu,Q.(2018):A dual-spline approach to load error repair in a HEMS sensor network.Computers,Materials ＆ Continua,vol.57,no.2,pp.179-194.

Luo,B.(2014):Distributed Clock Synchronization for Wireless Sensor Networks (Ph.D.Thesis).HongKong University.

Noh,K.L.;Chaudhari,Q.M.;Serpedin,E.;Suter,B.W.(2007):Novel clock phase offset and skew estimation using two-way timing message exchanges for wireless sensor networks.IEEE Transactions on Communications,vol.55,no.4,pp.766-777.

Qiu,T.;Zhang,Y.S.;Qiao,D.J.;Zhang,X.Y.;Wymore,M.L.et al.(2018):A robust time synchronization scheme for industrial internet of things.IEEE Transactions on Industrial Informatics,vol.14,no.8,pp.3570-3580.

Tibshirani,R.(2011):Regression shrinkage and selection via the lasso:a retrospective.Journal of the Royal Statistical Society B-Statistical Methodology,vol.73,no.3,pp.273-282.

Wang,W.D.;Jiang,S.F.;Zhou,H.F.;Yang,M.;Ni,Y.Q.et al.(2018):Time synchronization for acceleration measurement data of Jiangyin bridge subjected to a ship collision.Structural Control ＆ Health Monitoring,vol.25,no.1,e2039.

Wang,X.;Jeske,D.;Serpedin,E.(2015):An overview of a class of clock synchronization algorithms for wireless sensor networks:a statistical signal processing perspective.Algorithms,vol.8,no.3,pp.590-620.

Wu,Y.C.;Chaudhari,Q.;Serpedin,E.(2011):Clock synchronization of wireless sensor networks.IEEE Signal Processing Magazine,vol.28,no.1,pp.124-138.