SVM Model Selection Using PSO for Learning Handwritten Arabic Characters

Mamouni El Mamoun ,Zennaki Mahmoud and Sadouni Kaddour

Abstract: Using Support Vector Machine (SVM) requires the selection of several parameters such as multi-class strategy type (one-against-all or one-against-one),the regularization parameter C,kernel function and their parameters.The choice of these parameters has a great influence on the performance of the final classifier.This paper considers the grid search method and the particle swarm optimization (PSO) technique that have allowed to quickly select and scan a large space of SVM parameters.A comparative study of the SVM models is also presented to examine the convergence speed and the results of each model.SVM is applied to handwritten Arabic characters learning,with a database containing 4840 Arabic characters in their different positions (isolated,beginning,middle and end).Some very promising results have been achieved.

Keywords: SVM,PSO,handwritten Arabic,grid search,character recognition.

1 Introduction

Research on Arabic characters recognition reveals a rapidly expanding field and is now a concern whose relevance is undisputed by the research community,which has devoted its efforts to reducing constraints and expanding the field of Arabic character recognition.

Among the techniques used for Arabic handwriting recognition is the SVM introduced in the early 1990s by Boser et al.[Boser,Guyon and Vapnik (1992);Cortes and Vapnik (1995)],which has been very successful in many areas of machine learning.Today,it can be said without exaggeration that these machines have replaced neural networks and other learning techniques.

The adjustment of the hyper-parameters of the SVM classifier is a crucial step in building an effective recognition system.For a long time,the model selection was carried out by a “grid search” method,where a systematic search is implemented by discretizing the parameter space using a fixed step [Xiao,Ren,Lei et al.(2014);Wojciech,Sabina and Andrzej (2015)].More recently,model selection has been considered as an optimization task.In this context,an optimization algorithm is implemented in order to find all the hyperparameters that achieve the best classification performance.Among the existing optimization algorithms,the gradient descent method has often been used for SVM model selection [Ayat,Cheriet and Suen (2005);Jiang and Siddiqui (2019)].

Metaheuristic techniques were also used for SVM model selection.Genetic algorithms [Sun,Guo,Wang et al.(2017);Phan,Nguyen and Bui (2017)],evolutionary strategies [Liu,Liu,Yang et al.(2006);Phienthrakul and Kijsirikul (2010)] and taboo search metaheuristic [Zennaki,Mamouni and Sadouni (2013);Corazza,Di Martino,Ferrucci et al.(2013)] were used to find the best configuration of SVM parameters.

In this work,the PSO technique was adapted for parameter selection in order to maximize the cross validation accuracy and a comparative study between different SVM models is presented.

The rest of the article is organized as follows.Section 2 presents the SVM and the two multiclass approaches one-against-all and one-against-one.The PSO method is described in Section 3.Section 4 provides a brief description of the proposed recognition system.Section 5 describes the experimental results.Finally,Section 6 draws the conclusions of this study.

2 Support vector machine

Originally,SVM processes the binary classification (two classes).Considering the learning base S composed of input vectors xi,the classification of these vectors is known in advance.It is represented by the output vector:yi={-1,1}.It is therefore sufficient to know the sign of the classifier to determine the class of the example.If S is of dimensionm,then the output value of binary classifier is given by:

and ∀(xi,yi)∈S,0 ≤αi≤C et ∑iyiαi=0

where,Kis the kernel function,C the coefficient of regularization and αithe coefficients of Lagrange.

The learning algorithm for SVM aims to find the hyperplane of maximum geometric margin that separates the data in variables space as shown in Fig.1.Vapnik [Vapnik (1998)] was the first to introduce hyperplane concepts into support vector algorithms.

Figure 1:Representation of the hyperplane separating the data in the variables space

To determine the hyperplane equation,the problem is modeled as a mathematical program that maximizes the geometric margin between the data,taking into account the correct classification of the training set.

The effectiveness of SVM algorithm is because it combines two relevant ideas.The first is the change of landmark and input variables to another feature space.This double change simplifies the construction of nonlinear classifiers by using only the hyperplanes in the feature space.

The second consists in constructing separating hyperplanes in the feature space with the widest geometric margin possible [Vapnik (1998)].On the other hand,the SVM approach is based on a statistical foundation,a theory that easily justifies its statements.

The choice of the kernel functionkis very important;it must respect certain conditions and correspond to a scalar product in a high dimensional space.The conditions thatKmust satisfy to be a kernel function are as follows:It must be symmetric and positivesemi definite.

The simplest kernel function is the linear kernel:

Thus,in this case the linear classifier is used without changing the space.The kernel approach generalizes the linear approach.The linear kernel is sometimes used to evaluate the difficulty of a problem.

The kernels commonly used with SVM are expressed as follows:

Polynomial

Gaussian (RBF)

Laplacian

Sigmoid

Multi-class extensions

SVM is binary in their origin.However,real-world problems are in most cases multiclass.Therefore,multiclass SVM reduce the problem to a composition of several two-class hyperplanes to draw the decision boundaries between the different classes.

The principle is to decompose the examples into several subsets;each of them represents a binary classification problem.A separating hyperplane is determined for each problem by the binary SVM classifier.There are several decomposition methods in the literature,the most commonly used are:

2.1 One-against-all

This is the simplest and oldest method.According to Vapnik's formulation [Vapnik (1998)],it is a question of determining for each classka hyperplane Hk(wk,bk) separating it from all other classes.This classkis considered as the positive class (+1) and the other classes as the negative class (-1) so for a problem ofKclasses,K SVM binary is obtained.Fig.2 shows a case of separation of three classes.

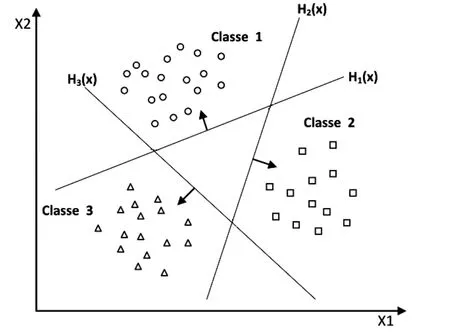
Figure 2:Approach One-against-all

2.2 One-against-one

This approach consists in using a classifier for each two classes.This method discriminates each class of every other class,thus K(K-1)/2 decision functions are learned.

For each pair of classes (k,s),this method defines a binary decision function.The assignment of a new example is done by voting list.An example is tested by calculating its decision function for each hyperplane.For each test,there is a vote for the class to which the example belongs (winning class).

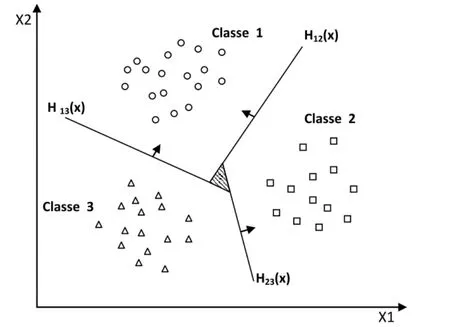
Figure 3:Approach One-against-one

3 Particle swarm optimization (PSO)

PSO is a stochastic optimization method developed by Eberhart and Kennedy in 1995 [Kennedy and Eberhart (1995)].Originally inspired by the world of life,more specifically the social behavior of swarming animals,such as schools of fish and flocks of birds [Li and Li (2014)].This method is based on a set of individuals called particles,originally arranged randomly,which can move in the search space.Each particle represents a solution to the problem and has a position Xiand velocity Vi.In addition,each particle has a memory that contains its best position visitedand the best G position among the positions of all particles.The evolution of the algorithm equations is given as follows:

where,ω represents the coefficient of inertia,the coefficients C1 and C2 are constants defined empirically according to the relation ship C1+C2≤ 4 and finally,R1 and R2 are random positive numbers that follow a uniform distribution over [0,1] [Kennedy and Eberhart (1995)].

The strategy of moving a particle is influenced by the following three components:

1.Inertia (ω Vi(t)):the particle tends to follow its current direction;

2.Cognitive component (C1R1(Pi-Xi)):The particle tends to move towards the best position already visited;

3.Social component (C2R2(G-Xi)):The particle tends to move towards the best position already reached by all the particles of swarm.

PSO for SVM model selection

The number of SVM model parameters depends on the type of kernel and their parameters.For example,the polynomial kernel has three parameters (γ,coef and d),therefore,the SVM model has four parameters if the regulation parameter C is added.In this case the search space is of dimension D=4.

The PSO algorithm maintains a set of particles.Each particle represents a candidate solution to the studied problem and considered as an object that has the following characteristics.

·The current position is a vector X =(x1,..,xD) where,x1,..,xDrepresents the values of SVM model parameters and D the dimension of the search space.

·The current velocity of the particle V=(v1,..,vD) is used to gradually modify the values of SVM model parameters according to Eqs.(7) and (8).

·The best position visited of the particle P =(p1,..,pD) is used to store the best parameter values found by the particle (a previous value of X).

·The best position among all particle positions G =(g1,..,gD)represents the best values of SVM parameters found so far.

The algorithm is expressed as follows:

4 Recognition system of handwritten Arabic characters

In the context of this study,a character recognition system has been developed.This section provides a brief description of the database and the technique used to extract the features.

A consistent database was built in SIMPA laboratory with the contribution of several researchers and students,containing 4840 examples of handwritten Arabic characters,as shown in Fig.4.The letters are in different positions (isolated,beginning,middle and end),for isolated letters there are 100×28=2800 images and for others there are 30× 68=2040 images.The number of classes is 28+68=96.

Figure 4:Samples from our database

For feature extraction,the image size was normalized to 70×70 and then the zoning technique [Anitha Mary and Dhanya (2015);Dinesh and Sabenian (2017)] was implemented.The principle is to divide the image into 49 zones or 10×10 pixel size blocks,and then count the number of black pixels in each zone.Fig.5 shows,for example,the letter ‘jim',which is written in Arabic ‘' in its isolated form.

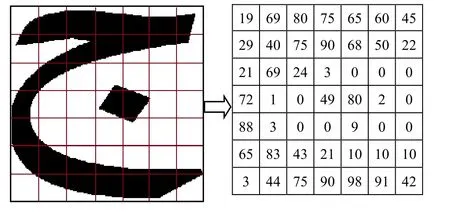
Figure 5:Feature extraction of letter “jim”

5 Implementation and results

In the framework of this research,an open-source SVM engine developed by Thorsten Joachims in 2008 was used.It is available at Joachims [Joachims (2008)],with documentation,examples and bibliographic references.

The selection of parameters is typically performed by minimizing the generalization error,so we used cross-validation (k-fold),this method consists of dividing the learning set into k disjoint subsets of the same size,then learn about the k-1 subsets,and test on the kthpart this process is repeated k times,the cross validation accuracy is obtained by calculating the average of k previous accuracy.In these experiments we used k=5 (5-fold).

First,the Grid Search method for SVM model selection was used to compare the results obtained with the PSO method.Since the Grid search is only used for selection of models that use few parameters (≤ 2),it was implemented with RBF and Laplacian kernel.There are two parameters,C and γ;the range of C used is [100,101,…,104,1015] and the range of γ is [10-15,10-14,…,101,102],for 16x18=288 iterations.

The results obtained for one-against-one approach are illustrated as follows:

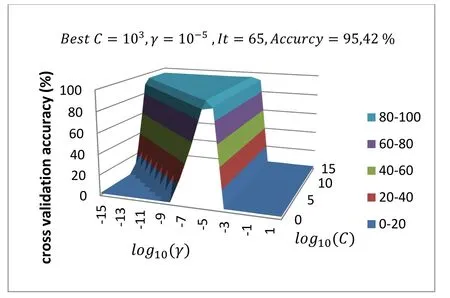
Figure 6:Grid search results for RBF kernel for one-against-one approach

Figure 7:Grid search results for Laplacian kernel for one-against-one approach For one-against-all approach,the results obtained are illustrated as follows:

Figure 8:Grid search results for RBF kernel for one-against-all approach

Figure 9:Grid search results for Laplacian kernel for one-against-all approach

According to these results,the surface area of the good results (Accuracy ＞90%) of Laplacian kernel is large compared to the RBF kernel,and the latter gave the best results.The same can be said about the two SVM approaches used,the surface of the good results of the one-against-all approach is large compared to the one-against-one,and the results of the latter are the best.

During these experiments,the CPU time (duration) was measured at each iteration,the results obtained are presented in Fig.10.The results show that the one-against-one approach (1×1) is faster than the other approach (1×N) and the Laplacian kernel is faster than the RBF.The one-against-all approach becomes very slow when theγparameter takes large values such as 1,10 and 100.This is evident in Fig.10 the iteration 18 and their multiples.

Figure 10:Time duration in seconds of each SVM model

Then,for the selection of SVM model parameters,the PSO method was used,in particular the gbest model [Frans (2006)].For these experiments,5 particles with coefficient values were used:ω=0.7298 and C1=C2=1.4962,to ensure convergence [Dang and Luong (2011)].

Each particle encodes the SVM model parameters;the number of these parameters is varied according to the type of kernel.The values considered are C ∈[100,1015],γ ∈[10-15,102],coef ∈[-10,102] and d ∈[1,10 ].If a particle exceeds the search space boundary,this particle will be repositioned at the boundary and its velocity is set to zero.The results obtained for one-against-one approach are expressed as follows:

Figure 11:Comparison results of different kernels for one-against-one approach

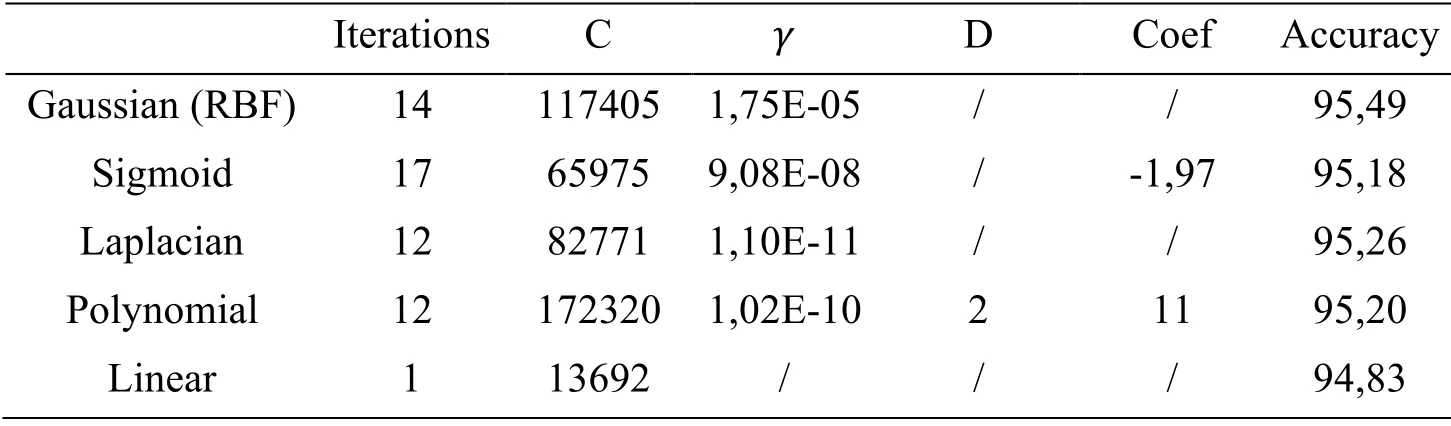
Table 1:Best results obtained for each kernel for one-against-one approach

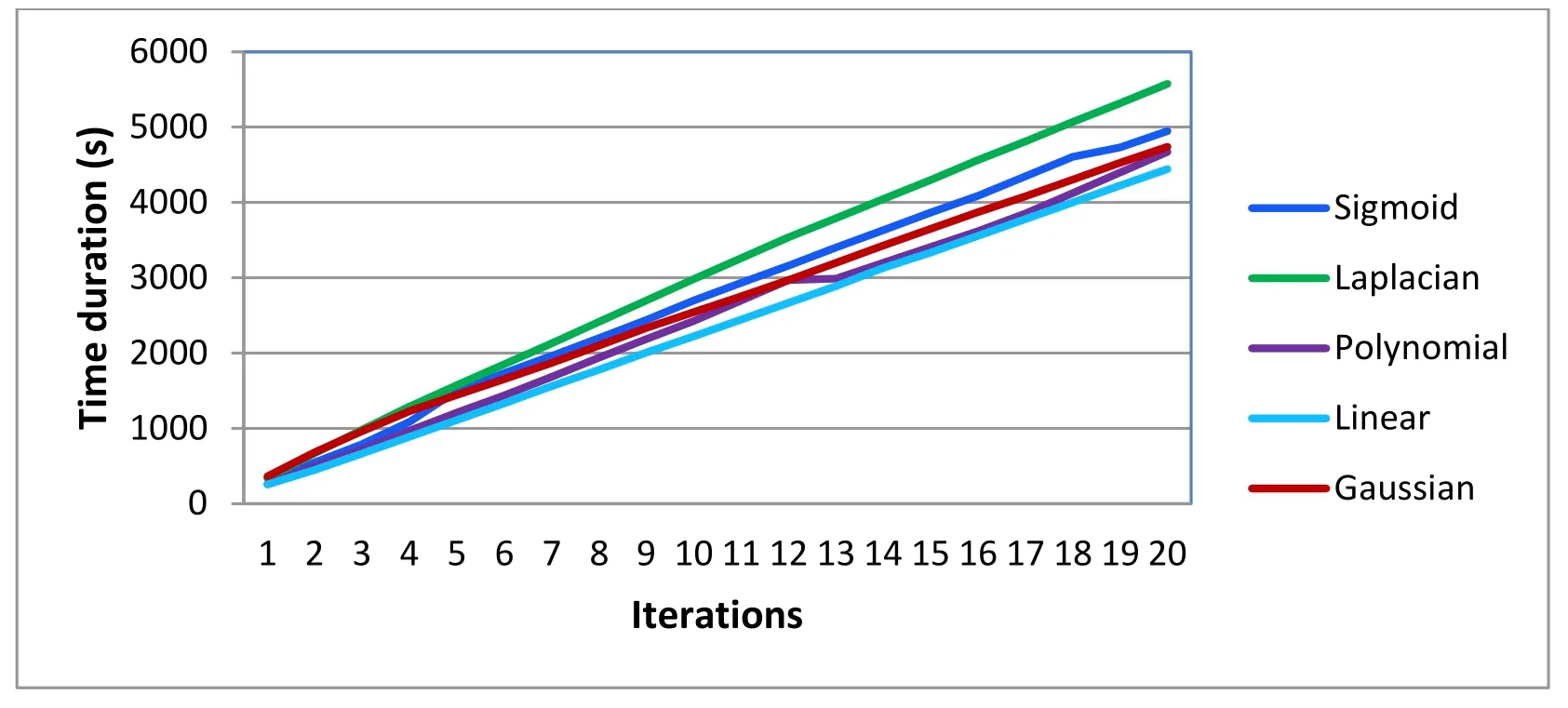
Figure 12:Time duration in seconds of each kernel for one-against-one approach

For one-against-all approach,the results obtained are expressed as follows:

Figure 13:Comparison results of different kernels for one-against-all approach

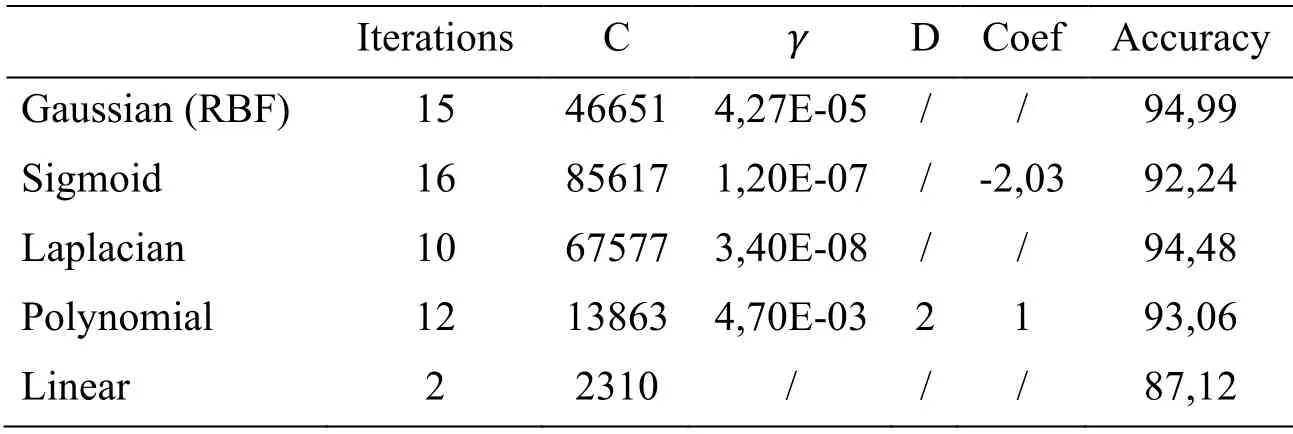
Table 2:The best results obtained for each kernel in one-against-all approach

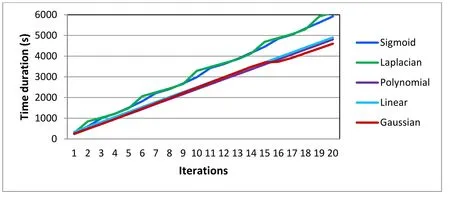
Figure 14:Time duration in seconds of each kernel for one-against-all approach

According to the results obtained,the linear kernel converges rapidly towards the optimum,because the SVM model has only one parameter (C),and the value of this parameter does not significantly affect the model's behavior.On the other hand,the sigmoid kernel is the slowest because in this case,there are three parameters and the model is very sensitive to the change of these parameters.The best result in terms of recognition rate is for the RBF kernel in one-against-one approach.

Finally,it can be noted that Grid Search is an effective technique to provide an overview of the search space (allows extracting promising regions),so to find good results it is necessary to use a local search or to launch the Grid Search a second time in the promising area.This method requires a lot of time to explore the search space.On the other hand,the PSO produces good results quickly.

6 Conclusions

Based on the experimental results obtained,the use of SVM approach for Arabic character recognition is strongly recommended due to its superior generalization ability to classify high-dimensional data,even when there is a large number of classes (in this case study:96 classes).

It is also important to note that the RBF kernel is the most suitable for the recognition of Arabic handwritten characters.Indeed this kernel has better results than the other kernels with a cross validation accuracy of 95,49% (SVM one-against-one,γ=1,75Ε-05).As a result,the PSO is more effective than Grid search in selecting SVM models.