Reduced Differential Transform Method for Solving Nonlinear Biomathematics Models

K.A.Gepreel,A.M.S.Mahdy,,M.S.MohamedandA.Al-Amiri

Abstract: In this paper,we study the approximate solutions for some of nonlinear Biomathematics models via the e-epidemic SI1I2R model characterizing the spread of viruses in a computer network and SIR childhood disease model.The reduced differential transforms method (RDTM) is one of the interesting methods for finding the approximate solutions for nonlinear problems.We apply the RDTM to discuss the analytic approximate solutions to the SI1I2R model for the spread of virus HCV-subtype and SIR childhood disease model.We discuss the numerical results at some special values of parameters in the approximate solutions.We use the computer software package such as Mathematical to find more iteration when calculating the approximate solutions.Graphical results and discussed quantitatively are presented to illustrate behavior of the obtained approximate solutions.

Keywords: Reduced differential transforms method,nonlinear biomathematics models,SI1I2R model,SIR model,analytic approximate solutions,qualitative analysis,stability and equilibrium.

1 Introduction

Many applications of science and engineering the nonlinear equations appear such as fluid dynamics,plasma physics,hydrodynamics,solid-state physics,optical fibers,acoustics and other disciplines [Adomian (1994)].The analyatic and approximate solutions many effective methods for obtaining to the NPDEs among of these methods are discussed in Ablowitz et al.[Ablowitz and Clarkson (1991);Singh,Dhar,Bhatti et al.(2016)].In the present article,we use the reduced differential transform method (RDTM) which discussed in Keskin et al.[Keskin and Oturanc (2010);Keskin (2010)];[Amer,Mahdy and Youssef (2018)],to construct an approximate numerical solution of some highly nonlinear differential equations in biomathematics.Reduced differential transform technique is iterative procedure a Taylor series solution of differential equations.This method reduces the size of work computational and easily applicable to many nonlinear physical problems.The results show that RDTM is a powerful mathematical tool for handling nonlinear ODEs.

The solution approach of RDTM is observed simpler than other approximate methods.Also,is highly accurate,rapidly converge and easily implementable mathematical tool for the multidimensional biomathematics models,physical problems emerging in various domains of engineering and applied sciences.Effectively,the analytic approximate solutions are discussed for two nonlinear systems of biomathematics models such as SI1I2R model for the spread of virus HCV-subtype4a and SIR childhood disease mode.These systems can be seen in El-Shahed et al.[El-Shahed,Ahmed and Abdelstar (2016);Haq,Shahzad,Muhammad et al.(2017)].In biomathematics models,they play a major role in various fields,such as Childhood diseases are the most serious infectious diseases.Measles,poliomyelitis,and rubella are famous among them.

1.1 SI1I2R model

Model SI1I2R for the spread of virus HCV-subtype4 can be written as follows [El-Shahed,Ahmed and Abdelstar (2016)]:

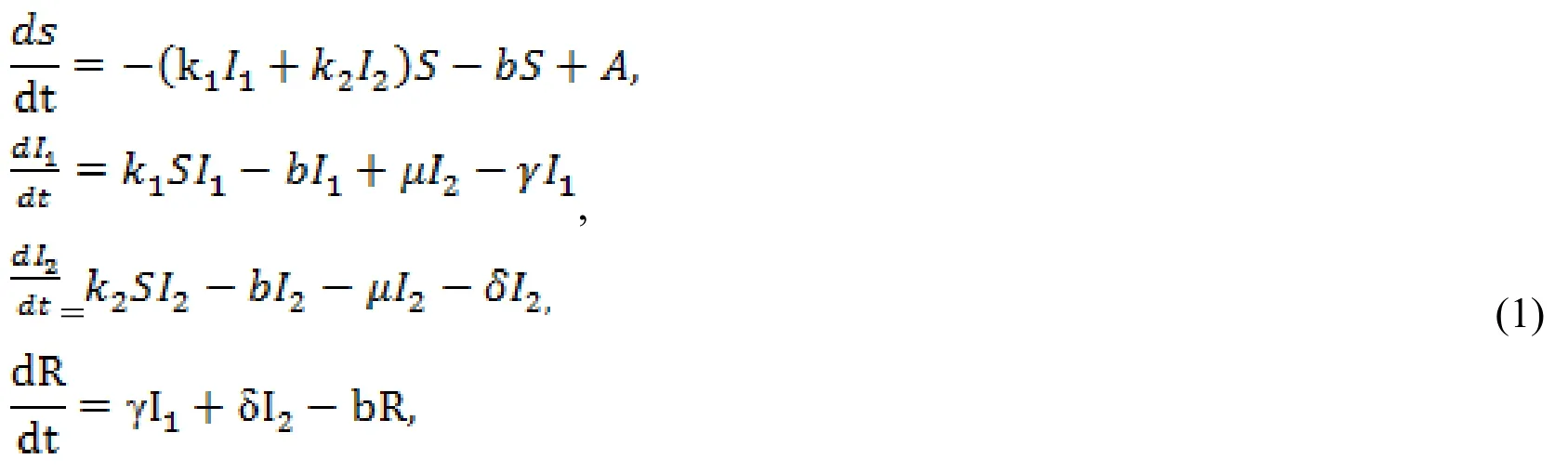
where R denotes densities of individuals recovered.Rate of birth is equal a rate positive constant (c),(b),δγ,rate the susceptible individuals a removed after taking the medicine from I1,I2,respectively.

1.2 SIR model

The mathematical model plays an important comprehend the process of transmission disease and provides different techniques to control propagation.Many mathematicians investigated childhood disease;for instance,Henderson et al.[Henderson (1984);Singh,Dhar,Bhatti et al.(2016)] studied the diseases vaccination of childhood.Makinde [Makinde (2007)] presented the Susceptible-Infected-Recovered.

This model shows vaccination is 100 percent efficient and rate the natural deathis unequal.So,size the total populationis not constant.Rate birth iswhile the rate of mortality of the childhood disease is very low.The parameter,is vaccinated population at birth,whererest of population is susceptible.The rate of susceptible individual suffers from through contact with infected individuals is.Rate the infected individuals recover is.More many applications of models fractional [El-Shahed,Ahmed and Abdelstar (2016);Haq,Shahzad,Muhammad et al.(2017)].Researchers and mathematicians used fractional models problems [El-Shahed,Ahmed and Abdelstar (2016);Henderson (1984)].

This paper are organized as follows.Preliminaries and notations of RDTM are given in Section 2.In Section 3,we apply the RDTM to solve two models of nonlinear biomathematics models (SI1I2R model for the spread of virus HCV-subtype4a and SIR childhood disease mode).In Section 4,we have shown the qualitative analysis for the model SIR.Conclusions are given in Section 5.

2 Preliminaries and notations

The basic idea,basic definitions and property properties of the RDTM are discussed in many new articles such as Mohamed et al.[Mohamed,Sayed and Al-Qarshi (2016);Keskin and Oturanc (2009);Keskin (2010)].We summarized the RDTM in the following Tab.1.

Table 1:The fundamental operations of RDTM

3 Numerical results

In this section,we used RDTM to construct analytic approximate solutions two systems of nonlinear biomathematics models (SI1I2R) model for the spread of virus HCVsubtype4a and SIR childhood disease mode.The results have been provided by software packages such as Mathematica 9.

3.1 Example 1

Let us consider SI1I2R model for the spread of virus HCV-subtype4a on homogenous networks is given by El-Shahed et al.[El-Shahed,Ahmed and Abdelstar (2016)]:

whereb=0.02,c=0.04,N=1000000,µ=0.02,γ=0.001,δ=0.001k1=0.42×10-6,k2=0.164×10-5.

Subject to the initial conditions:

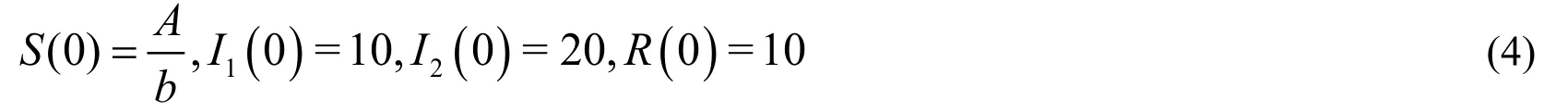
From RDTM,we have following itearation relations:

and so on.

By using the software Mathematica,we obtained the component ofS(t),I1(t),I2(t)andR(t) to the tenth iteration and we write two only for convenience.

Finally,the differential inverse transforms are given by:

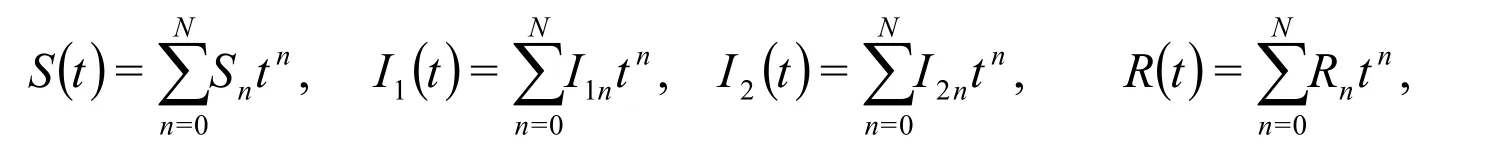
Consequently,the approximate series solutions take the form

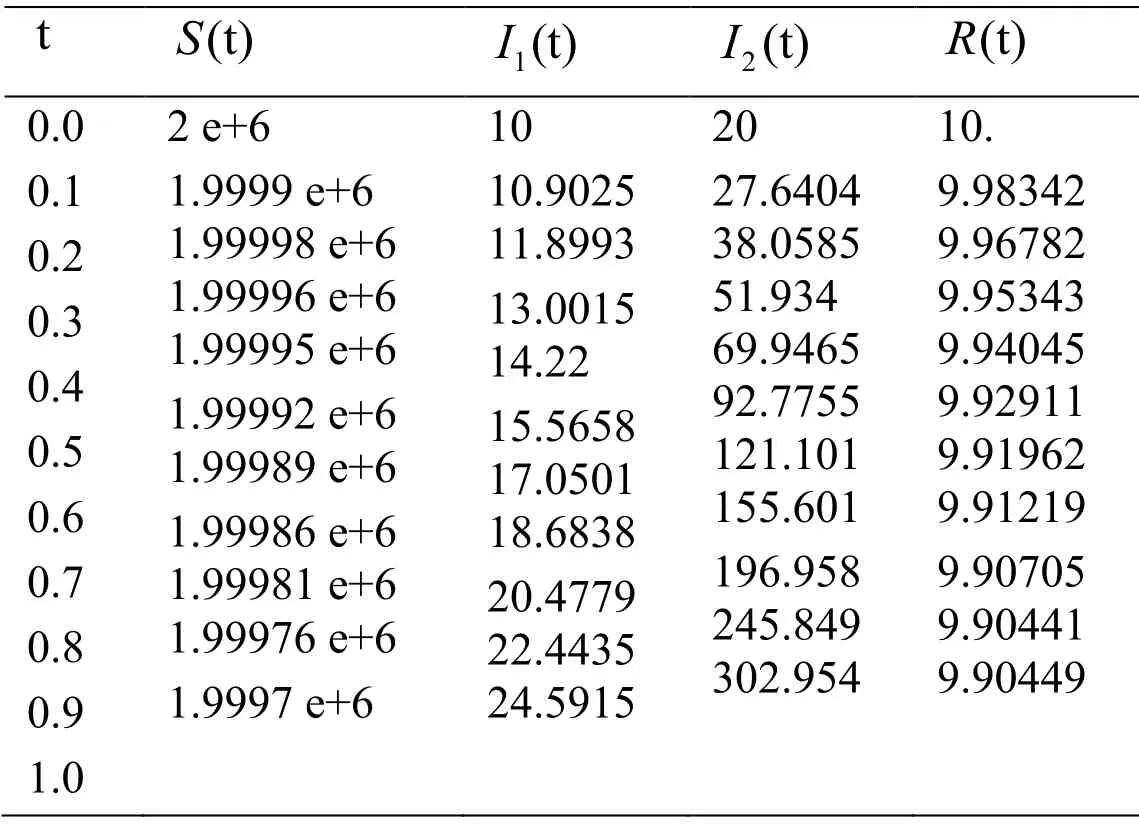
Table 2:Numerical solution of the proposed model using RDTM

Figure 1:Numerical simulations for the (S I1 I2 R) model at various for the social and infection

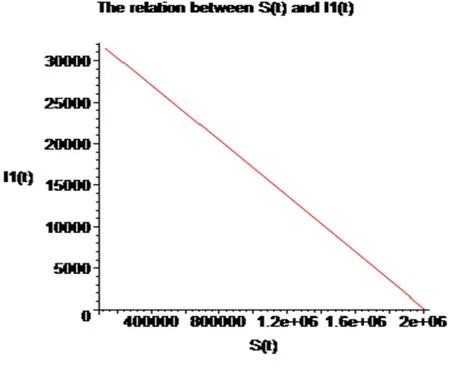
Figure 2:The relation between S(t) and I1(t)

Figure 3:The relation between S(t) and R(t)

Figure 4:The relation between I1 (t) and I2 (t)

Figure 5:The relation between I1 (t) and R(t)

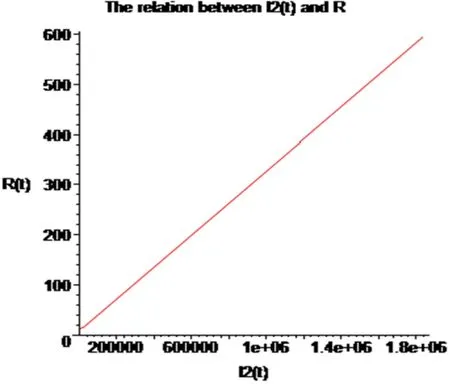
Figure 6:The relation between I2 (t) and R(t)

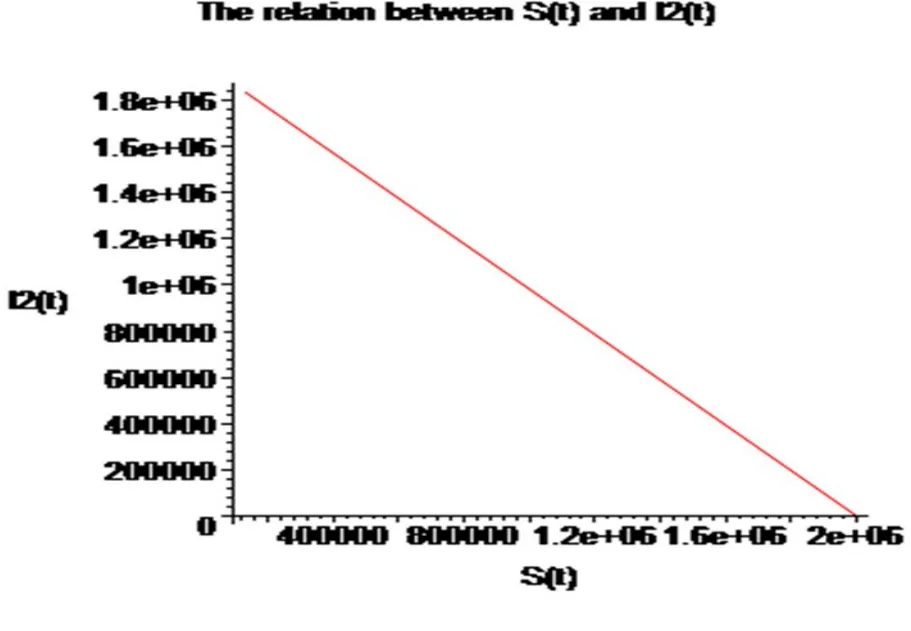
Figure 7:The relation between S(t) and I2 (t)

This approach of efficiency is greatly enhanced by calculation further terms ofS(t),I1(t),I2(t)andR(t) by using RDTM.Figs.(1)-(7) show the approximate solution of SI1I2R model.From Figs.2 to 7,showing the relation between S(t) andI1(t);I1(t) andI2(t);I1(t) and R(t);I2(t) and R(t);I2(t) and S(t).From the above Fig.2,we S(t) is decreasing with increasing theI1(t).Also,from Fig.3,we get S(t) is decreasing with increasing the R(t).From Fig.4,weI1(t) is increasing theI2(t).Fig.5,leads to getI1(t) is increasing the R(t).In Fig.6,I2(t) is increasing R(t).In Fig.7,S(t) is increasing theI2(t).

3.2 Example 2

Let us consider SIR model [Makinde (2007)]:

where 9,.0=p0.4,=µ0.03,=γ8.0=β,

with initial conditions:

First by applying RDTM on both sides of Eq.(8),thus we get :

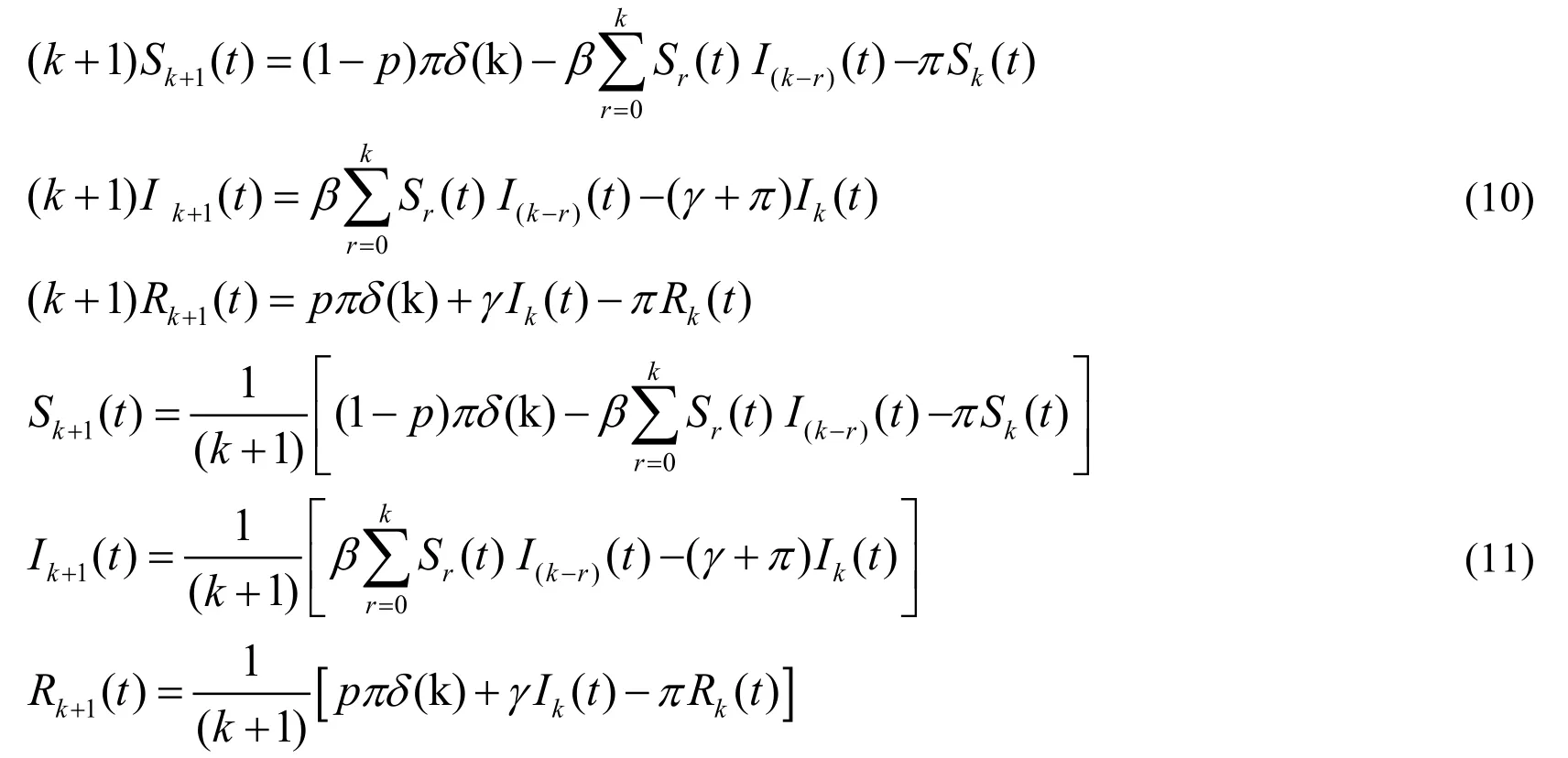
By substituting Eq.(9) in Eq.(11) we have :

and so on.

The components can obtain by Mathematica software.Taking transformation inverse to get following results.

Consequently,

Table 3:Coverage the various parameter values of effect of vaccination (pc=0.4625)

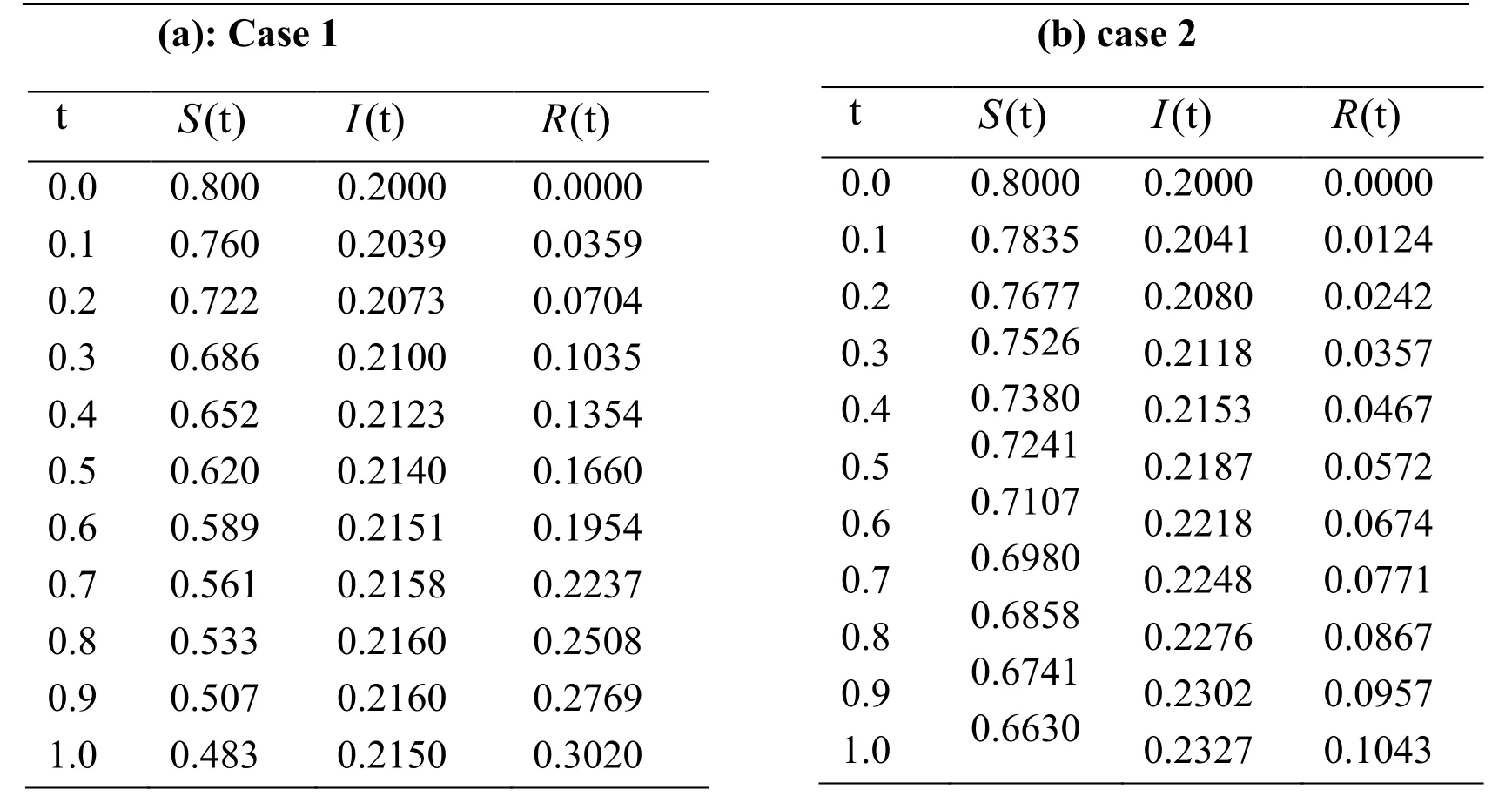
Table 4:Numerical solution of the proposed model using RDTM

4 Analysis qualitative of SIR

Observed,R is not appear in first and second Eq.(8),we analyze model qualitatively by studying subsystem in closed setThe subsystem described analysis qualitatively of the long-term behavior falls into two categories:die out or endemic.The solution asymptotically approaches a disease free equilibrium (DFE) at the disease dies out naturallyE0of the formE0=(1 -p,0).The stability of this equilibrium is reproduction number

The DF is locally stable ifRv＜ 1.Global asymptotic stability for DFE is also achieved using a Bendixson-Dulac argument forRv＜ 1 i.e.,there are no periodic solutions [Brauer and Castillo-Chavez (2001);Makinde (2007)].For many details of eigenvalues in Makinde [Makinde (2007)].

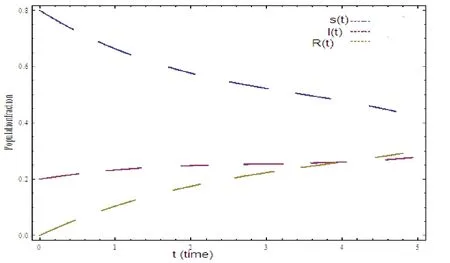
Figure 8:Population fraction versus time for Case1 at 0.9p=

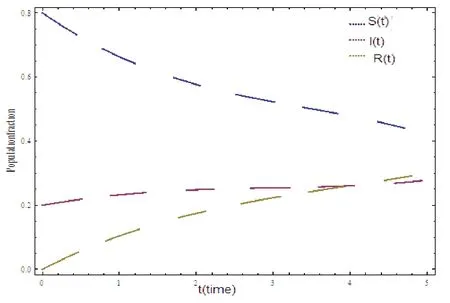
Figure 9:Population fraction versus time for Case2 at 0.3p=

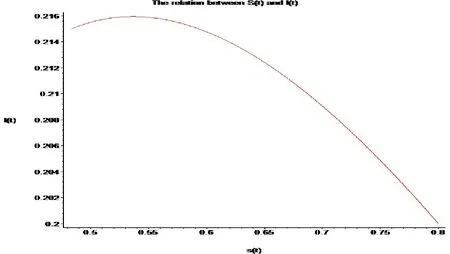
Figure 10:The relation between S(t) and I(t)

Figure 11:The relation between S(t) and R(t)

Figure 12:The relation between I(t) and R(t)

This approach of efficiency is greatly enhanced by calculation further terms ofS(t),I(t)andR(t) atp= 0.3 by using RDTM.From Figs.(9)-(12) show the approximate solution of SIR model.From Fig.10,the approximate solution S(t) is decreasing with increasing I(t).In Fig.11,the approximate solution S(t) is decreasing with increasing R(t).In Fig.12,the approximate solution I(t) is increasing with increasing R(t).

5 Discussion

In this work,we present new applications of the reduced differential transform method (RDTM) by handling two nonlinear biomathematics models (SI1I2R model for the spread of virus HCV-subtype4a and SIR childhood disease mode).RDTM,which does not require linearization,perturbation or discretization,form the solution of this method is convergent power series with elegantly computed components.So,the solution procedure is simpler than other traditional methods.

Acknowledgement:The authors are very grateful to referee for his valuable remarks and comments.

References

Abdou,M.A.(2007):The extended tanh-method and its applications for solving nonlinear physicalmodels.Applied Mathematics Computation,vol.190,pp.988-996.

Abdusalam,H.A.(2005):On an improved complex tanh-function method.International Journal Nonlinear Science Numerical Simulation,vol.6,no.2,pp.99-106.

Ablowitz,M.J.;Clarkson,P.A.(1991):Solitons Nonlinear Evolution Equations and Inverse Scattering Transform.Cambridge University Press,Cambridge.

Adomian,G.(1994):Solving Frontier Problems of Physics the Decomposition Method.Kluwer Acad.Publ.

Amer,Y.A.;Mahdy,A.M.S.;Namoos,H.A.R.(2018):Reduced differential transform method for solving fractional-order biological systems.Journal of Engineering and Applied Sciences,vol.13,no.20,pp.8489-8493.

Amer,Y.A.;Mahdy,A.M.S.;Youssef,E.S.M.(2018):Solving fractional integrodifferential equations by using sumudu transform method and Hermite spectral collocation method.Computers,Materials ＆ Continua,vol.54,no.2,pp.161-180.

Arrowsmith,D.K.;Place,C.M.(1982):Ordinary Differential Equations.Chapman and Hall.

Babolian,E.;Biazar,J.;Vahidi,A.R.(2004):The decomposition method applied to systems of Fredholm integral equationsof the second kind,Applied Mathematics Computation,vol.148,pp.443-452.

Brauer,F.;Castillo,C.C.(2001):Mathematical Models in Population Biology and Epidemiology.Springer-Verlag.

Chen,Y.;Wang,Q.(2005):Extended Jacobi elliptic function rational expansion method and abundant families of Jacobi elliptic functions solutions to (1+1) dimensional dispersivelong wave equation.Chaos,Solitons ＆ Fractals,vol.24,pp.745-757.

Elmaboud,Y.A.;Mekheimer,K.S.;Mohamed,M.S.(2015):Series solution of a natural convection flow for a Carreau fluid in a vertical channel with peristalsis using homotopy analysis method.Journal of Hydrodynamics,vol.27,no.6,pp.969-979.

El-Shahed,M.;Ahmed,A.M.;Abdelstar,I.M.E.(2016):Fractional calculus model for the hepatitis C with different types of virus genome.International Journal of Systems Science and Applied Mathematics,vol.1,no.3,pp.23-29.

Gepreel,K.A.;Abo-Dahab,S.M.;Mohamed,M.S.(2015):Analytical approximate solutions for the nonlinear differential-difference equations arising in nanotechnology.Journal of Computational and Theoretical Nanoscience,vol.12,no.6,pp.1040-1044.

Haq,F.;Shahzad,M.;Muhammad,S.;Wahab,H.A.;Rahman,G.(2017):Numerical analysis of fractional order epidemic model of childhood diseases.Discrete Dynamics in Nature and Society,vol.2017,pp.1-7.

Hassan,A.A.M.;Ibrahim,H.S.H.;Mahdy,A.M.S.;Ibrahim,M.G.M.(2014):A new solution of SIR model by using the differential fractional transformation method.International Journal of Engineering and Applied Sciences,vol.4,no.11,pp.12-21.

He,J.H.(2004):The homotopy perturbation method for nonlinear oscillators with discontinuities.Applied Mathematics Computational,vol.151,pp.287-292.

He,J.H.(2004):Variational principle for some nonlinear partial differential equations with variable coefficients.Chaos,Solitons and Fractals,vol.19,pp.847-851.

He,J.H.;Wu,X.H.(2006):Exp-function method for nonlinear wave equations.Chaos,Solitons and Fractals,vol.30,pp.700-708.

Henderson,R.H.(1984):The expanded programmer on immunization of the world health organization.Reviews of Infectious Diseases,vol.6,no.2,pp.475-479.

Hirota,R.(1971):Exact solution of the KdV equation for multiple collisions of solutions.Physical Review Letters,vol.27,pp.1192-1194.

Keskin,Y.(2005):Solving Differential Equations by the Differential Transformation Method(Ph.D.Thesis),Selcuk University,Turkish.

Keskin,Y.;Oturanc,G.(2009):Reduced differential transform methodfor partial differential equations.Intational Journal Nonlinear Science Numerical Simulation,vol.10,no.6,pp.741-749.

Keskin,Y.;Oturanc,G.(2010):Reduced differential transform method for generalized KdV equations.Mathematical and Computational Applications,vol.15,no.3,pp.382-393.Keskin,Y.;Oturanc,G.(2010):The reduced differential transformmethod:a new approach to fractional partial differentialequations.Nonlinear Science Letter A,vol.1,no.2,pp.207-217.

Liu,H.M.(2004):Variational approach to nonlinear electrochemical system.International Journal Nonlinear Science,vol.5,no.1,pp.95-96.

Liu,H.M.(2005):Generalized variational principles for ion acoustic plasma waves by He's semi-inverse method.Chaos Solitons Fractals,vol.23,no.2,pp.573-576.

Lu,D.(2005):Jacobi elliptic function solutions for two variant Boussinesq equations.Chaos,Solitons and Fractals,vol.24,pp.1373-1385.

Mabood,F.;Khan,W.A.(2014):Combined analytical-numerical solution for MHD viscous flow over a stretching sheet.Journal of Computational Engineering,pp.1-7.

Mabood,F.;Khan,W.A.;Ismail,A.I.(2014):Optimal homotopy asymptotic method for heat transfer in hollow sphere with Robin boundary conditions.Heat Transfer-Asian Research,vol.43,no.2,pp.124-133.

Makinde,O.D.(2007):Adomian decomposition approach to a SIR epidemic model with constant vaccination strategy.Applied Mathematics and Computation,vol.184,no.2,pp.842-848.

Miura,M.R.(1978):Backlund Transformation.Springer-Verlag,Berlin.

Mohamed,M.S.;Elagan,S.K.;Gepreel,K.A.;Elosimy,A.(2014):Optimal q- homotopy anaylsis method for nonlinear partial fractional gas dynamics equation.Jokull Journal,vol.64,no.9,pp.317-326.

Mohamed,M.S.;Sayed,M.;Al-Qarshi,T.T.(2016):Approximate solution to system of nonlinear partial differential equations using reduced differential transform method.Journal of Information and Computing Science,vol.11,no.4,pp.251-261.

Rogers,C.;Shadwick,W.F.(1982):Backlund Transformations.Academic Press,New York.

Singh,H.;Dhar,J.;Bhatti,H.S.;Chandok,S.(2016):An epidemic model of childhood disease dynamics with maturation delay and latent period of infection.Modeling Earth Systems and Environment,vol.2,no.79,pp.1-8.

Wang,M.L.;Zhou,Y.B.;Li,Z.B.(1996):Application of a homogeneous balance method to exact solutions of nonlinear equations in mathematical physics.Physical LettersA,vol.216,pp.67-75.

Wang,M.;Li,X.(2005):Extended F-expansion and periodic wave solutions for the generalized Zakharov equations.Physical LettersA,vol.343,pp.48-54.

Wang.D.S.;Ren,Y.J.;Zhang,H.Q.(2005):Further extended sinh-cosh and sin-cos methods and new non traveling wave solutions of the (2+1)-dimensional dispersive long wave equations.Applied Mathematical E-Notes,vol.5,pp.157-163.

Weiss,J.;Tabor,M.;Garnevalle,G.(1983):The Painleve property for partial differential equations.Journal Mathematical Physics,vol.24,pp.522-526.

Zayed,E.M.E.;Gepreel,K.A.(2009):The (G’/G)-expansion method for fnding traveling wavesolutions of nonlinear PDEs in mathematical physics.Journal Mathematical Physics,vol.50,pp.013502-013513.

Zayed,E.M.E.;Zedan,H.A.;Gepreel,K.A.(2004):Group analysis and modified tanh-functionto find the invariant solutions and soliton solution for nonlinear Euler equations.Intational Journal Nonlinear Science Numerical Simulation,vol.5,pp.221-234.

Zayed,E.M.E;Nofal,T.A.;Gepreel,K.A.(2009):The travelling wave solutions for non-linear initialvalue problems using the homotopy perturbation method.Applicable Analysis,vol.88,no.4,pp.617-634.

Zhang,S.(2008):Application of Exp-function method to higher dimensional nonlinear evolutionequation.Chaos,Solitons and Fractals,vol.38,pp.270-276.

Zhang,S.(2008):Application of Exp-function method to Riccati equation and new exact solutionswith three arbitrary functions of Broer-Kaup-Kupershmidt equations.Physical Letters A,vol.372,pp.1873-1880.

Zhang,S.L.;Wu,B.;Lou,S.Y.(2002):Painleve analysis and special solutions of generalized Broer-Kaup equations.Physical Letters A,vol.300,pp.40-48.

Zhang,S.;Xia,T.C.(2006):Symbolic computation and new families of exact nontraveling wavesolutions to (3+1)-dimensional Kadomtsev-Petviashvili equation.Applied Mathematics Computation,vol.181,pp.319-331.