Quantum Communication Networks and Trust Management:A Survey

Shibin ZhangYan ChangLili YanZhiwei ShengFan YangGuihua HanYuanyuan Huang and Jinyue Xia

Abstract: This paper summarizes the state of art in quantum communication networks and trust management in recent years.As in the classical networks,trust management is the premise and foundation of quantum secure communication and cannot simply be attributed to security issues,therefore the basic and importance of trust management in quantum communication networks should be taken more seriously.Compared with other theories and techniques in quantum communication,the trust of quantum communication and trust management model in quantum communication network environment is still in its initial stage.In this paper,the core technologies of establishing secure and reliable quantum communication networks are categorized and summarized,and the trends of each direction in trust management of quantum communication network are discussed in depth.

Keywords: Quantum communication,quantum communication network,trust,trust management,trust management model.

1 Introduction

Quantum communication is a new cross discipline combining classical information theory and quantum mechanics,which uses quantum state to carry information.Quantum communication is expected to break through the limit of classical communication technology in the aspects of communication security,computing power,information transmission,channel capacity and measurement accuracy,which has become a new direction and will be the mainstream in the field of communication and information in twenty-first century.Quantum communication is a strategic area which is related to national information security and national security,and it is possible to change the future development of the information industry.As a result,the major developed countries in the world take it as a priority in the development of information technology and industry heights.The government and the relevant departments of our country have attached great importance to the research of quantum communication and network.A number of achievements with international advanced level have been achieved.

Compared to the classical communication (the security of classical secure communication has not been proved),a significant advantage of quantum communication is that it can achieve the security of strict mathematical proof (absolute security) [Wu,Wang and Pan (2014)].Quantum communication is to break the shackles of traditional secure communication technology based on the unique characteristics of quantum states,which using quantum information carried by microscopic particles to realize secure communication.The uncertainty principle and non-cloning principle provide the theoretical basis for quantum secure communication,which will show a great application prospect in the field of information security.

The application of quantum communication theory and technology cannot be separated from the quantum communication network.Its ultimate goal is to build an absolutely secure wide area network and even a global quantum communication network.However,due to the fact that the non-ideal physical device used in the quantum communication cannot fully meet the mathematical physical model,there are some uncertainty and practical security problems in the future quantum communication network [Xu,Liu,Mao et al.(2014)] (For example,the problem of trust in quantum communication networks,etc).With the development of the practical application of quantum communication technology,quantum communication is moving towards high speed,long distance and network development from traditional simple point-to-point communication.In the near future,quantum secure communication will serve as the key technology to ensure the security of future information society.Quantum communication is likely to enter thousands of households and becomes a driver of comprehensive e-government,ecommerce,e-medicine,bio-feature transmission and intelligent transmission system,and other electronic services.Quantum communication will provide basic security services and the most reliable security for today's highly information-based society.

To promote the practical application of quantum communication and network,security is an urgent problem to be solved.How to ensure the reliability of each node (user) in the quantum communication network and prevent counterfeiting,tampering,hacking,denial and deception,are the key to ensure the practical and network of quantum communication.As a matter of fact,similar with the classical network,trust is the premise and foundation of quantum secure communication.The existing quantum secure communication protocols and technologies are implicitly related to trust,assuming some kind of trust,or with the purpose of creating or gaining some kind of trust relationship.But trust cannot simply be attributed to security issues,we should see the fundamental role and importance of trust management model in the quantum communication network.Up to now,many researches have been made on the theory and technology of quantum communication and quantum communication networks.But the research on trust and trust management model for quantum communication is not much.Therefore,the research of quantum trust management model in the quantum communication network has both theoretical and practical significance,which will become a hotspot.

2 The status of research on quantum communication

The research of quantum communication started since 1980s [Wu,Wang and Pan (2014)],mainly including:QKD (quantum key distribution),QT (quantum teleportation),QSS (Quantum secret sharing),QSDC (Quantum secure direct communication),QIA (Quantum identity authentication),QS (Quantum signature),QBC (Quantum bit commitment),QCT (Quantum coin toss),QOT (Quantum oblivious transfer),SMQC (Secure multiparty quantum computation) and so on,one of the most studied is QKD.

2.1 Quantum key distribution (QKD)

The research on quantum cryptography can be traced back to 1969.Wiesner in Columbia University first thought of using the theory of quantum mechanics to protect information security and made use of the single quantum state to make the unforgeable electronic money.However,this idea was not achieved because of the short life of single quantum state.Inspired by this idea,Bennett in IBM and Brassard in the University of Montreal in Canada proposed the concept of QKD and the first QKD protocol (BB84 protocol) [Bennett and Brassard (1984)] in 1984,which marked the beginning of the study of quantum cryptography.After that,Ekert proposed E91 protocol [Ekert (1991)] in 1991,and Bennett proposed B92 protocol [Bennett (1992)] in 1992.At present,quantum communication has been gradually moving towards practical application from the pure theory research.In 2000,the Canadian Jennewein Thomas research group completed the long distance QKD experiment using entangled photons [Jennewein,Simon,Weihs et al.(2000)].In the same year,the transmission distance of QKD in free space reached 1.6 km in the Alamos Los Laboratory of the United States [Buttler,Hughes,Lamoreaux et al.(2000)].In 2002,the “plug and play” scheme was used and the quantum key transmission of 67 km was successfully carried out in the optical fiber [Stucki,Gisin,Guinnard et al.(2002)].In the same year,German and Britain scientists realized QKD with 23.4 km between Zugspitze peak and Calvin Del by using the laser photon [Kurtsiefer,Zarda,Halder et al.(2002)].In 2003,Zeng's group completed the 50 Km quantum secret system experiments with optical fiber and the development of the prototype [Zhou,Wu,Chen et al.(2003)].In 2004,Guo's group completed fiber quantum key transmission more than 125 Km between Beijing and Tianjin [Guo (2008)].In 2006,Pan's team,the Los Alamos laboratory,University of Munich in Europe-Vienna University joint research team realized the experiment of decoy state quantum key distribution with more than 100 kilometers,which opened the door to the application of quantum secure communication [Wang (2007)].In 2010,the Tokyo QKD developed by 9 institutions including Japan and Europe put into operation [Sasaki,Fujiwara,Ishizuka et al.(2011)].In 2012,Pan's team achieved quantum teleportation and entanglement distribution in free space with one hundred kilometers for the first time in the world [Yin,Ren,Lu et al.(2012)].In 2013,Cambridge Research Laboratory of Toshiba Company claimed that the study of QKD technology was more practical,which was closer to being widely used by commercial,banking,and government agencies [Fröhlich,Dynes,Lucamarini et al.(2013)].In 2014,Pan's team implemented a remote quantum key distribution system withstanding hacker attacks,which extended transmission distance to 200 km (a new world record) [Tang,Yin,Chen et al.(2014)].In recent years,some new theories and techniques of QKD protocol have been put forward.In 2007,Boyer et al.put forward semi-QKD protocol [Boyer,Kenigsberg and Mor (2007)].In 2009,Noh presented the first anti-fact quantum cryptography scheme [Noh (2009)],which realized key distribution by using quantum counter intuitive effect of quantum interference.Device independent QKD protocols were also proposed [Hardy and Kent (2005);Acín,Gisin and Masanes (2006);Hänggi,Renner and Wolf (2010);Sun,Peng,Shen et al.(2012);Ferreira da Silva,Vitoreti,Xavier et al.(2013);Masanes,Renner,Christandl et al.(2014);Bacco,Christensen,Castaneda et al.(2016);Roberts,Lucamarini,Dynes et al.(2017);Pereira and Pirandola (2018)],in which the safety is independent with equipment parameters,security is not guaranteed by the fundamental principles of quantum mechanics,but rather than the nonsignal theorem based on the theory of relativity.The biggest advantage of device independent QKD is that even if the quantum mechanics is not established,it can still provide unconditional secure key distribution.

2.2 Quantum teleportation (QT)

Quantum teleportation,as one of the important fields in research of quantum communication,plays an important role in the field of quantum computation and quantum communication.In 1993,six scientists from Bennett and other 4 countries put forward the first quantum teleportation scheme [Bennett,Brassard and Crépeau (1993)],which ushered a new era of quantum teleportation.In 1994,Davidovich et al.proposed a quantum state transfer scheme based on Bell basis measurement [Davidovich,Zagury,Brune et al.(1994)].In 1997,Guo's team proposed quantum teleportation scheme based on quantum cavity electrodynamics [Zheng and Guo (1997)].For the first time,a research group in Austria successfully demonstrated the quantum teleportation experimentally (The results have made a stir in the international academic circles) [Nielsen,Knill and Laflamme (1998)].In 2000,the Photoelectric Institute of Shanxi University proposed a quantum teleportation scheme by using bright squeezed light.Li et al.presented a probabilistic teleportation scheme for single particle quantum states theoretically [Li,Li and Guo (2000)].In 2001,Shih's team in University of Maryland successfully achieved quantum teleportation experiments using nonlinear methods [Kim,Kulik and Shih (2001)].In 2002,Guo's team realized the teleportation of three particle entangled W states by using non-maximally entangled state as quantum channel [Zheng,Gu and Guo (2002)].In 2003,Roa et al.proposed a teleportation scheme for d dimensional quantum system [Roa and Dolgado (2003)].In 2005,Pan's team created a world record of two-way quantum entanglement distribution with 13 km in Hefei [Peng,Yang,Bao et al.(2005)].In 2012,Pan's team achieved the hundred kilometers quantum teleportation and entanglement distribution in free space for the first time in the world,which laid technical foundation for launching the first quantum communication satellite [Yin,Ren,Lu et al.(2012)].In the same year,the scientists at University of Vienna and Austria Academy of sciences realized the most distant teleportation of a quantum state (143 Km) [Ma,Herbst,Scheidl et al.(2012)].In recent years,quantum teleportation has attracted a large number of scholars,and some effective quantum teleportation schemes have been proposed [Ye and Lin (2013);Knoll,Schmiegelow and Larotonda (2013);Pfaff,Hensen,Bernien et al.(2014);Pirandola,Eisert,Weedbrook et al.(2015);Yang,Ma,Zheng et al.(2017);Huo,Qin,Cheng et al.(2018)],which have promoted the development of quantum communication.

2.3 Quantum secret sharing (QSS)

Secret sharing is an important branch of cryptography.Quantum secret sharing (QSS) is the quantum generalization of classical secret sharing.QSS is realized based on quantum mechanics rather than mathematical problems or computational complexity,so it is more secure.Since 1999,Hillery et al.first proposed a QSS protocol based on multi-particle entangled state [Hillery,Buzek and Berthiaume (1999)],many scholars have carried out a lot of researches in theory and experiment,QSS protocol for sharing arbitrary single quantum bits [Tittel,Zbinden and Gisin (2001);Xiao,Long,Deng et al.(2004);Zhang,Li and Man (2005);Zhang,Liu and Li (2011)],QSS for sharing two quantum bits [Karlsson,Koashi and Imoto (1999);Guo and Guo (2003);Dong,Xiu and Gao (2007)],QSS for sharing multi quantum bits [Hillery,Buzek and Berthiaume (1999);Xiao,Long,Deng et al.(2004);Deng,Yan,Li et al.(2005);Yang and Wen (2008);Gao,Yan and Li (2009)] are proposed.In 1999,Karlsson et al.presented a QSS protocol by using Bell state [Karlsson,Koashi and Imoto (1999)].Cleve et al.first proposed a QSS protocol with (m,n) threshold by using the properties of quantum error correcting codes [Cleve,Gottesman and Lo (1999)].In 2001,Tittel et al.realized QSS in experiment [Tittel,Zbinden and Gisin (2001)].In 2003,Guo et al.proposed QSS protocol by using product states [Guo and Guo (2003)].In 2004,Li et al.proposed an efficient multi-party QSS [Xiao,Long,Deng et al.(2004)].In 2005,Deng et al.proposed a QSS scheme based on arbitrary two particle state [Dong,Xiu and Gao (2007)].Zhang et al.proposed multiparty QSS protocol and threshold QSS protocol based on single photons [Zhang,Li and Man (2005)].Yan et al.proposed QSS scheme between multi-parties based on nonentangled states [Yan and Gao (2005)].In 2008,Yang et al.put forward QSS scheme between multi-parties based on threshold [Yang and Wen (2008)].In 2009,Gao et al.presented QSS scheme between multi-parties based on six particles quantum state [Gao,Yan and Li (2009)].In 2011,Zhang et al.proposed a QSS protocol based on quantum error correcting codes [Zhang,Liu and Li (2011)].In 2013,Sun et al.proposed an extension of quantum secret sharing network [Sun,Xu,Chen et al.(2013)].In 2014,Bell et al.studied and carried out the experimental demonstration of diagram state QSS [Bell,Markham,Wadsworth et al.(2014)].In 2015,Karimipour et al.presented realizing QSS by using single photons [Karimipour and Asoudeh (2015)].

From the analyses made above,we can find that a lot of new and efficient QSS protocols have been designed both in theory and experiment,which has promoted the development of quantum communication greatly.

2.4 Quantum secure direct communication (QSDC)

In recent years,as another branch of quantum cryptography,quantum secure direct communication (QSDC) has attracted much attention of scholars.QSDC is a new communication form different from QKD.The differences between QKD and QSDC are that QSDC transmits secret information in quantum channel directly.In 2000,Long et al.designed an efficient QKD scheme by using Bell states,which is essentially a two-step QSDC scheme [Long and Liu (2002)].Since 2001,Beige et al.put forward the concept of “deterministic secure communication” for the first time [Bege,Englert,Kurtsiefer et al.(2002);Bege,Englert,Kurtsiefer et al.(2002)],and QSDC began to attract people's attention.In 2002,Bostrom et al.proposed the famous “Ping-Pong” protocol based on entanglement [Bostrom and Felbinger (2002)].In 2003,Deng et al.proposed a two-step QSDC protocol based on EPR pairs [Deng,Long and Liu (2003)].In 2004,Deng et al.designed a QSDC protocol by using single photon sequence as quantum one-time pad [Deng and Long (2004)].In 2005,Lucamarini et al.proposed a QSDC protocol without entanglement [Lucamarini and Mancini (2005)].A high dimensional QSDC protocol based on dense coding was proposed by Wang et al.[Wang,Deng,Li et al.(2005)].In 2006,Lee et al.proposed a QSDC protocol with authentication function [Lee,Lim and Yang (2005)],which can prevent active attacks effectively.In 2008,Liu et al.proposed a more efficient QSDC protocol based on authentication [Liu,Chen,Li et al.(2008)].In 2010,Liu et al.also put forward a QSDC protocol based on authentication [Liu,Pei,Quan et al.(2010)].In 2011,Wu et al.put forward another QSDC scheme based on entangled states [Wu,Zhai,Cao et al.(2011)].In 2013,Chang et al.proposed a QSDC and authentication protocol using single photons [Chang,Xu,Zhang et al.(2013)].In 2014,Yuan et al.proposed a deterministic secure quantum communication (DSQC) scheme by using GHZ states [Yuan,Zhang,Hong et al.(2014)].In 2015,Li et al.proposed controlled quantum secure direct communication (CQSDC) protocol based on five atom cluster states using cavity quantum electrodynamics [Li,Li and Nie (2015)].In 2017,Bai et al.propsoed quantum secret sharing by using orthogonal multiqubit entangled states [Bai,Li,Liu et al.(2017)].In 2018,Qin et al.propsoed multiparty to multiparty quantum secret sharing [Qin,Tang and Tso (2018)].

In fact,QSDC is one of the main research branches of quantum communication system.It has received extensive attention in recent years because it transmits secure information directly without generating quantum key first.However,the research of QSDC is mainly focused on the design of QSDC protocol,and most protocols designed are in ideal environment.Obviously,the research of QSDC has a certain distance from the practical.

2.5 Quantum identity authentication (QIA)

To realize secure quantum communication,identity authentication is also very important.Since the classical authentication method is not unconditional secure,it cannot effectively prevent the attacker to pretend to be a legitimate correspondent.If the attacker controls the quantum channel and classical channel,he can succeed in middle-man attack.Therefore,identity authentication between the two sides in one communication is imperative.In recent years,researchers have proposed a variety of quantum identity authentication (QIA) schemes.In 1999,Duek et al.put forward a secure QIA system,which combining the classic authentication process with the quantum key distribution [Dusek,Haderka,Hendrych et al.(1999)].In 2000,Ljunggren et al.achieved the purpose of certification by inserting the quantum sequence generated by shared information previously in particles of BB84 protocol [Ljunggren,Bourennane and Karlsson (2000)].In 2001,Gurty et al.proposed a QIA scheme,in which Bob verified the identity of Alice with the help of Trent by operating three particle entangled states [Gurty and Santors (2012)].In 2002,Mihara presented three QIA schemes based on entanglement and unitary operations [Mihara (2002)].In 2003,Zeng et al.proposed that the encoded measurement basis based on shared information previously can be used to verify the identities between two sides,and the entangled states can be used to ensure the security of information transmitted [Zeng and Zhang (2001);Zhou,Zeng,Zeng et al.(2005)].In 2006,Zhang et al.proposed a one-way QIA scheme based on ping-pong protocol and quantum controlled not gate [Zhang,Zeng,Zhou et al.(2006)].In 2008 and 2009,Yang et al.put forward two multi-party simultaneous QIA protocols based on single photons [Yang and Wen (2008)] and GHZ states [Yang and Wen (2009)] respectively.In 2011,Gao et al.proposed a QSDC and authentication scheme based on Bell state [Gao,Qin,Guo et al.(2011)].In 2013,Yang et al.proposed a QIA protocol with quantum (t,n) threshold based on GHZ states [Yang,Wang,Jia et al.(2013)].In 2014,Yuan et al.put forward a QIA scheme based on non-entanglement “Ping-Pong” technology [Yuan,Liu,Pan et al.(2014)].In 2015,Zhandry et al.proposed a secure authentication scheme based on encryption in the quantum random oracle model [Zhandry (2012)].In 2016,Ma et al.proposed continuous-variable quantum identity authentication based on quantum teleportation [Ma,Huang,Bao et al.(2016)].In 2019,Zawadzki proposed quantum identity authentication without entanglement [Zawadzki (2019)].

From the analyses made above,we know that quantum identity authentication plays an important role in quantum communication network.How to achieve efficient user identity authentication in large scale networks is a hot topic.At present,most quantum identity authentication is still a point to point authentication,which is low efficiency and lead to waste of classical and quantum resources.We are also pleased to see that some scholars also paid close attention to these problems and put forward multi-party quantum identity authentication protocols.

2.6 Quantum Signature (QS)

Most of the traditional digital signature algorithms are based on the assumption of not been proved computation complexity,for example,the difficulty of large integer factorization and discrete logarithm problem solving.However,the quantum algorithm can decompose large integer and solve discrete logarithm in polynomial time [Shor (1994)].As a result,most of the current digital signature schemes will fail if the quantum computer is successfully applied.Therefore,the design of quantum signature (QS) algorithm which can resist the attack of quantum computer is a hot topic.

In recent years,signature based on quantum mechanics has achieved a lot of results.In 2001,Zeng et al.proposed the first arbitration QS scheme based on symmetric cryptosystem [Zeng,Ma,Wang et al.(2011)].Gottesman et al.also proposed a real QS scheme based on quantum one-way function in the same year [Gottesman and Chuang (2001)].In 2002,Zeng et al.put forward an arbitration QS scheme with appendix by using the relevance between quantum one-time pad and GHZ state [Zeng and Keitel (2002)],and further improved the scheme in 2007 [Zeng (2008)].In 2004,Lee et al.proposed two arbitration QS scheme with message recovery [Lee,Hong,Hyunsang et al.(2004)].However,because entanglement is not used in this scheme,GHZ state can be replaced with the classical correlation state.In 2005,Lü et al.proposed an arbitration QS scheme based on quantum one-way function [Lü and Feng (2005)],which realized the signature of unknown quantum state.In 2006,Wang et al.proposed a new arbitration QS scheme with message recovery based on quantum one-time pad and quantum key distribution [Wang,Zhang and Tang (2006)],in which particles are measured with von Neumann method and entangled states are not needed.In 2007,Wang et al.put forward an arbitration QS protocol with appendix by using the hash function,which realizes the message signature of any bit [Wang,Zhang and Tang (2008)].In 2008,Yang et al.proposed a multi-proxy quantum group signature scheme with threshold shared verification [Yang (2008)].In 2010,Wen et al.presented a quantum group signature scheme based on quantum teleportation [Wen,Tian,Ji et al.(2010)].In 2011,Xu et al.proposed a quantum blind signature scheme for a distributed electronic voting system based on the properties of group signature and blind signature [Xu,Huang,Yang et al.(2011)].In 2012,Yin et al.put forward a blind signature scheme based on χ-type states [Yin,Ma,Liu et al.(2012)].In 2013,Wen et al.proposed an electronic payment scheme among banks based on quantum proxy blind signature [Wen,Chen and Fang (2013)].In 2014,Yu et al.proposed a reusable quantum signature scheme [Yu,Guo and Lin (2014)].In 2015,Wang et al.introduced a quantum proxy group signature scheme based on five particle cluster states [Wang,Ma,Wang et al.(2015)].In 2016,Luo et al.proposed a quantum homomorphic signature based on bell-state measurement [Luo,Yang,She et al.(2016)].In 2018,Qin et al.put forward a batch quantum multi-proxy signature [Qin,Tang and Tso (2018)].

In summary,there are many achievements in quantum signature,including arbitration quantum signature,quantum group signature,quantum blind signature,and other special quantum signature scheme.Although many schemes are based on the same principle,quantum signature is bound to usher in new applications with the development of quantum communication and quantum communication network.

2.7 Quantum Bit Commitment (QBC)

Although there exist bit commitment protocols with unconditionally hiding and calculated binding,or protocols with calculated hiding and unconditionally binding [Naor,Ostrovsky,Venkatesan et al.(1998)],classical bit commitment protocols with known unconditional security are not possible.In the research of traditional bit commitment,the researchers achieved computationally secure commitment protocol based on some oneway functions or mathematical problems.

Since unconditional secure QKD protocol appears,some scholars turned to research on quantum bit commitment (QBC).They hoped that QBC can provide unconditional security.In 1990s,Scholars put forward some QBC protocols [Brassard and Crépeau (1991);Brassard,Crdpeau,Jozsa et al.(1993);Ardehafi (1995);Mayers (1996);Lo and Chau (1997)],one of the most famous is the QBC protocol (BCJL protocol [Brassard,Crdpeau,Jozsa et al.(1993)]) proposed by Brassard et al.[Ardehafi (1995)],which was claimed unconditionally secure at that time.However,Mayers proved that the BCJL protocol is not secure [Mayers (1996)].In 1997,Lo et al.proved that the previous QBC protocol does not have unconditional security [Lo and Chau (1997)].And almost at the same time,Mayers also proved that the general QBC protocol (including classical measurement and two-way communication) cannot be unconditional secure [Mayers (1997)].The non-existence theorem of unconditional secure QBC (i.e.,Mayers-Lo-Chau no-go theorem) is often referred to as the “regression” of quantum cryptography research.If based on a certain assumption,or limited to specific circumstances,or put a low security requirement,secure QBC will become possible,so the study of QBC has not been suspended because of the Mayers-Lo-Chau no-go theorem.In 1998,Salvail presented a secure QBC protocol based on the assumption that the sender Alice cannot perform joint measurement on n qubits [Salvail (1998)].In 1999 and 2005,Kent introduced two bits commitment protocols to resist the attacks of quantum computer based on special relativity (RBC1 protocol [Kent (1999)] and RBC2 protocol [Kent (2005)]).In 2004,Hardy et al.presented an unconditionally secure QBC protocol with deception sensitivity [Hardy and Kent (2004)].In this protocol,if the committed or promised party is trying to cheat,the other party can detect such deceptive behavior by non-zero probability.Damgard et al.proposed two secure QBC protocols based on finite storage model in 2005 and 2007 respectively [Damgard,Fehr,Salvail et al.(2005);Damgard,Fehr,Renner et al.(2007)].In 2009,Choi et al.proposed secure non-static QBC protocol based on the trusted third party (TTP) [Choi,Hong,Chang et al.(2009)].In 2011,Chailloux et al.put forward QBC scheme with optimal boundary [Chailloux and Kerenidis (2011)].In 2012,Danan et al.proposed a practical QBC protocol [Danan and Vaidman (2012)].In 2013,Lunghi et al.carried out the experiment of bit commitment successfully based on quantum communication and special relativity [Lunghi,Kaniewski,Bussières et al.(2013)].In 2014,Pan's team realized unconditional secure bit commitment experiment [Liu,Cao,Curty et al.(2014)],which solved the problem of establishing trust between the distrust communication terminals.The experiment is evaluated as an important progress in cryptography and a pioneer in QBC experiment.In 2015,Adlam et al.proposed a relative QBC scheme independent of the device [Adlam and Kent (2015)].In 2016,Almeida et al.put forward a two-state QBC protocol in optical fiber [lmeida,Stojanovic,Paunković et al.(2016)].In 2018,Song et al.proposed a practical quantum bit commitment protocol based on quantum oblivious transfer [Song and Yang (2018)].

As the basis of designing many other quantum secure protocols,such as quantum coin flipping protocol and secure multi-party quantum computation,QBC protocol plays an important role in quantum secure communication,which will be a hot spot in this field.

2.8 Quantum coin tossing (QCT)

The coin tossing protocol is one of the basic cryptographic primitives,and it establishes a random bit between two users which are isolated in space and distrust mutually.In 1981,Blum proposed the first coin tossing protocol by using the classic password [Blum (1981)].In 1984,Bennett et al.extended the idea of throwing coins into the quantum field,and proposed a quantum coin tossing protocol known as the “BB84 protocol” [Aharonov,Ta-Shma,Vazirani et al.(2000)],which is different from the “BB84” protocol in QKD.In the next 10 years,the development of quantum coin tossing is relatively slow,the main reason is that the quantum coin tossing faces this controversy:Whether quantum coin tossing has unconditional security just like QKD? Until 1997,Mayers proved mathematically that the perfect quantum bit commitment (equivalent to quantum coin tossing) does not exist [Mayers (1997)],quantum coin tossing got the attention of researchers gradually.In 1998,Lo et al.gave the security proof of nonexisting absolute secure coin tossing protocol [Lo and Chau (1997)],but at the same time they also pointed out that the quantum coin tossing is still more secure than the classic one.This is why the researchers did not break the study of quantum coin tossing.In 2000,Aharonov et al.took the “BB84 protocol” as a template,and proposed a quantum coin tossing protocol based on quantum bit contract protocol (ATVY protocol) [Aharonov,Ta-Shma,Vazirani et al.(2000)],in which the preference probability was 0.354.In 2004,Ambainis designed a quantum coin tossing protocol based on the multi-band quantum symbols [Ambainis (2004)],in which the preference probability was reduced to 0.25.In the same year,Ambainis et al.proposed a multi-party quantum coin tossing protocol [Ambainis,Buhrman,Dodis et al.(2004)].In 2005,Mochon designed a new quantum coin tossing protocol,in which the preference probability was reduced to 0.192 [Mochon (2005)].In 2007,Kitaev et al.proved that the preference probability of quantum coin tossing can be reduced to 0.21 by using semi linear programming theory [Kitaev and Witte (2007)].In 2009,Chailloux et al.constructed a new protocol with preference probability of 0.21 by using the classical method based on the Mochon protocol [Chailloux and Kerenidis (2009)],which verified the conclusion of Kitaev.In the same year,Ganz designed a quantum voting protocol by using quantum coin tossing [Ganz (2009)].

In recent years,quantum coin tossing protocols have been extended to new applications.In 2011,Liu et al.proposed a novel quantum coin tossing protocol with computational security [Liu and Cao (2011)].In 2012,Ahlbrecht et al.introduced a quantum coin tossing scheme with asymptotic behavior [Ahlbrecht,Cedzich,Matjeschk et al.(2012)].In 2014,Ren et al.proposed a novel quantum coin toss scheme in the coin toss game [Ren,Wang,Lian et al.(2014)].In 2015,Zhao et al.put forward measurement-deviceindependent quantum coin toss protocol [Zhao,Yin,Wang et al.(2015)].In 2018,Abergel David proposed a quantum coin toss [Abergel (2018)].

With the development of quantum communication and network,we believe that the quantum coin toss protocol will have broad applications in the near future.

2.9 Quantum oblivious transfer (QOT)

As an important basis of quantum secure two-party computations,quantum oblivious transfer (QOT) has received much attention.In 1992,Yao et al.proposed a QOT protocol based on quantum bit commitment [Bennett,Brasssard,Crépeau et al.(1991)].In 2006,He et al.proposed a quantum secret all-or-non oblivious transfer protocol based on quantum entanglement [He and Wang (2003)].The security proof is given and the non-equivalence(?) of quantum secret all-or-non oblivious transfer protocol and quantum two-take-one oblivious transfer protocol is proved [He and Wang (2006)].In 2007,Colbeck et al.further studied the five conditions security of the two-party classic calculation,which showed that there was no unconditional secure classical calculation and illustrated the transmission results through quantum oblivious transfer [Colbeck (2007)].In the same year,Huang et al.put forward a QOT protocol by using the quantum positive operator [Yang,Huang,Yao et al.(2007)].In addition,some scholars studied quantum oblivious transfer in theory [Chen,Huang,Li et al.(2008);Schaffner (2010);Sikora (2012);Chailloux,Kerenidis and Sikora (2013);Yang,Yang,Lei et al.(2015)] and experiment [Fattal,Fiorentino,Chefles et al.(2008);Li,Wen,Qin et al.(2014);Nagy and Nagy (2017)].

2.10 Secure multi-party quantum computation (SMQC)

Secure multi-party computation (SMC) is the theoretical basis of distributed cryptography and also a key problem in distributed computing.Since 1982,Yao (Turing Award winner) proposed secure multi-party computation [Yao (1982)],which has attracted much attention now.At present,SMC based on mathematical complexity has made great progress in theory and application.However,these methods are based on the computational complexity and are computationally secure.With the rapid development of quantum information technology,the security of classical cryptography algorithm based on complexity theory has been seriously challenged.Secure quantum multiparty computation is a new hotspot,which combines quantum information technology and SMC.

In 2002,Crépeau et al.proposed the concept of SMQC and studied it systematically [Crépeau,Gottesam and Smith (2002)].Crépeau not only extended the classical SMC problem to SMQC,but also constructed a SMQC protocol based on quantum secret sharing protocol,which can tolerate any t (＜n/6) trickers.In 2006,Ben-Or et al.proposed a verifiable SMQC scheme based on approximate quantum error correction codes and quantum authentication schemes [Ben-Or,Crépeau,Gottesman et al.(2006)],which can tolerate [(n-1)/2] trickers.However,there are still some problems in these schemes.First,each participant must own a quantum state,however,it is not easy to be applied in practice because of the quantum coherence.Second,these SMQC schemes are only applicable to static fraud,and not to the case of adaptive fraud,for example they should determine which participants are not honest prior to the start of the protocol,which does not apply to the actual application of the dynamic changes of frauds.Finally,the SMQC protocol given by Crépeau et al.is just a few formal definitions,which defined the quantum security calculation with trusted third party in the ideal environment.However,in practical applications,the trusted third party does not virtually exist.Therefore,it is not efficient to implement secure multi-party quantum computation for special applications.In spite of this,some scholars have been concerned about this in recent years.In 2010,Loukopoulos et al.proposed a SMQC scheme in a dishonest environment by using quantum entanglement [Loukopoulos and Browne (2010)],which can tolerate [n/2] trickers.In 2013,Li et al.improved the SMQC protocol,which improves the efficiency of protocol [Li,Wen,Qin et al.(2013)].

According to the analyses made above,the research focused on the characteristics of basic SMQC protocol still has a certain distance from the practical application.To solve these problems,some SMQC protocols for special applications have been proposed,such as quantum anonymous communication protocol [Wang,Wen and Zhu (2010)],blind quantum computing protocol [Broadbent,Fitzsimons and Kashefi (2009);Shi,Mu,Zhong et al.(2016)],quantum voting protocol [Li and Zeng (2008)] and quantum auction protocol [Hogg,Harsha and Chen (2007)].

Compared with the classical SMC,due to the unique characteristics of quantum information,SMQC shows great advantages in security,robustness and communication efficiency,especially in eavesdropping detection.

3 Research on quantum communication network

Since the mode of point-to-point quantum communication cannot meet the requirements of practical application.Quantum communication network is proposed to provide secure communication services for more users with limited resources,and the global wide area quantum communication network is in research at present.

In 2002,the United States began to design DARPA quantum key distribution network,and built a six-node quantum network [Elliott,Colvin,Pearson et al.(2005)] by 2004.In 2007,BBN proposed establishing the national quantum communication network via

satellite connection [Ma,Mink and Tang (2009)].In 2012,Alamos Los laboratory successfully demonstrated the application of quantum communication in the national grid [Zhou,Lu,Lei et al.(2014)].In 2013,the Alamos Los laboratory established a quantum communication network using time division multiplexing,and proposed to build intercity quantum network [Richard,Jane,Kevin et al.(2013)].In the same year,NASA successfully launched the PhoneSat satellite,and they intended to establish a global quantum communication network [Haque,Teel,Tintore et al.(2014)].In Europe,in 2004,Austria began to build SECOQC (secure communication based on quantum cryptography) [Ma,Mink and Tang (2009)].In 2008,the QKD SECOQC network of five nodes was confirmed experimentally in Vienna.In 2008,the Space-QUEST program of European Space Agency deployed entangled light in the international space station,the test distance of which went beyond that on the ground with several orders of magnitude [Poppe,Peev and Maurhart (2008)].In 2009,quantum metropolitan area network in Geneva started running [Ursin,Jennewein,Kofler et al.(2009)].The Metro quantum communication network test bed was built in Spain and which was integrated into the existing optical communication network [Stucki,Legré,Buntschu et al.(2011)].In 2009,South Africa launched the Durban quantum city program [Lancho,Martinez,Elkoussl et al.(2010)],and completed the deployment of quantum network in the same year.In 2009,Thailand launched quantum communication network construction with a period of 3 years [Mirza and Petruccione (2010)].In 2010,the Japanese NICT built a 45 Km long quantum communication network in Tokyo [Yin,Ren,Lu et al.(2012)].Australia built a quantum network in its capital (Canberra),and built the ground and space quantum network cooperating with the NASA/JPL [Pattaranantakul,Janthong,Sanguannam et al.(2012)].In 2012,Singapore plans to launch a small cube satellite carrying entangled photon source [Sharma (2012)].Jennewein Thomas group in Canada designed quantum satellite,and the feasibility of the experiment is assessed [Ling (2012)].In China,Guo's team achieved four-user quantum optical fiber network [Tang,Ma,Mink et al.(2008)] in 2007.In 2008,Pan's group set up a light quantum telephone network with 20 Km [Chen,Han,Zhang et al.(2009)].In 2009,the Pan's team developed a star quantum communication network with five nodes,in which the distance between each node is about 8 Km-60 Km [Chen,Liang,Liu et al.(2009)].In the same year,Guo's team built a multi-level quantum government network [Chen,Wang,Liang et al.(2010)].In 2011,Pan's team organized the strategic pilot project of Chinese Academy of Sciences (quantum science test satellite),and planned to launch the first quantum communication satellite in the world around 2016 [Wang,Chen,Yin et al.(2010)].In 2012,the 170 Km quantum communication network is built in Beijing,which was the first financial quantum communication network applications in the world (including four nodes and three users) [Li,Liao,Chen et al.(2014)].In 2013,quantum communication test network in Jinan (including 50 nodes and 90 users) put into operation [Wu,Yu,Zhao et al.(2014)].In 2014,the Beijing-Shanghai route project went through the demonstration,which has been delivered in 2016 [Wei,Liu,Sun et al.(2018)],and an intercontinental quantum communication network linking Asia and Europe is planned to be built in 2020.A global quantum wide area network is to be built in 2030,and the structure diagram of quantum wide area network is shown in Fig.1.

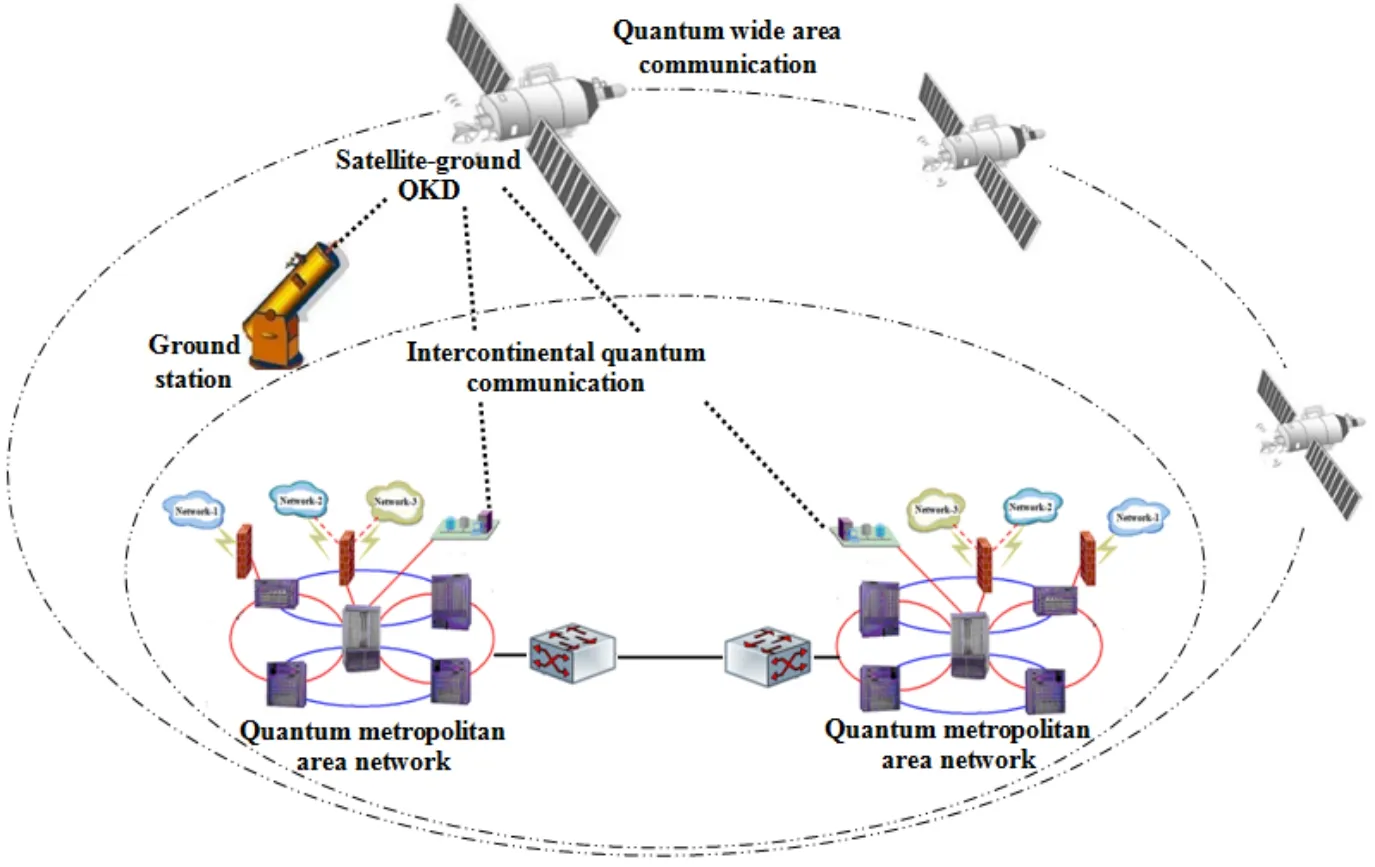
Figure 1:The structure diagram of quantum wide area network

4 Analysis on research progress of quantum communication and trust management

4.1 Research progress of quantum communication and quantum communication network

From the analysis of the previous results,the theory and technology of quantum communication and quantum communication network are mainly developed in two directions,namely,the vertical and the horizontal.In the horizontal,except to quantum key distribution (QKD),quantum teleportation (QT),quantum secret sharing (QSS),quantum secure direct communication (QSDC),quantum identity authentication (QIA),quantum signature (QS),quantum bit commitment (QBC),quantum coin tossing (QCT),quantum oblivious transfer (QOT),secure multiparty quantum computation (SMQC) and other theories and technologies had appeared.There are some classical theories and technologies corresponding to these quantum theories and technologies,and the security of which are much higher than the classical ones.In the longitudinal direction,there are quantum secure communication protocol,long-distance quantum communication,quantum communication network and so on.

Although theories and techniques of quantum communication have been developed,most of them are based on the study of point-to-point one-way system.The communication network in reality is one-to-many or many-to-many network system.To make quantum communication and quantum communication network practical,not only to achieve point-to-point communication (as shown in Fig.2),it is more important to realize the network communication between between multiple users,that is,the network of quantum communication is needed.

Figure 2:Point-to-point QKD communication system

4.2 Research of trust management in quantum communication network

To make quantum communication and quantum communication network practical,to expand the application and improve the distance of quantum communication,it is urgent to establish a secure and reliable quantum communication network to meet the needs of multi-user communication.Fig.3 is the structure diagram of quantum communication network with trusted third party (TTP).

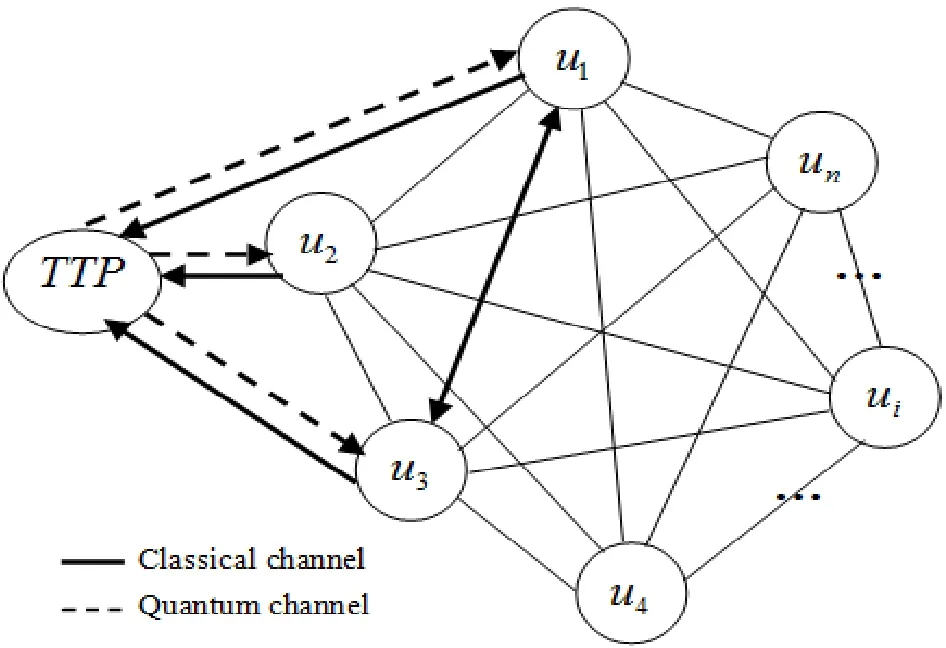
Figure 3:The structure diagram of quantum communication network with TTP (Note:thinking of the network structure graph clarity,this figure only marks the connection between TTP,1u,2u,3u and 4u)

In Fig.3,we assume that node3u wants to communicate with node1u,but3u does not know whether1u is credible or not.To prevent himself from being cheated by1u,3u gets some information which can evaluate the trust degree of1u from TTP.Then3u calculates the trust value of1u according to the information provided by TTP.3u judges whether1u is credible according to the trust value he calculated.

Like classical networks,trust problem is the premise and foundation of quantum secure communication and trust cannot simply be attributed to security issues,the basic and importance of trust management in quantum communication networks should be seen.How to ensure the reliability of each node (user) in the quantum communication network and prevent counterfeiting,tampering,hacking,denial and deception,is the key to ensure the practical and network of quantum communication.Therefore,the research of quantum trust management model in the quantum communication network will become a hotspot.Although some scholars have concerned about the trust of quantum communication and trust management model in the quantum communication network environment,however,compared with other theories and techniques of quantum communication,the results of trust and trust management model of quantum communication are very few,which is still in its initial stage.At present,the existing results mainly involves trust modeling (quantitative description of each trust factor),trust establishment (assessment),node behavior management,multi-user quantum secure communication and secret information sharing.

4.2.1 Trust management modeling in quantum communication network

The results about quantum trust modeling is few.Liu et al.[Liu and Li (2012)] proposed a quantum trust management model based on social network.Zhou [Zhou (2012)] studied the trust network in quantum communication.Pattaranantakul et al.[Pattaranantakul,Sanguannam,Sangwongngam et al.(2015)] proposed a Key Management Protocol for Secure RTMP Video Streaming toward Trusted Quantum Network.However,in Zhou et al.[Zhou (2012);Liu and Li (2012);Pattaranantakul,Sanguannam,Sangwongngam et al.(2015)],the probability of a one-time success in quantum communication between nodes was used as the node trust (and as a model),not considering the fuzzy characteristics of the factors that affect the node trust in the quantum communication network environment.In previous studies,they are found that the quantum communication network is similar with the classical communication network:there are many factors that are related to node trust in quantum communication networks,such as the historical reputation of nodes,the probability of a one-time success in quantum communication,the identity of node,the location of the node.These trust factors have the characteristics of randomness,subjectivity and diversity,which are mainly fuzzy.The main difficulty in study of trust lies in how to make a quantitative and accurate description of fuzziness.

4.2.2 The evaluation of trust in quantum communication network environment

About the evaluation of trust,the results are mainly focused on quantum identity authentication (In fact,two sides in one communication have established some trust between each other after the identity authentication),quantum bit commitment and trust evaluation (to decide whether a node is trustable or not by evaluating the trust degree of the node).In the study of quantum identity authentication,a (T,n) threshold authentication scheme based on GHZ was put forward in Yang et al.[Yang,Wang,Jia et al.(2013)].A quantum identity authentication scheme without entanglement was studied based on the “ping pong” technique in Yuan et al.[Yuan,Liu,Pan et al.(2014)].About the study of quantum bit commitment,Lunghi et al.[Lunghi,Kaniewski,Bussières et al.(2013)] studied the quantum bit commitment experiment based on quantum communication and special relativity,which established trust directly between the two parties,Liu et al.[Liu,Cao,Curty et al.(2014)] achieved a unconditional secure “bit commitment” experiment,and solved the problem of how to establish trust between distrustful terminals,which was a major breakthrough and was evaluated as an important progress in cryptography and a pioneer in experiment in this field.As for the study of quantum trust evaluation,Zhou et al.[Zhou (2012);Liu and Li (2012)] characterized the degree of trust between nodes by using the communication quality (the one-time success probability of quantum communication among nodes),based on which the trust of node was evaluated.Zhang et al.[Zhang,Xie,Yin et al.(2017)] discussed how to improve the security of information transferring between trusted nodes by studying the trusted node model.However,Yang et al.[Yang,Wang,Jia et al.(2013);Yuan,Liu,Pan et al.(2014);Zhandry (2012);Ma,Huang,Bao et al.(2016);Zawadzki (2019);Lunghi,Kaniewski,Bussières et al.(2013);Liu,Cao,Curty et al.(2014)] established trust directly between the two parties by using quantum identity authentication and quantum bit commitment,trust in multi-user environment was not taken into account.Zhou et al.[Zhou (2012);Liu and Li (2012);Pattaranantakul,Sanguannam,Sangwongngam et al.(2015);Peter and Stefan (2009)] evaluated the node trust only with the one-time success probability of quantum communication (or decide whether to establish a trust between nodes),how to safely evaluate the trust in multi-user environment was not considered.Furthermore,multiple factors were not considered that affect the trust of nodes,such as the historical reputation degree of nodes,the probability of successful communication,the identity information of nodes and the location of nodes.

4.2.3 The problem of node behavior management in quantum communication network

The results about node behavior management in quantum communication networks are few.Zhou et al.[Zhou (2012);Liu and Li (2012);Pattaranantakul,Sanguannam,Sangwongngam et al.(2015)] studied the behavior of quantum nodes by measuring whether the nodes achieving the desired requirements (such as the one-time success probability of a node).You et al.[You,Liu and Wang (2012)] proposed a optimization model of network resource allocation based on quantum behavior.However,in Zhou et al.[Zhou (2012);Liu and Li (2012);Pattaranantakul,Sanguannam,Sangwongngam et al.(2015);You,Liu and Wang (2012)],the behavior of nodes was studied through the success probability of communication between nodes,the possible existence of a variety of unsafe behavior in the network was not considered.In fact,similar with the condition in classical network,the node behavior in quantum communication network can be expected,managed and evaluated.

4.2.4 The problem of multi-user quantum secure communication and secret information sharing

There have been many results about multi-user quantum secure communication and secret information sharing.In the study of multi-user quantum secure communication,Fröhlich et al.[Fröhlich,Dynes,Lucamarini et al.(2013)] proposed a quantum access network (a network node can share the key exchange with 64 users).Chang et al.[Chang,Jin,Jong et al.(2012)] proposed a multi-user quantum network system based on X-type entangled state.Salvail et al.[Salvail,Momtchil,Eleni et al.(2010)] studied a trusted relay QKD network (to ensure the authenticity and privacy of a key).Sun et al.[Sun,Cheng and Ji (2014)] studied a trusted relay QKD network with differentiated services.David et al.[David,Jesus,Alex et al.(2013)] proposed a secure optical network based on QKD and weakly trusted relay.Lin et al.[Lin,Huang and Liu (2013)] put forward a multi-user QKD scheme based on mutual authentication and Bell state.William et al.[William,Razieh,Ma et al.(2015)] introduced a QKD scheme based on trusted relay node.About the study of multi-user secret information sharing,Zhang et al.[Zhang,Liu and Li (2011)] proposed a quantum secret sharing (QSS) scheme based on error correcting code.Sun et al.[Sun,Xu,Chen et al.(2013)] presented a scalable QSS network.Bell et al.[Bell,Markham,Wadsworth et al.(2014)] demonstrated the experiment of QSS based on graph state.Li et al.[Li,Long,Chan et al.(2011)] presented a secret sharing scheme without a trusted party.Wang et al.[Wang,Zou and Zhao (2014)] proposed a QSS scheme with secure and trusted center.Li et al.[Li,Zubairy and Al-Amri (2018)] proposed a scheme of quantum Secure Group Communication.However,these studies mentioned above are mainly from the perspective of expanding the number of users.In fact,similar with classical network,to fulfill quantum communication network and practical,ensuring network security and normal operation is one of the most important tasks,except to expand the node (user) scale.To ensure the normal operation and security of multi-user quantum network,the identity and behavior of nodes waiting for accessing the network should be authenticated and controlled effectively.

In summary,the research results mentioned above laid the foundation for the research of secure and reliable quantum communication network.But these achievements promoted the practical and networking of quantum communication,either establishing trust between two sides of communication through quantum identity authentication or quantum bit commitment,either evaluating the trust of node with the success probability of quantum communication,or achieving multi-user quantum communication and secret information sharing by expanding the amount of users.Multiple factors and the fuzzy features of these factors are not considered,which affect the trust of nodes,such as the historical reputation degree of nodes,the probability of successful communication,the identity information of nodes and the location of nodes.In multi-user quantum communication network,how to evaluate the trust of nodes securely,how to manage node behavior trustedly and how to access node in network trustedly are not considered.Therefore,it is of great significance for the research of trust management and trust management model in quantum communication network,which is bound to promote the practical and networking of quantum communication,and it will be a research hotspot in establishing secure and reliable quantum communication network.

5 Conclusions

Quantum communication is a new cross discipline combining classical information theory and quantum mechanics,which using quantum state to carry information.Quantum communication is expected to break through the limit of classical communication technology in the aspects of communication security,computing power,information transmission,channel capacity and measurement accuracy,which has become a new direction and will be the mainstream in the field of communication and information in twenty-first century.This paper summarized the research status of theory and technology in quantum communication and quantum communication network.The key technologies of establishing secure and reliable quantum communication networks are classified and summarized.The problems and trend of each direction in trust management of quantum communication network are discussed in depth.Therefore,it is of great significance to further develop the theory and application study of secure and reliable quantum communication networks.

Acknowledgement:This work is supported by the National Natural Science Foundation of China (No.61572086),the Innovation Team of Quantum Security Communication of Sichuan Province (No.17TD0009),the Academic and Technical Leaders Training Funding Support Projects of Sichuan Province (No.2016120080102643),the Application Foundation Project of Sichuan Province (No.2017JY0168).

References

Abergel,D.(2018):A quantum coin toss.Nature Physics,vol.14,no.1,pp.7-17.

Acín,A.;Gisin,N.;Masanes,L.(2006):From bell's theorem to secure quantum key distribution.https://arxiv.org/pdf/quant-ph/0510094.pdf.

Adlam,E.;Kent,A.(2015):Device-independent relativistic quantum bit commitment.https://arxiv.org/pdf/1504.00944.pdf.

Aharonov,D.;Ta-Shma,A.(2003):Adiabatic quantum state generation and statistical zero knowledge.Proceedings of the 35th Annual ACM Symposium on Theory of Computing,pp.20-29.

Aharonov,D.;Ta-Shma,A.;Vazirani,U.V.;Yao,A.C.(2000):Quantum bit escrow.Proceedings of the 32nd Annual ACM Symposium on Theory of Computing,pp.705-714.

Ahlbrecht,A.;Cedzich,C.;Matjeschk,R.;Scholz,V.B.;Werner,A.H.et al.(2012):Asymptotic behavior of quantum walks with spatio-temporal coin fluctuations.Quantum Information Processing,vol.11,no.5,pp.1219-1249.

Almeida,A.J.;Stojanovic,A.D.;Paunković,N.;Loura,R.;Muga,N.J.et al.(2016):Implementation of a two-state quantum bit commitment protocol in optical fibers.http://iopscience.iop.org/article/10.1088/2040-8978/18/1/015202.

Ambainis,A.(2004):A new protocol and lower bounds for quantum coin flipping.Journal of Computer and System Sciences,vol.68,no.2,pp.398-416.

Ambainis,A.;Buhrman,H.;Dodis,Y.;Roehrig,H.(2004):Multiparty quantum coin flip-ping.Proceedings of the 19th Annual IEEE Symposium on Computational Complexity,pp.250-260.

Ardehafi,M.(1995):A quantum bit commitment protocol based on EPR states.https://arxiv.org/pdf/quant-ph/9505019.pdf.

Bacco,D.;Christensen,J.B.;Castaneda,M.U.;Ding,Y.H.;Forchhammer,S.et al.(2016):Two-dimensional distributed-phase-reference protocol for quantum key distribution.https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5177871/pdf/srep36756.pdf.

Bai,C.M.;Li,Z.H.;Liu,C.J.;Li,Y.M.(2017):Quantum secret sharing using orthogonal multiqudit entangled states.https://link.springer.com/content/pdf/10.1007%2Fs11128-017-1739-z.pdf

Barrett,J.;Hardy,L.;Kent,A.(2005):No signaling and quantum key distribution.https://arxiv.org/pdf/quant-ph/0405101.pdf.

Bege,A.;Englert,B.G.;Kurtsiefer,C.;Weinfurter,H.(2002):Secure communication with a publicly known key.https://arxiv.org/pdf/quant-ph/0111106v2.pdf.

Bege,A.;Englert,B.G.;Kurtsiefer,C.;Weinfurter,H.(2002):Secure communication with single photon two qubit ststes.Journal of Physics A:Mathematical and General,vol.35,no.7,pp.407-413.

Bell,B.A.;Markham,D.;Herrera-Martí,D.A.;Marin,A.;Wadsworth,W.J.et al.(2014):Experimental demonstration of graph-state quantum secret sharing.https://www.nature.com/articles/ncomms6480.pdf.

Bennett,C.H.(1992):Quantum cryptography using any two no orthogonal states.Physical Review Letters,vol.68,no.21,pp.3121-3124.

Bennett,C.H.;Brassard,G.(1984):Quantum cryptography:public key distribution and coin tossing.Proceedings of the IEEE International Conference on Computers,Systems and Signal Processing,pp.175-179.

Bennett,C.H.;Brassard,G.;Crépeau,C.;Jozsa,R.;Peres,A.et al.(1993):Teleporting an unknown quantum state via dual classical and einstein-podolsky-rosen channels.Physical Review Letters,vol.70,no.13,pp.1895-1899.

Bennett,C.H.;Brasssard,G.;Crépeau,C.;Skubiszewska,M.H.(1991):Pratical quantum oblivious transfer.Lecture Notes in Computer Science,vol.576,no.12,pp.351-366.

Ben-Or,M.;Crépeau,C.;Gottesman,D.;Hassidim,A.;Smith,A.(2006):Secure multiparty quantum computation with (only) a strict honest majority.Proceedings of the 47th Annual IEEE Symposium on Foundations of Computer Science,pp.249-260.

Blum,M.(1981):Coin flipping by telephone:a protocol for solving impossible problems.Advances in Cryptology:A Report on Crypto'81,pp.11-15.

Bostrom,K.;Felbinger,T.(2002):Deterministic secure direct communication using entanglement.https://arxiv.org/pdf/quant-ph/0209040v2.pdf.

Boyer,M.;Kenigsberg,D.;Mor,T.(2007):Quantum key distribution with classical bob.https://arxiv.org/pdf/quant-ph/0703107.pdf.

Brassard,G.;Crépeau,C.(1991):Quantum bit commitment and coin tossing protocols.Advances in Cryptology Proceedings of Crypto'90,pp.49-61.

Brassard,G.;Crépeau,C.;Jozsa,R.;Langlois,D.(1993):A quantum bit commitment scheme provably unbreakable by both parties.Proceedings of the 34th Annual IEEE Symposium on Foundations of Computer Science,pp.362-371.

Broadbent,A.;Fitzsimons,J.;Kashefi,E.(2009):Universal blind quantum computation.Proceedings of the 50th Annual IEEE Symposium on Foundations of Computer Science,pp.517-526.

Buttler,W.T.;Hughes,R.J.;Lamoreaux,S.K.;Morgan,G.L.;Nordholt,J.E.(2000):Daylight quantum key distribution over 1.6 km.Physical Review Letters,vol.84,no.24,pp.5652-5655.

Chang,H.H.;Jin,O.H.;Jong,I.L.;Yang,H.J.(2012):Multi-user quantum network system and quantum communication using χ-type entangled states.Journal of the Korean Physical Society,vol.61,no.1,pp.1-5.

Chailloux,A.;Kerenidis,I.(2011):Optimal bounds for quantum bit commitment.Proceedings of the 52nd IEEE Annual Symposium on Foundations of Computer Science,pp.354-362.

Chailloux,A.;Kerenidis,I.;Sikora,J.(2013):Lower bounds for quantum oblivious transfer.Quantum Information ＆ Computation,vol.13,no.1-2,pp.158-177.

Chailloux,A.;Kerenidis,I.(2009):Optimal quantum strong coin flipping.Proceedings of 50th Annual IEEE Symposium on the Foundations of Computer Science,pp.527-538.

Chang,Y.;Xu,C.X.;Zhang,S.B.;Yan,L.L.(2013):Quantum secure direct communication and authentication protocol with single photons.Chinese Science Bulletin,vol.58,no.36,pp.4571-4576.

Chen,I.C.;Huang,T.;Li,C.M.(2008):Efficient one-out-of-two quantum oblivious transfer based on four-coherent-state postselection protocol.http://iopscience.iop.org/article/10.1088/0031-8949/78/03/035005/pdf.

Chen,T.Y.;Liang,H.;Liu,Y.;Cai,W.Q.;Ju,L.et al.(2009):Field test of a practical secure communication network with decoy-state quantum cryptography.Optics Express,vol.17,no.8,pp.6540-6549.

Chen,T.Y.;Wang,J.;Liang,H.;Liu,W.Y.;Liu,Y.et al.(2010):Metropolitan allpass and inter-cityquantum communication network.Optics Express,vol.18,no.26,pp.27217-27225.

Chen,W.;Han,Z.F.;Zhang,T.;Wen,H.;Yin,Z.Q.et al.(2009):Field experiment on a “star type” metropolitan quantum key distribution network.IEEE Photonics Technology Letters,vol.21,no.9,pp.575-577.

Choi,J.W.;Hong,D.;Chang,K.Y.;Chi,D.P.;Lee,S.(2009):Is quantum bit commitment really impossible? Proceedings of the 9th Asian Conference on Quantum Information Science,pp.205-206.

Cleve,R.;Gottesman,D.;Lo,H.K.(1999):How to share a quantum secret.Physical Review Letters,vol.83,no.3,pp.648-651.

Colbeck,R.(2007):The impossibility of secure two-party classical computation.https://arxiv.org/pdf/0708.2843.pdf.

Crépeau,C.;Gottesam,D.;Smith,A.(2002):Secure multi-party quantum computation.Proceedings of the 34th Annual ACM Symposium on Theory of Computing,pp.643-652.

Damgard,I.B.;Fehr,S.;Renner,R.;Salvail,L.;Schaffner,C.(2007):A tight highorder entropic quantum uncertainty relation with applications.Advances in Cryptology Proceedings of Crypto'07,pp.360-378.

Damgard,I.B.;Fehr,S.;Salvail,L.;Schaffner,C.(2005):Cryptography in the bounded quantum-storage model.Proceedings of the 46th Annual IEEE Symposium on Foundations of Computer Science,pp.449-458.

Danan,A.;Vaidman,L.(2012):Practical quantum bit commitment protocol.Quantum Information Processing,vol.11,no.3,pp.769-775.

David,E.;Jesus,M.M.;Alex,C.et al.(2013):Secure optical networks based on quantum key distribution and weakly trusted repeaters.Journal of Optical Communications and Networking,vol.5,no.4,pp.316-328.

Davidovich,L.;Zagury,N.;Brune,Μ.;Raimond,J.M.;Haroche,S.et al.(1994):Teleportation of an atomic state between two cavities using nonlocal microwave fields.Physical Review A,vol.50,no.2,pp.895-898.

Deng,F.G.;Long,G.L.(2004):Secure direct communication protocol with a quantum one-time-pad.https://arxiv.org/pdf/quant-ph/0405177v1.pdf.

Deng,F.G.;Long,G.L.;Liu,X.S.(2003):A two-step quantum direct communication protocol using the einstein-podolsky-rosen pair block.https://arxiv.org/pdf/quant-ph/0308173v1.pdf.

Deng,F.G.;Yan,F.L.;Li,X.H.;Li,C.Y.;Zhou,H.Y.et al.(2005):Addendum to “quantum secret sharing between multiparty and multiparty without entanglement”.https://arxiv.org/pdf/quant-ph/0508171.pdf.

Dong,L.;Xiu,X.M.;Gao,Y.J.(2007):Multiparty quantum state sharing of m-qubit state.International Journal of Modern Physics C,vol.18,no.11,pp.1699-1706.

Dusek,M.;Haderka,O.;Hendrych,M.;Myska,R.(1999):Quantum identification system.Physical Review A,vol.60,no.1,pp.149-156.

Ekert,A.K.(1991):Quantum cryptography based on bell's theorem.Physical Review Letters,vol.67,no.6,pp.661- 663.

Elliott,C.;Colvin,A.;Pearson,D.;Pikalo,O.;Schlafer,J.et al.(2005):Current status of the DARPA quantum network.Quantum Information and Computation III (Proceeding of SPIE),vol.5815,no.1,pp.138-149.

Fattal,D.;Fiorentino,M.;Chefles,A.;Beausoleil,R.(2008):Experiment realization of quantum oblivious transfer.Conference on Laser and Electro Optics/Quantum Electronics and Laser Science Conference,pp.235-243.

Ferreira da Silva,T.;Vitoreti,D.;Xavier,G.B.;Temporäo,G.P.;von der Weid,J.P.(2013):Proof-of-principle demonstration of measurement device independent quantum key distribution using polarization qubits.https://arxiv.org/ftp/arxiv/papers/1207/1207.6345.pdf

Fröhlich,B.;Dynes,J.F.;Lucamarini,M.;Lucamarini,M.;Sharpe,A.W.et al.(2013):A quantum access network.Nature,vol.501,no.7465,pp.69-73.

Ganz,M.(2009):Quantum leader election.https://link.springer.com/content/pdf/10.1007%2Fs11128-017-1528-8.pdf.

Gao,F.;Qin,S.J.;Guo,F.Z.;Wen,Q.Y.(2011):Cryptanalysis of quantum secure direct communication and authentication scheme via bell states.http://cpl.iphy.ac.cn/10.1088/0256-307X/28/2/020303.

Gao,T.;Yan,F.L.;Li,Y.C.(2009):Quantum secret sharing between m-party and nparty with six states.Science in China Series G:Physics,Mechanics ＆ Astronomy,vol.52,no.8,pp.1191-1202.

Gottesman,D.;Chuang,I.L.(2001):Quantum digital signatures.https://arxiv.org/pdf/quant-ph/0105032.pdf

Guo,G.C.(2008):The rise and development of quantum information science in the university of science and technology of China.Physics,vol.37,no.8,pp.556-561 (In Chinese).

Guo,G.P.;Guo,G.C.(2003):Quantum secret sharing without entanglement.Physics Letters A,vol.310,no.4,pp.247-251.

Gurty,M.;Santors,D.J.(2001):Quantum authentication of classical messages.https://arxiv.org/pdf/quant-ph/0103122v2.pdf.

Hänggi,E.;Renner,R.;Wolf,S.(2010):Efficient device-independent quantum key distribution.International Conference on Advances in Cryptology-eurocrypt 2010,Lecture Notes in Computer Science,pp.216-234.

Haque,S.E.;Teel,G.;Tintore,O.;Trinh,T.;Uribe,E.et al.(2014):Applications of micro-cathode arc thruster as in-space propulsion subsystem for phonesat.IEEE Aerospace Conference Proceedings,pp.1-18.

Hardy,L.;Kent,A.(1999):Cheat sensitive quantum bit commitment.https://arxiv.org/pdf/quant-ph/9911043.pdf.

He,G.P.;Wang,Z.D.(2003):Oblivious transfer using quantum entanglement.Physical Review A,vol.73,no.1,pp.2518-2521.

He,G.P.;Wang,Z.D.(2006):Nonequivalence of two flavors of oblivious transfer at the quantum level.https://journals.aps.org/pra/abstract/10.1103/PhysRevA.73.044304.

Hillery,M.;Buzek,V.;Berthiaume,A.(1999):Quantum secret sharing.Physical Review A,vol.59,no.3,pp.1829-1834.

Hogg,T.;Harsha,P.;Chen,K.Y.(2007):Quantum auctions.International Journal of Quantum Information,vol.5,no.12,pp.751-760.

Huo,M.R.;Qin,J.L.;Cheng,J.L.;Yan,Z.H.;Qin,Z.Z.et al.(2018):Deterministic quantum teleportation through fiber channels.http://advances.sciencemag.org/content/advances/4/10/eaas9401.full.pdf.

Jennewein,T.;Simon,C.;Weihs,G.;Weinfurter,H.;Zeilinger,A.(2000):Quantum cryptography with entangled photons.Physical Review Letters,vol.84,no.20,pp.4729-4732.

Karimipour,V.;Asoudeh,M.(2015):Quantum secret sharing and random hopping:using single states instead of entanglement.https://arxiv.org/pdf/1506.02966.pdf.

Karlsson,A.;Koashi,M.;Imoto,N.(1999):Quantum entanglement for secret sharing and secret splitting.Physical Review A,vol.59,no.1,pp.162-168.

Kent,A.(1999):Unconditionally secure bit commitment.Physical Review Letters,vol.83,no.7,pp.1447-1450.

Kent,A.(2005):Secure classical bit commitment using fixed capacity communication channels.Journal of Cryptology,vol.18,no.11,pp.313-335.

Kim,Y.H.;Kulik,S.P.;Shih,Y.H.(2001):Quantum teleportation of a polarization state with a complete bell state measurement.Physical Review Letters,vol.86,no.7,pp.1370-1373.

Kitaev,A.V.;Witte,N.S.(2007):Boundary conditions for scaled random matrix ensembles in the bulk of the spectrum.Journal of Physics A:Mathematical and Theoretical,vol.40,no.42,pp.12725-12740.

Knoll,L.T.;Schmiegelow,C.T.;Larotonda,M.A.(2014):Noisy quantum teleportation:an experimental study on the influence of local environments.https://arxiv.org/pdf/1410.5771.pdf.

Kurtsiefer,C.;Zarda,P.;Halder,M.;Weinfurter,H.;Gorman,P.M.et al.(2002):A step towards global key distribution.https://www.nature.com/articles/419450a.

Lancho,D.;Martinez,J.;Elkoussl,D.;Soto,M.;Martin,V.(2010):QKD in standard optical telecommunications networks.International Conference on Quantum Comunication and Quantum Networking,pp.142-149.

Lee,H.;Hong,C.;Kim,H.;Lim,J.;Yang,H.J.(2004):Arbitrated quantum signature scheme with message recovery.Physics Letters A,vol.321,no.5,pp.295-300.

Lee,H.;Lim,J.;Yang.H.J.(2005):Quantum direct communication with authentication.https://arxiv.org/pdf/quant-ph/0512051v1.pdf.

Li,G.;Ye,M.Y.;Lin,X.M.(2013):Entanglement fidelity of the standard quantum teleportation channel.Physics Letters A,vol.377,no.23-24,pp.1531-1533.

Li,Q.;Long,D.Y.;Chan,W.H.;Qiu,D.W.(2011):Sharing a quantum secret without a trusted party.Quantum Physics,vol.10,no.1,pp.97-106.

Li,W.L.;Li,C.F.;Guo,G.C.(2000):Probabilistic teleportation and entanglement matching.https://arxiv.org/pdf/quant-ph/9910021.pdf.

Li,Y.;Liao,S.K.;Chen,X.L.;Chen,W.;Cheng,K.et al.(2014):Space-bound optical source for satellite-ground decoy-state quantum key distribution.Optics Express,vol.22,no.5,pp.27281-27289.

Li,Y.;Zeng,G.H.(2008):Quantum anonymous voting system based on entangled state.Optical Review,vol.15,no.5,pp.219-223.

Li,Y.B.;Wen,Q.Y.;Qin,S.J.(2013):Improved secure multiparty computation with a dishonest majority via quantum means.International Journal of Theoetical Physics,vol.52,no.1,pp.199-205.

Li,Y.B.;Wen,Q.Y.;Qin,S.J.;Guo,F.Z;Sun,Y.(2014):Practical quantum all-ornothing oblivious transfer protocol.Quantum Information Processing,vol.13,no.1,pp.131-139.

Li,Y.H.;Li,X.L.;Nie,L.P.(2015):Controlled quantum secure direct communication by using a five-atom cluster state in cavity QED.International Journal of Theoretical Physics,vol.54,vol.10,pp.3728-3732.

Li,Z.H.;Zubairy,M.S.;Al-Amri,M.(2018):Quantum secure group communication.https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5832868/pdf/41598_2018_Article_2174 3.pdf.

Lin,S.;Huang,C.;Liu,X.F.(2013):Multi-user quantum key distribution based on bell states with mutual authentication.http://iopscience.iop.org/article/10.1088/0031-8949/87/03/035008.

Ling,A.(2012):Entangled photon systems for small satellites.Report PPT at First NASA Quantum Future Technologies Conference,pp.216-223.

Liu,D.;Pei,C.X.;Quan,D.X.;Zhao,N.(2010):A new quantum secure direct communication scheme with authentication.http://cpl.iphy.ac.cn/Y2010/V27/I5/50306.

Liu,F.M.;Li,H.X.(2012):Social network-based quantum trust management.The 2nd International Conference on Computer Science and Network Technology,pp.487-490.

Liu,G.H.;Cao,D.(2011):A novel quantum coin tossing protocol with computationally secure.High Performance Networking,Computing and Communication Systems,vol.163,no.17,pp.350-353.

Liu,W.J.;Chen,H.W.;Li,Z.Q.;Liu,Z.H.;Xiao,F.Y.(2008):Efficient quantum secure direct communication with authentication.Chinese Physics Letters,vol.25,no.7,pp.2354-2357.

Liu,Y.;Cao,Y.;Curty,M.;Liao,S.K.;Wang,J.et al.(2014):Experimental unconditionally secure bit commitment.https://arxiv.org/pdf/1306.4413.pdf.

Ljunggren,D.;Bourennane,M.;Karlsson,A.(2000):Authority based user authentication in quantum key distribution.Physical Review A,vol.62,no.2,pp.299-302.

Lo,H.K.;Chau,H.F.(1997):Is quantum bit commitment really possible? Physical Review Letters,vol.78,no.17,pp.3410-3413.

Long,G.L.;Liu,X.S.(2002):Theoretically efficient high capacity quantum key distribution scheme.https://arxiv.org/pdf/quant-ph/0012056.pdf.

Loukopoulos,K.;Browne,D.(2010):Secure multiparty computation with a dishonest majority via quantum means.https://journals.aps.org/pra/abstract/10.1103/PhysRevA.81.062336.

Lü,X.;Feng,D.G.(2005):Quantum digital signature based on quantum one-way functions.Proceedings of the 7th International Conference on Advanced Communication Technology,pp.514-517.

Lucamarini,M.;Mancini,S.(2005):Secure deterministic communication without entanglement.https://arxiv.org/pdf/quant-ph/0405083v3.pdf.

Lunghi,T.;Kaniewski,J.;Bussières,F.;Houlmann,R.;Tomamichel,M.(2013):Experimental bit commitment based on quantum communication and special relativity.https://arxiv.org/pdf/1306.4801.pdf.

Luo,Q.B.;Yang,G.W.;She,K.;Li,X.Y.;Fang,J.B.(2016):Quantum homomorphic signature based on bell-state measurement.Quantum Information Processing,vol.15,no,12,pp.5051-5061.

Ma,H.X.;Huang,P.;Bao,W.S.;Zeng,G.H.(2016):Continuous-variable quantum identity authentication based on quantum teleportation.Quantum Information Processing,vol.15,no.6,pp.2605-2620.

Ma,L.J.;Mink,A.;Tang,X.(2009):High speed quantum key distribution over optical fiber network system.Journal of Research of the National Institute of Standards and Technology,vol.114,no.3,pp.149-177.

Ma,X.S.;Herbst,T.;Scheidl,T.;Wang,D.;Kropatschek,S.et al.(2012):Quantum teleportation over 143 kilometres using active feed-forward.Nature,vol.489,no.7415,pp.269-273.

Masanes,L.;Renner,R.;Christandl,M.;Winter,A.;Barrett,J.(2014):Full security of quantum key distribution from no-signaling constraints.IEEE Transactions on Information Theory,vol.60,no.8,pp.4973-4986.

Mayers,D.(1996):The trouble with quantum bit commitment.https://arxiv.org/pdf/quant-ph/9603015.pdf.

Mayers,D.(1997):Unconditionally secure quantum bit commitment is impossible.Physical Review Letters,vol.78,no.17,pp.3414-3417.

William,S.;Razieh,A.;Ma,X.F.;Lütkenhaus,N.(2015):Security of quantum key distribution using a simplified trusted relay.https://arxiv.org/pdf/1408.4426.pdf.

Mirza,A.;Petruccione,F.(2010):Realizing long-term quantum cryptography.Journal of the Optical Society of America B,vol.27,no.6,pp.185-188.

Mochon,C.(2005):A large family of quantum weak coin-flipping protocols.https://arxiv.org/pdf/quant-ph/0502068.pdf.

Nagy,M.;Nagy,N.(2017):Quantum oblivious transfer:a secure practical implementation.Quantum Information Processing,vol.15,no.12,pp.5037-5050.

Naor,M.;Ostrovsky,R.;Venkatesan,R.;Yung,M.(1998):Perfect zero-knowledge arguments for NP using any one-way permutation.Journal of Cryptology,vol.11,no.2,pp.87-108.

Naseri,M.;Raji,M.A.;Hantehzadeh,M.R.;Vicente,M.(2015):A scheme for secure quantum communication network with authentication using GHZ-like states and cluster states controlled teleportation.Quantum Information Processing,vol.14,no.11,pp.4279-4295.

Nielsen,M.A.;Knill,E.;Laflamme,R.(1998):Complete quantum teleportation using nuclear magnetic resonance.Nature,vol.396,no.6706,pp.52-55.

Noh,T.G.(2009):Counterfactual quantum cryptography.https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.103.230501.

Pattaranantakul,M.;Janthong,A.;Sanguannam,K.;Sanguannam,P.;Pattaranantakul,M.et al.(2015):Efficient key management protocol for secure RTMP video streaming toward trusted quantum network.ETRI Journal,vol.37,no.4,pp.696-706.

Peng,C.Z.;Yang,T.;Bao,X.H.;Zeng,J.;Jin,X.M.et al.(2005):Experimental free-space distribution of entangled photon pairs over 13 km:towards satellite-based global quantum communication.https://arxiv.org/pdf/quant-ph/0412218.pdf.

Pereira,J.;Pirandola,S.(2018):Hacking alice's box in continuous-variable quantum key distribution.https://journals.aps.org/pra/abstract/10.1103/PhysRevA.98.062319.

Peter,S.;Stefan,R.(2009):How to overcome the “trusted node model” in quantum cryptography.Procceding of the 12th IEEE International Conference on Computational Science and Engineering,pp.259-262.

Pfaff,W.;Hensen,B.J.;Bernien,H.;van Dam,S.B.;Blok,M.S.et al.(2014):Unconditional quantum teleportation between distant solid-state quantum bits.Science,vol.345,no.6196,pp.532-535.

Pirandola,S.;Eisert,J.;Weedbrook,C.;Furusawa,A.;Braunstein,S.L.(2015):Advances in quantum teleportation.Nature Photonics,vol.9,no.10,pp.641-652.

Poppe,A.;Peev,M.;Maurhart,O.(2008):Outline of the secoqc quantum key distribution network in vienna.International Journal of Quantum Information,vol.6,no.2,pp.209-218.

Qin,H.W.;Tang,W.S.;Tso,R.(2018):Multiparty to multiparty quantum secret sharing.https://www.worldscientific.com/doi/abs/10.1142/S0217984918503505.

Qin,H.W.;Tang,W.S.;Tso,R.(2018):Batch quantum multi-proxy signature.https://link.springer.com/content/pdf/10.1007%2Fs11082-018-1707-6.pdf.

Ren,H.F.;Wang,Q.L.;Lian,R.M.;Hou,S.X.(2014):A scheme to cancel out superiority of quantum strategies in coin-tossing game.Indian Journal of Physics,vol.88,no.3,pp.271-274.

Richard,J.H.;Jane,E.N.;Kevin,P.M.;McCabe,K.P.;Newell,R.T.et al.(2013):Network-centric quantum communications with application to critical infrastructure protection.https://arxiv.org/ftp/arxiv/papers/1305/1305.0305.pdf.

Roa,L.;Dolgado,A.;Fuentes-Guridi,I.(2003):Optimal conclusive teleportation of quantum states.https://arxiv.org/pdf/quant-ph/0304002.pdf.

Roberts,G.L.;Lucamarini,M.;Dynes,J.F.;Savory,S.J.;Yuan,Z.L.(2017):Manipulating photon coherence to enhance the security of distributed phase reference quantum key distribution.https://aip.scitation.org/doi/10.1063/1.5004488.

Salvail,L.(1998):Quantum bit commitment from a physical assumption.Advances in Cryptology Proceedings of Crypto'98,pp.338-354.

Salvail,L.;Peev,M.;Diamanti,E.;Alléaume,R.;Lütkenhaus,N.et al.(2010):Security of trusted repeater quantum key distribution networks.Journal of Computer Security,vol.18,no.1,pp.61-87.

Sasaki,M.;Fujiwara,M.;Ishizuka,H.;Klaus,W.;Wakui,K.et al.(2011):Field test of quantum key distribution in the Tokyo QKD network.Optics Express,vol.19,no.11,pp.10387-10409.

Schaffner,C.(2010):Simple protocols for oblivious transfer and secure identification in the noisy-quantum-storage model.https://arxiv.org/pdf/1002.1495.pdf.

Sharma,V.(2012):Enterprise security services using continuous variable QKD.Report PPT at First NASA Quantum Future Technologies Conference,pp.126-137.

Shi,R.H.;Mu,Y.;Zhong,H.;Cui,J.;Zhang,S.(2016):Secure multiparty quantum computation for summation and multiplication.https://www.nature.com/articles/srep19655.pdf.

Shor,P.W.(1994):Algorithms for quantum computation:discrete logarithms and factoring.Proceedings of the 35th Annual IEEE Symposium on Foundations of Computer Science,pp.124-134.

Sikora,J.(2012):On the existence of loss-tolerant quantum oblivious transfer protocols.Quantum Information ＆ Computation,vol.12,no.7-8,pp.609-619.

Song,Y.Q.;Yang,L.(2018):Practical quantum bit commitment protocol based on quantum oblivious transfer.https://www.mdpi.com/2076-3417/8/10/1990/htm.

Sripimanwat,K.(2012):Secure and efficient key management technique in quantum cryptography network.Proceedings of the 4th International Conference on Ubiquitous and Future Networks,pp.280-285.

Stucki,D.;Gisin,N.;Guinnard,O.;Ribordy,G.;Zbinden,H.(2002):Quantum key distribution over 67 km with a plug ＆ play system.New Journal of Physics,vol.4,no.41,pp.1-8.

Stucki,D.;Legré,M.;Buntschu,F.;Clausen,B.;Felber,N.et al.(2011):Long-term performance of the swiss quantum quantum key distribution network in a field environment.http://iopscience.iop.org/article/10.1088/1367-2630/13/12/123001/pdf.

Sun,M.Z.;Peng,X.;Shen,Y.;Guo,H.(2012):Security of a new two-way continuousvariable quantum key distribution protocol.https://arxiv.org/pdf/1110.1818.pdf.

Sun,Y.;Xu,S.W.;Chen,X.B.;Niu,X.X.;Yang,Y.X.(2013):Expansible quantum secret sharing network.Quantum Information Processing,vol.12,no.8,pp.2877-2888.Sun,Y.M.;Cheng,X.Z.;Ji,Y.F.(2014):A differentialized service providing scheme on trusted relay quantum key distribution networks.http://www.photon.ac.cn/EN/abstract/abstract20522.shtml.

Tang,X.;Ma,L.J.;Mink,A.;Chang,T.J.;Xu,H.et al.(2008):High-speed quantum key distribution system for optical fiber networks in campus and metro areas.Quantum Communications and Quantum Imaging VI,vol.7092,no.709201,pp.1-15.

Tang,Y.L.;Yin,H.L.;Chen,S.J.;Liu,Y.;Zhang,W.J.et al.(2014):Measurement-device-independent quantum key distribution over 200 km.https://arxiv.org/pdf/1407.8012.pdf.

Tittel,W.;Zbinden,H.;Gisin,N.(2001):Experimental demonstration of quantum secret sharing.https://journals.aps.org/pra/abstract/10.1103/PhysRevA.63.042301.

Ursin,R.;Jennewein,T.;Kofler,J.;Perdigues,J.M.;Cacciapuoti,L.et al.(2009):Space-quest:experiments with quantum entanglement in space.Europhysics News,vol.40,no.3,pp.26-29.

Wang,C.;Deng,F.G.;Li,Y.S.;Liu,X.S.;Long,G.L.(2005):Quantum secure direct communication with high-dimension quantum superdense coding.https://journals.aps.org/pra/abstract/10.1103/PhysRevA.71.044305.

Wang,J.(2007):Theoretical Study of Quantum Cryptographic Protocols (Ph.D.Thesis).National University of Defense Technology,China (in Chinese).

Wang,J.;Zhang,Q.;Tang,C.J.(2006):Quantum signature scheme with message recovery.Proceedings of the 8th International Conference on Advanced Communication Technology,pp.1375-1378.

Wang,J.;Zhang,Q.;Tang,C.J.(2008):Efficient quantum signature protocol of classical messages.Journal of Communications,vol.28,no.1,pp.64-68 (In Chinese).

Wang,L.;Zou,L.;Zhao,S.M.(2014):A novel quantum secret sharing scheme with a trustful center.Chinese Journal of Quantum Electronics,vol.31,no.5,pp.591-598.

Wang,M.L.;Ma,W.P.;Wang,L.L.;Yin,X.R.(2015):A quantum proxy group signature scheme based on an entangled five-qubit state.https://www.worldscientific.com/doi/abs/10.1142/S0217984915501730.

Wang,S.;Chen,W.;Yin,Z.Q.;Zhang,Y.;Zhang,T.et al.(2010):Field test of wavelength-saving quantum key distribution network.Optics Letters,vol.35,no.14,pp.2454-2456.

Wang,T.Y.;Wen,Q.Y.;Zhu,F.C.(2010):Quantum communications with an anonymous receiver.Science in China Series G:Physics,Mechanics ＆ Astronomy,vol.53,no.12,pp.2227-2231.

Wang,Y.W.;Zhan,Y.B.(2009):A theoretical scheme for zero-knowledge proof quantum identity authentication.Acta Physica Sinica,vol.58,no.11,pp.7668-7671.

Wei,H.J.;Liu,Y.H.;Sun,X.;Song,L.J.(2018):Identity-based encryption scheme based on cloud and quantum keys.Journal of Jilin University (Engineering and Technolgy Edition),vol.48,no.2,pp.551-557.

Wen,X.J.;Chen,Y.Z.;Fang,J.B.(2013):An-inter-bank e-payment protocol based on quantum proxy blind signature.Quantum Information Processing,vol.12,no.1,pp.549-588.

Wen,X.J.;Tian,Y.;Ji,L.P.;Niu,X.M.(2010):A group signature scheme based on quantum teleporation.http://iopscience.iop.org/article/10.1088/0031-8949/81/05/055001.

Wengerowsky,S.;Joshi,S.K.;Steinlechner,F.;Hübel,H.;Ursin,R.(2018):An entanglement-based wavelength-multiplexed quantum communication network.Nature,vol.564,no.7735,pp.225-228.

Wu,D.;Yu,W.R.;Zhao,B.K.;Wu,C.Q.(2014):Quantum key distribution in large scale quantum network assisted by classical routing information.International Journal of Theoretical Physics,vol.53,no.10,pp.3503-3511.

Wu,H.;Wang,X.B.;Pan J.W.(2014):Quantum communication:status and prospects.Science China:Information Sciences,vol.44,no.3,pp.296-311 (In Chinese).

Wu,Y.H.;Zhai,W.D.;Cao,W.Z.;Li,C.(2011):Quantum secure direct communication by using general entangled states.International Journal of Theoretical Physics,vol.50,no.2,pp.325-331.

Xiao,L.;Long,G.L.;Deng,F.G.;Pan,J.W.(2004):Efficient multiparty quantumsecret-sharing schemes.https://arxiv.org/pdf/quant-ph/0405179v1.pdf.

Xu,B.J.;Liu W.L.;Mao,J.Q.;Yang Y.(2014):Research on development status and existing problems of quantum communication technology.Communications Technology,vol.47,no.5,pp.463-468 (In Chinese).

Xu,R.;Huang,L.S.;Yang,W.;He,L.B.(2011):Quantum group blind signature scheme without entanglement.Optics Communications,vol.284,no.14,pp.3654-3658.

Yang,L.;Ma,H.Y.;Zheng,C.;Ding,X.L.;Gao,J.C et al.(2017):Quantum communication scheme based on quantum teleportation.http://wulixb.iphy.ac.cn/CN/10.7498/aps.66.230303.

Yang,W.;Huang,L.S.;Yao,Y.F.;Chen Z.L.(2007):Quantum oblivious transfer using tripartite entangled state.Proceedings of 2007 International Conference on Future Generation Communication and Networking,pp.189-196.

Yang,Y.G.(2008):Multi-proxy quantum group signature scheme with threshold shared verification.Chinese Physics B,vol.17,no.2,pp.415-418.

Yang,Y.G.;Wang,H.Y.;Jia,X.;Zhang,H.(2013):A quantum protocol for (t,n)-threshold identity authentication based on greenberger-horne-zeilinger States.International Journal of Theoretical Physics,vol.52,no.2,pp.524-530.

Yang,Y.G.;Wen,Q.Y.(2008):Threshold quantum secret sharing between multi-party and multi-party.Science in China Series G:Physics,Mechanics ＆ Astronomy,vol.51,no.9,pp.1308-1315.

Yang,Y.G.;Wen,Q.Y.(2008):Multiparty simultaneous quantum identity authentication with secret sharing.Science in China Series G:Physics,Mechanics ＆ Astronomy,vol.51,no.3,pp.321-327.

Yang,Y.G.;Wen,Q.Y.(2009):Economical multiparty simultaneous quantum identity authentication based on greenberger-horne-zeilinger states.Chinese Physics B,vol.18,no.8,pp.3233-3237.

Yang,Y.G.;Yang,R.;Lei,H.;Shi,W.M.;Zhou,Y.H.(2015):Quantum oblivious transfer with relaxed constraints on the receiver.Quantum Information Processing,vol.14,no.8,pp.3031-3040.

Yao,A.C.(1982):Protocol for secure computations.Proceedings of the 23rd Annual Symposium on Foundations of Computer Science,pp.160-163.

Yin,J.;Ren,J.G.;Lu,H.;Cao,Y.;Yong,H.L.et al.(2012):Quantum teleportation and entanglement distribution over 100-kilometre free-space channels.Nature,vol.488,no.7410,pp.185-188.

Yin,X.R.;Ma,W.P.;Liu,W.Y.(2012):A blind quantum signature scheme with χtype entangled states.International Journal of Theoretical Physics,vol.51,no.2,pp.455-461.

You,X.M.;Liu,S.;Wang,Y.M.(2012):Quantum-behaved network rsource parallel allocation optimization model and application.Journal of Jilin University (Engineering and Technology Edition),vol.42,no.S1,pp.341-345 (In Chinese).

Yu,C.H.;Guo,G.D.;Lin,S.(2014):Arbitrated quantum signature scheme based on reusable key.Science in China Series G:Physics,Mechanics ＆ Astronomy,vol.57,no.11,pp.2079-2085.

Yuan,H.;Liu,Y.M.;Pan,G.Z.;Zhang,G.;Zhou,J.et al.(2014):Quantum identity authentication based on ping-pong technique without entanglements.Quantum Information Processing,vol.13,no.11,pp.2535-2549.

Yuan,H.;Zhang,Q.;Hong,L.;Yin,W.J.;Xu,D.et al.(2014):Scheme for deterministic secure quantum communication with three-qubit GHZ state.International Journal of Theoretical Physics,vol.53,no.8,pp.2558-2564.

Zawadzki,Piotr.(2019):Quantum identity authentication without entanglement.https://link.springer.com/content/pdf/10.1007%2Fs11128-018-2124-2.pdf.

Zhandry,M.(2012):Secure identity-based encryption in the quantum random oracle model.https://link.springer.com/content/pdf/10.1007%2F978-3-642-32009-5_44.pdf.

Zhang,S.B.;Xie,Z.H.;Yin Y.F.;Chang,Y.;Sheng,Z.W.et al.(2017):Study on quantum trust model based on node trust evaluation.Chinese Journal of Electronics,vol.26,no.3,pp.608-613.

Zhang,Z.J.;Li,Y.;Man,Z.X.(2005):Multiparty quantum secret sharing.https://arxiv.org/pdf/quant-ph/0412203v1.pdf.

Zhang,Z.R.;Liu,W.T.;Li,C.Z.(2011):Quantum secret sharing based on quantum error-correcting codes.https://www.onacademic.com/detail/journal_1000037732851910_cdc3.html.

Zhang,Z.S.;Zeng,G.H.;Zhou,N.R.;Xiong,J.(2006):Quantum identify authentication based on ping-pong technique for photons.Physics Letters A,vol.356,no.3,pp.199-205.

Zhao,L.Y.;Yin,Z.Q.;Wang,S.;Chen,W.;Chen,H.et al.(2015):Measurementdevice-independent quantum coin tossing.https://arxiv.org/pdf/1512.09269.pdf.

Zeng,G.H.(2008):Reply to “comment on ‘arbitrated quantum-signature scheme'”.https://journals.aps.org/pra/abstract/10.1103/PhysRevA.78.016301.

Zeng,G.H.;Keitel,C.H.(2002):An arbitrated quantum-signature scheme.https://arxiv.org/pdf/quant-ph/0109007v2.pdf.

Zeng,G.H.;Ma,W.P.;Wang,X.M.;Zhu,H.W.(2001):Signature scheme based on quantum cryptography.Acta Electronica Sinica,vol.29,no.8,pp.1098-1100.

Zeng,G.H.;Zhang,W.P.(2001):Identity verification in quantum key distribution.Physical Review A,vol.2003,no.61,pp.22-23.

Zheng,S.B.;Guo,G.C.(1997):Teleportation of an unknown atomic state through the Raman atom-cavity-field interaction.Physics Letters A,vol.232,vol.1,pp.171-174.

Zheng,Y.Z.;Gu,Y.J.;Guo,G.C.(2002):Teleportation of a three-particle entangled W state.Chinese Physics B,vol.11,no.6,pp.537-542.

Zhou,C.Y.;Wu,G.;Chen,X.L.;Li,H.X.;Zeng,H.P.(2003):Quantum secure communication in 50 km optical fiber.Science in China Series G:Physics,Mechanics ＆ Astronomy,vol.33,no.6,pp.538-543.

Zhou,J.;Lu,L.F.;Lei,Y.Q.;Chen,X.(2014):Research on improving security of protection for power system secondary system by quantum key technology.Smart Grid Technology,vol.38,no.6,pp.1518-1522 (In Chinese).

Zhou,L.(2012):Quantum Entanglement Percolation in Complex Networks (Ph.D.Thesis).Soochow University,China (In Chinese).

Zhou,N.R.;Zeng,G.H.;Zeng,W.J.;Zhu,F.C.(2005):Cross-center quantum identification scheme based on teleportation and entanglement swapping.Optics Communications,vol.254,no.4-6,pp.380-388.