机收麻山药离散元模型构建及其仿真参数标定
2019-12-19郝建军龙思放贾雅丽马志凯赵建国
郝建军,龙思放,李 浩,贾雅丽,马志凯,赵建国
机收麻山药离散元模型构建及其仿真参数标定
郝建军1,龙思放1,李 浩1,贾雅丽2,马志凯1,赵建国1
(1. 河北农业大学机电工程学院,保定 071001;2. 河北省农业机械鉴定监理总站,石家庄 050031)
由于麻山药收获过程缺乏有效数值模拟,在很大程度上阻碍了麻山药收获机的设计与优化。该文测定了麻山药的密度、长度、径向尺寸、抗压、抗弯及抗剪强度,基于离散元法建立了麻山药双峰分布模型,并对黏结参数进行校核;以土壤堆积角为响应值,对沙壤土基质间的碰撞恢复系数、静摩擦因数、滚动摩擦因数和表面能4个参数进行标定,建立了土壤堆积角与4个参数之间的回归模型并进行验证,标定了麻山药与钢板、沙壤土间的碰撞恢复系数、静摩擦因数和滚动摩擦因数。试验结果表明,麻山药双峰分布模型能够表征麻山药的力学特性,参数校核得到法向刚度、切向刚度、临界法向应力、临界切向应力及黏结半径分别为9.3×105N/m、3.0×106N/m、0.58 MPa、0.14 MPa、3.5 mm;沙壤土基质间的碰撞恢复系数、静摩擦因数、滚动摩擦因数及表面能分别为0.42、0.20、0.30、0.40 J/m3,离散元仿真试验后得到的土壤堆积角与试验结果平均误差为1.48%;麻山药与钢板之间的碰撞恢复系数、静摩擦因数及滚动摩擦因数分别为0.34、0.26、0.049,与沙壤土之间的碰撞恢复系数、静摩擦因数及滚动摩擦因数分别为0.21、0.38、0.075。研究结果可为麻山药机械化收获及产后加工等仿真试验提供一定的理论参考。
农作物;模型;离散元法;麻山药;参数标定
0 引 言
麻山药是药食同源的名贵食材,在中国具有悠久的栽培历史。其主产于河南、河北、山东、江苏、湖北、安徽、山西等地。随着生活水平的提高,富含多种维生素、氨基酸,且兼具食药两用的麻山药及其加工制品备受青睐。麻山药扎根较深,在地表以下0.6~1.2 m不等,收获过程中极易划伤或折断。在中国,小面积麻山药种植区多以人工挖掘收获为主;较大面积种植区多采用挖沟机先在麻山药两行间开出一条深沟,然后人工再用铁锹挖掘。收获过程机械化程度低、费时费力,而且极易对麻山药造成损伤,影响品质。
目前针对麻山药收获的研究主要集中在物理试验方面,较少涉及数值模拟研究工作,所以有必要利用便捷的研究方法实现麻山药收获过程可视化、参数化。EDEM是国际通用的基于离散单元法模拟和分析颗粒系统的CAE软件,目前已在农业领域得到了广泛应用[1-6]。其中Hertz-Mindlin with bonding黏结模型能够模拟农作物在收获、加工过程中的破碎现象,广泛应用于农业物料建模领域[7-8]。国内外学者进行参数标定及校核[9-11],大多是根据理论公式计算出BPM模型所需黏结参数值,再通过物理试验去验证选定的参数值,使虚拟试验表观结果与物理试验结果相近似,选择表观特征变化最接近的一组参数作为农作物破碎仿真中使用的黏结参数。这类方法能够定性分析物料破碎状态,对于物料破碎时所受外力的定量分析相对不够精确。本文基于Hertz-Mindlin with bonding黏结模型建立小白嘴麻山药双峰分布模型,并对适宜其种植的沙壤土的物理特性及两者间的接触参数进行标定,利用物理试验与虚拟试验相结合的方法校核麻山药离散元模型以及所标定参数的准确性。研究结果可为分析麻山药在收获过程中的运动、受力状态及破损方式提供理论基础。
1 麻山药离散元模型建立及参数校核
1.1 麻山药力学特性参数测定
为保证麻山药在收获过程中不受损伤,需分析其在收获过程中的受力状态并建立其离散元模型。为此,要得到麻山药的三轴尺寸和力学参数。本文以河北省安平县普遍种植的小白嘴麻山药为研究对象,其物理特性参数为:长度400~900 mm,径向尺寸为20~45 mm,平均密度为1 010 kg/m3,平均含水率为80%。采用HY-0580微型机电子万能力学试验机,通过压缩、弯曲、剪切试验测量其力学特性参数。
麻山药的弹性模量是求得剪切模量的先决条件。材料在弹性变形阶段时,其应力和应变成正比关系,比例系数则为弹性模量。弹性形变符合胡克定律,压缩与弯曲弹性模量计算公式分别为
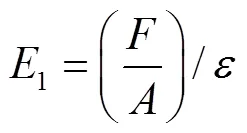
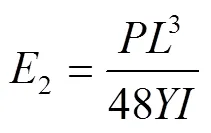
式中1为压缩弹性模量,MPa;为载荷,N;为截面面积,mm2;为应变;2为弯曲弹性模量,MPa;为载荷,N;为跨距,mm;为弯曲挠度,mm;为截面惯性矩,mm4。经试验与计算得到麻山药力学参数,如表1所示。由表中数据可知,麻山药轴向与径向弹性模量较为接近,结构较均质。
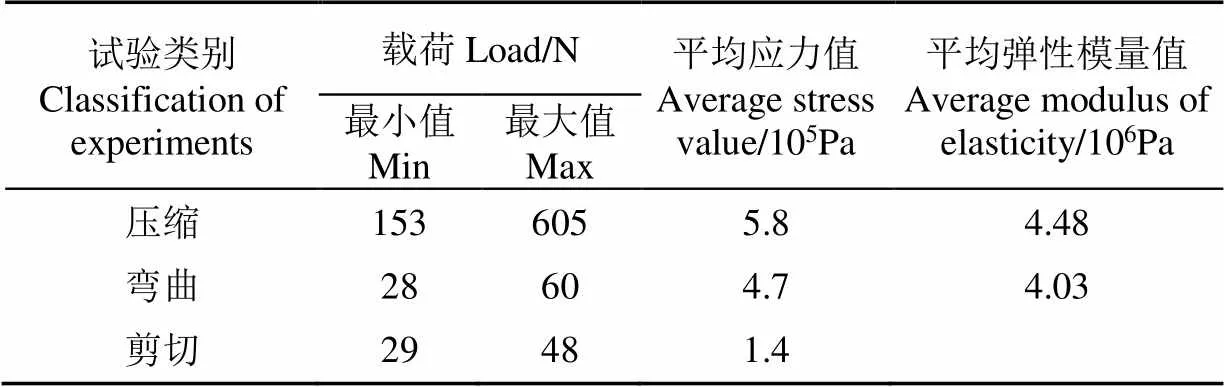
表1 麻山药力学试验结果
1.2 麻山药根茎结构模型构建
组成颗粒群的球形颗粒粒径分布方式包括单一分布、高斯分布和双峰分布,不同的颗粒粒径分布方式会导致颗粒间黏结键分布密度、长短、数量的不同,如图1所示。其中单一分布采用球形颗粒等粒径排布而成,颗粒周围黏结键分布均匀,对破碎对象的力学特性不能很好的描述;高斯分布中具有非等粒径球形颗粒,颗粒间黏结键疏密分布,较单一分布能够更好的反映破碎对象的力学特性。而组成双峰分布的颗粒粒径服从正态分布,大颗粒占据主要空间位置,小颗粒则紧密排布在大颗粒周围,颗粒具有较高的配位数,从而提高了颗粒群的填充密度,降低了孔隙率,保证了模型具有很好的黏结强度[12]。
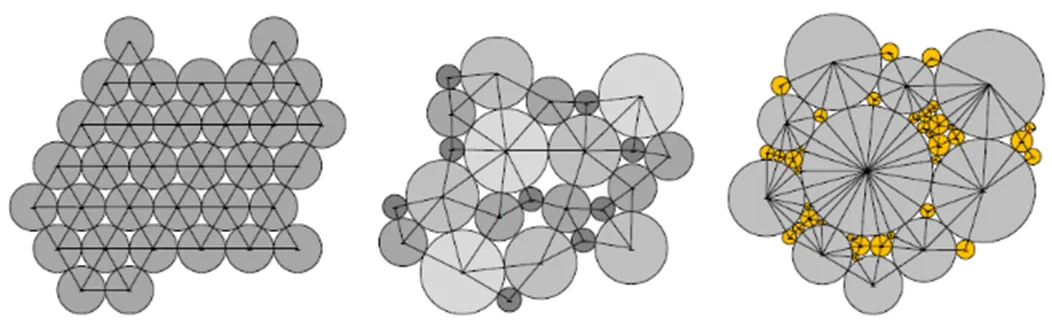
a. 单一分布a. Mono distributionb. 高斯分布b. Gaussian distributionc. 双峰分布c. Bimodal distribution
本文使用双峰分布堆积方式对麻山药建模(大尺度颗粒:平均半径3 mm,标准差0.2 mm;小尺度颗粒:平均半径1 mm,标准差0.2 mm),共9 887个非等粒径的颗粒、111 723个有效黏结键,平均单个球体配位数约为11,孔隙率较低,能更好的模拟麻山药力学特征,如图2a所示。参考相关学者对研究对象的处理方法[6,13-15]及力学试验结果,将麻山药等效为各向同性结构,泊松比取值0.4[2]。另外,麻山药根茎表面有直径小于1 mm、长度0~50 mm不等且与麻山药主根茎连接、容易断裂的毛细根,收获过程中所表现出与土壤之间的黏结力可以忽略不计,在模型中可将其略去。图2b为添加BPM黏结键后的麻山药离散元模型正、俯视截面图。
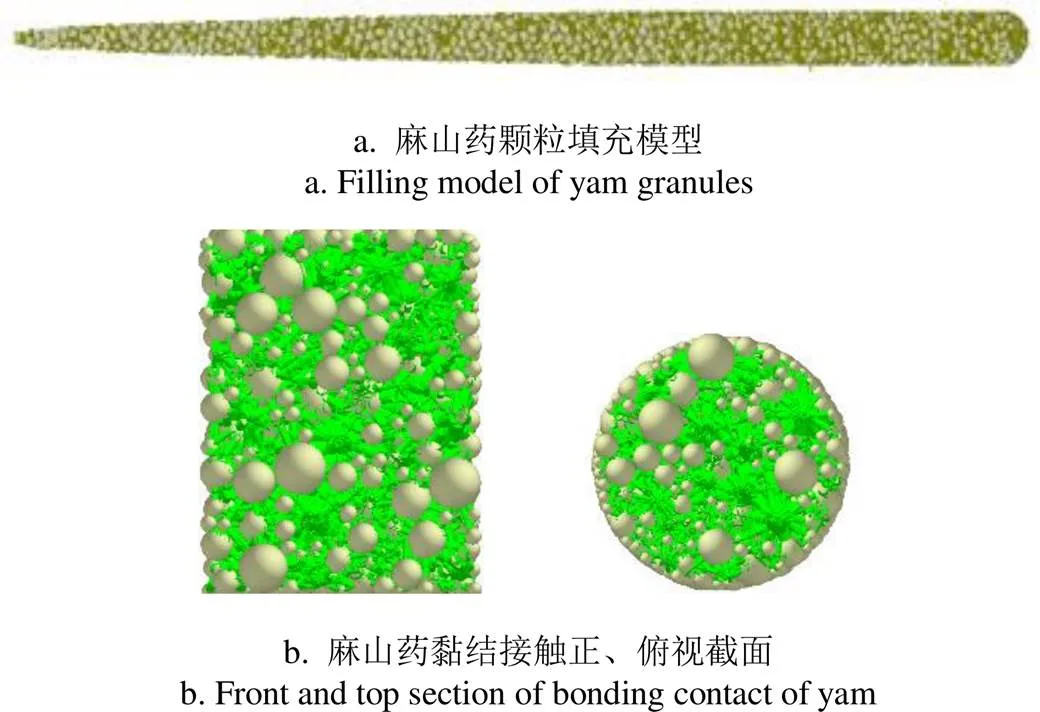
图2 麻山药离散元模型
1.3 黏结参数确定及校验
本文根据麻山药力学试验结果,参考国内外相关学者研究理论基础对麻山药黏结参数进行标定,在离散元软件中进行压缩和剪切仿真试验,选择曲线特征变化与实际力学试验结果最为接近的一组参数,使标定结果更加精确。
1.3.1 BPM黏结参数确定
结合麻山药力学特性曲线图,法向刚度K用式(3)计算[7]
K=DF/D(3)
式中DF为垂直于麻山药的载荷增量,N;D为麻山药产生的形变增量,mm。
前文对麻山药进行力学试验后得到麻山药形变与载荷关系曲线,如图3a所示。

图3 麻山药形变与载荷关系图
段为弹性形变阶段,随着负载的增加,麻山药形变呈线性增加。截取段进行分析,线性关系如图3b所示。对形变和负载进行一元线性回归分析,回归方程中=99.642,决定系数2为0.995 6。根据公式(3)可以得到法向刚度为斜率的103。选取5个样品进行测量,取的平均值,即得法向刚度K=100 201 N/m。
切向刚度K为法向刚度K的2/3~1,研究中取切向刚度为法向刚度的1倍[16],故得到法向刚度系数与切向刚度系数均为100 201 N/m。由前文轴向压缩试验可得,平均压缩临界载荷为400 N,由抗压强度公式:/,其中为压力,为受力面积,为临界法向应力。得:=0.58 MPa。根据弹性结构体切应力计算公式,得到麻山药破碎中临界切向应力为:=0.14 MPa。颗粒黏结半径一般为颗粒半径的1.1~1.2倍,本文中取黏结半径为3.5 mm。
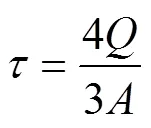
式中是临界切向应力,Pa;是剪切载荷,N;是受剪截面面积,mm2。
1.3.2 参数修正试验与结果
在进行虚拟预试验过程中,虚拟试样所承受最大压缩和剪切载荷与实际值比较存在误差。因此参考上文理论计算值数量级和国内学者研究方法[17],在EDEM软件中进行虚拟压缩与剪切修正试验,以最大压缩载荷及最大剪切力作为响应值(分别用1、2表示),对这2个黏结参数进行进一步修正,结果表明随着2个参数数值的增加,麻山药模型抗压与抗剪载荷均呈现上升趋势,且切向刚度值对于麻山药模型的抗破坏能力影响大于法向刚度值。试验因素编码值与仿真试验结果如表2所示。使用State-East公司的Design-Expert V8.0.6.1软件对试验数据进行响应面分析,结果如表3、4所示,得到优化后的回归模型分别为

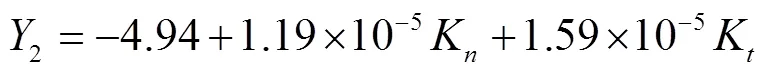
应用Design Expert 8.0.6.1软件对2个回归模型以最初设计点为起始点求解,使模拟结果尽可能满足麻山药压缩和剪切力学试验所得到的力学曲线特征,最终得到一组最优标定结果如表5所示。
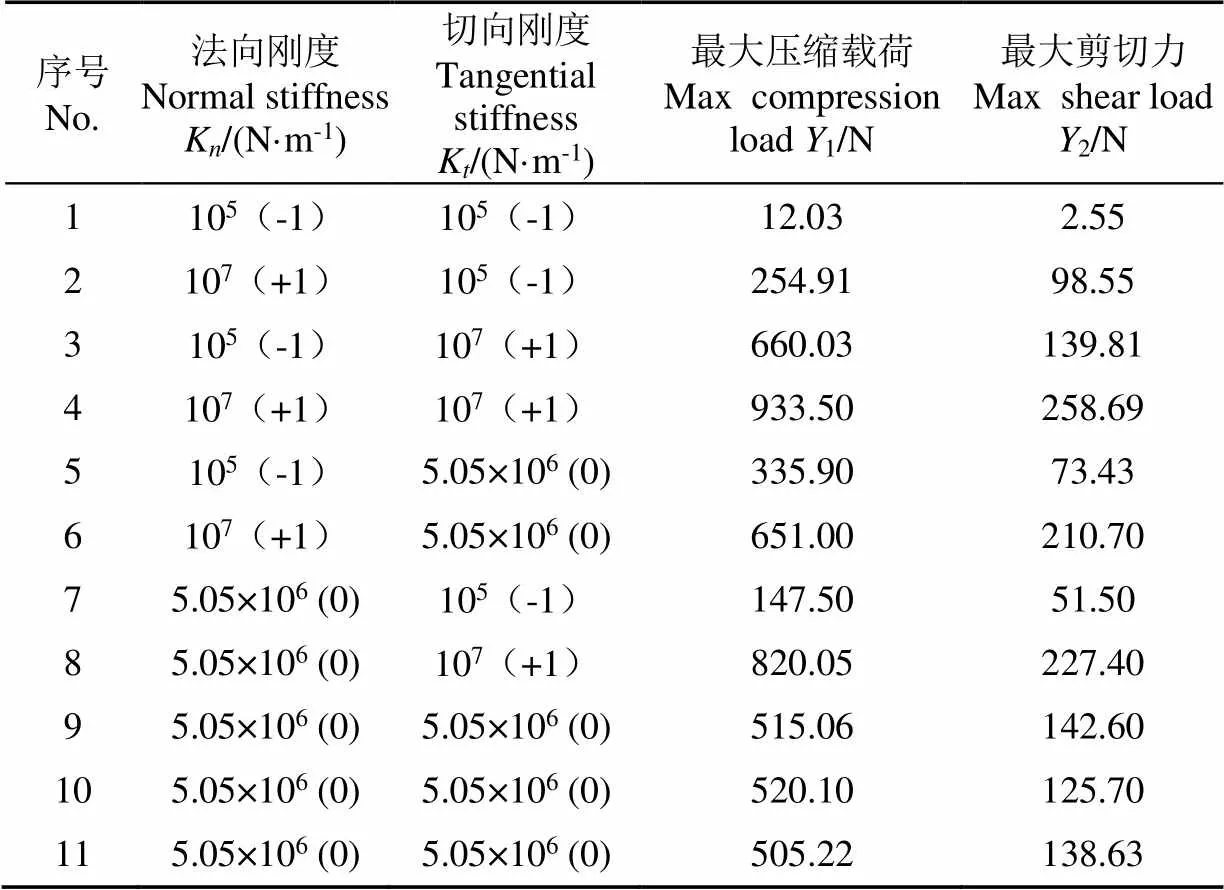
表2 仿真试验方案与结果

表3 Y1模型方差分析
注:**极显著(<0.01)*显著(<0.05),下同。
Note: ** is highly significant (<0.01), * is significant (<0.05), the same below.

表4 Y2模型方差分析

表5 BPM黏结参数
1.3.3 BPM黏结参数校验
利用虚拟标定所得的黏结参数在EDEM软件中对长40 mm的仿真试样进行压缩和剪切试验,将压缩载荷-形变曲线特征及剪切力-位移曲线特征与实际力学试验结果进行比对,校核黏结参数。
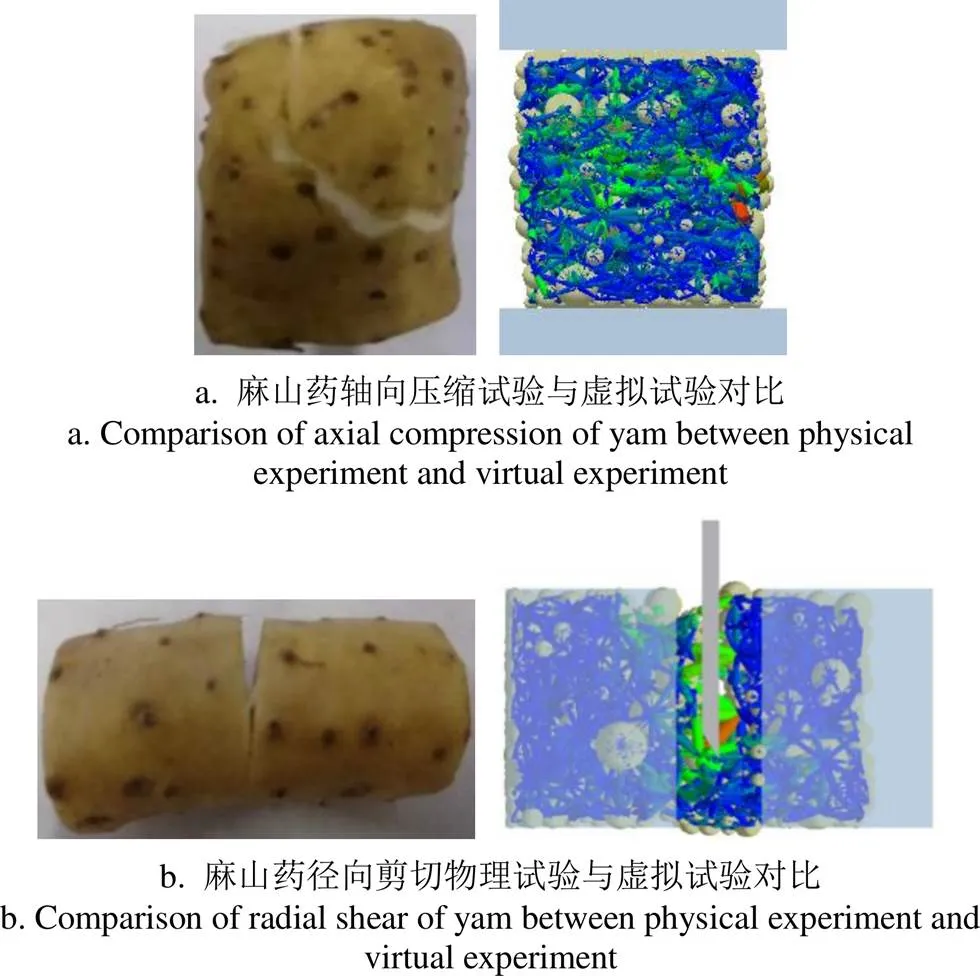
图4 麻山药模型仿真试验
从图4a看出,麻山药经过轴向压缩后,最大应力集中在表皮中部,断裂趋势自左向右倾斜延伸。在虚拟试验中由应力云图也可以看到最大应力集中于虚拟试样表皮中部。两者破裂形式基本一致。从图4b看出,麻山药径向剪切破坏后,由外表皮至内部纤维被切断。虚拟试验中对试样进行径向剪切时,颗粒间黏结键断裂,最大应力集中于刀刃处。两者切口宽度与刀片厚度相一致,且试样在虚拟试验中的剪切破坏行为与物理试验基本吻合。由图5可以看出,仿真试样的压缩载荷-形变曲线与相邻曲线特征基本一致,较平均峰值水平偏低,剪切力-位移曲线峰值稍高于平均水平,原因是法向刚度K与切向刚度K不断变化的过程中,剪切力随之变化的灵敏程度较压缩载荷高,但两曲线整体的特征趋势与力学试验结果基本相符。综上所述,经过以上步骤所得的麻山药最优黏结参数所表现出来的力学特征值与麻山药实际情况较为接近,能够表征麻山药的基本力学特性。

图5 麻山药压缩、剪切试验载荷-位移曲线
2 沙壤土参数标定
2.1 试验材料与方法
采用土壤堆积角试验法对沙壤土基质间的接触参数进行标定,仿真模型如图6所示。由于麻山药种植于沙壤土中,颗粒之间存在一定的黏附关系,选用Hertz-Mindlin with JKR接触模型[18]作为土壤基质间的接触模型。试验中所用土壤取自河北省安平县麻山药种植田,土质松散、无结块现象、粒径大部分在4 mm以下,属于沙质土壤。称量计算可知土样平均容重1 362 kg/m3。在烘干箱中烘干土样直至质量恒定,称量计算得到平均含水率为14.15%,仿真参数见表6[5-6,19-20]。土壤堆积试验中所用漏斗进料口径为100 mm,出料口径为16 mm,出料口与堆积底板间的高度差为110 mm。试验时,漏斗中的土壤颗粒经漏斗出料口落于堆积底座上,在侧面对堆积体进行拍照,使用MATLAB将获取的图像进行灰度化、二值化处理,并使用Canny算子进行边缘检测,再将图像导入Origin软件获取轮廓点坐标,得到散点图之后,用高斯分布对其进行拟合,找到图像拐点。然后取拐点切线与轴所夹锐角为土壤的堆积角[21],试验过程如图7a、b、c所示。
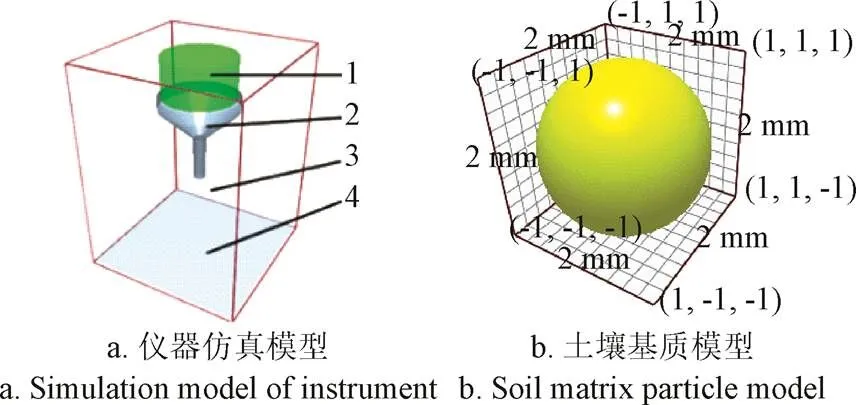
1.颗粒工厂 2.漏斗 3.计算域 4.堆积底板
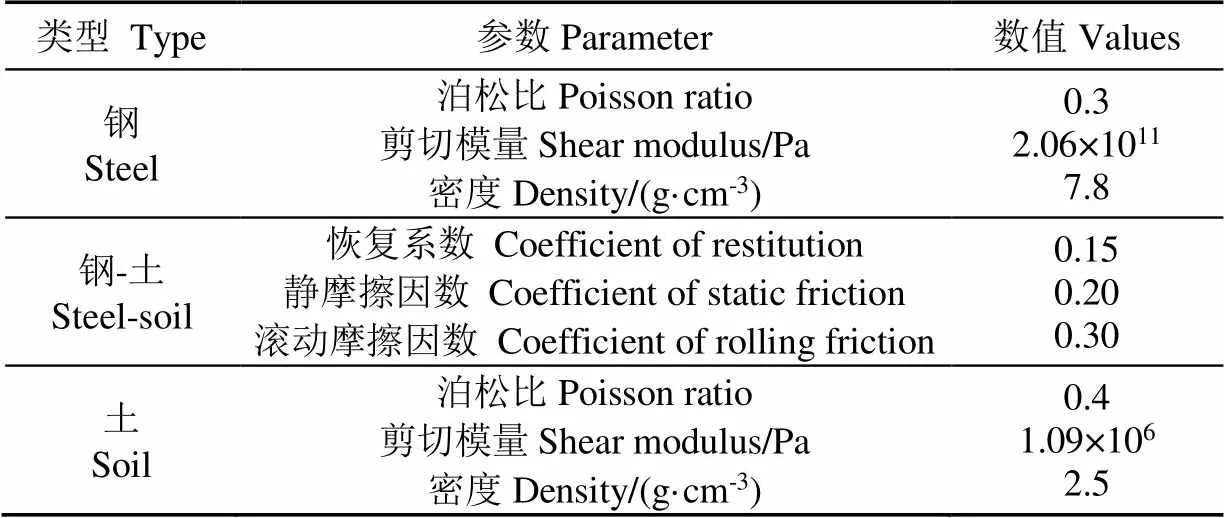
表6 仿真参数
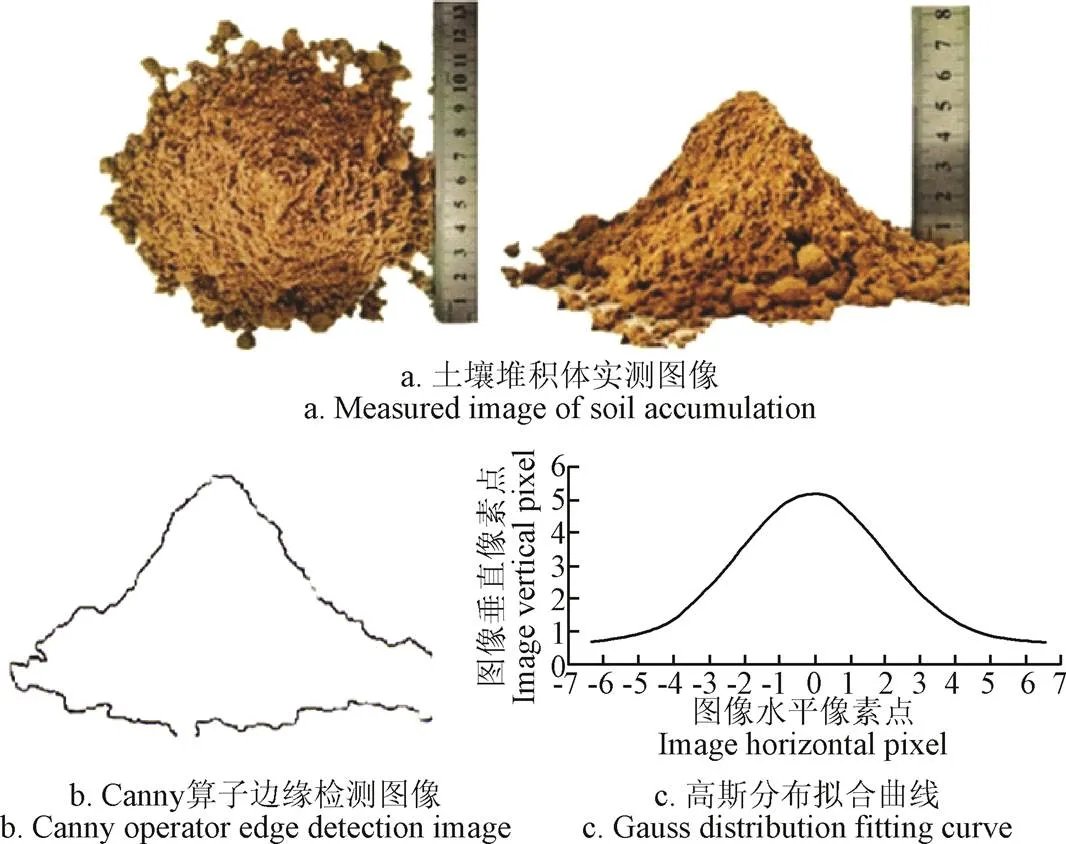
图7 土壤颗粒休止角计算过程
2.2 参数标定试验与结果
接触模型参数中没有显著性影响的参数并不能基于堆积角来标定。本文参照相关文献[22-26]的标定结果可知,颗粒间碰撞恢复系数、颗粒间静摩擦因数、颗粒间滚动摩擦因数以及颗粒间表面能4个因素对于堆积角的影响是显著的,所以标定结果可靠。进行堆积角Box-Behnken试验,试验因素为颗粒间碰撞恢复系数、颗粒间静摩擦因数、颗粒间滚动摩擦因数和颗粒表面能,分别对应、、、。设3组0水平试验,共进行27组试验,试验因素编码值与仿真试验结果如表7所示。使用State-East公司的Design-Expert V8.0.6.1软件对试验数据进行响应面分析,结果如表8所示,得到回归模型为
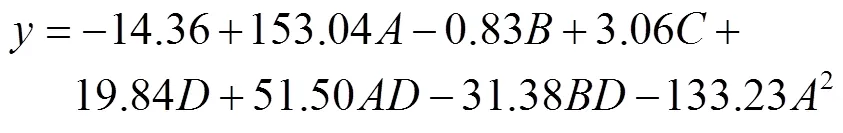
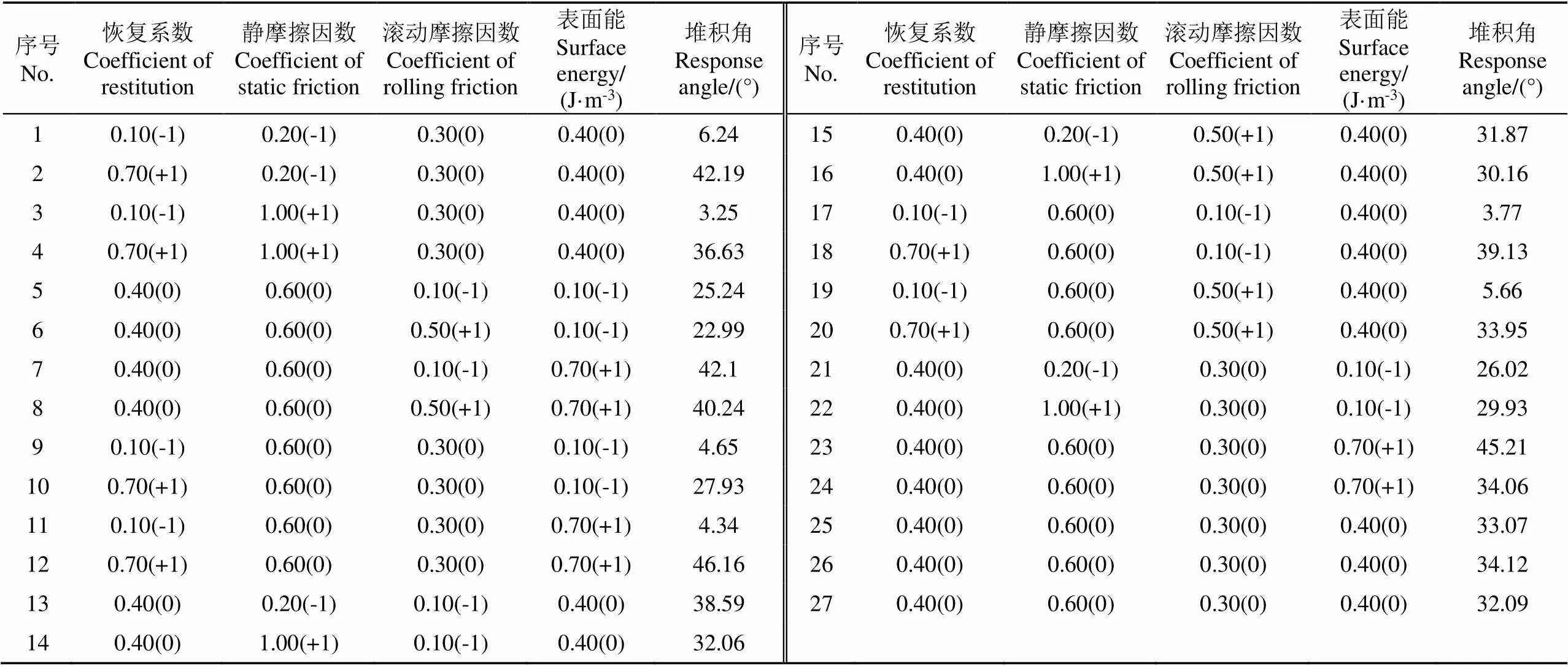
表7 堆积角仿真试验方案与结果
模型显著性检验<0.000 1,决定系数2=0.990 9,失拟项=0.207 5,说明回归模型极显著,失拟项不显著,拟合程度很高。由表8可知,对土壤堆积角的影响,、、、、、2极显著,显著、影响显著顺序为>>2>>>>。试验因素与堆积角之间存在二次非线性关系和交互作用。
对回归模型进行优化,以实际堆积角平均值为优化目标,颗粒间碰撞恢复系数、颗粒间静摩擦因数、颗粒间滚动摩擦因数、颗粒间表面能作为变量,建立参数优化数学模型,使用MATLAB软件的优化工具箱进行求解。结果表明当颗粒间碰撞恢复系数为0.42,颗粒间静摩擦因数为0.20,颗粒间动摩擦因数为0.30,颗粒间表面能为0.40J/m3时,仿真得到土壤堆积角数值为41.25°与实际堆积角平均值41.87°基本一致,误差为1.48%,如图8所示。
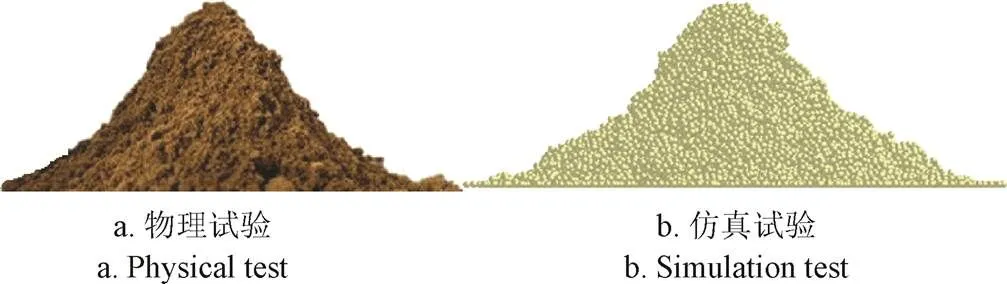
图8 优化解下的堆积角仿真试验与物理试验结果

表8 通用旋转组合设计回归方程方差分析
3 麻山药与钢板及沙壤土间接触参数的标定
麻山药根茎较长,在试验过程中截取形态较为均匀的圆柱形根茎段进行试验。在EDEM软件中使用颗粒填充法建立麻山药颗粒仿真模型[27], 仿真模型与实物对比如图9a所示。将安平县沙壤土均匀填入长500 mm、宽400 mm、高15 mm的无上盖铁盒中,并轻微压实,得到沙壤土土床。在EDEM软件中,使用上一节所测得沙壤土相关参数建立颗粒床,待颗粒完全静止后用平面轻微压实颗粒床,保证压实后颗粒床高度与实际土床高度基本一致,如图9b所示。
3.1 麻山药碰撞恢复系数测定
碰撞恢复系数的定义为碰撞后法向相对分离速度与碰撞前相对接近速度的比值[26,28],碰撞恢复系数的计算如式

式中H为麻山药下落高度,m;h为麻山药弹起高度,m。
为保证麻山药在下落后不会破裂同时弹起高度易于分辨,进行预试验确定麻山药下落最佳高度为700 mm。使用高速摄像机对试验过程录像,应用卷尺及钢板尺测量麻山药与铁板碰撞后弹起的高度,测量精度为5 mm。试验后,将录像视频进行0.1倍慢放,确定麻山药块弹起高度。分别试验10次后取平均值,得到麻山药-钢板之间的平均碰撞恢复系数为0.34,麻山药-沙壤土之间的平均碰撞恢复系数为0.21。在EDEM软件中进行仿真验证试验,麻山药仿真模型下落碰撞钢板、颗粒床后弹起高度与实际试验弹起高度平均值误差仅分别为0.64%、3.7%。
3.2 静摩擦因数仿真标定
利用斜面滑动法进行静摩擦因数的测定。使用数显角度尺测量倾斜角度,精度为0.05°,试验测得麻山药在钢板上产生滑动的平均角度为13.45°,在沙壤土土床上产生滑动的平均角度为20.30°。仿真过程中将滚动摩擦因数设为0,待麻山药颗粒完全静止后,钢板与沙壤土土床分别以0.5 °/s的速度定轴转动,直至麻山药颗粒开始滑动。按一定梯度调整静摩擦因数,得到仿真试验结果如表9所示。建立拟合方程分别为
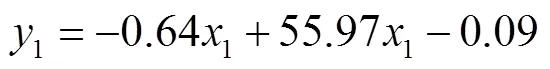

式中1、2分别表示麻山药颗粒在钢板、沙壤土表面开始产生滑动角度,(°);1、2分别表示麻山药-钢板、麻山药-沙壤土之间的静摩擦因数。
两拟合方程决定系数2分别为0.999 9、0.999 3,拟合程度较高。将1=13.45,2=20.30代入式中,得到麻山药-钢板间、麻山药-沙壤土间的静摩擦因数分别为1=0.26和2=0.38。进行仿真试验,得到仿真试样在钢板、颗粒床上开始产生滑动的平均角度分别为13.60°和20.85°,与实际试验误差分别为1.1%、2.6%。
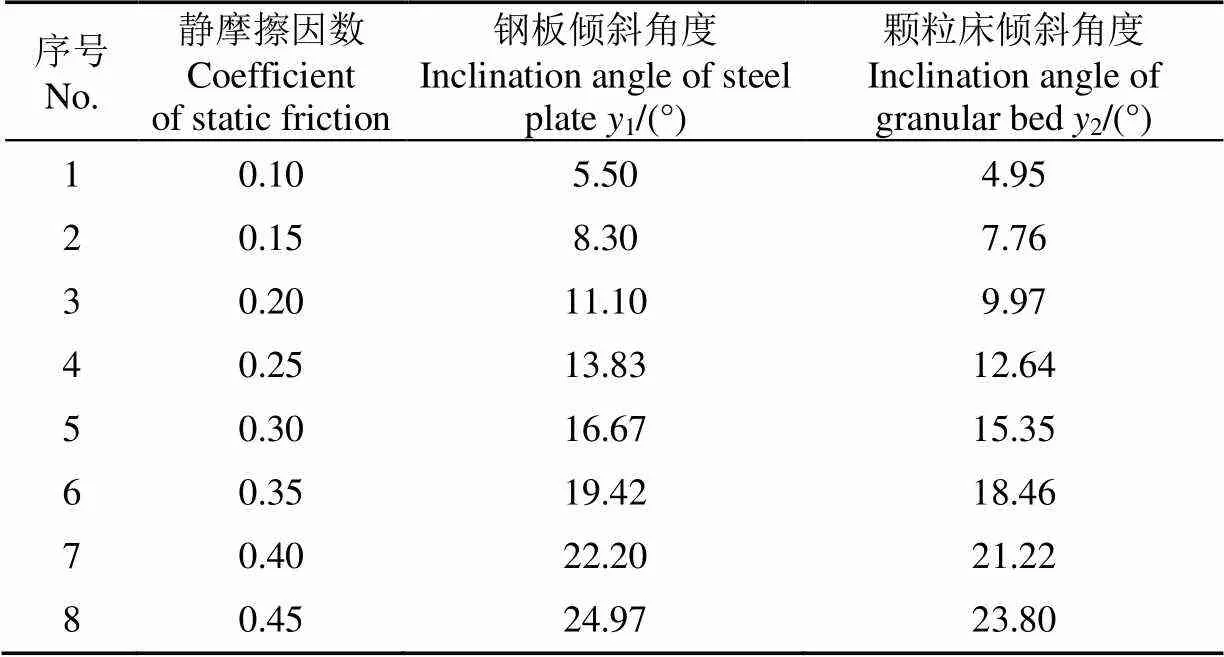
表9 静摩擦仿真试验方案与结果
3.3 滚动摩擦因数仿真标定
麻山药在钢板和沙壤土土床表面的滚动将产生滚动摩擦,试验中麻山药试样从一定倾斜角度的钢制平板上某一位置以初速度为0沿着斜面向下滚动(为减小土壤表面不够平滑所带来的试验误差,2次试验均用钢板作为倾斜板),最终分别滚落至水平放置的钢板和沙壤土土床上,滚动一段距离之后静止,采用卷尺测定麻山药块在水平钢板和沙壤土床表面的滚动距离,测量精度为5 mm,以滚动距离为评价指标,对麻山药-钢板和麻山药-沙壤土间的滚动摩擦因数进行测定。为保证麻山药在滚动过程中不会停置、产生弹跳以及滚出测试区域等情况,通过预滚动试验确定了斜置钢板倾斜角度为17°,在斜置钢板上滚动距离分别设为1=300 mm,2=200 mm。假设麻山药试样为一颗理想的圆柱体[3,23],将试验过程认定为纯滚动,不考虑静摩擦力的影响,由能量守恒定律得

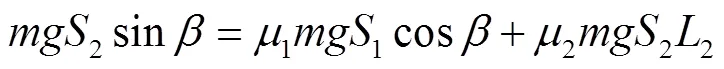
式中为钢板倾斜角度,(°);为麻山药块在倾斜刚板上的滚动距离,m;1为麻山药与钢板间的滚动摩擦因数,μ为麻山药与沙壤土间的滚动摩擦因数;L为麻山药在钢板上的滚动距离,m;2为麻山药在沙壤土表面的滚动距离,m。滚动摩擦试验结果如表10所示。将表中数据代入公式得到麻山药与钢板、麻山药与沙壤土之间的平均滚动摩擦因数分别为0.104、0.125。
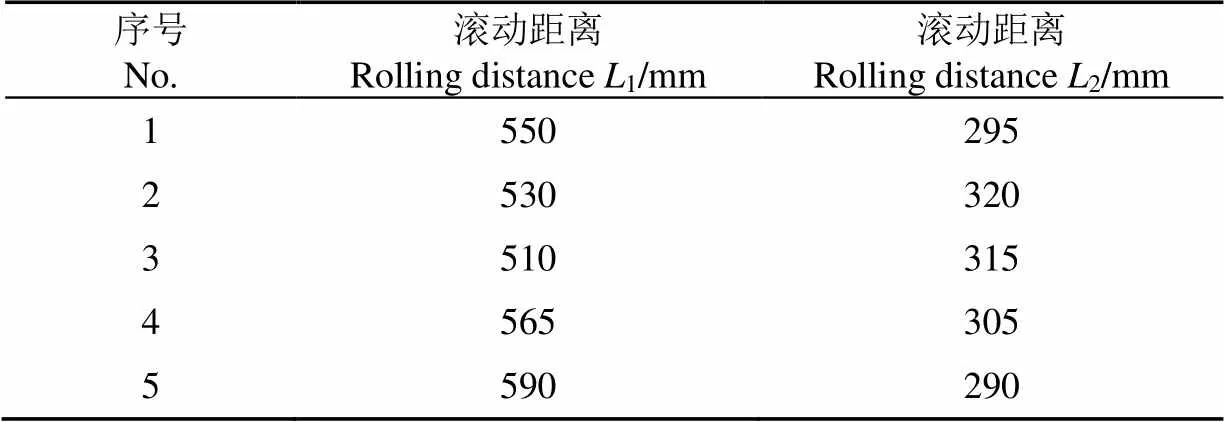
表10 滚动摩擦试验结果
沿倾斜钢板面向上距离底端1=300 mm、2=200 mm处进行麻山药颗粒仿真验证试验。仿真过程中发现,麻山药在钢板、土颗粒床上的平均滚动距离分别为549、305 mm,相比实际试验滚动距离平均值偏小。随后进行滚动摩擦仿真标定试验,按一定梯度调整滚动摩擦因数,试验结果如表11所示,建立拟合方程分别为


式中3、4分别表示麻山药颗粒在钢板、沙壤土表面的滚动距离,m;3、4分别表示麻山药颗粒-钢板、麻山药颗粒-沙壤土间的滚动摩擦因数。
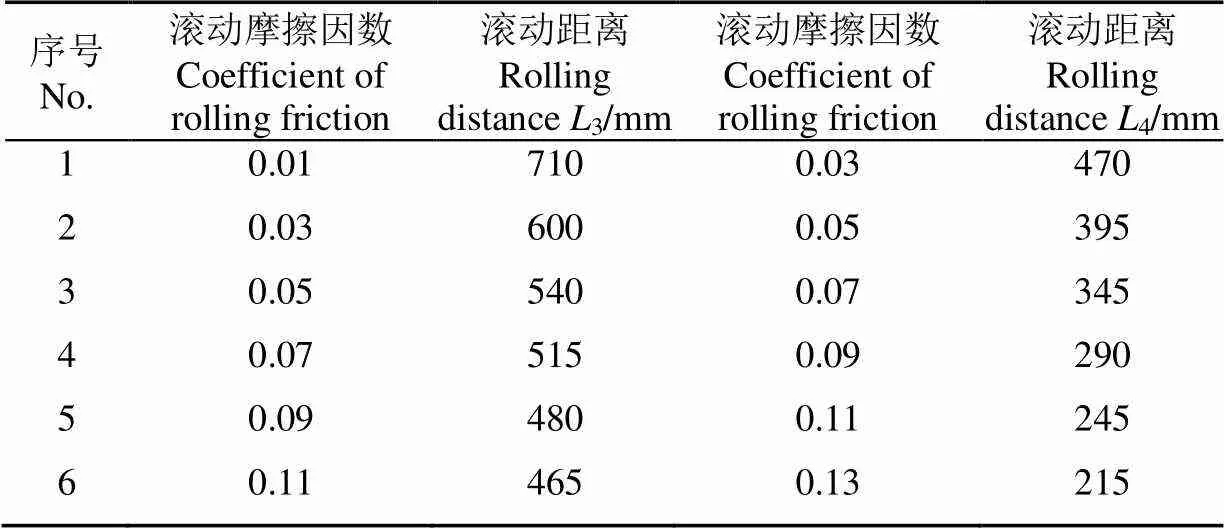
表11 麻山药颗粒滚动摩擦仿真试验方案与结果
方程决定系数2分别为0.986 3、0.998 8,拟合方程较为准确可靠。将实际试验滚动距离平均值分别代入两方程中,得到滚动摩擦因数3=0.049,4=0.075。对得到的参数进行仿真验证,重复5次试验得到平均滚动距离分别为558、320 mm,与实际试验滚动距离误差分别为1.60%、4.91%。
通过仿真标定试验得到麻山药与钢板、沙壤土间仿真滚动摩擦因数1=0.049、2=0.075,与实际试验滚动距离误差仅为1.60%和4.91%;而根据能量守恒试验法测得1=0.104、2=0.125,与实际试验相对误差较大,分别为112.25%、67%。原因可能是:真实麻山药并不是理想的圆柱体,同时所选取的麻山药颗粒表皮以及钢板表面特性与仿真模型有差异;在实际试验条件下麻山药重力势能的损耗并不完全来自滚动摩擦,还包括颗粒-钢板、沙壤土所产生的静摩擦以及颗粒在滚动过程中与钢板、沙壤土碰撞所损耗的能量,而假设理想试验将这些能量消耗所忽略,故出现以能量守恒法所测值与实际试验值相对误差较高的情况。因此,在进行滚动摩擦因数测定时,要充分考虑试验对象的特殊性,选用适宜的方法进行测定。
4 结 论
1)通过试验测得麻山药根茎的含水率、密度、弹性模量等本征参数,发现麻山药径向与轴向弹性模量值相差较小,表明其结构较为均质;根据所测参数建立了麻山药离散元双峰分布模型,并从表观和力学性能2个方面进行了验证,表明双峰分布模型能够较好的表征麻山药物理特性。
2)确定了安平县沙壤土堆积角度,结合Box-Behnken响应面分析试验建立并优化了麻山药种植区的沙壤土堆积角与颗粒间碰撞恢复系数、静摩擦因数、滚动摩擦因数及表面能4个显著性参数之间的回归模型,得到最优参数组合依次为0.42、0.20、0.30、0.40J/m3,为土壤模型的建立及麻山药与土壤接触参数的标定提供参考。
3)在EDEM软件中建立了麻山药仿真试样、钢板及颗粒床模型,通过将实际试验与数值模拟试验相结合,得到了麻山药与钢板的碰撞恢复系数、静摩擦因数、滚动摩擦因数分别为0.34、0.26、0.049,与沙壤土之间的碰撞恢复系数、静摩擦因数、滚动摩擦因数分别为0.21、0.38、0.075。为后续建立麻山药-沙壤土复合体模型提供了准确的数值参考,进而使麻山药收获过程实现可视化、参数化;同时标定结果可为麻山药产后加工的相关仿真试验及麻山药产业全程机械化进程的推进提供理论基础。
[1] 王国强,郝万军,王继新. 离散单元法及其在EDEM上的实践[M].西安:西北工业大学出版社,2010.
[2] 高国华,谢海峰,王天宝. 设施蔬菜收获机拉拔力学性能EDEM仿真与试验[J]. 农业工程学报,2017,33(23):24-31.
Gao Guohua, Xie Haifeng, Wang Tianbao. EDEM simulation and experiment of pullout force of protected vegetable harvester[J]. Transactions of the Chinese Society of Agricultural Engineering, 2017, 33(23): 24-31. (in Chinese with English abstract)
[2] 刘文政,何进,李洪文,等. 基于离散元的微型马铃薯仿真参数标定[J]. 农业机械学报,2018,49(5):132-142,149.
Liu Wenzheng, He Jin, Li Hongwen, et al. Calibration of simulation parameters for potato minituber based on EDEM[J]. Transactions of the Chinese Society for Agricultural Machinery, 2018, 49(5): 132-142, 149. (in Chinese with English abstract)
[3] 原建博,李骅,吴崇友,等. 基于离散单元法的水稻籽粒快速颗粒建模研究[J]. 南京农业大学学报,2018,41(6):187-194.
Yuan Jianbo, Li Hua, Wu Chongyou, et al. Study on apace particle modeling of rice grain basis on the discrete element method[J]. Journal of Nanjing Agricultural University, 2018, 41(6): 187-194. (in Chinese with English abstract)
[4] 张涛,刘飞,赵满全,等. 大豆种子与排种器接触物理参数的测定与离散元仿真标定[J]. 中国农业大学学报,2017,22(9),86-92.
Zhang Tao, Liu Fei, Zhao Manquan, et al. Measurement of physical parameters of contact between soybean seed and seed metering device and discrete element simulation calibration[J]. Journal of China Agricultural University, 2017, 22(9): 86-92. (in Chinese with English abstract)
[5] 程一启,张兆国,张丹,等. 三七收获机组合式挖掘铲减阻效果研究:基于EDEM[J]. 农机化研究,2019,41(2):55-60.
Cheng Yiqi, Zhang Zhaoguo, Zhang Dan, et al. Research of resistance reduction effect of panax notoginseng harvest combined digging shovel: Based on EDEM[J]. Journal of Agricultural Mechanization Research, 2019, 41(2): 55-60. (in Chinese with English abstract)
[6] 王笑丹,王洪美,韩云秀,等. 基于离散元法的牛肉咀嚼破碎模型构建[J]. 农业工程学报,2016,32(4):228-234.
Wang Xiaodan, Wang Hongmei, Han Yunxiu, et al. Structure of beef chewing model based on discrete element method[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(4): 228-234. (in Chinese with English abstract)
[7] 江涛,吴崇友,汤庆,等. 基于ANSYS和EDEM的小麦茎秆切割仿真研究[J]. 江苏农业科学,2018,46(17):231-234.
[8] Quist J, Evertsson C M. Cone crusher modelling andsimulation using DEM[J]. Minerals Engineering, 2016, 85: 92-105.
[9] 徐金明,谢芝蕾,贾海涛. 石灰岩细观力学特性的颗粒流模拟[J]. 岩土力学,2010,31(增刊2):390-395.
Xu Jinming, Xie Zhilei, Jia Haitao. Simulation of mesomechanical properties of limestone using particle flow code[J]. Rock and Soil Mechanics, 2010, 31(Supp.2): 390-395. (in Chinese with English abstract)
[10] Quist J. Cone Crusher Modelling and Simulation[D]. Gothenburg: Chalmers University of Technology, 2012.
[11] Mishra B K. A review of computer simulation of tumbling mill by the discrete element method: Part I-contact mechanics[J]. International Journal of Mineral Processing, 2003, 71(1/2/3/4): 73-93.
[12] 张涛,刘飞,赵满全,等. 基于离散元的排种器排种室内玉米种群运动规律[J]. 农业工程学报,2016,32(22):27-35.
Zhang Tao, Liu Fei, Zhao Manquan, et al. Movement law of maize population in seed room of seed metering device based on discrete element method[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(22): 27-35. (in Chinese with English abstract)
[13] 赖庆辉,袁海阔,胡子武,等. 滚筒板齿式三七种苗分离装置结构设计与试验[J]. 农业机械学报,2018,49(4):121-129.
Lai Qinghui, Yuan Haikuo, Hu Ziwu, et al. Design and experiment on seedling separation device of panax notoginseng seedlings based on roller zigzag mechanism[J]. Transactions of the Chinese Society for Agricultural Machinery, 2018, 49(4): 121-129. (in Chinese with English abstract)
[14] Yu Y, Fu H, Yu J. DEM-based simulation of the corn threshing process[J]. Advanced Powder Technology, 2015, 26(5): 1400-1409.
[15] 张锋伟,宋学锋,张雪坤,等. 玉米秸秆揉丝破碎过程力学特性仿真与试验[J]. 农业工程学报,2019,35(9):58-65.
Zhang Fengwei, Song Xuefeng, Zhang Xuekun, et al. Simulation and experiment on mechanical characteristics of kneading and crushing process of corn straw[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(9): 58-65. (in Chinese with English abstract)
[16] 霍丽丽,孟海波,田宜水,等. 粉碎秸秆类生物质原料物理特性试验[J]. 农业工程学报,2012,28(11):189-194.
Huo Lili, Meng Haibo, Tian Yishui, et al. Experimentalstudy on physical property of smashed crop straw[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2012, 28(11): 189-194. (in Chinese with English abstract)
[17] 刘凡一. 清选装置中小麦颗粒和短茎秆离散元建模研究[D]. 杨凌:西北农林科技大学,2018.
Liu Fanyi. Discrete Element Modelling of the Wheat Particles and Short Straw in Cleaning Devices[D]. Yangling: Northwest A&F University, 2018. (in Chinese with English abstract)
[18] 姚宗路,欧阳双平,孟海波,等. 颗粒状秸秆物料流动特性试验[J]. 农业机械学报,2012,43(7):112-116.
Yao Zonglu, Ouyang Shuangping, Meng Haibo, et al. Flow characterization of biomass particle straw[J]. Transactions of the Chinese Society for Agricultural Machinery, 2012, 43(7): 112-116. (in Chinese with English abstract)
[19] 毕秋实,王国强,陈立军,等. 基于离散元-多体动力学联合仿真的机械式挖掘机挖掘阻力仿真与试验[J]. 吉林大学学报:工学版,2019,49(1):106-116.
Bi Qiushi, Wang Guoqiang, Chen Lijun, et al. Numerical simulation and experiment on excavation resistance of mechanical excavator based on DEM-MBD co-simulation[J]. Journal of Jilin University (Engineering and Technology Edition), 2019, 49(1): 106-116. (in Chinese with English abstract)
[20] 张锐,韩佃雷,吉巧丽,等. 离散元模拟中沙土参数标定方法研究[J]. 农业机械学报,2017,48(3):49-56,343-350.
Zhang Rui, Han Dianlei, Ji Qiaoli, et al. Calibration methods of sandy soil parameters in simulation of discrete element method[J]. Transactions of the Chinese Society for Agricultural Machinery, 2017, 48(3): 49-56, 343-350. (in Chinese with English abstract)
[21] 罗帅,袁巧霞,GOUDA Shaban,等. 基于JKR粘结模型的蚯蚓粪基质离散元法参数标定[J]. 农业机械学报,2018,49(4):343-350.
Luo Shai, Yuan Qiaoxia, GOUDA Shaban, et al. Parameters calibration of vermicomposting nursery substrate with discrete element method based on JKR contact model[J]. Transactions of the Chinese Society for Agricultural Machinery, 2018, 49(4): 343-350. (in Chinese with English abstract)
[22] 夏鹏,李郁,杨公波. 散粒物料堆积角离散元仿真研究[J].起重运输机械,2015(2):107-110.
Xia Peng, Li Yu, Yang Gongbo. Study on the discrete element simulation of scattered materials[J]. Hoisting and Conveying Machinery, 2015(2): 107-110. (in Chinese with English abstract)
[23] 韩燕龙,贾富国,唐玉荣,等. 颗粒滚动摩擦系数对堆积特性的影响[J]. 物理学报,2014,63(17):4501-4507.
Han Yanlong, Jia Fuguo, Tang Yurong, et al. Influence of granular coefficient of rolling friction on accumulation characteristics[J]. Acta Physica Sinica, 2014, 63(17): 4501-4507. (in Chinese with English abstract)
[24] 贾旭光,陈曦,李鑫. 不同粒度和堆载形态下散体瞬时自然安息角的实验研究[J]. 现代矿业,2015,549(1):25-27.
Jia Xuguang, Chen Xi, Li Xin. Experiment research on instantaneous natural repose angle of granular slope under different granularity and stack form[J]. Modern Mining, 2015, 549(1): 25-27. (in Chinese with English abstract)
[25] 德颐姆科技有限公司. 含水率:物料参数中JKR表面能的设置[Z]. 深圳:EDEMBulkSim官方微博,2018[2018-04-09]. https://weibo.com/ttarticle/p/show?id= 2309404226950502699919.
[26] González-Montellano C, Fuentes J M, Ayuga-Téllez E, et al. Determination of the mechanical propertiesof maize grains and olives required for use in DEM simulations[J]. Journal of Food Engineering, 2012, 111(4): 553-562.
[27] 宋学锋. 基于离散元法的玉米秸秆揉丝机工作过程研究[D]. 兰州:甘肃农业大学,2018.
Song Xunfeng. Study on the Operation Process of the Corn Straw Kneading Machine Based on Discrete Element Method[D]. Lanzhou: Gansu Agricultural University, 2018. (in Chinese with English abstract)
[28] Zhou Y C, Xu B H, Yu A B, et al. Numerical investigation of the angle of repose of monosized spheres[J]. Physical Review E, 2001, 64(2Pt1): 021301.
Development of discrete element model and calibration of simulation parameters for mechanically-harvested yam
Hao Jianjun1, Long Sifang1, Li Hao1, Jia Yali2, Ma Zhikai1, Zhao Jianguo1
(1.,,071001,; 2.,050031,)
As the parameters of discrete element model for yam harvesting are difficult to obtain directly from literatures or experiments, this study proposes a parameter calibration method that combines experiments with numerical simulations. Firstly, a physical test was carried out. Compression, shear and bending tests were carried out on yam with the moisture content of 80%. The axial and radial elastic modulus of yam were obtained, which were 4.48 and 4.03 MPa, respectively. The results showed that the axial and radial elastic modulus were close, and the structure of yam was homogeneous. At the same time, the density, length and radial dimension of yam were measured. Based on the discrete element method, the bimodal distribution model of yam was established by the particle filling method. According to the research theories of domestic and foreign scholars, the bonding parameters of yam were calibrated. Through the compression and shear simulation tests in the discrete element software, the calibration parameters were checked and verified to make the calibration results more accurate. The experimental results showed that there were 9 887 non-equal size particles and 111 723 effective bonds in the bimodal distribution model of yam, the coordination number was about 11, the porosity was low, which could better characterize the mechanical properties of yam. The normal stiffness, shear stiffness, critical normal stress, critical shear stress and bonding radius were 9.3×105N/m, 3.0×106N/m, 0.58 MPa, 0.14 MPa, 3.5 mm. Secondly, the contact parameters of sand loam particles were calibrated by the soil accumulation angle test. The particle size of sandy loam was less than 4 mm, and the moisture content was 14.15%. After screening, the particles of sandy loam met the requirement of uniformity. The method of funnel test was used to form a certain stacking angle of sandy loam and the stacking body was photographed on the side. The acquired image was grayed and binarized by MATLAB and the edge was detected by Canny operator. Then the image was imported into Origin software to obtain the contour point coordinates. The scatter map was fitted with Gaussian distribution to find the inflexion point of the image and the sharp angle between the tangent of inflection point andaxis as the accumulation angle of soil was took. Then, several tests were carried out to determine the accumulation angle of sandy loam. Combined with the Box-Behnken response surface analysis test, the regression model between the sand soil accumulation angle and coefficient of restitution, coefficient of static friction, coefficient of rolling friction and surface energy was established and optimized. The optimal parameter combination was 0.42, 0.20, 0.30 and 0.40J/m3. The results showed that the average value of simulation soil accumulation angle was 41.25°, the average value of actual soil accumulation angle was 41.87°, and the error between them was only 1.48%. Finally, the simulation sample of yam, steel plate and particle bed model were established in EDEM software. Through the test of coefficient of restitution, static friction coefficient and coefficient of rolling friction, the coefficient of restitution, static friction coefficient and coefficient of rolling friction between yam-steel plate and yam-sandy loam were 0.34, 0.26, 0.049, 0.21, 0.38 and 0.075, the calibration results was reliable and accurate compared with the actual experimental errors of less than 5%. It provides accurate contact parameters for the subsequent establishment of composite model of yam and sandy loam, thereby we can visualize and parameterize the harvest process of yam; meanwhile, the calibration results can provide theoretical basis for the relevant simulation test of yam post-production processing and the promotion of the whole mechanization process of yam industry.
crops; models; discrete element method; yam; calibration of parameters
郝建军,龙思放,李 浩,贾雅丽,马志凯,赵建国. 机收麻山药离散元模型构建及其仿真参数标定[J]. 农业工程学报,2019,35(20):34-42.doi:10.11975/j.issn.1002-6819.2019.20.005 http://www.tcsae.org
Hao Jianjun, Long Sifang, Li Hao, Jia Yali, Ma Zhikai, Zhao Jianguo. Development of discrete element model and calibration of simulation parameters for mechanically-harvested yam[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(20): 34-42. (in Chinese with English abstract) doi:10.11975/j.issn.1002-6819.2019.20.005 http://www.tcsae.org
2019-08-15
2019-09-30
河北省现代农业创新团队建设项目(HBCT2018090206)
郝建军,教授,博士生导师,主要从事农机装备设计与制造研究。Email:hjjpaper@163.com
10.11975/j.issn.1002-6819.2019.20.005
S539; S313
A
1002-6819(2019)-20-0034-09
