一种基于小波包和主成分分析的超声信号特征提取方法
2019-12-19
(南昌航空大学 无损检测技术教育部重点实验室,南昌 330063)
超声检测技术具有检测成本低、灵敏度高等优点,被广泛应用于工业无损检测中。目前的超声检测技术中,对缺陷进行定性的方法还没有取得满意的效果[1]。在对缺陷信号类型的分析过程中,最重要的步骤就是提取缺陷信号的特征量。根据回波信号的时域幅值虽然能够判断出是否存在缺陷,但是仅仅从时域获得的缺陷信号信息是有限的。为了获得更多的表征缺陷信息的特征量,对信号进行频域分析也是非常有必要的[2]。
针对信号特征量的提取,相关人员进行了大量的研究。文献[3]提取A扫描数据作为特征量,并结合向量机对管道的缺陷进行了有效识别。文献[4]提取了缺陷信号的波峰时刻和幅值作为特征量,识别了不同类型的脱黏缺陷。文献[5]对信号进行EMD经验模态分解后,提取了IMF分量信号的最大幅值、中心频率和信号能量作为特征量以识别缺陷,取得了较好的效果。文献[6]对信号进行了小波包变换,从近似系数及细节系数提取样本的特征量,对复合材料进行缺陷识别,并证明了该方法能够进行有效分类。文献[7]以独立分量分析为基础,与瞬间态特征提取的特点相结合来进行信号特征提取,并取得了较好的效果。
笔者提出一种基于小波包分解及主成分分析的方法对缺陷信号进行分类。以铝板为例,提取了缺陷信号经过7层小波包分解后各个频段的能量占比作为特征量;结合PCA(主成分分析)对多维特征量进行降维,以累计贡献率达到90%及以上的特征值个数选取主成分个数得到融合特征量;最后将融合特征量输入BP神经网络系统进行缺陷分类,实现了对缺陷类型的识别。
1 小波包分解
小波包分解是一种使用小波基为基底信号,将信号f(t)表示为小波函数线性组合的方法。Mallet在多分辨率分析的基础上提出了正交小波变换分解与重构的快速算法,具体为:信号f(t)的N层小波包分解是将信号以尺度N变换到空间L2=(R)的两个正交子空间VN与WN上,由VN得到离散近似值cAN,由WN得到离散近似值cDN,下一层以尺度N+1继续将cAN分解到子空间VN+1和WN+1,不断分解下去,进行多分辨率分解[6]。
由于小波包分解不仅能够对信号分解后的低频分解系数进行分解,还能够对信号分解后的高频系数进行再分解,得到更精确的频谱成分,提供不同频段上信号的构成信息。所以不同类型的缺陷信号经小波包分解后, 在各频带的能量分布是不同的。针对不同类型的缺陷信号,对不同频率段的能量分布进行数值量化可以作为表征缺陷信息的特征[8]。
假设对缺陷信号进行7层小波包分解,可以将信号频率范围分解成128个频段。当前N个频段为信号能量分布的有效频段时,计算出小波包分解后第7层前N个频率段中每个频段的能量值所占第7层前N个频段总能量的比值,即可得到一个N维矩阵LN=(b1,b2,b3,…,bN)作为信号在频域内的特征量。
bi=xi/A7
(1)
式中:xi(i=1,2,3,…,N)为小波包分解后第7层中第i个频段的能量;A7为小波包分解后第7层前N个频段的总能量值。
2 主成分分析(PCA)理论
为了全面反映缺陷信号中包含的信息,需要提取多个特征值进行分析。但是特征值的数量过多会增加分类测试时的负担,且会对分析造成影响,所以在多维特征值中找到最能体现出缺陷信号差异的特征值,并将多维特征空间降维到低维特征空间是非常有必要的。
PCA的基本思想是将原数据进行重组[9-10],得到一组新的互不相关且相互独立的数据,来达到以较少的数据表现原数据特征信息的目的[11-12]。对于一组有N个指标的数据组,进行主成分分析后利用新的组合形式表征原数据组合,在所有的线性组合中选取方差Var(N)最大的组合称为第一主成分,记为Q1,当主成分Q1不足以表征原数据信息时,选取新的组合形式来补充表征原数据信息,称为第二主成分Q2,且Q2不应与Q1的信息重合,Q1与Q2满足COV(Q1,Q2)=0,依次类推直到主成分个数能够表征原信息特征。PCA分析步骤如下。
(1) 假设有一组样本记为K,首先对样本进行标准化处理得到标准化样本矩阵R。
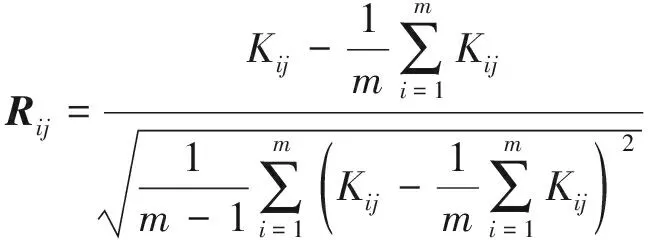
(2)
式中:i=1,2,…,m;j=1,2,…,n。
(2) 计算标准化样本的相关系数矩阵B
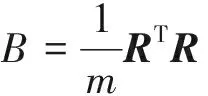
(3)
(3) 设特征值为λ,则可以计算出相关系数矩阵B的特征方程,由特征方程可以得到m个特征根。
|B-λIm|=0
(4)
根据计算出的特征值λi(i=1,2,3,…,m),可得到单位特征向量P1,P2,P3,…,Pm。
主成分个数,根据主成分累计贡献率来确定,对各主成分组合确定的数据矩阵及其矩阵的转置矩阵,求出协方差矩阵V及其特征值。主成分贡献率Ai,累计贡献率Cm可由式(5),(6)确定。
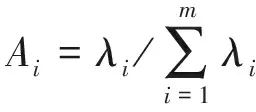
(5)
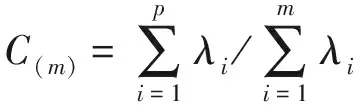
(6)
式中:p为确定特征值的个数。
当主成分累计贡献率大于90%时,此处可认为前p个主成分组合包括了原数据的大部分特征信息。对应的P就是前p个主成分[13]。
3 试验过程与分析
3.1 特征量的提取
试件为一块铝板,在板表面人为加工3类缺陷:10 mm×5 mm 的长方形裂纹(缺陷1)、直径为10 mm的孔洞(缺陷2)及直径为20 mm的孔洞(缺陷3)。试验装置由JPR-600C高功率信号发射接收器、外置信号放大器、电脑、扫查架、数据采集卡、铝板和空气耦合超声探头组成。其中,空气耦合超声探头中心频率为400 kHz,晶片尺寸(长×宽)为14 mm×20 mm,采样频率设置为5 MHz,采样数据点为1001个。将空气耦合超声发射探头与接收探头的角度设置为8.8°,并采用透射回波检测方式将探头在铝板同侧对向放置。
使用JPR-600C信号发射接收器发射电压为180V(峰峰值),周期数为7的矩形脉冲波激励空气耦合超声探头。空气耦合超声探头在无缺陷区域以及3种不同类型的缺陷区域试验时,接收到的波形如图1所示。
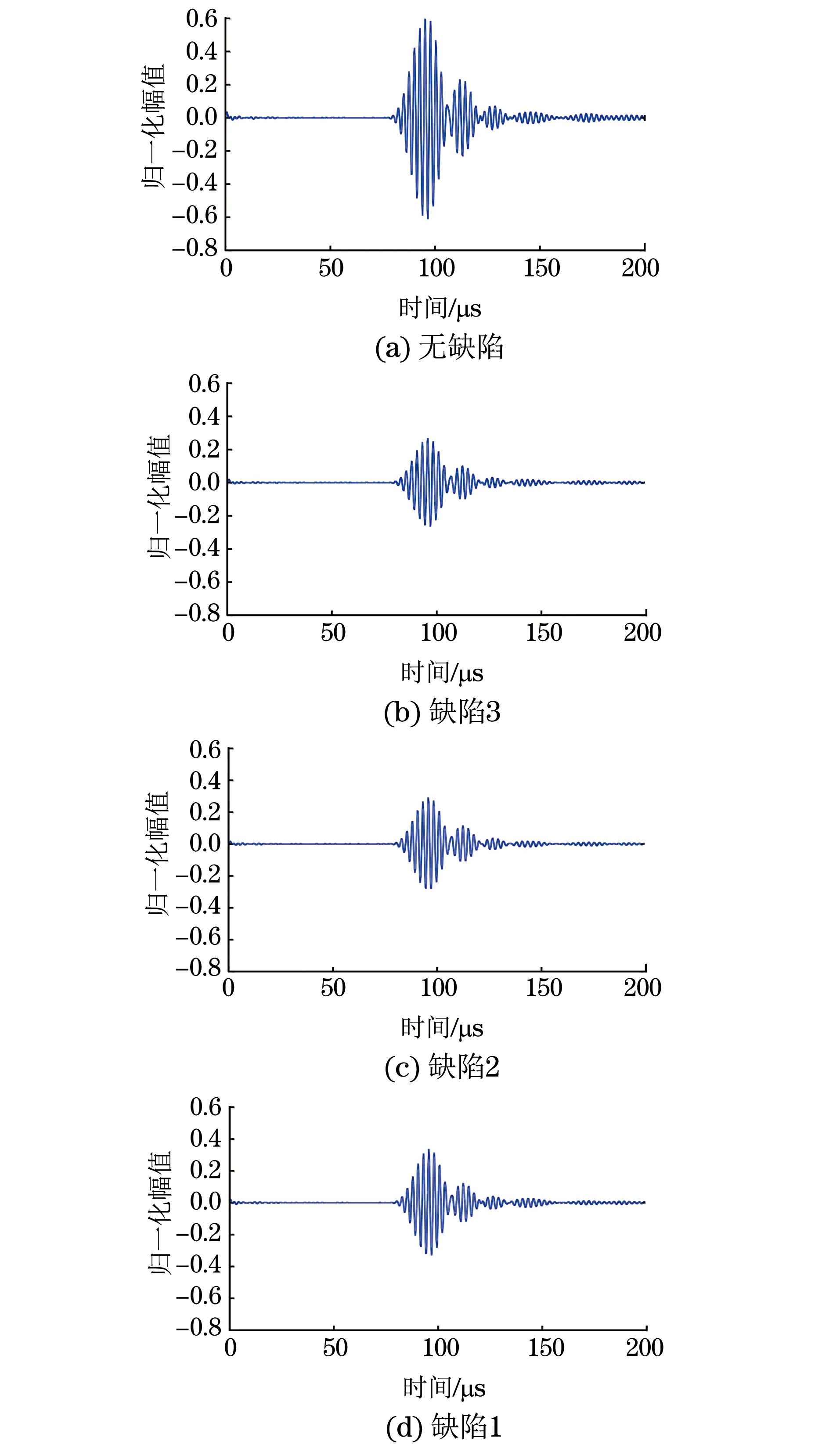
图1 无缺陷区域接收信号以及3种不同类型的缺陷信号
对比图1中3种类型的缺陷兰姆波信号,从时域幅值方面来说无明显区别,不足以对缺陷类型进行识别。接下来使用db9小波基对3种缺陷信号进行小波包7层分解,分解后可得到128个频段,提取第7层中前30个频段的能量值,并由式(1)计算出每个频段所占总能量的比值作为缺陷信号在频域内的特征量,3种缺陷前30个频段的能量占比分布如图2所示。
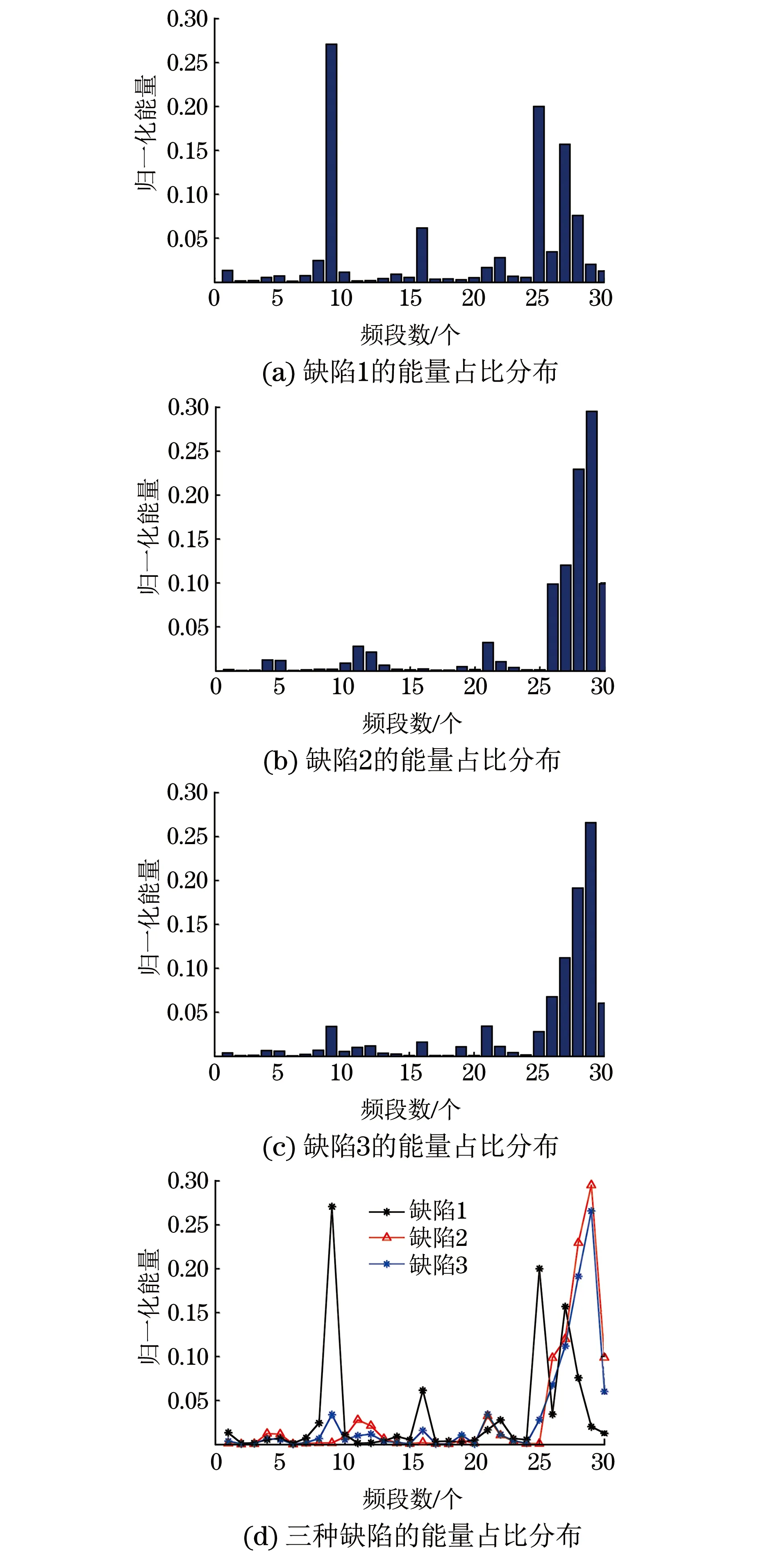
图2 3种缺陷的能量分布直方图
从图2可知,3种缺陷在前30个频段内的能量分布明显存在差异,说明频段能量分布可以作为区分缺陷类型的特征量。根据对缺陷信号提取的频段能量占比,每个缺陷信号最终可以得到30个特征量。对此3种缺陷共取150个信号(各缺陷分别取50个)进行同样的特征量提取,最后可以得到一组150×30的联合特征量矩阵。为了提高数据的分析效率以及降低数据信号的冗余度,使用PCA主成分分析方法对联合特征量矩阵进行降维处理得到融合特征量。首先根据式(2)将数据标准化预处理,然后根据式(3)~(6)分别得出其相关系数矩阵、特征值、对应的特征向量、特征贡献率和特征累计贡献率。最后将其全部特征值按由大到小的顺序依次排列,并根据特征累计贡献率大于90%的特征值个数便可得到特征向量的主分量。缺陷1信号特征量的前5个主成分特征值、贡献率和累计贡献率如表1所示。
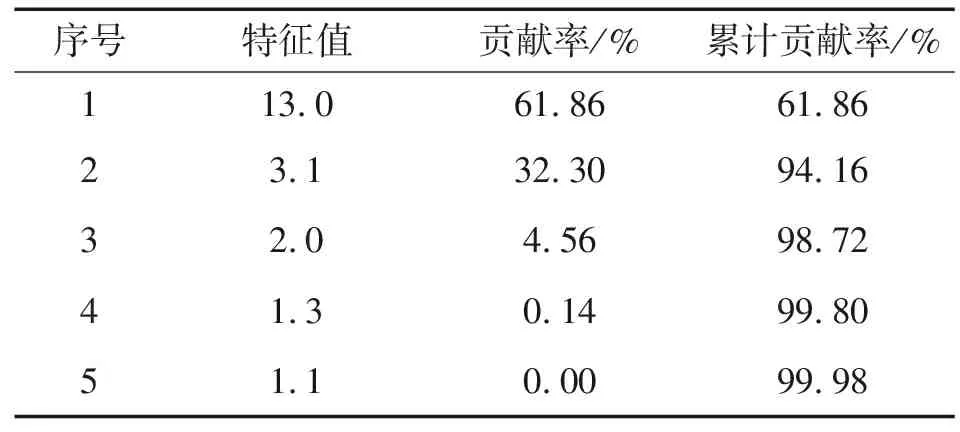
表1 缺陷1信号特征量的前5个主成分特征值
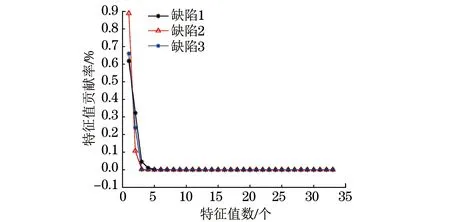
图3 3种缺陷的特征值贡献率
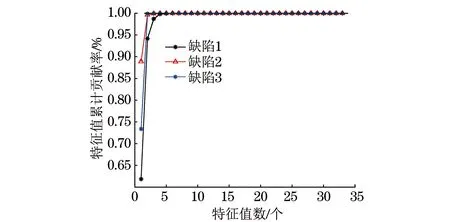
图4 3种缺陷的特征值累计贡献率
从图3所示的特征值贡献率可知,随着主成分特征值数量的增加,其特征贡献率越来越低,这说明各个主成分特征值能够表征3种缺陷信息的能力越来越低。为了避免信息冗杂,提高信号类型识别率,结合图4所示的3种缺陷累计贡献率可知,当特征值的数量达到2个时,其累计贡献率就已经达到了90%,这说明前2个特征值就已经能够表征3种缺陷信号的大部分信息。所以选取前2个主成分来组合得到一个150×2的融合特征量矩阵。
3.2 结果分析
针对150组数据进行PCA降维后获得的特征融合量,以及未经PCA处理的联合特征量,分别取缺陷1信号30组,缺陷2信号30组,缺陷3信号30组组成训练样本,剩下的60组样本组成测试样本。将缺陷1、缺陷2和缺陷3的信号特征融合量进行类型编码,3种类型的编码分别为100、010和001。将样本归一化后输入BP神经网络进行训练和识别。文章构建的BP神经网络的具体结构为:输入层、隐含层及输出层[2],包括的神经元个数分别为2,10,3。选取函数log-sigmoid作为神经网络传递函数,训练次数设为1 000次,训练误差值为0.01。经过神经网络训练后,未经PCA处理的联合特征量经过380步训练达到了性能参数要求,PCA处理后的融合特征量经过97步训练就已经达到了参数要求,测试结果如表2所示。
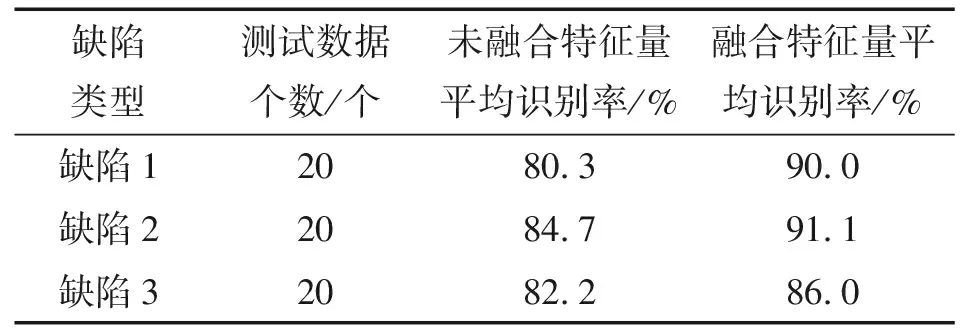
表2 3种缺陷的分类结果
从表2可知,提取小波包分解后的频段能量分布作为识别缺陷信号特征量的方法是可行的,且经过PCA处理后,BP神经网络对缺陷信号的识别率明显得到了提高,且测试速度更快。
4 结论
提取小波包多层分解后的频段能量作为特征量,结合PCA主成分分析法对特征量进行降维融合,去除冗杂信息,最后输入BP神经网络对缺陷进行了分类测试。试验结果表明,该特征量提取的方法能够有效地识别出缺陷信号的类型,且经过PCA处理后的特征量的分类测试精度和速度都明显得到了提高。
