基于CIVA仿真的电涡流检测参数优化
2019-12-19陈健飞1于成龙王安泉3周先军
陈健飞1,于成龙,王安泉3,周先军
(1.中国石化股份胜利油田分公司技术检测中心,东营 257000;2.中国石油大学(华东) 机电工程学院,青岛 266580;3.胜利油田检测评价研究有限公司,东营 257000)
涡流缺陷检测是指利用电磁感应原理,通过测量被检工件内感生涡流的变化来确定缺陷的无损检测方法。为提高涡流检测的效率,国内外研究学者做了大量的研究,诸如通过有限元分析、理论推导等方法对传感器的部分参数进行优化[1-8],但还是缺乏整体、系统的参数研究。笔者运用了CIVA仿真软件,通过设计合适的正交实验,较为全面地分析了不同影响因素发生变化时对最终结果的影响,并总结了不同因素的影响显著性程度以及对结果波动的贡献率大小,最终提出了最优的探头尺寸参数,以及实际调试过程中不同参数的推荐调试顺序。
1 电涡流传感器CIVA软件仿真模型
CIVA软件作为新兴的无损检测仿真软件,同传统的有限元仿真软件相比,更为专业,操作更为简洁。待测板材的材料参数如表1所示。
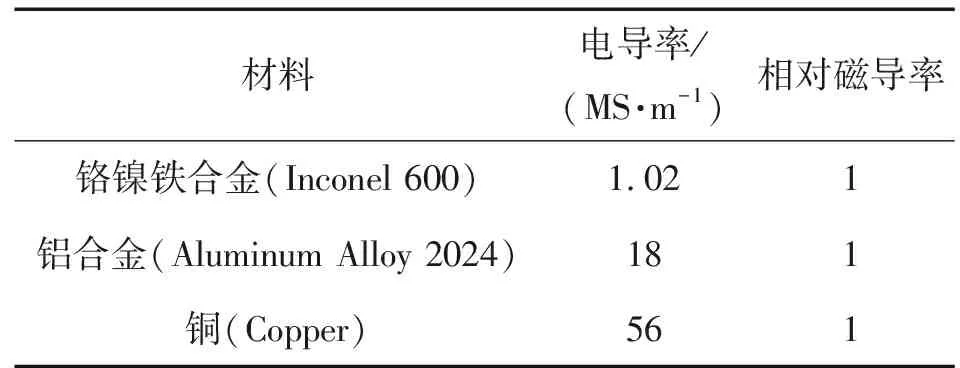
表1 待测板材材料参数
试验时,运用CIVA软件中的检测模拟模块(3D),被测试件是尺寸(长×宽×厚)为100 mm×100 mm×10 mm的板材,采用5 mm×0.2 mm×1 mm (长×宽×深)的缺陷来模拟裂纹,缺陷位置位于板材表面,探头位于板材有缺陷的表面一侧。采用CIVA软件中BEM方式下的自由划分模式进行缺陷网格划分,具体划分如图1(a)所示。
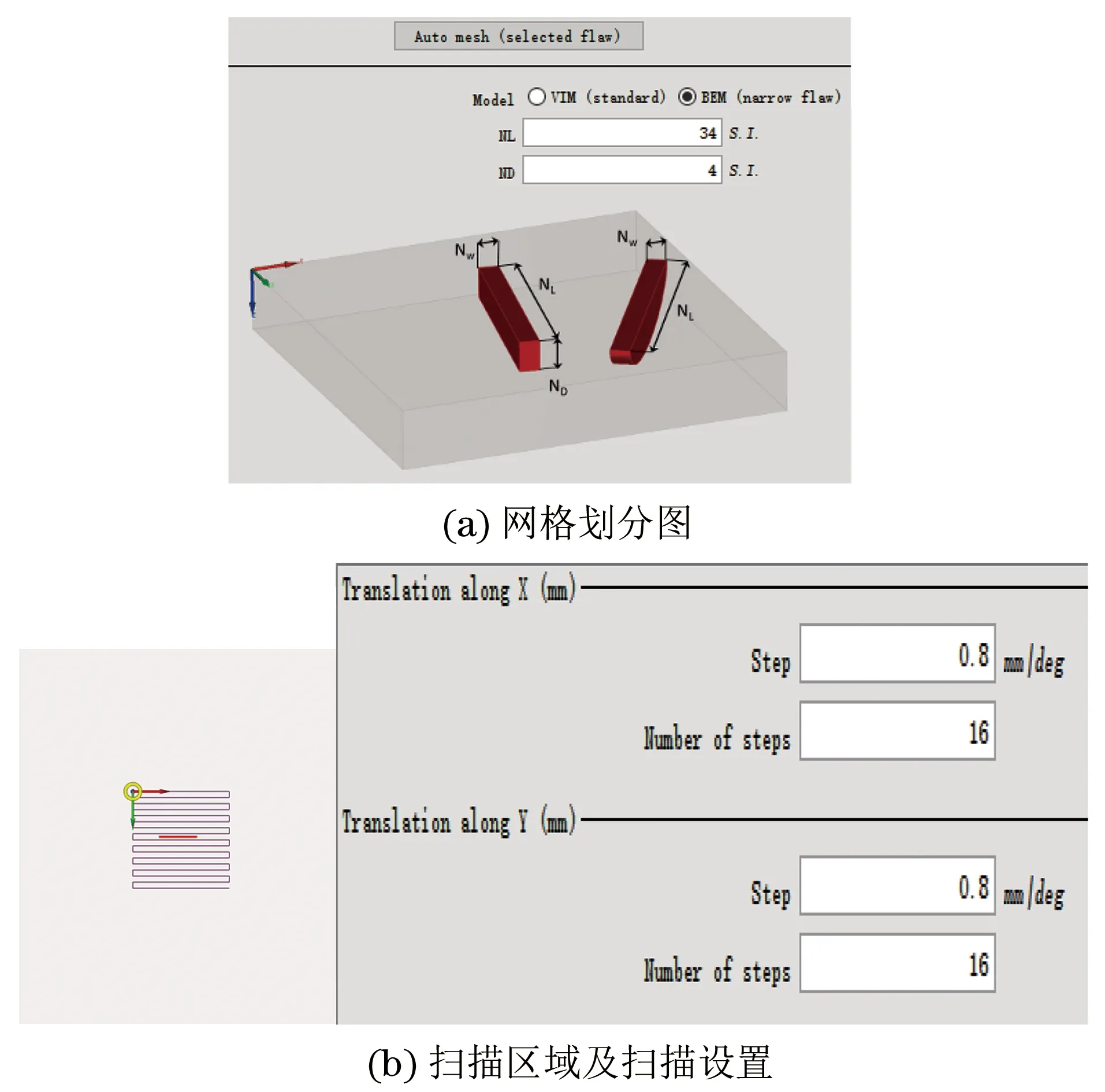
图1 仿真模型的网格划分图与扫描区域及扫描设置
探头采用普通圆柱形线圈(不含铁磁芯),线圈与板材间设置为空气域,探头的扫描方式采用栅形方式,步数及步长如图1(b)所示。扫描需要确保扫描区域覆盖缺陷区域。更改相关的检测参数[9-10],通过模拟仿真得出响应电压幅值来评价缺陷检测的敏感度,响应电压幅值越大表明对缺陷越敏感。最终的仿真模型及模拟结果如图2所示。
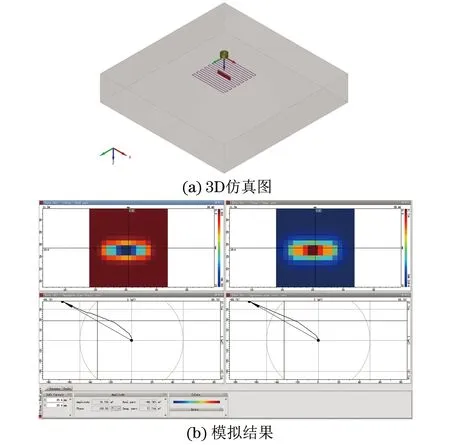
图2 仿真模型及模拟结果
2 正交实验
正交实验设计法可实现对多个影响因子和水平的考察。笔者先选取合适的影响因子和水平,确定合适的正交表并完成实验,最后通过直观分析法,方差分析法及贡献率分析法对实验数据进行分析[11]。
2.1 探头因素影响
针对与探头相关的影响因素,在不考虑各因素之间交互作用的前提下,考虑5因子5水平正交实验,选用L25(56)正交表,因子水平表如表2所示。
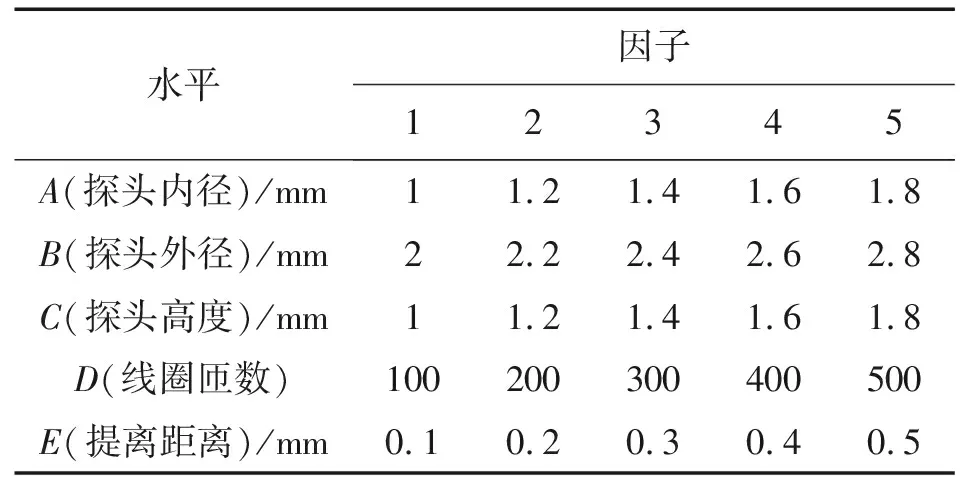
表2 探头因子水平表
用正交表L25(56)安排的实验共有25个不同水平的组合,在这些水平组合之下,保持激励频率500 kHz,激励电流100 mA不变,进行实验。实验完成后,统计各实验的响应电压幅值,响应电压幅值越大,代表对缺陷越敏感,实验结果越好。
(1) 铬镍铁合金(Inconel 600)板结果分析
对25次缺陷检测实验仿真结果(响应电压幅值的平均值)的直观分析计算结果如表3所示。
从表3可以看出,对铁合金板而言,最优的水平组合为A4B5C2D5E1,其与25个实验中最好的水平组合A3B5C2D4E1(15号实验)有所不同,所以增加了最优组实验,模拟得到A4B5C2D5E1组合下的响应电压幅值为2 736.66 mV,大于15号实验1 553.67 mV的响应电压幅值,进一步确定优方案为A4B5C2D5E1。对于铁合金板的缺陷检测,最主要的影响因子为D(线圈匝数),其次是E(提离距离),而该实验中的极差最小,说明实验误差较小,实验可靠性高。
铁合金板方差分析结果如表4所示(表中*代表在显著性水平0.01上是显著的,**代表在显示性水平0.05上是显著的)。
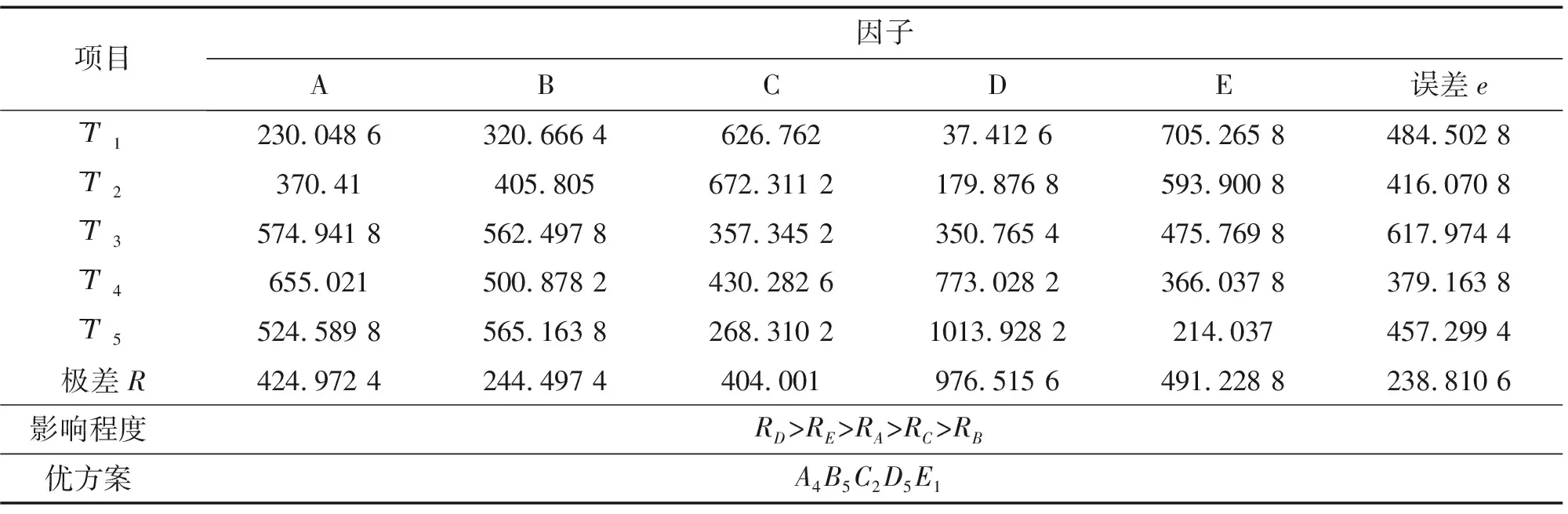
表3 铁合金板直观分析计算结果
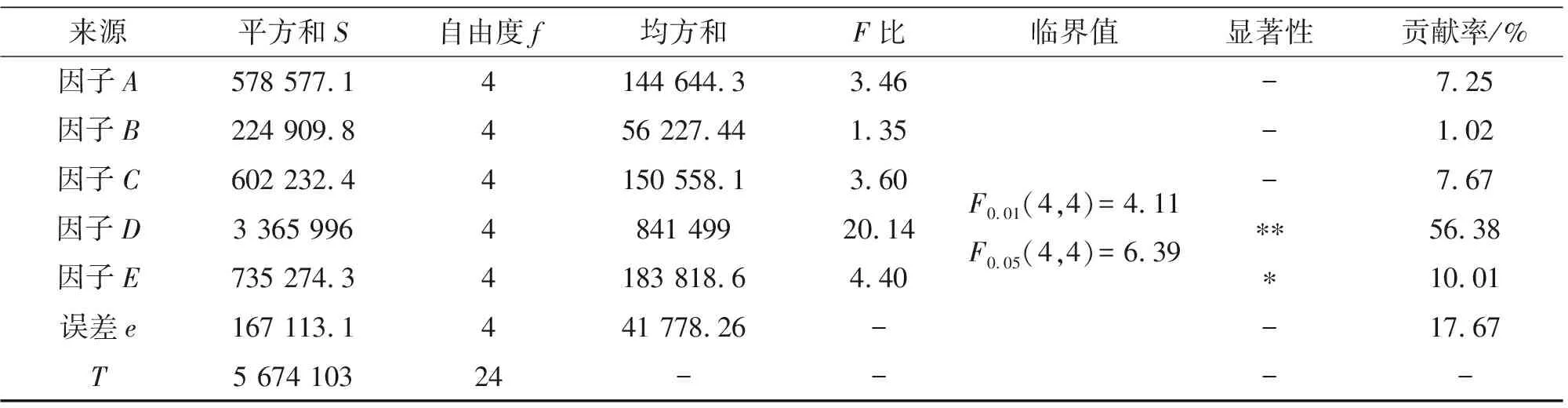
表4 铁合金板方差分析结果
从方差分析表可以看出,FD>F0.05(4,4)=6.39,FE>F0.01(4,4)=4.11,因子D与因子E分别在显著性水平0.05和0.01上是显著的,其他因子则不够显著。贡献率的数据同样说明了因子D与因子E对实验结果的影响较大,贡献率分别为56.38%和10.01%,因子A、B、C的贡献度较小,而因子B的贡献更是仅占到了1.02%,故可认为因子A、B、C相对而言不重要。
(2) 铝合金(Aluminum Alloy 2024)板结果分析
对铝合金缺陷板,重复上面的正交实验方法进行实验,同样运用直观分析法进行分析,得到优方案为A4B3C2D5E1,影响程度为RD>RE>RA>RC>RB。在优方案条件下进行实验,得到的响应电压幅值为2 482.144 mV。
方差分析法得到各因子的F比为:FA=4.27,FB=1.47,FC=4.23,FD=24.52,FE=6.47,同铁合金板相比,因子D更加显著,而因子E愈加趋近于显著性水平0.05的临界值。各因子的贡献率分别为:A,7.80%;B,1.12%;C,7.69%;D,56.04%;E,13.05%;误差e,14.30%。从贡献率分析,因子D最为重要,同铁合金板相比,因子E的贡献率开始提高,误差的影响开始减小。
(3) 铜(Cooper)板结果分析
同理可得到铜缺陷板的正交实验结果,直观分析法得到的优方案为A4B3C2D5E1,因子的影响程度为RD>RE>RA>RC>RB,同铝合金缺陷板相比,其在优方案与因子的影响程度上,基本无变化。在优方案A4B3C2D5E1条件下进行实验,得到的响应电压幅值为2 454.78 mV。
方差分析法得到各因子的F比为:FA=4.74,FB=1.68,FC=4.59,FD=26.26,FE=7.25,各因子的贡献率分别为:A,8.21%;B,1.50%;C,7.90%;D,55.48%;E,13.73%;误差e,13.18%。同铁合金与铝合金板相比,铜板随着材料电导率的增加,因子D(线圈匝数)的贡献率越来越小,因子E(提离距离)的贡献率越来越大。
(4) 小结
通过正交实验,得到不同材料缺陷板的检测最优探头参数如表5所示。
综上所述,对不同材料检测时,探头的尺寸参数受实际情况影响,本身可改变的范围较小,所以在模拟时,探头的尺寸参数对最终结果的影响较小。另外,线圈匝数的增加会使感应磁场增强;提离距离越小,电涡流的强度越大。优方案中,线圈匝数取最大值以及提离距离取最小值也是符合实际理论的。在实际应用时,应结合精度需求与实际工况,尽量取大的线圈匝数以及小的提离距离。

表5 不同材料缺陷检测探头的最优参数表
2.2 其他因素影响
确定探头的尺寸参数,使内径为1.6 mm,外径为2.4 mm,高度为1.2 mm,线圈匝数为300。考虑3因子3水平正交实验,选用L9(34)正交表,因子水平表[12-15]如表6所示。
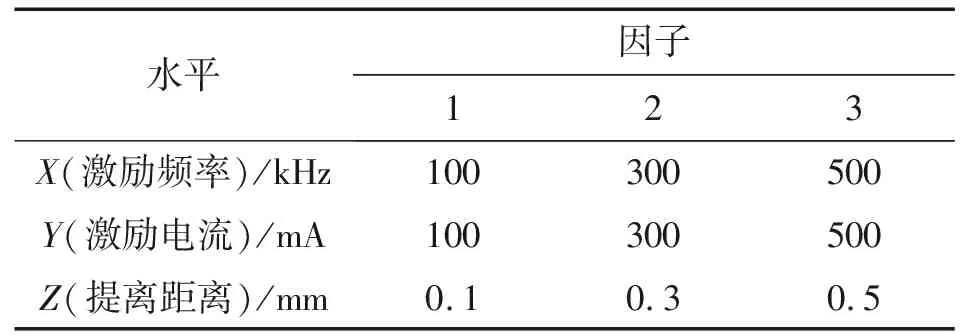
表6 因子水平表
对铁合金的直观分析结果(响应电压幅值的平均值)如表7所示。
从表7可以看出,对于激励频率与激励电流值应该尽量取大,提离距离尽量取小,提离距离的选择对应了探头因素实验中提离距离的选择。从直观分析可以看出,影响程度RX>RY>RZ。对于铝合金与铜板的直观分析,结果基本上与铁合金板的相同,优方案取X3Y3Z1,因子间的影响程度大小也相同,同样为RX>RY>RZ。
对铁合金的方差分析结果如表8所示。

表7 铁合金板直观分析结果
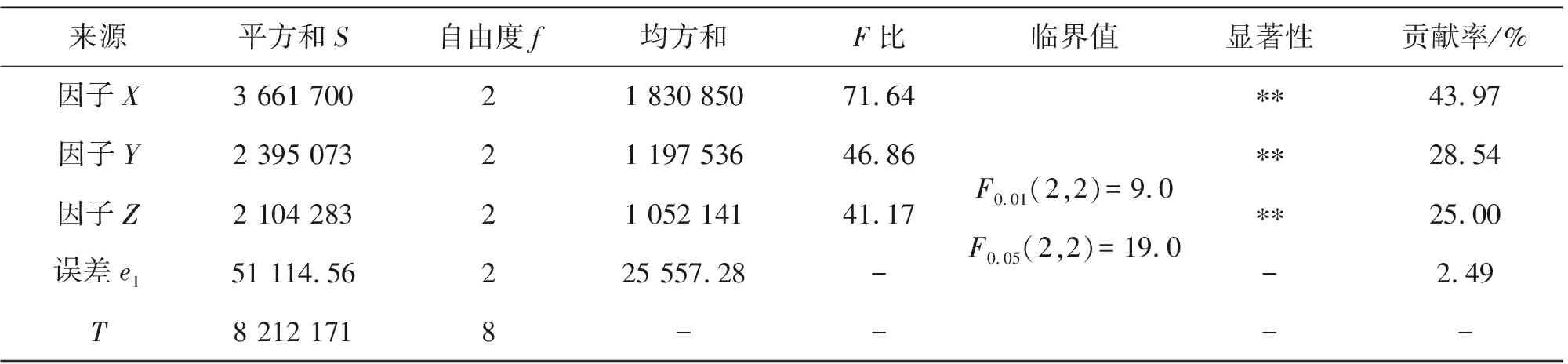
表8 铁合金板方差分析结果
从表8可以看出,因子X、Y、Z同样在0.05显著性水平上显著,各因子的贡献率也分别达到了43.97%,28.54%和25.00%,误差e1的贡献率相比其他因子的小,可以认为误差在此次实验中起到的作用可以忽略。对铝合金板与铜板的方差分析结果基本相同,两次试验的各因子同样在0.05显著性水平上显著。铝合金板各因子的贡献率分别为:因子X,31.18%;因子Y,34.28%;因子Z,32.92%;误差e1,0.6%。对于铜板,各因子的贡献率为:因子X,29.37%;因子Y,34.93%;因子Z,34.25%;误差e1,1.45%。随着被测工件电导率的增大,因子X(激励频率)的贡献越来越小,因子Y(激励电流)和因子Z(提离距离)的贡献越来越大,提离距离贡献率的增大验证了之前的实验结果。
不同材料时,各影响因子对检测结果的贡献度如图3所示。
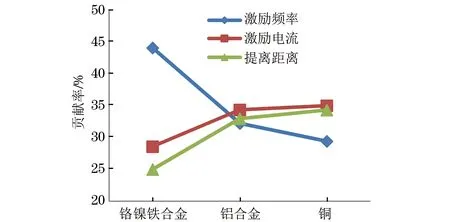
图3 不同材料时,各影响因子对检测结果的贡献率
综上所述,在实际测试中,为使设备最快达到最佳测试状态,各参数的调节先后顺序为:对于铁合金板为因子X,Y,Z;对于铝合金板,为因子Y,Z,X;对于铜板,为因子Y,Z,X。
3 结论
(1) 基于电涡流方法对金属板进行检测时,探头自身的尺寸参数相对其他参数,其可调节的范围不大,对检测结果影响的贡献率相对较小;而调节较为方便的激励频率、激励电流、提离距离等参数,对最终结果影响的贡献率较大。在实际测量中应根据实际情况选择较大的激励频率、激励电流、线圈匝数以及较小的提离距离。
(2) 随着被测试件电导率的增加,对检测结果影响比较大的几个因素中,激励频率与线圈匝数的贡献率越来越小,激励电流与提离距离的贡献率越来越大。在实际检测时,可优先调节贡献率大的参数,以节省调参时间。
(3) 在其他影响参数确定的情况下,探头内径与探头高度对最终结果的影响较大,在文中正交实验给出的探头尺寸参数中,可优先选择探头内径为1.6 mm,探头高度为1.2 mm的尺寸,而探头外径与这两者相比,贡献度较小,可认为不重要,可根据实际情况适当选择。
