一种基于惯导/地磁信息融合的 低成本组合导航方法

王伟东，李 革，刘佳琪，刘 鑫，马 凯

（1. 北京航天长征飞行器研究所，北京，100076；2. 试验物理与计算数学国家重点实验室，北京，100076）

0 引 言

在飞行器导航中，最早应用的导航方法是惯性导航，基本原理是利用惯性器件测量载体运动参数，通过数据处理获取飞行器当前的位置、姿态等信息。而惯导系统由于惯性器件本身带有的测量漂移误差，其误差会随时间累积，不适合长时间导航任务。为实现空间在轨飞行器长时间精确导航，通常采用高精度传感器，如星敏感器和光纤陀螺仪等[1]，但其体积大、功耗高、成本高，难以在低成本飞行器上得到广泛应用。地球磁场稳定性高、变化较慢、精度适中[2]，惯性/地磁组合导航已应用于船舶、潜艇、巡航导弹等领域导航[3～8]。但由于地磁导航系统（Geomagnetic Navigation System，GNS）的精度主要取决于惯性器件、地磁匹配图、地磁测量设备等的精度和计算机解算速度因素，目前尚未达到轨道飞行器高速动态导航要求[9]。

本文针对短时间在轨小型飞行器，提出了一种基于低成本惯导/地磁敏感器件的信息融合组合导航方法，通过利用微机电系统（Micro-Electro-Mechanical System，MEMS）惯性组合和磁强计输出参数共同构建状态方程和量测方程，并采用基于反馈校正的卡尔曼滤波算法，分析了高、中、低精度的惯导组合和MEMS 三轴磁强计不同测量精度条件下的导航精度偏差，结果表明采用惯导/地磁信息融合导航，可降低对惯性器件的精度要求，从而降低了轨道飞行器导航的经济、质量成本和对安装空间的需求。同时继承了惯性组合仅依靠自身传感器，不与外界发生信息交换的优点，具有广泛的应用前景。

1 MEMS 三轴磁强计与加速度计组合测量姿态原理

在飞行过程中，飞行器姿态变化导致三轴微磁传感器感应到的地球磁场矢量在其各轴上的投影分量发生变化；信号采集与处理模块进行信号变送和调理，传输给微处理器中解算出姿态信息。

定义载体坐标系，纵轴为X 轴，向右为Y 轴，Z 轴为符合右手定则的方向。定义地磁坐标系，磁北为X 轴，重力方向为Z 轴，Y 轴为符合右手定则的方向。将三轴磁强计和三轴加速度计沿载体坐标系安装，重合时，如果载体处于静止或者匀速运动状态，则加速度计的测量输出ta 为

式中 g 为重力加速度。如果载体处于任意姿态，则 加速度计的测量输出为

式中xa ，ya ，za 为ta 在X 轴、Y 轴、Z 轴的分量。

由欧拉角的旋转关系可以得到如下转换（3-2-1 的旋转顺序）：

式中 θ ，ψ ，γ 分别为俯仰角、偏航角和滚转角。

从式（3）中可以得到俯仰角和滚转角：

因此，在载体静态或者匀速运动的状态下，单独利用加速度计并不能得到完整的3 个姿态角，需要利用磁强计的信息，才能得出全部的欧拉角。

假设已知当地地磁场强度为M ，磁倾角为η，这样的信息可以事先得到，三轴磁强计的输出为

由式（5）得到的航向角为

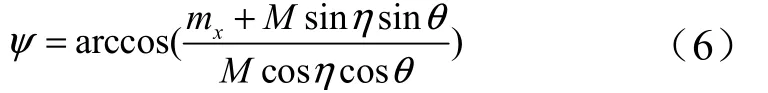
微磁传感器通过敏感地磁场，利用已知的地球磁场空间分布可实现载体的姿态测量。此方案在无磁干扰环境中有很好的应用效果，难点在于存在强磁背景环境或变化软磁环境下，由磁信息解算姿态存在较大误差。对于空间应用来说，其磁背景环境干净，干扰较小。

2 姿态测量与数据融合方法

本文中以发射点惯性系l 系为导航坐标系，建立捷联惯导（Strapdown Interial Navigation System，SINS）/地磁组合导航系统的状态方程和量测方程。

2.1 组合导航系统状态方程

2.1.1 数学平台失准角误差方程

忽略陀螺仪的一次项和二次项误差，数学平台失准角误差方程为

式中φ为数学平台失准角；Cbl为载体坐标系b 系到l系的变换矩阵；ε 为陀螺仪常值漂移；Wε为陀螺仪模型高斯白噪声。

2.1.2 加速度误差方程

忽略加速度计一次项和二次项误差，加速度误差方程为

式中δa为加速度误差；[ a ×]为加速度计敏感的比力组成的反对称矩阵；∇为载体坐标系b 系下加速度计的等效偏置。

2.1.3 速度位置误差方程

在发射点惯性坐标系中，简化引力场模型为球形有心力场，目标速度位置误差方程为

式中 系数f14, f15, f16, f24, f25, f26, f34, f35, f36为引力加速度对位置坐标的偏导数。

2.1.4 状态方程

综合数学平台失准角、加速度误差、速度误差和位置误差方程，可得如下系统状态方程：

式中X(t) 为状态向量，各分量分别为3 个数学平台失准角、速度误差、位置误差、陀螺常值漂移和加速度计常值偏置；F(t) 为状态转移矩阵。

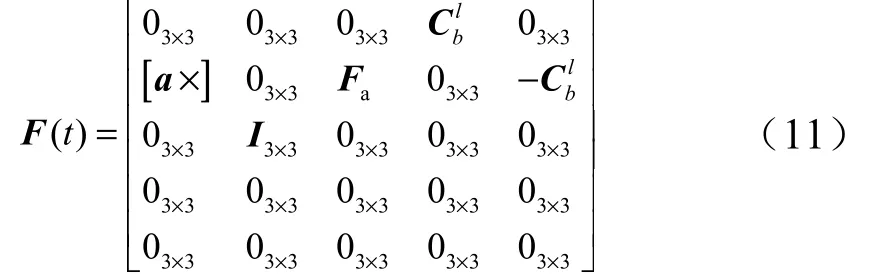
式中Fa为由式（12）元素组成的矩阵：

系统噪声驱动阵 G(t) 为

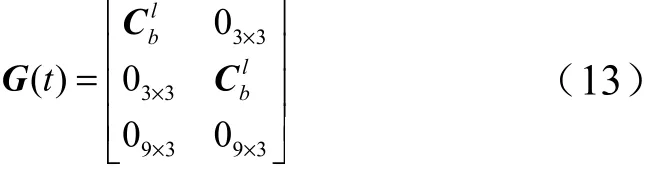
系统噪声 W(t) 为

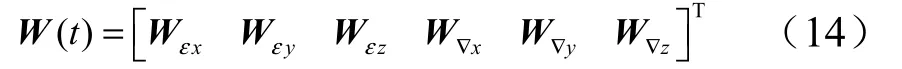
式中Wεx,Wεy,Wεz分别为陀螺误差；W∇x,W∇y,W∇z分别为加速度计误差。两者均为零均值的高斯白噪声误差。

2.2 组合导航系统量测方程

2.2.1 姿态误差角与平台失准角的关系

在捷联惯导系统中，载体姿态角是通过姿态矩阵（数学平台）计算出来的。理想情况下，导航计算机计算的导航坐标系（ lˆ 系）应和理想的导航坐标系（l 系）一致，然而，由于系统存在测量误差、计算误差和干扰误差等情况，计算的导航系与理想的导航系之间将产生偏差，对应的误差角为平台失准角，用角矢量表示。忽略二阶小量，l 系与lˆ 系之间满足如下关系：

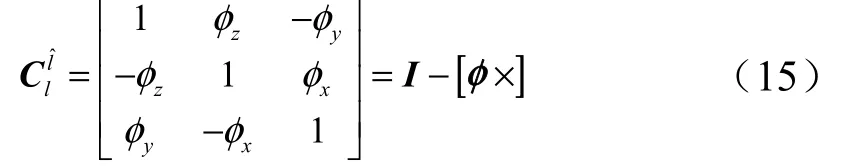
式中[φ × ]为平台失准角 φ的元素组成的反对称矩阵。

定义姿态误差角矢量η 为

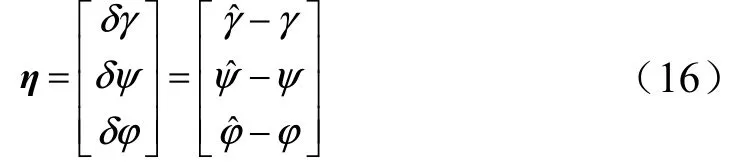
由姿态误差角的定义可知：

真实的姿态矩阵Clb可表示为

式中Clˆb为捷联解算的姿态矩阵。将式（10）和式（12）代入式（18），忽略二阶小量，可得l 系下姿态误差角与平台失准角关系：

式中M 为误差角转换矩阵：

2.2.2 观测模型

三轴磁强计测量值mB 可表示为

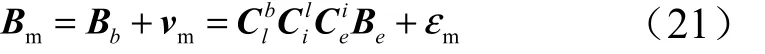
式中Be， Bb分别为真实的地磁场矢量在地球坐标系e 系和本体系b 系中的表示，Bb=ClbCilC eiBe；Cil为地心惯性系i 系到l 系的转移矩阵；Cei为e 系到i 系的转移矩阵； εm为量测噪声。

磁强计在载体预估状态下根据地磁场模型计算的地磁场强度值Bc可表示为

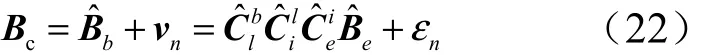
定义上述磁强计测量值Bm与根据地磁场模型计算的地磁场强度值Bc之差为量测 ∆ B：

令：

式中Ηl为磁强计的测量误差对l 系下载体位置的偏导数； xl为载体在l 系下的位置误差。

因此，最终的量测方程为

式中 Η 为量测矩阵，且：

2.3 基于反馈校正的卡尔曼滤波

卡尔曼滤波是一种线性最小方差估计。对卡尔曼滤波器估计的利用主要有输出校正和反馈校正，反馈校正性能优于输出校正。图1 为捷联惯性/地磁组合导航系统反馈校正解算框图。

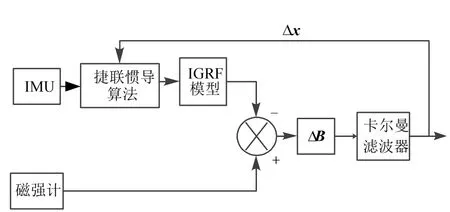
图1 捷联惯性/地磁组合导航系统解算框图 Fig. 1 The Strapdown Inertial and Geomagnetic Integrated Navigation System Feedback Correction Forward Solution Algorithm Diagram

使用卡尔曼滤波器时，若采用误差作为状态信息，引入状态反馈的目标是使输出信息尽可能趋于零。因此，滤波器估计值是校正后的导航参数差，即状态向量中包含的不再是陀螺常值漂移和加速度计常值偏置，而是陀螺常值漂移估计误差和加速度计常值漂移估计误差。反馈校正的滤波方程与标准卡尔曼滤波方程有所不同，详见文献[10]。

3 仿真与验证

3.1 仿真条件

a）飞行器发射点设定为：北纬40°，东经40°，发射方位角40°，初始偏航角0°，俯仰角90°，滚转角0°。

b）飞行器主动段飞行时间设定为200 s，发动机推力加速度设定为40 m/s2，方向沿飞行器体轴，其中，0～10 s 为垂直上升段，10～30 s 为主动转弯段，俯仰角从90°变为20°，30～200 s 为加速飞行段，俯仰角保持20°不变。

c）主动段仿真仅为提供本文的仿真初始参数，因此暂忽略其他因素影响。

d）仿真时间200～1728 s，为飞行器在轨自由飞行段，仅考虑飞行器重力影响。

在惯性/地磁组合中，捷联惯导的初始时刻姿态失准角分别为10″、6′和10″，磁强计工作开始时间为10 s。根据采样周期、惯组器件和磁强计的参数变化，设计6 种情形的典型仿真实例，如表1 所示。

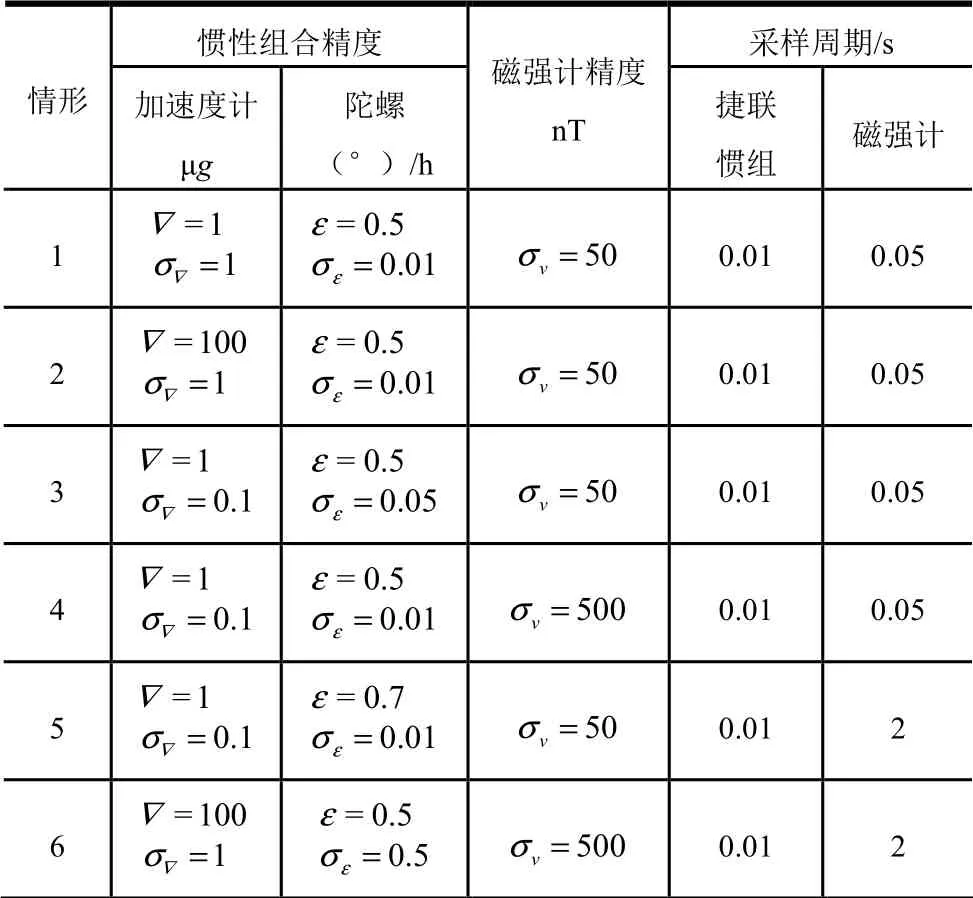
表1 仿真情形设计 Tab.1 Simulation Case Design

情形1：作为基准参照组，加速度计、陀螺仪、磁强计精度最高，采样周期时间最短。

情形2：降低加速度计的精度，通过滤波获得位置、速度和姿态误差结果。

情形3：降低陀螺仪的精度，通过滤波获得位置、速度和姿态误差结果。

情形4：降低磁强计的测量精度，通过滤波获得位置、速度和姿态误差结果。

情形5：增加磁强计的采样周期，通过滤波获得位置、速度和姿态误差结果。

情形6：同时降低加速度计、陀螺仪、磁强计精度，并增加磁强计的采样周期，通过滤波获得位置、速度和姿态误差结果。

3.2 仿真结果及分析

对情形1 至情形6 的位置、速度和3 个姿态角误差仿真结果进行统计分析，结果列于表2。

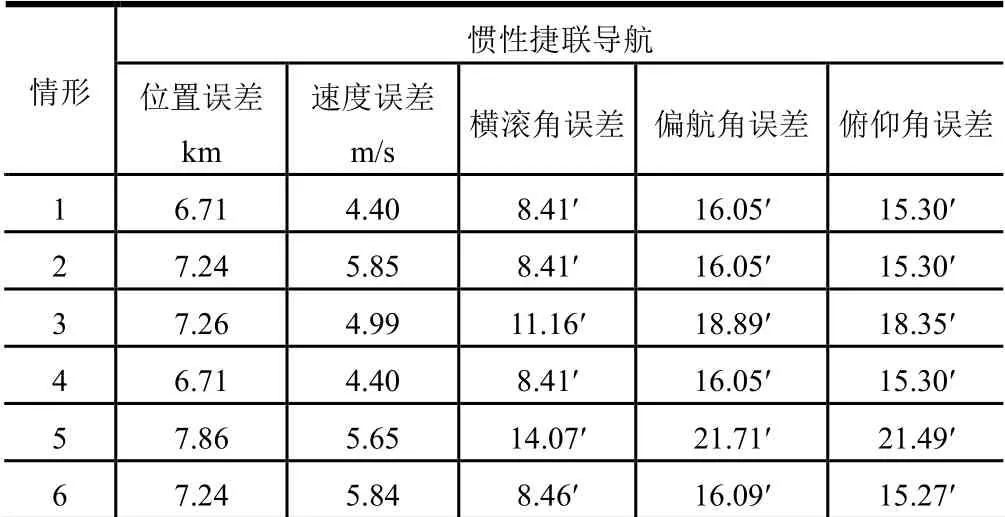
表2 仿真结果统计表 Tab.2 Statistics of Simulation Results

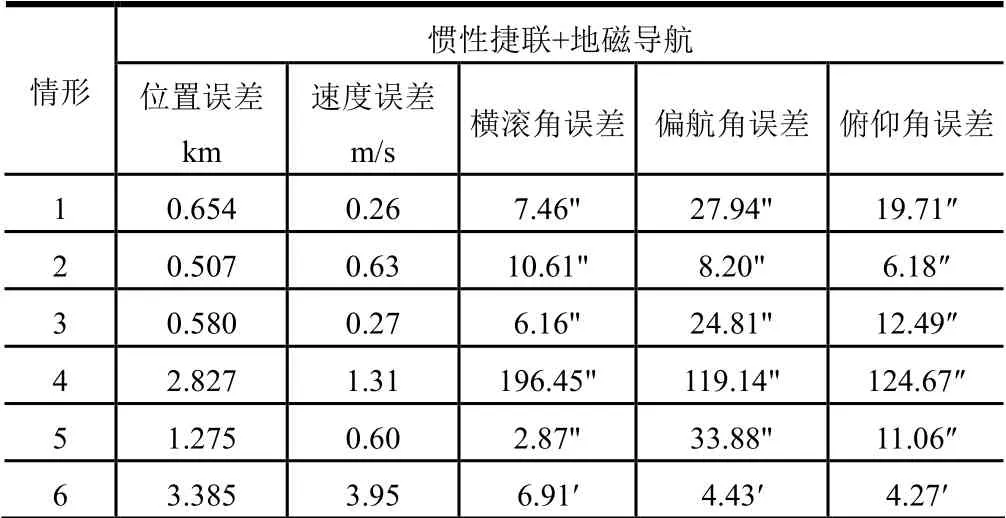
续表2

典型误差曲线如图2～6 所示。

图2 位置误差对比 Fig.2 Comparison of Position Error

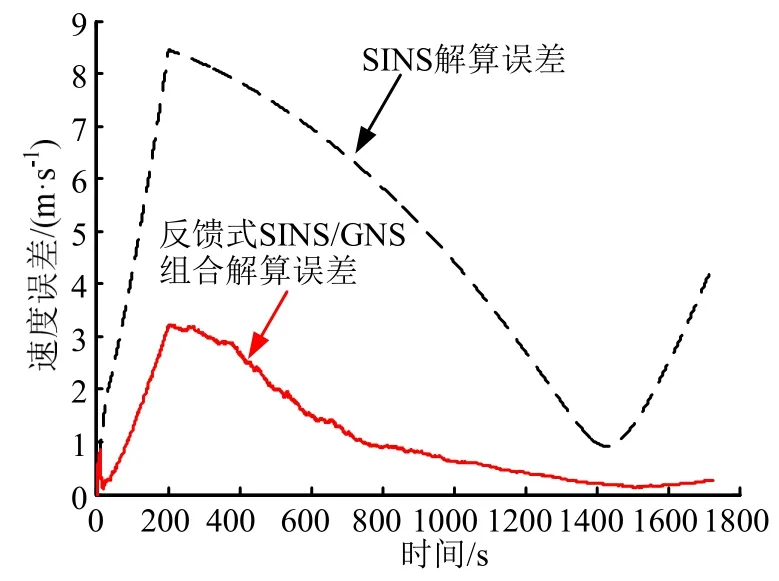
图3 速度误差对比 Fig.3 Comparison of Velocity Error

图4 横滚角误差对比 Fig.4 Comparison of Roll Angle Error

图5 航向角误差对比 Fig.5 Comparison of Yaw Angle Error

图6 俯仰角误差对比 Fig.6 Comparison of Pitch Angle Error

通过分析仿真结果，可得：

a）当仅仅依靠捷联惯导时，因加速度计常值偏置与陀螺仪常值漂移的影响导致位置姿态误差的发散。即便采用高精度加速度计和零漂稳定性达0.01（°）/h的陀螺仪，经过0.5 h 的飞行，因漂移而造成的位置、速度及姿态角的误差量级很大，如果没有其它导航方式的辅助融合，单独的捷联惯导应用于空间目标导航不可行。

b）情形2、3 与情形1 对照分析表明，当磁强计精度和采样率均较高时，惯性组合的精度降低，对捷联惯导/地磁组合导航精度影响不显著。

c）情形4、5 与情形1 对照分析表明，磁场强度的测量精度和采样率，均对捷联惯导/地磁组合导航系统精度具有影响，其中磁场强度的测量精度对其影响更显著。

d）情形6 与情形1 对照分析表明，当磁强计精度和采样率均较低时，惯性组合的精度降低，对捷联惯导/地磁组合导航精度影响显著。

4 结 论

捷联惯组与地磁进行组合导航，通过提高地磁测量的精度和采样率，在保持同等导航精度条件下，可显著降低对捷联惯组的精度要求；利用高精度MEMS磁强计可满足导航精度需求，降低轨道飞行器导航的经济、质量成本，减少安装空间。