平板锥形金属膜盒内压柱失稳理论研究

王亚军，陈牧野，周浩洋

（1. 中国航天科技集团有限公司，北京，100084；2. 北京宇航系统工程研究所，北京，100076）

0 引 言

目前中国运载火箭采用金属膜盒式蓄压器抑制“POGO”振动，其原理是通过金属膜盒的柔性来吸收输送管路中的压力脉动。金属膜盒一般采用内充压式结构，如图1 所示。

该形式膜盒存在内压柱失稳问题，一旦发生柱失稳，将会影响膜盒的工作性能和使用寿命，膜盒的柱失稳形态如图2 所示。

图1 内充压式膜盒示意 Fig.1 Metal Bellows Filling with Gas Inside

图2 膜盒柱失稳形态 Fig.2 Column Buckling of Metal Bellows

蓄压器用金属膜盒通常采用平板锥型结构。焊接膜盒有时也被称为焊接波纹管。在U 型波纹管的稳定性研究方面，国内外学者已经进行了比较全面的研究。J.A.Haringx[1]首先提出了“等效柱”的思想方法，该方法用于求解波纹管的柱失稳临界压力。朱卫平[2]在其文章中，证明了这种等效方法对于几种典型的支撑边界条件均成立。1988 年，Tsukimori[2]等人提出了波纹管受内压失稳的一种简化计算方法，对波纹管的弹性柱状失稳，平面失稳分别进行了理论分析，给出了对应的简化公式，并在此基础之上，通过利用弹-塑性轴向刚度代替弹性轴向刚度的方法，推导出简化的弹-塑性柱状失稳压力。1989 年，Broyles[4]对前人的研究成果进行总结，对波纹管的稳定性分析做了总结并进行了试验分析提出了相应的工程计算公式，该公式被美国膨胀节制造商协会所采纳。1995 年，郭学迅[6]验证了波纹管的抗弯刚度公式，并以此为基础来解答波纹管的柱状失稳和横向变形问题。2002 年，朱卫平[7]讨论了波纹管在内压作用下的柱失稳问题。在焊接波纹管研究中，樊大均[8,9]针对焊接波纹管进行了一系列的理论分析，由A.И.Лypьe 的锥壳方程出发，推导出了设计锥形焊接波纹管的可用理论结果，诸如该类焊接波纹管的变形、应力和有效面积的公式，为设计提供理论依据。在碟形波纹管研究方面，刘岩等[10]等根据EJMA 标准中U 形波纹管临界失稳内压的计算方法，得到了碟形波纹管平面失稳和柱失稳临界失稳内压的工程计算公式。

为获得工程适用的平板锥型金属膜盒柱失稳公式，本文基于由“等效柱”思想和欧拉公式得到的膜盒柱失稳公式，考虑到膜盒拉伸、压缩刚度不一致对“等效柱”抗弯刚度的影响，推导了拉伸、压缩模量不一致的薄壁圆筒抗弯刚度计算式，并推导得出适用于平板锥形金属膜盒的内压柱失稳公式。

1 平板锥型金属膜盒的柱失稳分析

由于柱失稳的公式是通过两端固支的压杆稳定性公式推导，其中波形对柱稳定性的影响主要体现在对单波轴向刚度的影响上[10]，而平板锥形膜盒与其它波纹管仅存在波形上的差异，因此分析平板锥形膜盒柱失稳与分析波纹管柱失稳思路相同，将膜盒等效为受内压的薄壁圆筒，再将受内压的薄壁圆筒等效为受轴向力的薄壁圆筒，从而得出膜盒的柱失稳临界压力。等效过程如图3 所示。

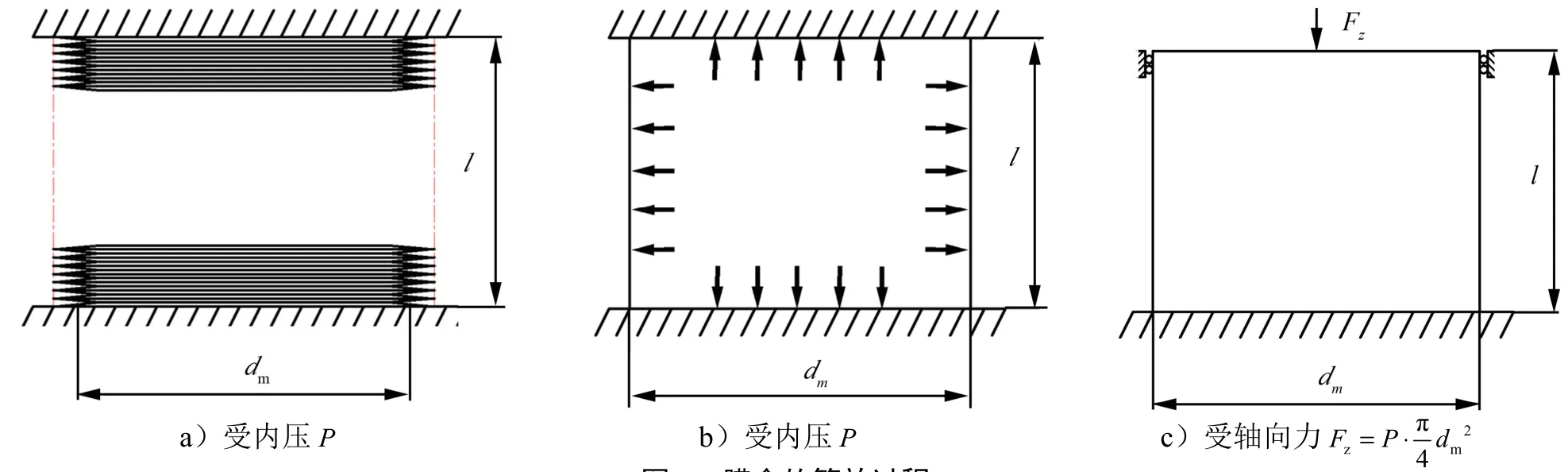
图3 膜盒的等效过程 Fig.3 Equivalent Process of Metal Bellows

根据欧拉失稳公式即可以给出膜盒的内压柱失稳公式[6]：

式中 W 为膜盒的抗弯刚度；md 为膜盒的中径；l 为膜盒的高度；µ为长度系数，反映不同支承影响的系数。本文为两端固定的情况，µ取0.5。

对于一般结构的膜盒，当其轴向拉伸和压缩刚度一致时，抗弯刚度可以用单波轴向刚度来表示，有其中，if 为膜盒的单波轴向刚度，式（1）可以写成[6]：

式中N 为膜盒的波数；q 为膜盒的波距，有l Nq= 。

2 平板锥形金属膜盒的刚度分析

对于蓄压器用平板锥形金属膜盒，其膜片的结构示意图如图4 所示。由图4 可知，膜盒的波距为2q h= ，膜盒的膜片数为2n N=，膜盒的中径

膜片通过直边段焊接相连，但只是对部分直边段进行了焊接。因此膜盒压缩与拉伸时相比，未焊接的直边段由于接触产生相互作用，使得膜盒的刚度变大。所以蓄压器金属膜盒的拉伸和压缩轴向刚度并不一致，因此在研究蓄压器金属膜盒时，需要考虑膜盒拉伸、压缩轴向刚度不一致的问题。

图4 平板锥形膜盒结构示意 Fig.4 Plane-cone Shaped Metal Bellows

焊接膜盒的轴向整体拉伸刚度经验公式[12]为

式中mE 为材料的弹性模量。

当膜盒处于压缩状态时，膜盒的直边段实际处于贴合状态，相当于膜盒的内径、外径发生了变化，因此式（3）不能直接计算膜盒压缩刚度，需要对相关参数进行修正。设压缩状态下的等效外径、内径、波高、直边段长度分别为 'D 、 'd 、 'w 、'L直边，L直边为膜片实际的直边段长度，有则由等效直边段长度即可求得膜盒压缩刚度。

下面采用理论公式计算和ABAQUS 仿真相结合的办法确定等效直边段长度。有限元仿真采用轴对称模型，通过获取轴向力与轴向位移的方法求解出刚度。取5 种规格不同的平板锥形金属膜盒，各膜盒具体的尺寸参数及柱失稳试验值见表1，材料参数见表2。

表1 各膜盒尺寸参数及柱失稳试验值 Tab.1 Dimension Parameters and Experiment Buckling Pressure of Each Metal Bellow

表2 各膜盒材料性能参数 Tab.2 Mechanical Property Of Each Metal Bellows

为了验证有限元计算刚度的可靠性，以5 号膜盒为对象，进行轴向拉、压刚度试验，得到5 号膜盒的拉伸刚度为19 N/mm，压缩刚度为23 N/mm。使用有限元得到的拉伸刚度为19.35 N/mm，压缩刚度为 23.71 N/mm。对比可知可以使用有限元方法仿真膜盒的轴向拉伸压缩刚度。由于式（3）本身的计算值与仿真值存在一定偏差，因此将拉伸刚度和压缩刚度的比值作为计算值与仿真值比较的依据。通过对不同等效直边段长度的计算表明，当等效直边段长度取时，与有限元结果吻合较好，计算结果见表3。因此，在将直边段长度等效为后，可以使用式（3）来求解膜盒的压缩机械刚度。

表3 各膜盒拉伸、压缩刚度比值的计算和仿真结果对比 Tab.3 Calculation Result of Stiffness Compared to Finite Element Method

从轴向刚度计算式中可以看出，该计算式并未考虑充内压后膜片受压变形等因素对轴向刚度可能带来的影响，因此在使用式（3）计算膜盒轴向刚度进而求解膜盒的内压柱失稳临界压力时，膜盒应该满足在充压后保持刚度基本不变的条件。当出现下列情况时，认为膜盒的刚度在充压过程中不符合轴向刚度基本不变的条件：a）充压后膜片与膜片焊缝附近应力集中区进入穿透性塑性；b）充压后膜片与膜片的中部在内压下发生贴合。

3 膜盒柱失稳公式

由于平板锥形金属膜盒的压缩和拉伸轴向刚度不一致，故直接使用式（3）结果代入式（2）求解得到的内压柱失稳压力值可能不准确。因此考虑使用式（1）求解膜盒的内压柱失稳临界压力。式（1）中，受膜盒的压缩和拉伸轴向刚度不一致影响的变量仅为抗弯刚度W 。在第1 节中将膜盒等效为薄壁圆筒，该过程实际上是将膜盒的抗弯刚度与薄壁圆筒的抗弯刚度进行了等效，求解薄壁圆筒的抗弯刚度即可知膜盒的抗弯刚度。

图5 为薄壁圆筒的弯曲示意。如图5 所示，薄壁圆筒的外半径为R，内半径为r，壁厚为t。1y 为横截面最顶部与y 轴交点的坐标，其大小为横截面最顶部距中性层的距离。为求解薄壁圆筒的抗弯刚度，令薄壁圆筒只承受x y− 平面内的弯矩。

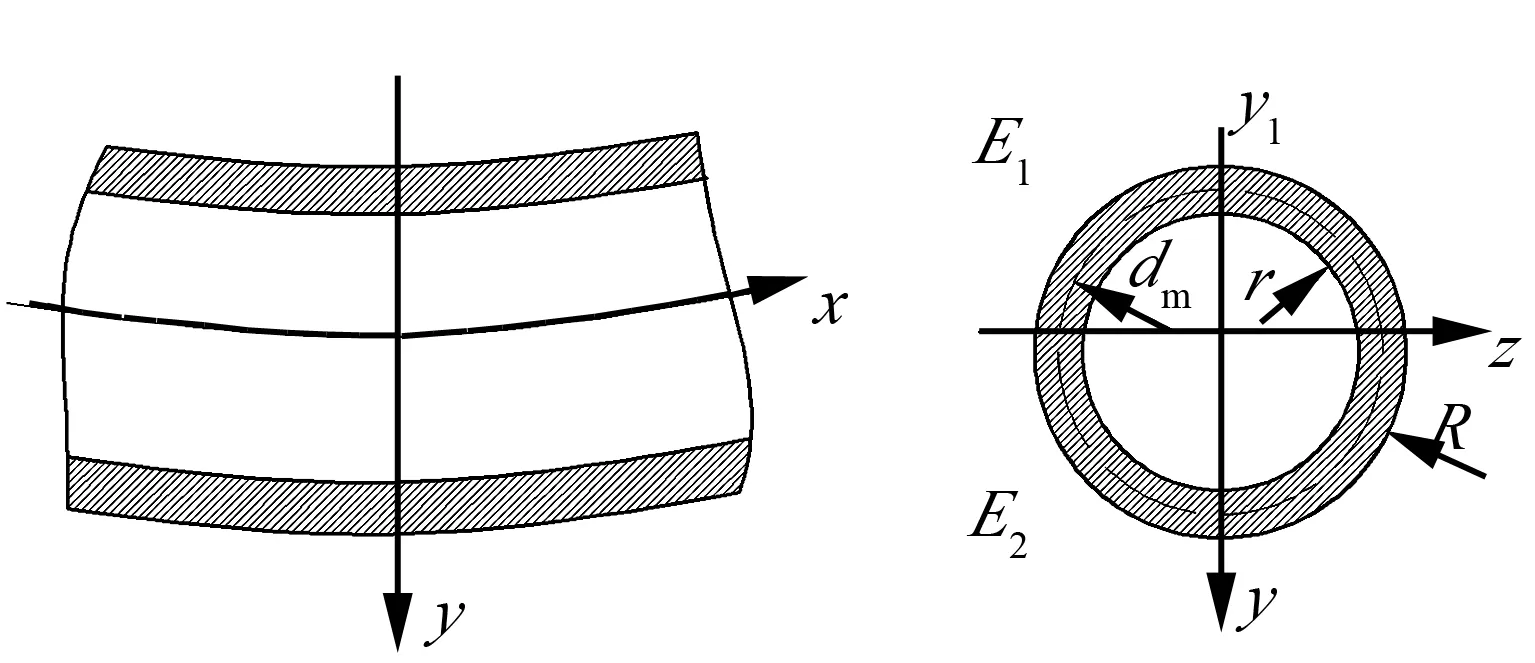
图5 薄壁圆筒的弯曲示意 Fig.5 Bending Diagram of Thin-alled Cylinder

式中σ 为正应力；E 为薄壁圆筒的弹性模量；y 为距离中性层的距离；ρ 为中性层的曲率半径。

横截面上各点处的法向微内力 σ dA组成一空间平行力系，而且，由于横截面上没有轴力，仅存在于位于xy 平面的弯矩Mz，因此，内力 FN以及弯矩Mz为

由图5 可知，中性层以上部分受压，中性层以下部分受拉。设横截面中性层以上部分面积为 A1，中性层以下部分面积为 A2。则内力 FN以及弯矩Mz为

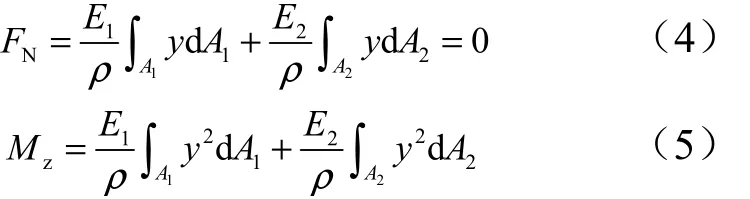
则薄壁圆筒的抗弯刚度为

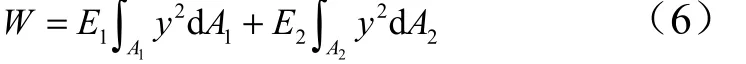
联立式（4）和式（6），即可得出拉伸、压缩弹性模量不一致的薄壁圆筒的抗弯刚度W 。将式（6）的结果代入到式（1）中，即可以得到拉伸、压缩机械刚度不一致的金属膜盒的柱失稳临界失稳压力值。

为简化计算，令 E1=aE2， y1= bR，r = cR。对内力FN和抗弯刚度W 分别进行积分，并写成由 E2、R、a、b、c 表示的式子，则由式（4）和式（6）可得：

由上文的分析可知，压缩模量大于拉伸模量，即E1> E2，同时平板锥形金属膜盒结构一般满足R > r>0.5R 。在上述给定范围内，E1、r 分别取均布的100 个点，共100×100 个点，采用数值拟合的方法，联立式（1）、式（7）和式（8）可得：

4 计算结果分析

使用第2节计算得到的各膜盒刚度数值代入式（9）中，即可求得各膜盒的柱失稳临界压力计算值，结果如表4 所示。表4 中同时对比了不考虑拉伸、压缩轴向刚度不一致，以式（3）刚度值代入式（2）得到的失稳值与式（9）得到的失稳值的误差。对比考虑了拉伸、压缩轴向刚度不同的柱失稳计算结果与直接使用刚度经验式（3）求解得到的柱失稳计算结果，考虑了拉伸、压缩刚度不一致得到的柱失稳计算结果的精度总体要更优。

表4 各膜盒失稳公式计算值与试验值比较 Tab.4 Comparision between Different Formula Calculation Results and Expriment Results

观察式（9）计算结果，通过对比，膜盒1～4，其失稳值与试验值的误差范围在-30%～25%以内。而膜盒5 的误差则达到93.3%。建立膜盒的轴对称模型，将膜盒固定至限位高度，给膜盒内部施加压力至柱失稳计算压力值，提取各膜盒的等效塑性应变（Equivalent Plastic Strain，PEEQ）云图，观察膜盒膜片焊接应力集中区应变情况以及膜片中部接触情况，结果见图6。

图6 各膜盒膜片中部接触情况和应力集中区应变情况 Fig.6 Equivalent Plastic Strain and the Collide Condition

从图6 中可见，在失稳计算值压力下，膜盒1～4膜片中部均未发生接触，且焊接应力集中区域未进入穿透性屈服；观察图6e，5 号膜盒的膜片由于受内压鼓胀，中部部分发生了接触。同时在焊缝处，等效塑性应变值均大于零，可知膜盒在焊接区域进入了穿透性屈服。膜盒膜片中部接触或焊接区域进入穿透性屈服后，膜盒的轴向刚度将会发生变化，故5 号膜盒的轴向刚度在充压后不满足基本不变的假设。因此膜盒5采用公式计算的失稳值结果误差较大。

目前采用式（9）计算的膜盒失稳压力值与试验值存在±30%左右的偏差，主要是由以下原因所致：

a）膜片的实际几何形状（如壁厚，内外径等尺寸）与理论存在偏差；

b）柱失稳试验采用目视估读的方法获取失稳值，该方法存在一定的随机误差；

c）采用的刚度计算公式存在一定的误差。

5 结束语

本文对平板锥形金属膜盒在拉伸和压缩两种情况下轴向刚度的不一致情况进行了分析，基于由“等效柱”思想和欧拉公式得到的膜盒柱失稳公式，推导了拉伸、压缩轴向刚度不一致下的膜盒抗弯刚度，并获得了该类膜盒的内压柱失稳公式。计算结果与试验结果的比对表明该公式有效，可用于求解满足刚度基本不变假设的平板锥形膜盒的柱失稳临界值。