再生冷却氢氧推力室传热计算方法研究与优化

巩岩博，刘忠恕，郑大勇，王维彬

（北京航天动力研究所，北京，100076）

0 引 言

推力室是火箭发动机的核心部件之一，担负着将推进剂的化学能转化为热能，并将热能转化为机械能的功能。在推力室工作时，有限空间内的剧烈燃烧会产生非常高的压力和温度，巨大的热流会将内壁加热到很高的温度，同时在室壁中产生很大的温度梯度，极易造成推力室结构破坏。为了保证结构安全、延长推力室寿命，必须对室壁进行冷却。大推力液体火箭发动机广泛采用再生冷却法。

在设计再生冷却推力室时，需要进行传热分析与计算，以确定内壁温、冷却剂温升、冷却剂压降等关键参数。一般可以通过试验、计算和数值模拟等手段进行[1]。在工程中，因计算简单、使用方便，常常使用一维试验关联式进行计算[2]。试验关联式是一种半经验公式，难以考虑所有的影响因素，在针对不同的计算对象时，并不能很准确地反映计算对象的实际情况[3]。尤其是燃气侧传热，由于燃气的物性与推进剂相关，且燃烧与流动过程非常复杂，在针对氢氧发动机时，通过最常用的巴兹法[3]得到的结果，与试验结果并不能很好地吻合。

为了更好地分析与计算氢氧火箭发动机的再生冷却过程，本文通过分析推力室中的燃烧与流动过程，并结合氢氧推力室传热试验，对再生冷却的计算方法进行修正，形成更加适应氢氧火箭发动机的再生冷却计算方法。使用该方法与传统的再生冷却计算法分别开展计算，并将计算结果与某型号氢氧火箭发动机的试车试验结果进行对比，表明改进后的传热计算方法的准确性和适应性更好。

1 再生冷却传热模型与改进

再生冷却推力室的结构包括内壁、外壁和冷却通道，如图1 所示。

图1 再生冷却传热模型 Fig.1 Model of Regeneratively-cooled Heat Transfer

因结构复杂，其传热过程也相当复杂，主要包括：a）高温燃气向推力室内壁的对流传热；b）高温燃气向推力室内壁的辐射换热；c）推力室内壁中的热传导；d）推力室内壁向冷却剂的对流传热；e）冷却剂向推力室外壁的冷却传热；f）推力室外壁中的热传导； g）推力室外壁向大气的对流传热；h）推力室外壁向大气的辐射换热。在发动机稳定工作时，与燃气向推力室内壁传热的热流密度相比，推力室外壁与大气之间的传热量非常小，忽略掉冷却剂向推力室外壁及外壁向大气的传热，对计算结果的准确性几乎没有影响。因此，在进行再生冷却换热时，只需要考虑高温燃气向推力室内壁的对流传热和辐射换热、推力室内壁中的热传导和推力室内壁向冷却剂的对流传热，并假设推力室内壁的热传导只沿径向进行。

1.1 燃气向内壁传热

燃气向推力室内壁的传热由对流传热和辐射传热两部分构成。

1.1.1 对流传热

高温燃气向推力室内壁的传热属于强迫对流传热。燃气的高速流动会在内壁面形成湍流边界层，而湍流边界层在紧贴壁面处存在一个层流底层，因此燃气与内壁的对流换热过程实际上是由燃气向层流底层的对流换热和层流底层内的热传导组成的[1]。由于附面层及其换热过程的计算复杂，因此采用如下基本关系式进行计算[3]：

式中 qg为燃气侧热流密度， W/m2； hg为对流传热系数， W/(m2⋅ K)； Taw为绝热壁温，K； Twg为燃气侧内壁温度，K。

由于燃气的组分、性质、燃烧和流动非常复杂，再加上边界层的影响，无法通过理论计算的方式得到对流换热系数，因此一般使用半经验公式进行计算。最常使用的是巴兹公式，即：

式中 σ 为定性温度变换系数，用下式计算：

式中 Dt为喉部直径，m；µ为燃气滞止温度下的动力粘度，Pa ⋅ s； cp为燃气滞止温度下的定压比热，J/(kg ⋅ K)；Pr 为燃气滞止温度下的普朗特数； ( pc)ns为推力室室压，Pa；c∗为推力室特征速度，m/s；σ 为定性温度变化系数；R 为喉部曲率半径，m；At，A 分别为喉部面积和分段处截面积，m2；Tc为推力室温度，K；γ 为燃气比热比。

式（2）考虑了沿附面层横向气流物性参数的变化和推力室几何形状等因素对传热过程的影响[1]，但并未考虑推力室入口附近推进剂雾化蒸发区的影响，不能真实地反映沿发动机轴向的热流分布；也未考虑近壁面气体雷诺数对传热的影响[2]，导致计算出的结果与试验数据相比有一定的偏差。

由此可知，通过理论分析和传热试验，对传热计算模型进行修正。由于推力室不同区域的流动与传热有着不同的特点，因此分段进行修正。

1.1.2 靠近头部的区域

对于双组元液体推进剂，进入推力室后要经历雾化、蒸发、混合和燃烧才能转化为燃气，这需要一定的时间和距离。在紧靠喷注面板的一段区域内，主要进行推进剂的雾化和蒸发，叫做雾化蒸发区[4]。该区域内尚未发生燃烧，主要成分是低温推进剂，由于推进剂喷注速度很大，液体与气体的摩擦力会带动液流周围的气体向前流动，形成一个局部低压区，使得高温高压的燃气回流，但大量的热量会被推进剂蒸发过程所吸收，因此该区域内的温度要远低于燃气温度。经验表明，对于氢氧火箭发动机，该区域轴向长度约为10～40 mm，在与之相邻的区域内，已经蒸发完成的推进剂相互掺混、组织燃烧，即掺混与燃烧区。在该区域内，推进剂边掺混边燃烧，温度逐渐升高，化学反应速度也随温度的升高而增加，并达到最大值。在该区域内，温度可视为近似等于最大燃气温度，但由于掺混不均匀、燃烧不完全，因此对流传热系数要低于主流燃气，并随轴向的增加而增大[5]。

对特定的推力室而言，其雾化蒸发区轴向长度 xv与掺混燃烧区轴向长度 xm是一定的。根据工程经验，对于采用气液喷注器的大推力火箭发动机， xv与 xm可分别选取为推力室轴向总长度的1/50 和1/25。轴向长度x 在 0 ≤ x ≤ xv范围内，根据部件传热试验结果对主流温度进行修正：

式中 Tc′为修正后的雾化蒸发区总温； Tc为推力室主流的总温。

轴向长度x 在 xv≤ x ≤ xm范围内，根据下式修正传热系数[6]：

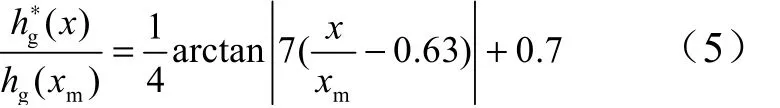
1.1.3 主流区域

在主流区域，燃气惯性力与粘性力的相对关系，即燃气雷诺数的大小对巴兹公式的准确性有较大的影响。当雷诺数较大时，燃气的惯性力占主导地位，粘性力的影响减小，传热随之增强。文献[7]通过与试验对比，发现在大雷诺数条件下，忽略粘性力影响的Cinjarew 公式比巴兹公式有更高的准确性[7]。因此，在计算中考虑燃气雷诺数大小的影响，可以得到更准确的结果。由分析可知，燃气雷诺数的大小受推力室压力、混合比及几何参数的影响，结合氢氧推力室传热试验结果，引入修正系数reC ，如下式：

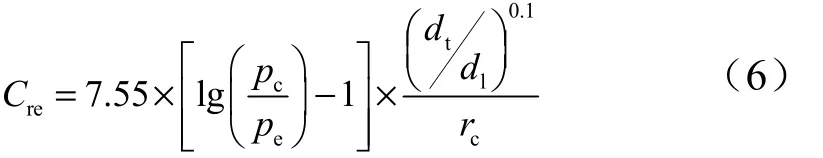
式中ep 为大气压强；cr 为推力室混合比；td 为推力室喉部直径；ld 为圆筒段直径。所有参数均采用国际制基本单位。则修正后的燃气侧燃热系数为

在巴兹公式中，普朗特数Pr 使用以下简化关系式进行近似计算[8]：

式中 κ 为燃气比热比。通过与氢氧燃气传热试验对比，发现传统关系式计算出的 Pr 值与实际值存在13%～18%的偏差。由计算得知，对流换热系数对Pr 值较为敏感，因此将传统关系式修正为

1.1.4 辐射换热

氢氧火箭发动机推力室中的燃气不含固体微粒，能产生辐射的主要成分是 H2O 气体，辐射热流密度（以qr表示）取决于燃气温度和压力、 H2O 的分压以及燃烧室的几何尺寸[1,8]。与对流换热相比，辐射换热的量级小得多[8]，计算误差对最终结果影响不大，因此常根据经验进行简化计算。

1.2 通过内壁的传热

在内壁中，热能是通过热传导的方式进行传递的，根据傅里叶导热定律[9]，通过内壁的热流为

式中wq 为内壁导热热流密度，2W/m ；wλ 为内壁导热系数，W/(m K)⋅ ；wδ 为壁面厚度，m；wlT 为内壁冷却剂侧内壁温度，K。

可以看出，在温差一定的条件下，内壁的导热能力与导热系数成正比，与内壁的厚度成反比。其中，导热系数的大小与材料的种类和定性温度的高低有关，在计算中，定性温度取内壁两侧壁温的平均值，根据材料导热系数与温度的关系制作插值表，通过插值表确定导热系数。

1.3 内壁向冷却剂的传热

内壁向冷却剂的传热是内部强迫对流传热。根据牛顿冷却公式[9]，由内壁传递给冷却剂的热流为

式中 ql为冷却剂侧热流密度， W/m2； hl为冷却剂对流传热系数， W/(m2⋅ K)； Tl为冷却剂温度，K。

对于氢氧火箭发动机，一般使用液氢作为冷却剂，当发动机处于主级工作状态时，液氢为超临界状态，因此使用液氢在超临界状态下的试验关联式计算对流系数[10]：

式中wν 的定性温度wT 为壁面温度；bν 的定性温度bT为冷却剂中心区温度，单位均为K。

为了增强换热能力，大推力液体火箭发动机的推力室内壁多使用带有肋条的铣槽式结构，肋条可以大大增加换热总表面积，减小换热热阻，从而使传热量增大。因此，计算时必须考虑肋对换热的影响，在热流密度lq 的基础上乘上肋壁传热修正系数fη 。肋效率表示实际散热量与假设整个肋表面处于肋基温度下的散热量的比值，对于等截面直肋，肋效率为[9]

其中，

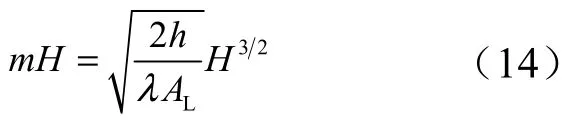
式中 h 为对流传热系数；λ 为肋片导热系数；δ 为肋片厚度；H 为肋高；LA 为肋片的纵截面积。

2 推力室换热计算模型

推力室型面分段如图2 所示。由图2 可知，推力室型面分段是典型的推力室身部剖面。根据几何形状和流动特点将其分为圆筒段、喷管收缩段、喉部区域和喷管扩张段4 个部分。由于推力室型面复杂，且燃气参数和冷却剂物性沿轴向变化很大，因此在计算时，将推力室沿轴向划分为若干小段，将每一段近似看做一个圆柱，且段内采用集中参数法，将每一段中点的参数作为该段的平均参数[11]。每一段的长度根据推力室内各参数沿轴向变化的剧烈程度确定，如喉部区域的热流密度和温度梯度最大，因此分段需要更密集。最终确定4 个部分分段的长度分别为10 mm、8 mm、6 mm 和8 mm。

图2 推力室型面分段 Fig.2 Segmentation of the Thrust Chamber Profile

将推力室内的燃气流动视为一维等熵绝热流动，使用气动函数计算出每个分段截面处的马赫数、温度和压力等参数值，然后从冷却剂出口截面开始，在每个分段内建立一维能量方程，即 qg+qr= qw= ql，并使用改进的再生冷却传热模型进行计算。边界条件为每个分段的冷却剂入口温度和压力等于上一个分段的冷却剂出口温度和压力。通过计算可以得到推力室内壁燃气侧温度和冷却剂侧温度分布、传热热流密度分布、冷却剂温升和压降等重要参数。

3 仿真计算与分析

分别使用传统的再生冷却传热模型和改进后的再生冷却传热模型对某型50吨级氢氧发动机推力室进行计算，并与试车试验数据进行对比，以验证改进的有效性。该氢氧火箭发动机推力室内壁材料为铜合金，铣槽式结构，考虑到不同部位的几何尺寸和换热需求，采用分段式设计，圆柱段和喷管收缩段冷却通道深宽比5.4，喉部区域深宽比6.4，喷管扩张段深宽比3.7。推力室室压10.2 MPa，混合比6.4，喷管收缩比2.6。

3.1 额定工况计算结果

分别使用两种计算模型对该型发动机在额定工况下的再生冷却传热进行计算，得到传热热流、燃气侧壁温、冷却剂温度沿轴线的分布，如图3～5 所示。

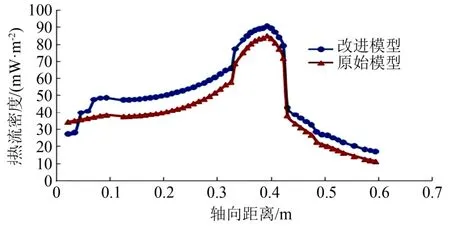
图3 热流密度轴向分布曲线 Fig.3 Distribution of Heat Flux Density Along the Axial Direction

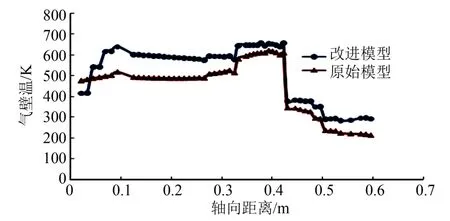
图4 气壁温轴向分布曲线 Fig.4 Distribution of Gas-sidewall Temperature Along the Axial Direction

从图3 可以看出，原始模型和改进模型计算出的热流密度在变化趋势上基本一致，圆筒段较为平稳，到喉部位置急剧升高，喷管扩张段又急剧下降并沿轴向逐渐降低，但是在非常靠近头部的位置，原始模型未能反映出真实发动机在此处热流较低的情况，而改进模型则考虑到了相关因素，计算出的热流密度在头部较低，逐渐升高到与圆筒段一致，更加接近实际情况。另外，原始模型计算出的热流整体低于改进模型的计算结果，这是由于改进模型考虑了燃气湍流度对传热过程的影响。由图4 可知，改进模型的计算结果在靠近头部的区域更加接近真实的物理过程，即在非常靠近头部的区域内，燃烧尚未发生，因此越接近头部主流温度越低、对流传热系数越小，进而气壁温就越低。由图5 可知，改进模型计算出的温升速度更大，通过与试验数据的对比，发现改进模型计算出的冷却剂出口温度与实际情况更加接近，表明改进模型更能准确地反映真实的传热过程，也间接说明在图3 和图4中，改进模型的计算结果更加可信。由此可见，与原始传热模型相比，改进模型有更高的准确性和可信度。

3.2 多工况验证

为进一步验证改进后传热模型的准确性和适应性，从该型发动机大量的试车参数中选取不同台次的低工况、额定工况和高工况状态进行计算，得到夹套温升与压降，并与试车试验数据对比，结果如表1～4 所示。

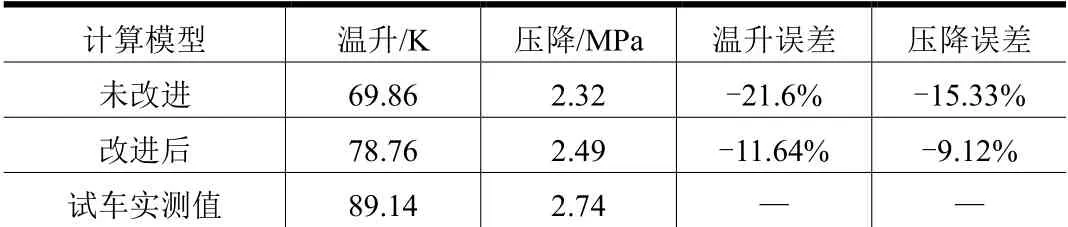
表1 低工况状态（ pc =9.937MPa， r =6.06） Tab.1 Condition of Low Load（ pc =9.937MPa ，r =6.06）

表4 高工况状态（ pc =10.391MPa ，r=6.791） Tab.4 Condition of High Load（ pc =10.391MPa ，r=6.791）

从表1～4 可以看出，在计算夹套温升时，未改进的计算模型存在较大的误差，3 个算例中均高于15%，而改进后的计算模型大幅度提高了计算精度，误差较之前减小了一半以上，证明基于燃烧和流动过程分析的改进是有效的；在计算压降时，未改进的模型已经具有较高的准确度，误差在10%上下，而改进后的模型计算精度大幅提高，低工况下误差下降近50%，额定工况和高工况下误差更是大幅减小。尽管低工况下的计算精度不如额定工况和高工况，但是误差已经减小到工程所能接受的范围。此外，通过对比可以看出，改进后的模型在不同工况下都具有较高的精度，且误差相对稳定，证明改进后的模型具有良好的适用性和稳定性。

综上，与原模型相比，改进后的计算模型在针对氢氧发动机时具有更高的准确性和更好的适用性，在准确预测冷却夹套的温升压降，以及指导发动机设计方面具有积极的意义。

4 结 论

本文针对传统再生冷却传热模型在计算氢氧火箭发动机时误差较大的问题，通过对物理过程的分析与试验数据的对比，对原模型进行相应的修正，提出改进的传热模型，并分别使用两种模型对某型氢氧火箭发动机推力室传热过程开展计算，将结果与试车试验结果进行对比，发现改进的再生冷却传热模型明显减小了计算误差，具有更高的准确度，并且在不同工况下均具有良好的适应性，表明改进后的再生冷却传热计算模型可以为氢氧火箭发动机再生冷却推力室的传热计算提供更加有效的帮助。