横摇与纵摇对小型船用反应堆堆芯入口处冷却剂流量特性影响研究

2022-03-10刘懿锐袁江涛祁杰张鑫

中国科技纵横 2022年1期

刘懿锐袁江涛祁杰张鑫

（1.中国人民解放军海军潜艇学院，山东青岛 266199；2.中国人民解放军92730部队，海南三亚 572000）

0.引言

舰船在水面航行，受到风浪等自然因素的影响会发生横摇与纵摇的现象[1]。横摇与纵摇会对反应堆堆芯入口冷却剂流量产生影响，而堆芯入口冷却剂流量关系到核动力装置的安全运行，是核安全分析的重要参数，所以研究横摇与纵摇条件下堆芯入口冷却剂流量变化和流量分布十分重要。

现阶段对于横摇与纵摇条件下小型船用反应堆研究还不完善，仅利用理论推导的方式从系统层面进行研究[2]，缺少对堆芯入口流量分布细节的计算。本文通过CFD软件STAR-CCM+建立反应堆全堆模型，分析横摇与纵摇对冷却剂流量的影响。

1.模型建立

1.1 几何模型

反应堆RPV的两进口接管、两出口接管之间夹角为120°，同侧进口接管、出口接管间夹角为60°。根据冷却剂流动建立计算域包括入口管段、下腔环腔、下腔室、下板孔、堆芯、上板孔、上腔室和出口管段。

1.2 网格划分

目前主要的网格划分技术有多面体网格、四面体网格与六面体网格。相比四面体网格与六面体网格，多面体网格在保证节点数量的同时具有最小的网格数量，且对复杂结构有较好的适应性。本文采用多面体网格的方式对计算域进行离散。考虑到堆芯入口为本文的重点研究内容，所以对堆芯入口处进行细网格划分如图1所示。

图1 堆芯入口处网格划分情况

1.3 边界条件设置

反应堆入口处设置为质量流量进口，并设置入口质量流量与温度。两出口设置为压力出口，压力设置为0，参考压力设置为工作压力。其余边界设置为壁面。堆芯处设置为多孔介质区域，根据堆芯压降与堆芯处冷却剂流速设置堆芯惯性阻力系数与粘性阻力系数[3]。选用标准湍流模型，2层全y+壁面函数。计算收敛至1×10-4。

1.4 网格敏感性分析

根据设置条件，进行网格敏感性分析，分别划分粗网格（290W）、中等网格（760W）、精细网格（893W）利用下腔室中心轴线处冷却剂流动速度作为指标，具体示意图如图2所示。

图2 冷却剂流速与网格关系图

从图2中可知，当网格数量达到760万后，下腔室中心位置流速随网格数量变化很小，综合考虑计算速度、精度，选择网格数量为760万进行后续计算。

1.5 摇摆模型

1.5.1 坐标系的建立

在研究系统摇摆的问题中需要建立新的坐标系，这样可以避免因惯性系发生变化带来研究对象内部流体与坐标系之间发生位移引起的流动特性捕捉困难的问题。在研究中我们建立的局部坐标系称为非惯性坐标系。建立非惯性坐标系的方法如图3所示。

图3（a）是我们最常用构件局部坐标系的情况，但是本文主要研究冷却剂在反应堆内的流动特性，冷却剂在反应堆内的主流方向为竖直向上，为了方便分析故选择图3（b）中非惯性坐标系的建立方式。

在海洋环境下舰船受到海浪与海洋内波的影响，在舰船系统中引入的摇摆扰动可分为横摇与纵摇。横摇是沿如图3（b）中非惯性坐标系x轴发生的左右摇摆运动，从艇首向艇尾看，向左倾斜为正；向右倾斜为负；纵摇是沿如图3（b）中非惯性坐标系y轴发生的摇摆运动，向前倾斜为正；向后倾斜为负。

图3 坐标系示意图

1.5.2 摇摆状态受力分析

摇摆运动可以简化为单一自由度的简谐运动，且研究为反应堆随船体横摇、纵摇内部流场发生的变化，则系统摇摆角度变化、角速度、角加速度[4]可写为：

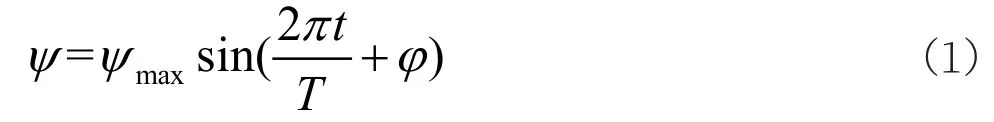
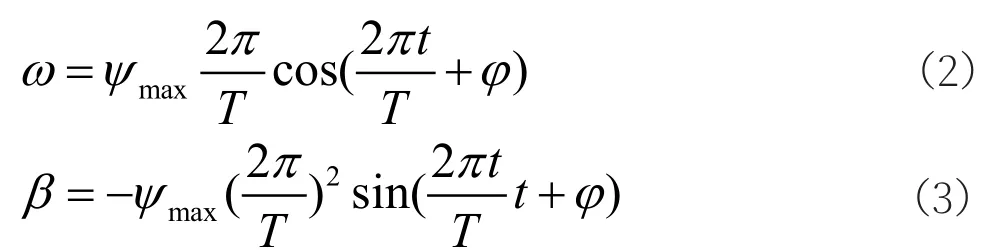
式中，ψ为摇摆角度；T为摇摆周期；φ为摇摆初始相位；ω为角速度；β为角加速度。

则系统因摇摆条件所受外力可写为：

式中，Fr为系统因摇摆所受外力；为重力；为切向力；为离心力；为柯氏力。

引入摇摆运动后系统受力示意图如图4所示。

图4 系统受力

2.数值模型的验证

2.1 稳态模型的验证

经稳态计算，堆芯入口归一化质量流量分布如图5所示。

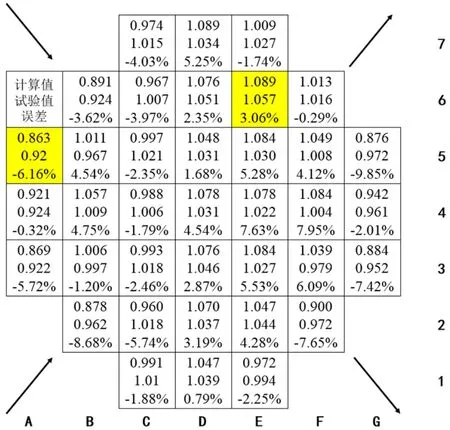
图5 稳态归一化质量流量分布图

从图5可知稳态计算与试验所得数据整体误差小于10%，数值计算方法可以满足流动特性分析要求。

2.2 摇摆模型的验证

选用试验数据进行模拟验证。摇摆周期设置为10s其中摇摆角度分别为10°、15°、20°。从图6中可以得出计算软件与实际符合较好，可以完成摇摆条件冷却剂流动特性分析。

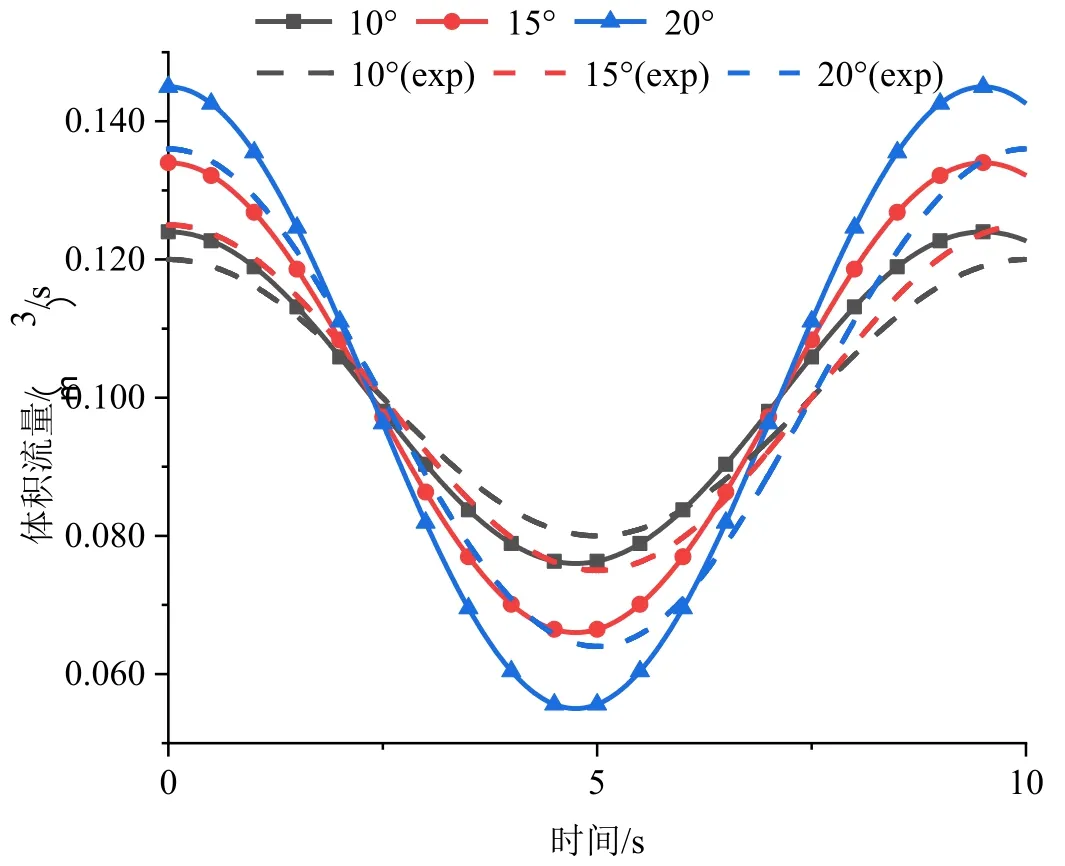
图6 摇摆条件数值计算验证

3.计算结果与分析

利用STAR-CCM+分别为系统添加摇摆周期为10s；摇摆幅度为10°的横摇与纵摇，对比分析反应堆冷却剂堆芯处冷却剂流量变化与流量分布情况。

3.1 横摇与纵摇对堆芯入口冷却剂流量变化的影响

分别取D2、D6、B4和F4处冷却剂流量，分析不同时刻横摇与纵摇对反应堆入口冷却剂流量影响如图7～图10所示。图中横轴为周期，纵轴为该位置冷却剂瞬时质量流量M与该位置冷却剂稳态时质量流量M0的比值。其中D2、D6位置位于纵摇的摇摆轴上，B4、F4位于横摇的摇摆轴上。

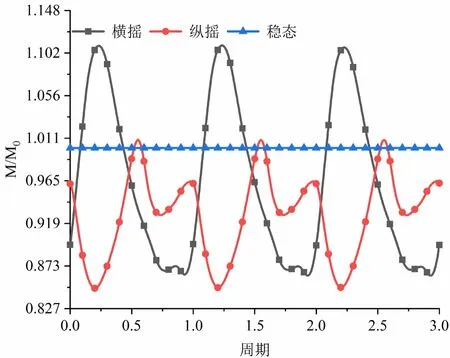
图7 D2处冷却剂流量与时间的关系

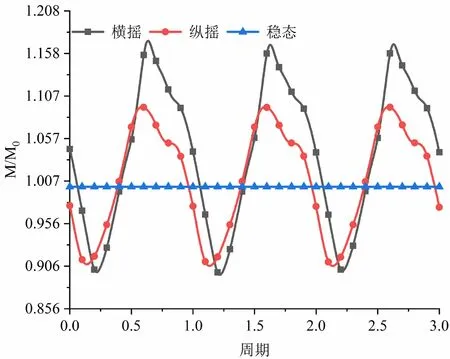
图8 D6处冷却剂流量与时间的关系

图9 B4处冷却剂流量与时间的关系

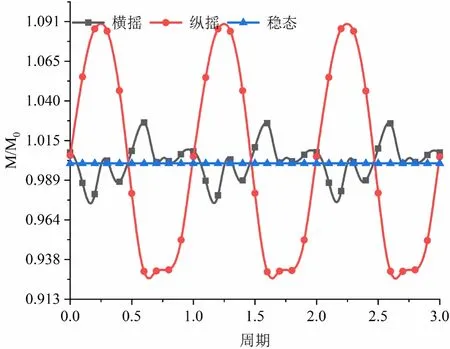
图10 F4处冷却剂流量与时间的关系

系统受横摇作用时，各位置冷却剂随系统摇摆而发生波动，摇摆运动不停止，则流量波动不停止。B4、F4位置的冷却剂流量变化偏离余弦函数。而D2、D6位置冷却剂受横摇影响流量变化符合余弦函数，在摇摆至两侧极限位置时，冷却剂流量波动也到达最大值。对比图7与图10横摇作用下冷却剂流量变化，冷却剂流量波动最大值随距离摇摆轴的垂直距离增加而增加。

与受横摇作用相似，系统受纵摇作用时，各位置冷却剂流量随系统摇摆而发生波动，摇摆运动不停止，则冷却剂流量持续波动。在纵摇作用下，B4、F4位置的冷却剂流量变化符合余弦函数较好，对称轴两侧冷却剂变化相差0.5个周期。冷却剂流量分别于纵摇至前后最大位移处达到波动最大值，波动最大值约为流量的10%。

3.2 横摇与纵摇对堆芯入口冷却剂流量分布的影响

利用不同时刻质量流量的均方差定量分析堆芯入口流量分布是否均匀。公式为：

式中，σ为瞬时堆芯入口质量流量均方差，Mi为燃料组件i入口瞬时质量流量，堆芯入口质量流量。堆芯入口质量流量均方差与时间关系如图11所示。

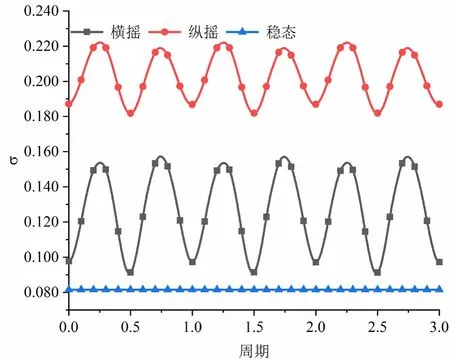
图11 横摇、纵摇条件下冷却剂质量流量均方差与时间的关系

由图11中可知，无论是横摇还是纵摇堆芯入口冷却剂分布都会随时间改变而改变，分别当系统摇摆至正、负波动最大值时，冷却剂的流量均方差达到最大值，此时冷却剂分布最不均匀，而当系统的摇摆角度为0时，冷却剂质量流量均方差最小，冷却剂分布较为均匀。相比于横摇，纵摇对堆芯入口流量分布影响更为明显。这主要是由于冷却剂进入下腔室后分为2个关于x轴对称的漩涡，而漩涡的对称轴与横摇的摇摆轴平行，这就导致摇摆引入的外力对对称轴两侧冷却剂的影响会相互抵消；而纵摇的摇摆轴与漩涡的对称轴为垂直关系，摇摆引入的外力对冷却剂的影响不会减弱，所以，纵摇的堆芯入口冷却剂分布影响较横摇更为明显。