基于改进遗传算法的城轨列车节能运行模型
2019-12-18刘建威常柱刚邓海波于鹏
刘建威,常柱刚,邓海波,于鹏
基于改进遗传算法的城轨列车节能运行模型
刘建威1, 2,常柱刚2,邓海波2,于鹏2
(1. 中南大学 土木工程学院,湖南 长沙 410075;2.长沙市规划设计院有限责任公司,湖南 长沙 410007)
为有效减少城轨列车牵引能耗,以列车动力学理论为基础,以列车运行时分为约束条件,利用改进后的遗传算法,建立单列车节能运行控制模型;通过对城轨列车进行合理分组,将再生制动能量利用转化为制动列车和组内其他加速列车的时间重叠问题,通过改进遗传算法对组内列车的工况序列进行搜索寻优,建立多列车节能运行调度方案;以某14站地铁线数据为例,采用MATLAB仿真求解100列车的运行控制方案。仿真结果表明:该模型可在复杂线路条件下使得城轨列车准时准点停站,在保证不同班次列车间运行互不干扰的同时相互利用其再生制动能量,被利用的再生能量可使总能耗节约17.06%。
城市轨道交通;定时限速约束;再生制动;改进遗传算法;退回重算;列车分组
城市轨道交通系统能耗中的牵引制动能耗占轨道交通系统总能耗的40%左右[1−2]。实际运行过程中,各站点之间每条-曲线则对应着列车在不同线路上特定的运行工况及能量消耗[3]。列车再生制动的能量可供同轨道上的列车牵引利用以减少总体耗能[4]。既有文献对考虑再生能量的城轨列车牵引优化研究较少。本文基于列车动力学理论,选取列车运行时刻为约束条件,以列车牵引耗能为目标函数,采用改进后的遗传算法,分别建立列车运行仿真计算模型、单列车节能运行控制模型和考虑再生制动的多列车节能运行调度方案,采用MATLAB编程求解;以某14站地铁线数据为例,设计100列车的运行控制方案,有效地降低了列车牵引能耗,验证了本文模型的节能效果。
1 单列车节能运行控制模型
首先,建立列车运行仿真模型以求解列车在2个站点间的能耗。该仿真模型以减少牵引能耗为目标,并应满足列车控制的运行时刻(站点间规定运行时间)、速度限制(线路最大限制速度)、边界条件(到达站点处速度为0)和控制变量(工况及工况转换要求)等约束条件要求。依据列车运行仿真模型即可编写程序模拟列车在2站点间的运行过程,求解列车优化控制工况,确定相应的节能控制方案。由于列车能耗模型需要依赖已确定的工况转换序列和工况转换点位置[5],限于转换点搜索过程的复杂性,传统方法难于建立精确的搜索模型[5−7],本文对传统遗传算法进行改进(若完成规定迭代次数后无可行解则增加染色体基因数目重新迭代),构建单列车节能运行控制模型,并以列车牵引耗能为目标函数,实现列车最优-曲线的求解。模型的计算流程如图1。
1.1 单列车运行仿真模型
将城轨列车作为单一质点[1],列车从起始点出发,初速度0=0,给定工况转换序列(包括转换点位置)和线路参数(包括坡度和曲率)使列车运行距离后到达终点站停车(v=0),所用时间为,求这一行驶区间中每一时刻列车的瞬时速度、空间位置及受力情况等参数和列车能耗。定义列车运行控制集合如下:

其中:1,2,…,表示不同级位的列车牵引;0表示列车惰行;−1表示列车制动。
研究表明[8−10],采用图2的列车操纵过程较 节能。
设定牵引加速度百分比的数值以模拟机车在不同牵引控制级位下的牵引力状况,为制动加速度百分比,为工况控制序列,为控制变量(∈),表示对应的列车牵引力,为对应的列车制动力,为列车运行总阻力。考虑到列车在惰行及制动过程中不需提供牵引力,在牵引及惰行过程中不需要制动力得到:

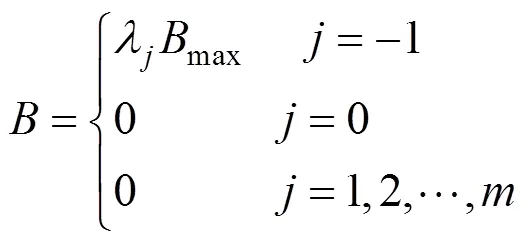
设牵引计算时间步长为Δ,则线路可被分为段(/Δ)。用表示每一时间步长所对应的线路(=1,2,…,),v−1表示该时间步长的初速度,v表示该时间步长的末速度,t表示截止步长一共耗费的时间,s表示截止步长一共行进的距离,列车在每个时间步长内所受外力合力为定值。得到单列车节能运行优化控制模型的基本形式如下。

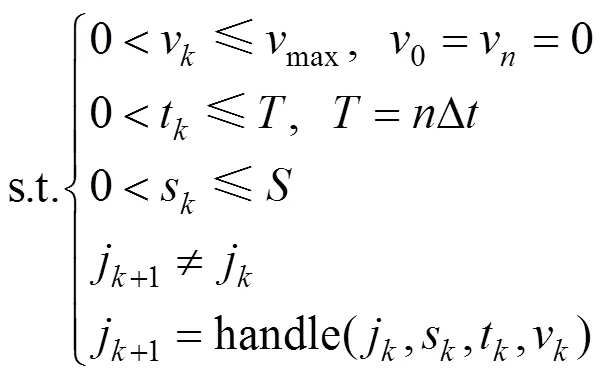
其中:

vmax表示列车运行线路上各区间的限速;jk表示第k个时间步长的控制工况;jk+1表示第k+1个时间步长的控制工况。目标函数的决策变量为工况转换点的位置,是在运算过程中控制模型根据列车的当前工况、运行时刻、空间位置、瞬时速度及受力情况来判断下一步长应采用的工况,由工况转换约束规则及遗传算法搜索决定。
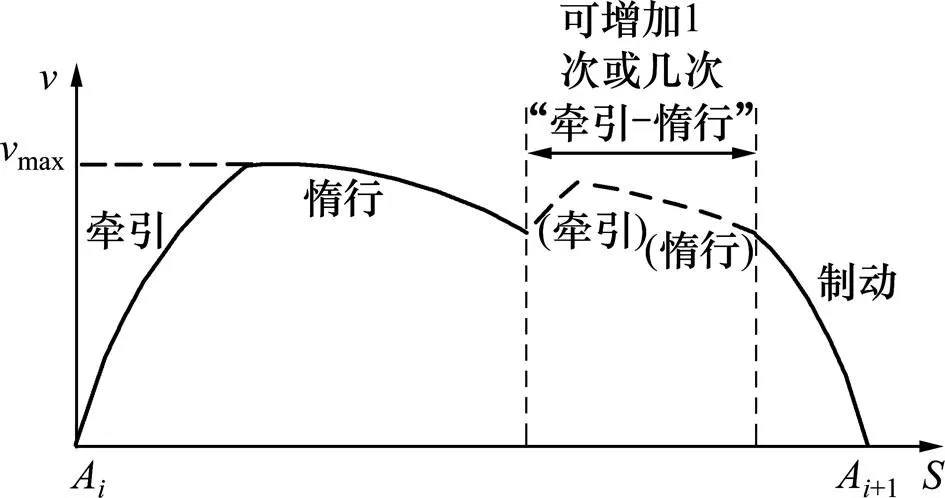
图2 工况控制策略示意图
1.2 合力突变点的处理
根据既有文献假设[11],列车所受牵引力或制动力在经过工况转换点时将发生突变。若在计算过程中仍按假设中合力不变进行计算则会产生较大误差。本文提出基于变更步长的退回重算方法:如图3(a),Δs表示时间步长所对应的列车线路距离,s−1表示步长起始点的距离,s表示步长终止点的距离,表示列车合力变化点位置。

图3 基于变更步长的退回重算原理
得到步长两端点距合力突变点的最短距 离为:
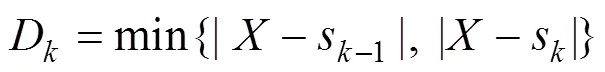
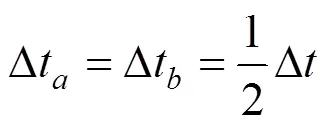

1.3 列车进站制动过程


图4 列车制动过程v-t曲线示意
以制动工况起点处制动力为最大制动能力,经考虑坡度和阻力等因素折减后,可认为列车在人为控制其制动力的条件下,可以维持一个最大的减速度max作匀减速运动;同样,也可在不超过该最大减速度的任意下作匀减速运动。

1.4 改进遗传算法设计
1.4.1 算法引入
列车运行控制方案包括一系列工况,各工况可映射为遗传算法的染色体,工况序列表则对应种群。一个列车运行过程控制方案的一个解用遗传算法的一个个体表示。
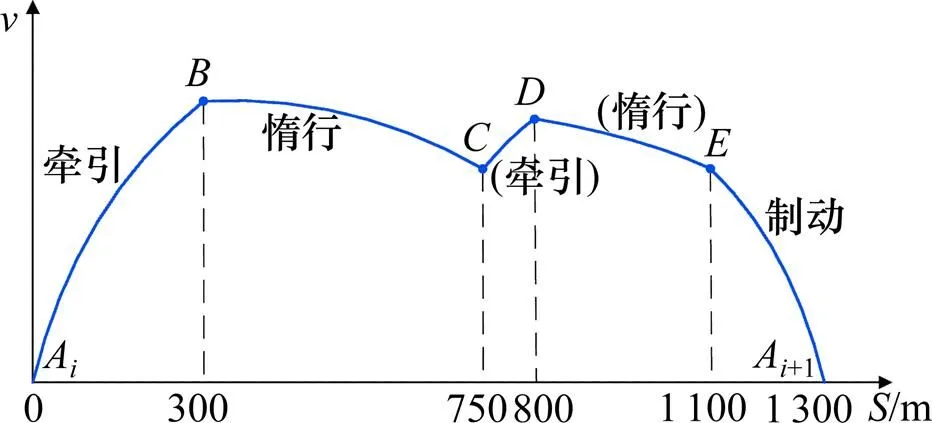
图5 列车工况转换示意图
如图5,每个工况转换点的位置即是一个基因,列车工况转换过程可映射为一个含有4个基因的染色体,表1为各工况转换点位置(采用二进制编码)。

表1 工况转换点与生物遗传概念对应关系
牵引计算时,若1次“牵引−惰行−制动”的仿真过程无法搜索到符合约束条件的可行解,则直接在制动过程前增加一个或多个“牵引−惰行”过程,这实际上增加了染色体的长度。
1.4.2 算法设计
通过前面对遗传算法的改进和分析,得到了本文算法的计算流程:首先,其初始种群生成[12]、选择运算[13−14]和变异运算过程同传统遗传算法;其次,考虑到列车运行控制工况的先后顺序,各工况转换位置受到空间边界和时间约束,故交叉操作的同时应判断各基因是否有效;最后,利用列车运行仿真模型及其约束条件判断是否为有效解,若没有搜索出有效解,则增加染色体基因。
2 多列车节能运行调度方案
制定多列车节能运行调度方案,要同时考虑约束条件下单辆列车在运行过程中消耗的能量,及供电区段内再生能量的利用情况。如图6,列车制动时产生的能量reg可供同区段内牵引状态的列车利用从而减少耗能。

图6 再生能量利用示意图
根据文献[11],再生能量可按下式计算:
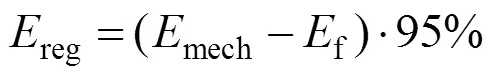
其中:mech表示制动前后的机械能变化量;f表示基本阻力和附加阻力消耗的能量。
再生能量被利用的部分可按下式计算:

其中:brake表示第+1辆列车的制动时长;overlap表示brake与第辆列车加速时间的重合部分。
由于运行过程计算复杂,且城轨列车每日开行多达上百趟班次,要同时进行全局最优搜索几乎是不可能的[7]。因此,本文以单列车节能优化控制模型为基础,对列车进行合理编组,构建多列车节能运行调度方案模型。具体思路如图7。
2.1 列车分组方案
为使相邻列车的制动和牵引过程尽可能重合以达到节能目的,可根据线路情况将列车进行分组。考虑按两两分组共分为G组,每一组组内2列列车的发车间隔h应在满足速度限制的前提下尽量控制在列车站点间运行时间以内,以保证2车牵引和制动时间尽可能重合,各组之间的发车间隔h须能满足规定的发车间隔总时间这一约束条件。将多列车的节能优化问题分解为考虑再生能量利用的2列车工况序列搜索寻优问题,实现对再生能的优化利用。

图7 多列车节能运行调度方案流程图
2.2 列车开行方案
为避免追尾,后车速度应在限制速度lim以 下[15],则2列车间最小间距为:
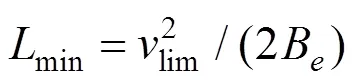
其中:B是列车最大制动加速度。
可得以下限制条件:

根据列车运行-图和最短停站时间min,可反算出满足该条件下2列车N+1和N的最小时间间隔min,即对发车间隔有:
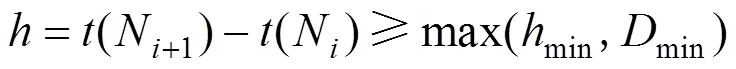
对于首末班车发车时间间隔0有:

因此,的可行域为:
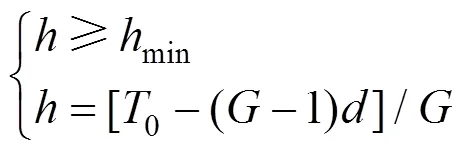
目标函数:
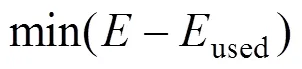
其中:
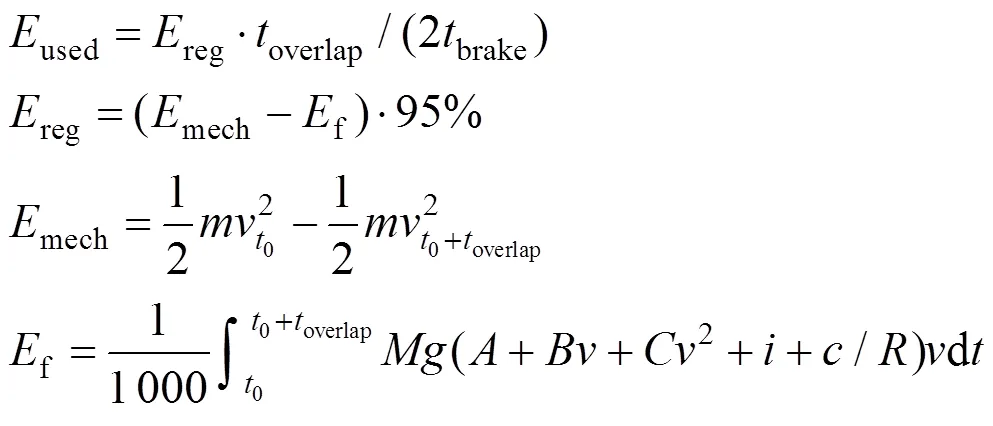
目标函数的决策变量为组内发车间隔h和组间发车间隔h,式中E等式各参数含义见文献[11]。
3 案例分析
3.1 基本信息
以一条全长22.9 km,拥有14个车站的地铁线路为例,考虑100辆列车以时间间隔={1,…,99}(各分量的取值范围为2~11 min)依次从A1站出发途经各站到达A14站,各站停站时间最少30 s,最多45 s,要求首末班车的发车时间间隔为0= 63 780 s,且每辆车首末站间的总开行时间均为定值 2 078 s。
3.2 基于牵引能耗的2站点间单列车节能运行分析
将列车参数及A6-A7站点间线路参数输入列车运行仿真模型,取时间步长Δ=1 s,得到收敛效果较好的遗传算法基础参数,如表2所示。

表2 遗传算法基本参数设定
依据节能策略,A6-A7站点的初始工况序列设为“牵引−惰行−制动”。考虑不同牵引级位下的牵引力传输效率,计算得对应的最优-曲线如图8,可见列车在运行过程中的工况转换序列按“牵引−惰行−制动”操作是可行的。对比可知,在牵引力传输效率=0.8的情况下得到列车最优运行能耗,为7.467 2 kW∙h对应的牵引−惰行工况转换点为140 m,惰行−制动工况转换点为1 067 m。
考虑到实际情况及模型的通用性,进一步计算了二次牵引下(即“牵引−惰行−牵引−惰行−制动”工况转换序列)列车能耗与列车-曲线如图9。对比图8与图9可知,本案例1次牵引的最优解比2次牵引最优解能耗值低,为城轨列车站点间距离普遍较短导致。因此本文统一采用1次牵引工况序列。
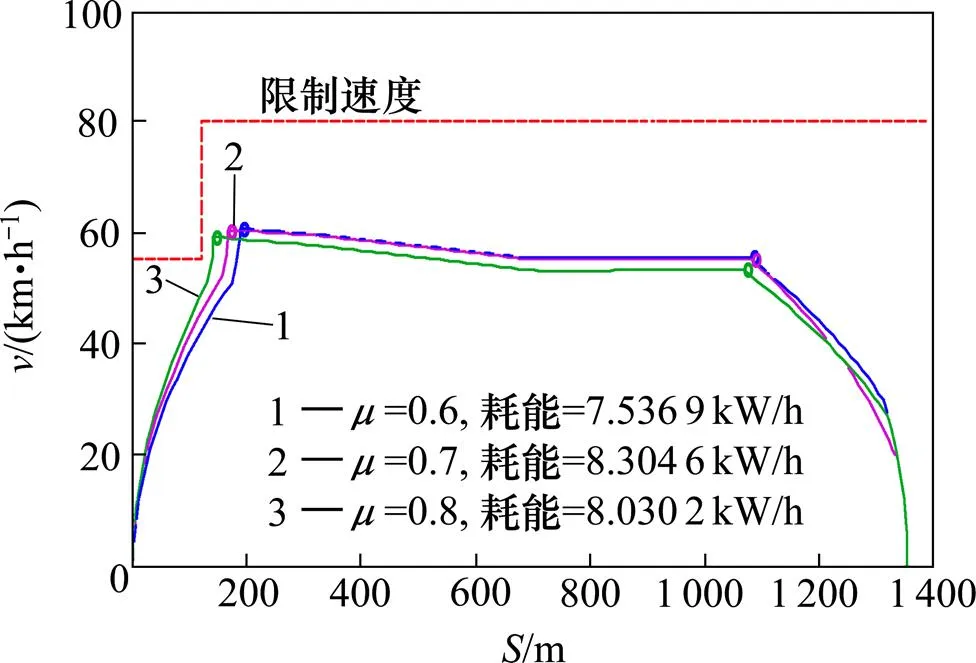
图8 不同牵引级位下采用1次牵引最优V-S曲线
3.3 基于再生制动的多列车全线开行调度方案
根据3.2节所述单列车节能运行控制模型,可得出A1~A14站间的单列车全程运行最优图如图10,并以此作为所有列车的运行图。采用2.1所述方案对列车进行两两分组如图11(图中同颜色的竖粗线表示2列车为同一组,圆弧线代表单列车全程运行图,h为列车的组内发车间隔,h为组间发车间隔),在2.2节的约束条件下以列车运行总耗能为目标函数,采用遗传算法进行优化求解,并从若干可行解中进一步比选出最优解,进而得到多列车全线开行调度方案。得到最优的运行时间间隔为:

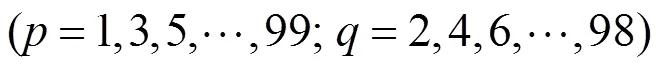
计算得被利用的再生能量可使总能耗节约17.06%,100列列车的最终能耗为9 115.94 kW∙h。

图9 不同牵引级位下采用2次牵引最优V-S曲线

图10 单列车的全程运行最优V-t图

图11 多列车出行分组安排
4 结论
1) 结合列车牵引计算理论设计以时间为步长的城轨列车运行仿真模型,并针对步长中可能出现的合力突变点提出退回重算策略;通过将列车运行过程分解为工况序列且将工况序列映射为染色体,使基于变长染色体的改进遗传算法融入列车仿真模型的求解过程,构建单列车节能运行控制模型。
2) 基于再生能量利用原理、列车运行时分限制以及单列车节能运行模型,对城轨列车两两分组,将多列车的节能优化问题分解为小组内列车的工况序列搜索寻优问题。
3) 以某14站地铁线数据为例,基于单列车的牵引耗能分析,得出城轨列车2站点间采用1次牵引的普遍比2次牵引更节能,进一步求解出单列车全程运行最优图,最终得出100列的全线开行调度方案;被利用的再生能量可使总能耗节约17.06%
4) 模型可在复杂线路条件下使城轨列车准时准点停站,保证不同班次列车间运行互不干扰的同时相互利用其再生制动能量,有效降低列车运行能耗,可供相关案例作为参考。
[1] 顾添慧. 城市轨道交通列控系统牵引制动的计算和研究[D]. 北京: 北京交通大学, 2011.GU Tianhui. Research and caculation on rail transit line braking traction control system[D]. Beijing: Beijing Jiaotong University, 2011.
[2] 喻李葵, 沈杰, 苏博, 等. 牵引策略对动车组运行能耗的影响[J]. 中南大学学报(自然科学版), 2017, 48(1): 262−269.YU Likui, SHEN Jie, SU Bo, et al. Impact of traction strategy on traction energy consumption of CRH[J]. Journal of Central South University (Science and Technology), 2017, 48(1): 262−269.
[3] 李佳杰, 柏赟, 邱宇, 等. 现代有轨电车时刻表与操纵节能协同优化[J]. 铁道科学与工程学报, 2017, 14(7): 1552−1558.LI Jiajie, BAI Yun, QIU Yu, et al. Coordinated optimization of modern tram control and timetable for energy saving[J]. Journal of Railway Science and Engineering, 2017, 14(7): 1552−1558.
[4] 荀径, 唐涛, 宋晓美, 等. 再生制动条件下的城轨列车节能驾驶综合模型[J]. 中国铁道科学, 2015, 36(1): 104−110.XUN Jing, TANG Tao, SONG Xiaomei, et al. Comprehensive model for energy-saving train operation of urban mass transit under regenerative brake[J]. China Railway Science, 2015, 36(1): 104−110.
[5] Fukuhara T, Imai T. Evaluation method of train operation control under gales considering temporal fluctuations of wind velocity[J]. Quarterly Report of RTRI, 2007, 48(3): 148−152.
[6] Ramos G, Leal A F, Ríos M A, et al. Grounding model in multi-train dc traction systems[J]. IEEE Latin America Transactions, 2014, 12(2): 169−175.
[7] 余进, 何正友, 钱清泉. 基于微粒群算法的多目标列车运行过程优化[J]. 西南交通大学学报, 2010, 45(1): 70−75.YU Jin, HE Zhengyou, QIAN Qingquan. Multi-objective train operation optimization based on particle swarm algorithm[J]. Journal of Southwest Jiaotong University, 2010, 45(1): 70−75.
[8] 周艳芳, 周磊山, 乐逸祥. 城市轨道网络换乘站列车衔接同步协调优化研究[J]. 铁道学报, 2011, 33(3): 9−16.ZHOU Yanfang, ZHOU Leishan, YUE Yixiang. Synchronized and coordinated train connecting optimization for transfer stations of urban rail networks[J]. Journal of the China Railway Society, 2011, 33(3): 9−16.
[9] SONG Q, SONG Y D, CAI W. Adaptive back stepping control of train systems with traction/braking dynamics and uncertain resistive forces[J]. Vehicle System Dynamics, 2011, 49(9): 1441−1454.
[10] LUO H, XU H, ZHANG W, et al. Adaptive robust control designed for automatic train operation with guaranteed tracking performance[J]. Sensors & Transducers, 2014, 176(8): 249−256.
[11] 唐海川. 城市轨道交通多列车运行节能优化控制[D]. 成都: 西南交通大学, 2015.TANG Haichuan. Energy-efficient multi-train control in metro transit system[D]. Chengdu: Southwest Jiaotong University, 2015.
[12] WANG S X, ZHANG C Y, JIN L L. A hybrid genetic algorithm for flexible job-shop scheduling problem[J]. Advanced Materials Research, 2013, 889/890(11): 1179− 1184.
[13] ZHOU Y, ZHOU L, WANG Y, et al. Application of multiple-population genetic algorithm in optimizing the train-set circulation plan problem[J]. Complexity, 2017, 2017(7): 1−14.
[14] LI Y, XIN C, WU J, et al. A study of attribute weighted SVM based on Genetic Algorithm[J]. Hebei Gongye Daxue Xuebao, 2012, 41(5): 103−106.
[15] 张永红. 城市轨道交通列车运行图缓冲时间优化方法研究[D]. 长沙: 中南大学, 2013.ZHANG Yonghong. The study on buffer time optimization method of train operation diagram in urban rail transit[D]. Changsha: Central South University, 2013.
Energy-saving operation model for urban rail train based on improved genetic algorithm
LIU Jianwei1,2, CHANG Zhugang2, DENG Haibo2, YU Peng2
(1. School of Civil Engineering, Central South University, Changsha 410075, China;2. Changsha Planning & Design Institute Co., Ltd, Changsha 410007, China)
To reduce the traction energy consumption of urban rail train, the improved genetic algorithm was used for the energy-saving operation control model of single train based on the theory of train dynamics and the constraint condition of train schedule. By grouping the trains reasonably, the regenerative braking energy utilization was transformed into the time overlap between the braking train and other accelerated trains in the group. The improved genetic algorithm was used to search the optimal operating conditions of trains in the group and the energy-saving operation scheduling plan of multiple trains was established. Taking the data of a 14-station subway line as an example, the operation control scheme of 100 train was solved by MATLAB simulation. Simulation results indicate this model can make the urban rail train stop on time in the complex line condition; the schedules of different trains will not be obstructed each other and meanwhile the regenerative brake energy can be utilized interavailability; the regenerative utilized energy can save 17.06% total energy consumption.
urban rail transit; definite time and limited speed; regenerative brake; improved genetic algorithms; return and recalculation; train grouping
U268.6;U268.43
A
1672 − 7029(2019)11− 2881 − 08
10.19713/j.cnki.43−1423/u.2019.11.030
2019−03−04
国家自然科学基金资助项目(50708117)
刘建威(1979−),男,湖南双峰人,高级工程师,博士,从事城市道路与轨道交通研究;E−mail:27362631@qq.com
(编辑 阳丽霞)
