高铁货物运输安全风险识别与计量

张得志，郭瑶微，陈妍，燕春光，祝伟丽

高铁货物运输安全风险识别与计量

张得志1，郭瑶微1，陈妍2，燕春光3，祝伟丽1

(1. 中南大学 交通运输工程学院，湖南 长沙 410075；2. 北京交通大学 交通运输学院，北京 100044；3. 中车唐山机车车辆有限公司，河北 唐山 064000)

基于快速化货物运输中的安全风险因素，构建了基于马尔科夫链的高铁货运安全可靠度计量分析模型，定量分析基于服务供应链视角的高铁货运各环节的安全可靠度；同时，构建基于贝叶斯网络的高铁货运安全风险评价模型，借助GeNIe软件和数学推理得出根节点的概率重要度，甄别影响高铁货运安全的关键指标与关键环节。最后，通过数值仿真验证了模型的有效性，研究结果表明：高铁货物运输安全可靠度与修复率的相关性较大，加强动车组风险识别和处理能力，可有效提升高铁货物运输安全可靠度；规范高铁货运作业、加强安全防范措施和应急水平是保障高铁货运安全的重要措施。

高铁货运；运输安全；运输建模；马尔科夫链；贝叶斯网络

随着社会经济快速发展，快速化货运成为我国物流发展的一个重要方向。铁路快速化货物运输是铁路企业适应现代化物流市场、重塑品牌影响力的重要手段，同时也对铁路货运安全保障提出了更高的要求，如何加强快速化货运安全保障成为值得思索和探究的问题。国内外有关普通铁路货运安全风险问题的研究已经较为全面，涵盖了不同种类的货物运输，并且随着人工智能、物联网和大数据的发展，已经有学者开始研究应用现代物流技术保障铁路货物运输安全。Faeze等[1]利用新型分类框架对铁路运输的运营、维护和安全3个领域下大数据的最新应用进行了全面评估，确定了未来铁路运输系统中大数据分析的研究方向。Bolag等[2]将带有集成传感器的RFID技术应用于铁路货运，对温度、压力、磨损等信息进行监测，实现铁路货运信息化。对于铁路货运安全风险的影响因素和评价方法，杨能普等[3]提出一种定量评估铁路危险货物运输风险的方法，通过构建事故树，结合贝叶斯网络进行定量分析，找到运输过程中的薄弱环节。常青[4]对铁路超限货物进行了安全影响因素分析，在事故树的基础上运用模糊贝叶斯方法进行安全评价，找到了影响超限货物运输安全的关键环节。薛红兵[5]分析了铁路货运安全的影响因素，从人员、设备、规章制度三方面建立了铁路货运安全评估指标体系，利用层次分析法构建了安全评估模型，并对实例进行了安全评估。黄兴建等[6]从设备、人员、货物、管理和环境五个方面构建了铁路货运安全评价指标体系。在利用高速铁路开展快捷货物运输方面，Kazuhiko等[7]研究了轨道变化对高速铁路列车脱轨事件的影响。Ertem等[8]调查了使用高速列车(HST)来运输货物的情况，提出HST调度模型，并通过土耳其高速铁路网和火车组进行实验性测试。Baldini等[9]提出一种基于GSM-R实时采集和传输高速铁路基础设施信息的方法，达到监测预警的目的，实现高速铁路基础设施安全。王洪德等[10]分析了高铁运营过程中的三种主要风险事件，用事故树对各风险事件进行定性分析，构建了高铁运营安全Bow-tie模型。朱海宏等[11]基于事故树引入贝叶斯网络技术，以CTCS-2级列控系统为例对高速铁路控制系统的安全性进行了评估。综上所述，目前国内外与铁路货运安全评价和高铁安全相关研究的角度较为单一，多是从环境、人员、设备、管理等方面对安全影响因素进行分析，缺乏基于全息化视角对整个物流服务过程的安全保障研究，高铁货运过程中安全风险的快速辨识和风险评估技术是轨道交通领域的重大技术瓶颈[12]。基于此，本文在宏观和微观层面分别建立了基于马尔科夫链的高铁货运安全可靠度计量模型和基于贝叶斯网络的高铁货运安全风险评价模型。首先，引入马尔科夫链，对高铁货运各地点环节的安全风险值进行计量分析。再将事故树与贝叶斯网络结合，构建高铁货运安全风险评价模型，甄别出影响高铁货运安全的关键指标和关键环节，从而科学合理的对快速化货物运输中的风险因素进行防范和控制。

1 模型构建

1.1 基于马尔科夫链的高铁货运安全可靠度计量分析模型

2.1.1 建立状态转移模型

物流服务的安全可靠度为物流服务系统在规定的时间和条件下，准确、可靠、安全地履行物流服务承诺的能力。本文运用马尔科夫模型对快速化货物运输物流服务全过程进行安全性和可靠性分析。基于高铁货运中各地点和运输环节，研究货物自身状态、物流活动和运输设施三方面在整个物流服务过程中的安全可靠度。每一时间段，货物本身、物流活动和运输设施的状态只与该时间段作业环节的状态有关，与该时间段以前的作业环节状态无关，符合马氏链“无后效性”特征，因此分别建立“货物状态链”、“物流活动链”和“运输设施链”3条马氏链。在每一地点环节，建立状态转移模型如图1所示，并做出如下假设：

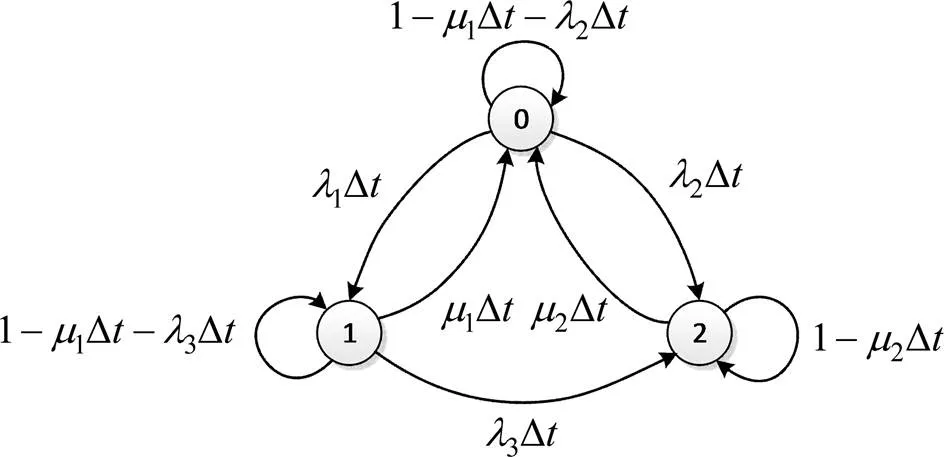
图1 马尔科夫状态转移过程

1) 研究对象在每一时刻可能处于3种状态：0状态：安全状态，此状态下研究对象无任何异常发生；1状态：“亚安全”状态，此状态研究对象出现异常情况但无风险事故发生，动车组可正常运行，但运行品质较差；2状态：故障/风险状态，此状态下研究对象出现异常情况，且引起较为严重的风险事故发生。

2) 假设研究对象可修复，即研究对象在1和2状态下，通过紧急处理可变为安全状态。

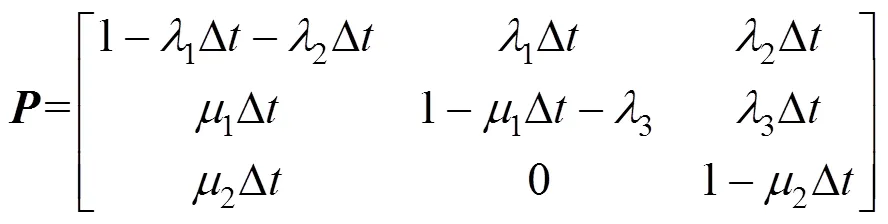
2.1.2 状态转移矩阵的平稳分布

依据式(3)求解得到各状态的平稳分布如式(4)所示：

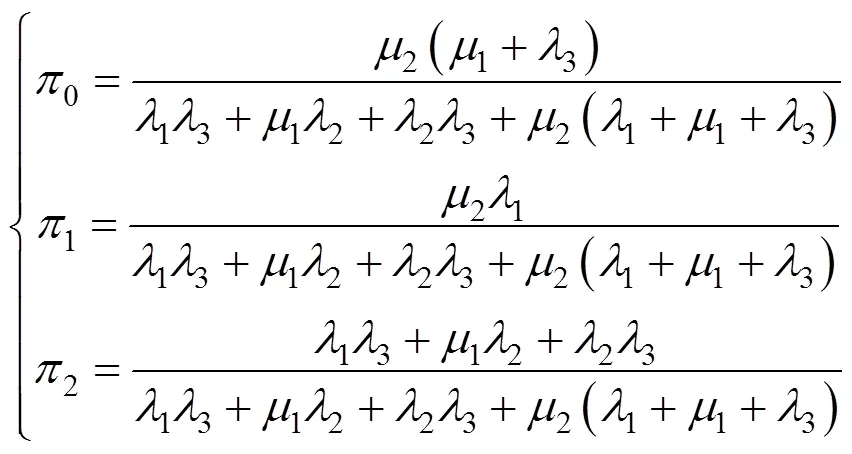
2.1.3 整个货运过程安全可靠度

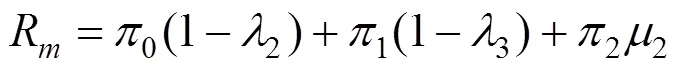
随着货运流程的进行，风险不断累积，整个货运流程的安全可靠度为：

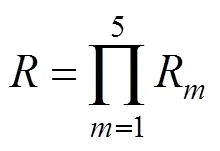
2.2 基于贝叶斯网络的高铁货运安全风险评价模型

本文将考虑因果关系的事故树映射为贝叶斯网络，建立贝叶斯网络拓扑结构。

2.2.1 建立事故树

在事故树中，将高铁货运安全风险(0)作为顶上事件置于事故树第一行；找出导致此顶上事件的各个因素，作为中间事件放于第二行，并用适合的逻辑符号与顶上事件相连接；依此类推，自上而下找出引起故障的因素，直到找出不能分解的因素作为基本事件。本文从“货物−车辆−物流活动”全方位出发，对影响货物自身状态(1)、物流活动(2)和运输设施(3)的因素进行筛选，构建如图3所示的事故树：

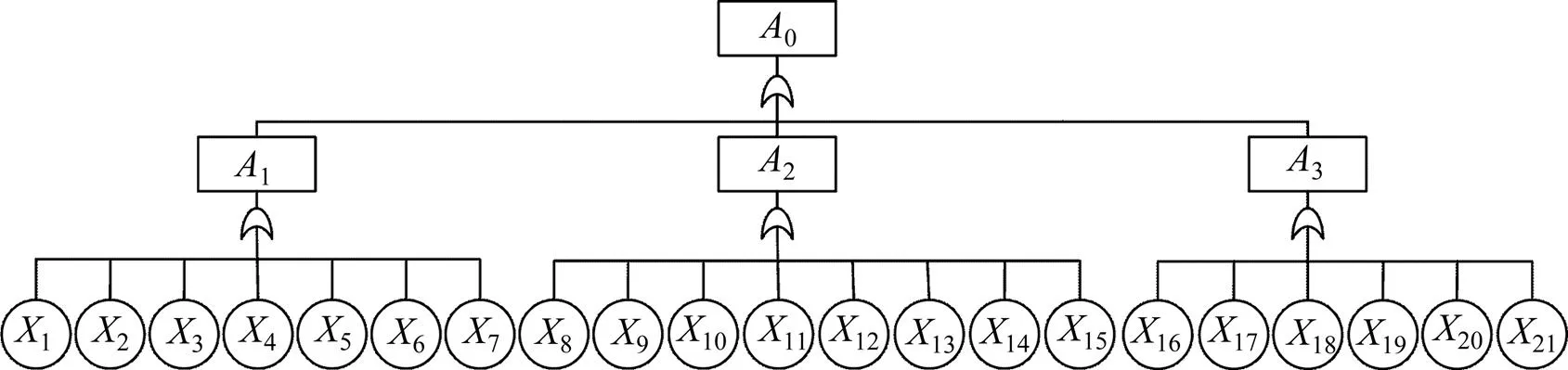
图3 高铁货运安全风险事故树

事故树中基本事件如表1所示。

2.2.2 事故树映射为贝叶斯网络

根据事件、逻辑门、节点的映射关系，将事故树映射为贝叶斯网络如图4所示。

各节点变量值域为[0,1]，其中0表示无风险；1表示存在风险，即高铁货运过程中该安全评价指标发生风险，并导致风险事件发生；在[0,1]中取值，表示相应风险发生的可能性。

表1 事故树基本事件对应序号表

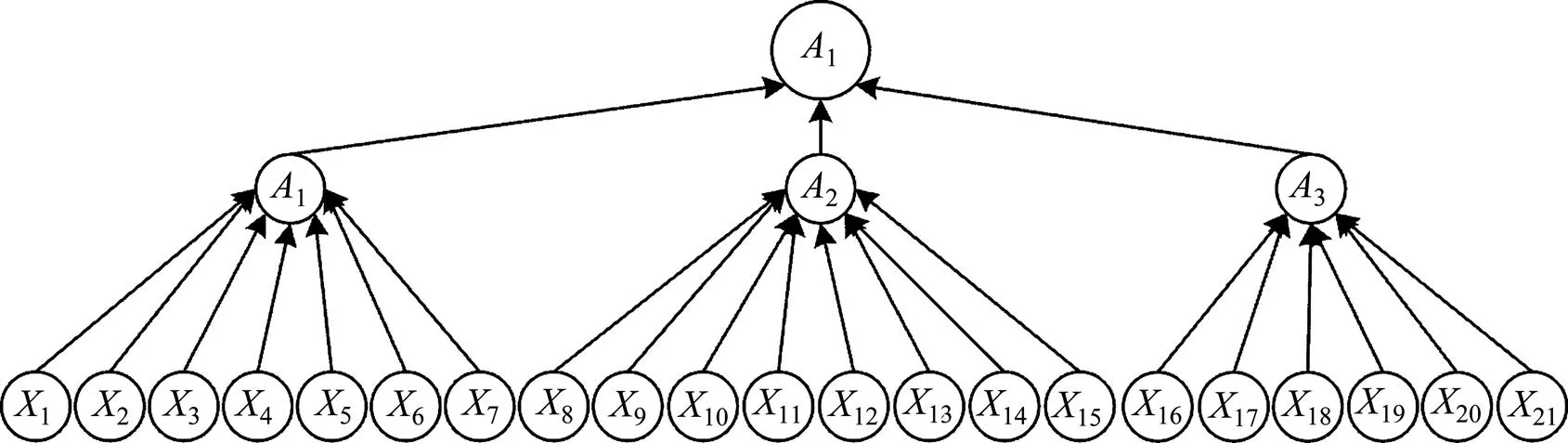
图4 高铁货运安全风险贝叶斯网络

2.2.3 贝叶斯网络节点参数设定

为进行安全风险评价，需要对贝叶斯网络进行节点参数的设定，即非根节点(顶上事件和中间事件)的条件概率和根节点(基本事件)的先验概率，再由贝叶斯网络推理得出最后结果，推理过程由GeNIe软件完成。

1) 非根节点的条件概率

由上节可知，贝叶斯网络是由表示因果关系的事故树映射而来，如果各个子节点的父节点存在值域为1的节点，该子节点必然发生，有下述条件概率公式：

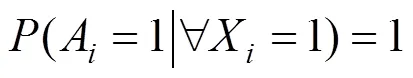
2) 基于专家意见法的根节点先验概率

(10)

根据概率标度尺[14]划定如表2所示的4个专家评定等级，各区间中间值为具体评价值。

表2 专家评价区间值

因此，根据表2和式(10)可计算出条件概率，然后根据专家评价表，推理更新对应根节点的先验概率。本文在GeNIe软件中将贝叶斯网络模型中的货物自身安全、物流活动安全、运输设施安全建立为3个子模型，由GeNIe软件完成根节点先验概率的推理。

2 模型仿真与分析

2.1 基于马尔科夫链的高铁货运安全可靠度计量分析模型的应用

2.1.1 运输设施马氏链模型仿真

1=[0.956 9 0.946 9 0.901 2 0.933 7 0.916 2 0.931 1 0.952 9 0.916 6 0.926 3 0.965 4]

2=[0.910 7 0.996 2 0.900 5 0.977 5 0.981 7 0.986 9 0.908 4 0.940 0 0.926 0 0.980 0]

1=[0.021 6 0.045 5 0.009 1 0.013 2 0.007 3 0.006 8 0.043 5 0.029 0 0.027 5 0.007 2]

2=[0.042 7 0.031 1 0.017 5 0.025 7 0.020 1 0.003 8 0.012 0 0.006 2 0.009 2 0.012 0]

3=[0.034 5 0.037 4 0.022 5 0.004 2 0.011 4 0.007 6 0.041 3 0.026 9 0.003 9 0.022 1]

将上述值代入式(4)求出稳态概率：

0=[0.935 1 0.926 6 0.971 3 0.961 2 0.972 4 0.989 0 0.944 4 0.963 2 0.961 9 0.980 6]

1=[0.001 0 0.001 3 0.000 2 0.000 4 0.000 2 0.000 0 0.000 5 0.000 2 0.000 3 0.000 1]

2=[0.044 6 0.030 5 0.019 2 0.025 3 0.020 0 0.003 9 0.014 3 0.007 2 0.009 7 0.012 2]

依据式(5)求得各地点的安全可靠度如下：

=[0.936 7 0.929 5 0.971 7 0.961 6 0.972 6 0.989 1 0.946 6 0.964 2 0.962 3 0.980 9]

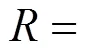
将各地点安全可靠度R分别与各状态转移参数进行二次函数拟合，并求取各拟合函数相关系数的和，得如下结果：

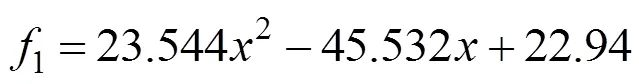
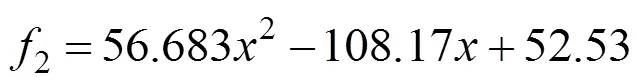
3.1.2 结果分析

1) 动车组运输全过程运输设施的安全可靠度分别为0.79和0.85，均在0.8左右，相差不大，说明模型适用性较强。

2) 在稳态下，动车组“安全”状态概率0在0.9以上，远大于“亚安全”状态概率1和“故障”状态概率2，且个地点环节安全可靠度在0.9以上，说明稳态概率下运输车辆的安全可靠度很高，即利用高速铁路动车组进行货物运输安全可靠度很高。

3) 通过相关系数和的比较可以发现各地点安全可靠度与修复率1和2的相关性较大，说明运输设施发生风险情况后的处理是否及时、有效对高铁货物运输安全影响很大，需要作业人员具有较强的应急处理能力，及时处理风险状况；而与1，2和3的相关性非常小，主要因为在一次高铁货物运输过程中动车组发生故障的概率很小。因此铁路企业需要加强运输过程中对列车运行状态的监控，一旦发现风险情况，及时采取措施使列车转为安全。

物流活动和货物状态马氏链模型的应用与运输设施链的计算分析过程基本相同，此处不再进行分析。

2.2 基于贝叶斯网络的高铁货运安全风险评价模型应用

2.2.1 贝叶斯网络因果推理分析

贝叶斯网络中根节点的先验概率通过专家意见法来进行确定。在GeNIe软件操作界面中提前设置好各节点参数，包括根节点发生风险的先验概率和非根节点的条件概率。在操作时设置好每个根节点的专家评判结果，然后进行推理更新。根据推理更新结果，整理得到根节点先验概率如表3中第3列所示，非根节点风险概率仿真结果如表4第3列所示。

表3 根节点风险概率仿真结果

表4 非根节点风险概率仿真结果

2.2.2 贝叶斯网络诊断推理分析

在高铁货运安全风险决策与控制的过程中，通过诊断推理分析，可以确定当高铁货物运输发生风险时各基本事件即根节点发生风险的概率。从而进行各基本事件的重要度分析，得到影响高铁货运安全的关键指标。

在GeNIe软件中，保持专家评判意见结果不变，设置目标节点“高铁货运安全”为证据节点，假设其一定会发生风险，即风险概率值为1，然后通过更新进行诊断推理得出根节点和中间节点的后验概率，即在高铁货运发生安全风险时各指标发生风险的概率。根节点和中间节点后验概率分别如表3和表4第4列所示，将根节点后验概率整理成如图5所示的折线统计图。可见，最容易发生安全风险的是物流活动中作业程序规范性和安全防范措施两项指标，风险概率值已经超过50%。

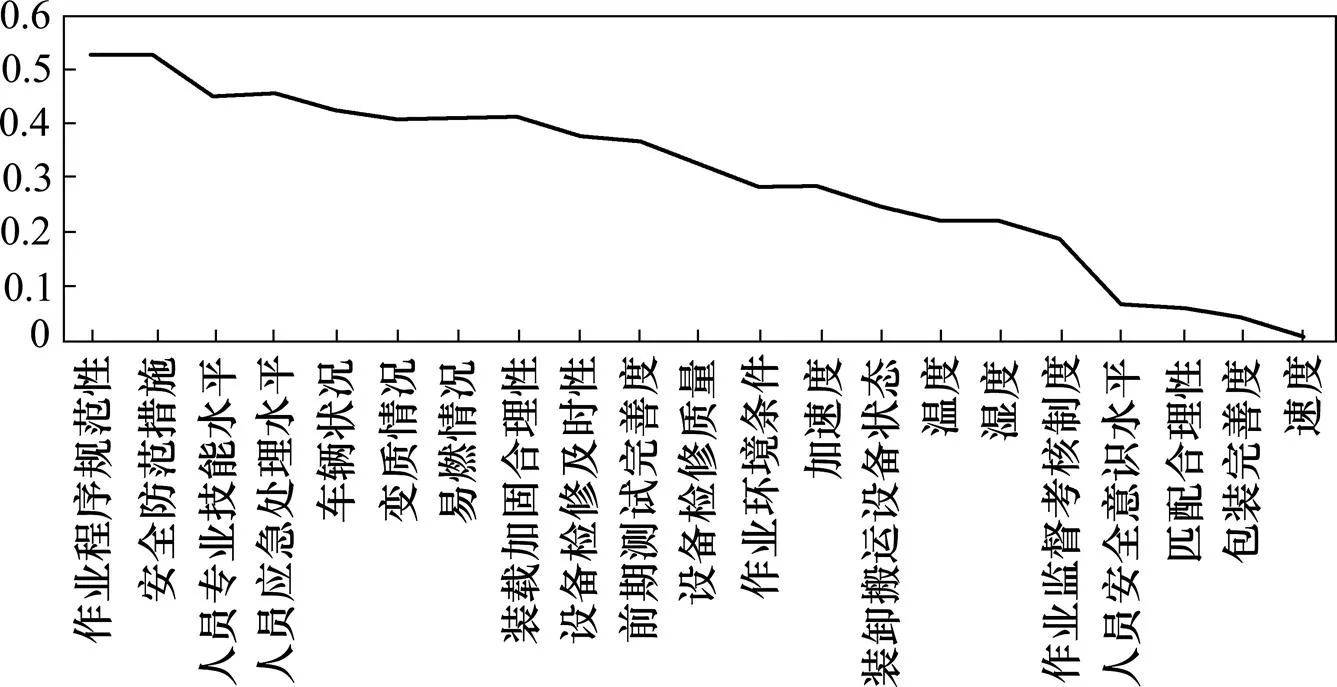
图5 根节点后验概率

2.2.3 根节点概率重要度分析

基本事件发生概率的变化引起顶上事件发生概率的变化程度称为概率重要度。因此概率重要度能够有效反应各根节点的重要程度，通过降低重要程度高的根节点的发生概率可以有效控制顶上事件的发生概率。根节点概率重要度I的计算公式 如下[3]：

由式(12)中基本事件概率重要度的排序结果我们可以发现作业程序规范性、安全防范措施、人员专业技能水平这三项指标概率重要度较高，需要特别加以防范和控制。根据模型仿真结果，对高铁货运企业提出以下管理启示：

1) 规范高铁货运作业，建立标准化作业流程和专门化作业标准。完善相应的软硬件配套设施，在此基础上，严格按照作业标准进行规范作业。

2) 加强安全防范措施，制定完善的安全管理标准，利用现代物联网技术加强对货物、车辆、物流活动等技术状态的监控，完善预警系统建设。

3) 加强对高铁货运相关作业人员的培训，提升作业人员专业技能水平和应急处理能力。对作业质量进行及时监督和考核，确保作业人员的专业性。

3 结论

本文结合马尔科夫链和贝叶斯网络，构建了基于全息化视角的快速化货物运输的安全风险识别与计量模型，在分析高铁货运各环节的安全可靠度的基础上，借助GeNIe软件和数学推理得出根节点的概率重要度，甄别出最容易发生安全风险的关键指标。本文的主要研究结论如下：

1) 物流活动在各地点环节的安全可靠度与修复率的相关性更大，紧急处理风险状况的能力对物流活动安全可靠度发挥着至关重要的作用。

2) 高铁货运中最容易发生安全风险的是作业程序规范性、安全防范措施和人员专业技能水平等指标，需要特别加以防范和控制。

3) 规范高铁货运作业、加强安全防范措施、提升作业人员专业技能水平和应急处理能力、对作业质量进行及时监督和考核是保障高铁货运安全的重要措施。

[1] Ghofrani F, He Q, Goverde R M P, et al. Recent applications of big data analytics in railway transportation systems: A survey[J]. Transportation Research Part C Emerging Technologies, 2018, 90: 226−246.

[2] Balog M, Mindas M. Informatization of Rail Freight Wagon by Implementation of the RFID Technology[M] Germany: Springer International Publishing, 2016: 592− 597.

[3] 杨能普, 杨月芳, 冯伟. 基于模糊贝叶斯网络的铁路危险货物运输过程风险评估[J]. 铁道学报, 2014, 36(7): 8−15. YANG Nengpu, YANG Yuefang, FENG Wei. Risk assessment of railway dangerous goods transport process based on fuzzy bayesian network[J]. Journal of The China Railway Society, 2014, 36(7): 8−15.

[4] 常青. 铁路超限货物运输安全影响因素分析与安全评价[D]. 北京: 北京交通大学, 2015. CHANG Qing. The analysis and safety assessment of railway out-of-gauge goods transportation safety influence factors[D]. Beijing: Beijing Jiaotong University, 2015.

[5] 薛红兵. 基于AHP的铁路货运风险评估模型[J]. 科技广场, 2015(10): 206−209. XUE Hongbing. Risk assessment model of railway freight transportation based on AHP[J]. Science Mosaic, 2015(10): 206−209.

[6] 黄兴建, 王伟. 基于动态模糊理论的铁路货运安全评价研究[J]. 铁道科学与工程学报, 2016, 13(7): 1420− 1425. HUANG Xinjian, WANG Wei. Railway freight safety evaluation based on dynamic fuzzy theory[J]. Journal of Railway Science and Engineering, 2016, 13(7): 1420−1425.

[7] Nishimura K, Terumichi Y, Morimura T, et al. Analytical study on the safety of high speed railway vehicle on excited tracks[J]. Journal of System Design and Dynamics, 2010, 4(1): 211−225.

[8] Ertem M A. Keskin Ozcan M. Freight transportation using high-speed train systems[J].Transportation Letters, 2016, 8(5): 250−258.

[9] Baldini G, Fovino I N, Masera M, et al. An early warning system for detecting GSM-R wireless interference in the high-speed railway infrastructure[J]. International Journal of Critical Infrastructure Protection, 2010, 3(3/4): 140− 156.

[10] 王洪德, 张艳潮, 李斯. 基于Bow-tie模型的高铁运营安全风险分析[J]. 辽宁工程技术大学学报(自然科学版), 2017, 36(7): 767−772. WANG Hongde, ZHANG Yanchao, LI Si. Safety risk analysis of high-speed train operation based on Bow-tie model[J]. Journal of Liaoning Technical University, 2017, 36(7): 767−772.

[11] 朱海宏, 徐中伟, 梅萌, 等. 基于贝叶斯网络的高铁系统概率安全评估方法研究[J]. 计算机应用与软件, 2011, 28(3): 26−28, 31. ZHUN Haihong, XU Zhongwei, MEI Meng, et al. Research on probabilistic safety assessment in railway system based on Bayes networks[J]. Computer Applications and Software, 2011, 28(3): 26−28, 31.

[12] 贾利民, 秦勇, 王莉. 轨道交通科技发展的方向与任务[J]. 北京交通大学学报, 2016, 40(4): 25−31. JIA Limin, QIN Yong, WANG Li. Scientific and technological innovation of rail transportation—trends and tasks[J]. Journal of Beijing Jiaotong University, 2016, 40(4): 25−31.

[13] 石坤, 张永进, 孙超勇. 基于马尔科夫链的驾驶行为可靠性分析[J]. 机械研究与应用, 2017, 30(6): 49−52. SHI Kun, ZHANG Yongjin, SUN Chaoyong. Reliability analysis of driving behavior based on the Markov Chain[J]. Mechanical Research & Application, 2017, 30(6): 49−52.

[14] Witteman C, Renooij S. Evaluation of a verbal–numerical probability scale[J]. International Journal of Approximate Reasoning, 2003, 33(2): 117−131.

[15] 王华胜, 李昊, 朱庆龙, 等. 动车组故障率统计分析方法[J]. 中国铁道科学2018,39(1): 88−92. WANG Huasheng, LI Hao, ZHU Qinglong, et al. Statistical analysis method for fault rate of EMU[J]. China Railway Science, 2018, 39(1): 88−92.

Security risk identification and measurement of high-speed-rail freight transportation

ZHANG Dezhi1, GUO Yaowei1, CHEN Yan2, YAN Chunguang3, ZHU Weili1

(1. School of Traffic & Transportation Engineering, Central South University, Changsha 410075, China;2. School of Traffic and Transportation, Beijing Jiaotong University, Beijing 100044, China;3. CRRC Tangshan Co., Ltd, Tangshan 064000, China)

Based on the safety risk factors in rapid freight transportation, this paper constructed a safety reliability measurement model of high-speed rail freight based on Markov chain, and analyzed the safety reliability of all links of high-speed rail freight quantitatively based on service supply chain perspective. Meanwhile, this study constructed a high-speed rail freight safety risk assessment model based on Bayesian network and determined the probability importance of the root node by means of GeNIe software and mathematical reasoning, to father identify the key indicators and key links that affect the safety of high-speed rail freight. Finally, numerical simulation was conducted to verify the validity of the model, the research results show that: the safety reliability of high-speed rail freight transportation is highly correlated with the repair rate, strengthening the risk identification and processing capability of EMU can effectively improve the safety and reliability of high-speed rail freight transportation; standardizing high-speed rail freight operations, strengthening safety precautions and emergency level are important measures to ensure the safety of high-speed rail freight.

high-speed rail freight; transport security; transport modelling; Markov Chain; Bayesian network

U298.1

A

1672 − 7029(2019)11− 2676 − 08

10.19713/j.cnki.43−1423/u.2019.11.005

2019−06−13

国家重点研发计划资助项目(2017YFB1201304)

张得志(1976−)，男，湖南祁东人，教授，博士，从事物流系统优化研究；E−mail：dzzhang@csu.edu.cn

(编辑 蒋学东)