侧风下高速列车临界倾覆风速研究

刘荣，姚松，许娇娥

侧风下高速列车临界倾覆风速研究

刘荣1, 2, 3，姚松1, 2, 3，许娇娥1, 2, 3

(1. 轨道交通安全教育部重点实验室，湖南 长沙 410075；2. 轨道交通安全关键技术国际合作联合实验室，湖南 长沙 410075；3. 轨道交通列车安全保障技术国家地方联合工程研究中心，湖南 长沙 410075)

采用数值模拟方法计算横风下高速列车的气动力及力矩系数，利用EN14067的五质量模型研究横风下车辆临界倾覆风速曲线及不同参数对其倾覆的影响。研究结果表明：临界倾覆风速随着车速的增大而减小，随着风向角的增大先减小后增大，最小值在 80°左右时出现，且随着未平衡横向加速度增大而减小。五质量模型中增加考虑的点头力矩和摇头力矩对临界倾覆风速有一定影响，其中若不考虑点头力矩，设置车辆临界风速限制时偏高，对于车辆运行安全性有不利影响。一系悬挂和二系横向刚度对倾覆系数影响不大。随着二系垂向刚度增加，前转向架轮对倾覆系数减小，后转向架增大。横向止挡间隙增大前后倾覆系数均增大。当抗侧滚扭杆减小到原值60%以上时倾覆系数略有增大，幅度不超过10%。车辆质心越偏向车辆前端时，前倾覆系数增加，后倾覆系数减小。

高速客车；横风环境；五质量模型；临界倾覆风速

随着列车发展趋向更高速度且轻量化。横风下的列车气动问题越显突出，列车空气动力学性能恶化，影响列车横向稳定性，甚至可能使列车脱轨乃至倾覆[1−3]。世界上也多次出现由于强风作用导致列车事故的案例[4]。因此，研究大风条件下列车运行安全速度限值及影响因素是必需的。国内外学者提出了一些能够评估铁路车辆在倾覆风险方面的运行安全性的方法。“临界倾覆风速”是评价列车横风安全性的重要指标之一。国枝正春[5]提出了作用于车辆上外力的静态平衡方程，即国枝正春式。日比野有等[6]在国枝式基础上修正形成了更加详细的详细解析式法。Thomas等[7]运用多体仿真方法模拟研究了轨道弯曲、轨道不平顺、车体横移等影响因素对列车侧风稳定性的影响。Baker等[8−10]采用动模型风洞试验方法研究了列车横风气动特性，并通过静态列车模型研究了挡风屏障对列车抗倾覆性能影响。欧洲标准EN14067中提出了计算列车特征风速曲线的方法：三质量方法，五质量方法(改进的准静态方法)以及依靠时间域的多体系统动力学仿真方法。上述方法中常用的有详细解析式法、三质量方法和多体仿真方法[11]。多体动力学仿真方法是目前相对来说考虑因素最全面，计算临界风速最为准确的方法；详细解析式法和三质量模型方法虽然简单易推导、考虑因素较少，但是其计算简便，容易定量把握要素影响；五质量模型方法相对来说考虑因素较为全面，更贴近实际，且相比多体动力学仿真方法要简单，因此本文选取较少使用研究的五质量模型方法计算国内某型高速列车临界倾覆风速，以及气动力和车辆参数对列车运行倾覆性能的影响。

1 列车气动性能数值模拟

1.1 高速列车数值计算模型建立

计算采用流体力学软件STAR-CCM+进行数值模拟。为了与风洞试验结果进行对比，采用一节半列车。模型列车周围的局部区域、尾部的尾流区域、背风侧区域等均加密网格，设置4个网格控制体，如图1所示。采用RANS方法SST-模型，二阶中心差分格式扩散项，对流项首先使用一阶迎风格式进行离散，再采用二阶迎风格式[12]。使用SIMPLE法耦合压力−速度场，用迭代法修正压力。计算给定空气来流速度为60 m/s。

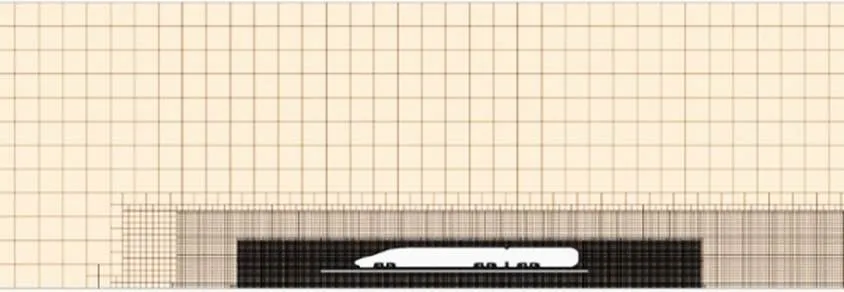
图1 体网格模型截面

1.2 风洞试验

为了确定数值模拟方法对高速列车侧风安全性分析的适用性及检验数值模拟的准确性，将风洞试验结果与数值模拟结果进行对比分析。在德国DNW风洞试验中，列车模型简化了转向架，完整的几何模型符合EN14067-6:2010要求。列车模型由一节头车加一节中间车的一半组成，缩尺比例为1:15。模型试验中测定了升力系数，阻力系数，侧向力系数，俯仰力矩系数，侧偏力矩系数等气动力系数，计算公式如下：

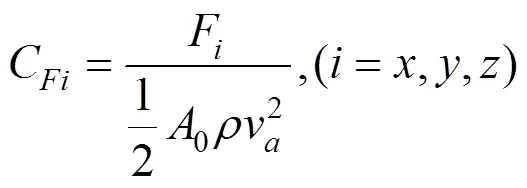
式中：为大气密度；0和0分别为列车参考面积和长度；i和M分别为列车所受相应气动力和力矩；v为作用在车辆上的合成速度，在CFD模拟中也为相对于车辆的空气来流速度。其可以分解为车速v和风速v，为风向角，而侧滑角为车辆合成速度与车辆运行方向夹角，速度三角形如图2所示。

图2 速度三角形分解

将模型试验与数值模拟的结果进行对比，表1为侧滑角为10°时的结果对比。数值模拟与模型试验的气动力及力矩系数的误差在10%以内，在工程误差允许范围之内。存在误差的主要原因有：试验模型的简化(转向架)，列车模型与地面相对运动的差异(地面效应模拟)，湍流模型以及数值计算采用的一些假设等。由此可见，数值模拟方法适用于计算气动载荷系数。

表1 数值计算与试验结果对比

1.3 CFD计算结果

通过对列车的气动性能数值模拟仿真，得到了横风下列车运行时的气动力及力矩系数。不同侧滑角(0°~90°)的侧风环境下列车气动力系数如图3 所示。

图3 列车气动力系数

由图3可以看出，除了点头力矩变化规律较复杂，其他力/力矩系数变化规律简单：侧向力系数、倾覆力矩系数的数值大小均随着侧滑角的增大先增大后减小，且最大系数出现在70°左右。倾覆力矩主要与侧向力大小有关，因此两者变化规律相似。升力系数和摇头力矩系数的绝对值大小随着侧滑角的增大先增大后减小，其数值最大出现在风向角为40°~50°左右。点头力矩系数的变化规律比较复杂，其数值最大出现在风向角40°左右。

2 列车临界倾覆风速计算方法

2.1 临界倾覆风速定义

临界倾覆风速是车辆受到横风后开始发生侧滚时的风速。假如车体受到横风施加的外力，在最不利情况下，迎风侧轮重达到一定临界值，继而若风速继续增大则将引起车辆倾覆，将达到该临界值时的风速定义为临界倾覆风速。EN14067-6标准中将轮轨力相对于静态轮轨力的减少值Δ和静态轮轨力之比作为倾覆判定指标，且在减载率大于0.9时认为车辆运行有倾覆风险。

2.2 五质量模型方法

EN14067-6五质量模型方法(改进的准静态方法)是一种考虑车辆主要部件运动学的静态方法，不考虑减振器等引起的动态作用，得到的临界风速一般小于多体动力学软件方法得到的结果，偏保守。该模型适用于具有两个转向架且不考虑相邻车辆或转向架的车辆。本文研究的高速列车满足该方法适用条件。

该方法采用耦合元件连接集中质量，模型(见图4)共包括5个质量块，车体(CB)、前转向架(BG1)、后转向架(BG2)和前后转向架轮对(WS1，WS2)，一系和二系悬挂位于这些质量块之间，构建为具有一定刚度的弹簧单元。此外若有抗侧滚扭杆也应构建为位于车体和转向架中间的具有绕轴旋转刚度的扭杆。系统坐标如图所示，方向为车辆运行方向，为车辆横向，为垂向。车体具有5个自由度，沿和方向的平移和绕所有轴旋转的自由度。转向架具有3个自由度，沿和方向的平移和绕列车运行方向旋转的自由度。轮对具有0个自由度。系统整体共有11个自由度。

在五质量模型建立中，需要计算不同工况下的车辆平衡位置，平衡位置需要由作用在车辆上的外力确定。在列系统方程组时，需要考虑的力和力矩有：质量力、弹性力和气动力。质量力的计算与重力加速度和未被平衡加速度有关。弹性力的确定与变形量相关，除了一二系弹簧力之外，还应考虑车体和转向架之间的抗侧滚扭杆和止挡作用，金属止档的刚度应固定为1×108N/m，在止挡发生作用前的刚度应设置在0.5 mm的范围内采用抛物线过渡。对于作用于车体的气动力。不考虑气动阻力作用，计算如下：

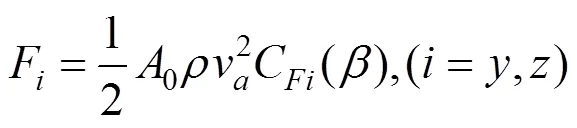
根据图2中的合成速度图，合成风速可以由风速、车速、风向与线路夹角计算得到。合成风速和侧滑角计算公式如下：

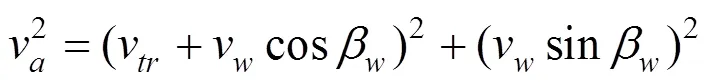
考虑系统中所有质量体的11个自由度，设定车辆系统各刚体的位置矢量，有：

计算各个体上的力和力矩可以构建如下关于车体和转向架力和力矩的系统平衡方程(轮对自由度为0)：

五质量模型的具体数学表达式推导参见文献[11]。EN14067-6中规定应检验五质量方法的计算结果，应做检验，与标准附录中列出的示例车辆的临界倾覆风速曲线的计算进行对照，计算风向角为90°时得到的结果相对于示例车辆最大偏差应在±0.5 m/s内。本文中的计算方法与标准附录算例进行对比后，结果符合要求。

3 列车临界倾覆风速曲线

利用五质量模型方法对车辆进行倾覆计算，得到了不同风速、不同运行速度和不同风向角下高速列车的倾覆系数。为防止车辆倾覆，借助高速列车运行安全性标准，在EN-14067.6中规定倾覆系数D ＜0.9时车辆安全，以0.9作为临界值从而确定临界倾覆风速曲线。

图5 临界倾覆风速随车速变化曲线

图6 车速为200 km/h时临界倾覆风速随风向角变化曲线

图5是风向角为90°时不同未被平衡横向加速度下(a=0，a=0.5 m/s2,a=1 m/s2)列车临界倾覆风速随车速变化曲线。可以看出随着车速增加临界倾覆风速下降，在车速在80~100 km/h之间，CWC值迅速下降，而当速度大于100 km/h 时，CWC下降速度减慢。且在未被平衡横向加速度方向为正时，随着其增大，列车临界运行安全速度减小，不同未被平衡横向加速度下CWC曲线变化规律相同。图6是车速为200 km/h时列车临界倾覆风速随着风向角变化曲线，可以看出CWC曲线最小值出现时的风向角并不是垂直于列车运行方向，而是在=80°。原因是由于侧风作用下列车所受气动系数的特性，对车辆倾覆影响最大的是侧向力和倾覆力矩，而其系数的最大数值点不是在90°时出现，当列车以200 km/h运行时，随着风向角增大，相对于列车的偏航角也增大，但临界角度对应的系数 减小。

4 不同参数对列车倾覆特性影响

4.1 点头力矩和摇头力矩影响

在运用较多的详细解析式法和三质量模型方法中，考虑造成列车倾覆的气动力和力矩时，只考虑了侧向力、升力和倾覆力矩，由于静态模型不考虑列车运行，运行方向的阻力不被考虑。而在五质量模型方法中，不仅考虑了这3个力和力矩，点头和摇头力矩也同时被考虑。因此对比分析了点头力矩和摇头力矩对临界倾覆风速曲线的影响。

图7是不考虑点头或摇头力矩时临界风速变化对比。可以看出，不考虑摇头力矩时，临界风速值变化不大。在车速小于200 km/h时，该条件下临界风速小于正常考虑力矩，车速大于200 km/h时，该条件下临界风速稍大于考虑全力矩时，但相差很小。不考虑点头力矩时，临界风速值变化较大，在车速小于100 km/h时，该条件下临界风速稍小于考虑全力矩时，车速大于100 km/h时，该条件下临界风速大于正常考虑力矩情况，且相差最大值达2.2 m/s。当点头力矩和摇头力矩均不考虑时，临界倾覆风速与正常考虑力矩时相差最大值达2.5 m/s。总体来说是否考虑摇头力矩对临界倾覆风速曲线影响很小，而车速较高时，点头力矩对临界倾覆风速曲线有一定影响。说明详细解析式法或三质量模型方法中不考虑摇头力矩的作用有一定合理性。但考虑点头力矩更合理。不考虑点头力矩时临界倾覆风速较高，对车辆运行安全有不利影响。

4.2 车辆参数影响

车辆结构参数尤其悬挂参数对列车动力学性能有重要影响，尤其是在侧风下运行的列车，车辆产生大幅振动，合适的车体参数能很好的防止列车偏移，保证列车运行安全性。一系悬挂系统能实现轮对的弹性定位，二系悬挂系统能提高转向架平稳性且抑制蛇形运动。因此优化车辆动力学性能，需要考虑各车辆结构参数对其动力学性能的影响。改变某个参数并保持其他参数不变，分析不同车体参数对车辆系统动力学性能的影响。

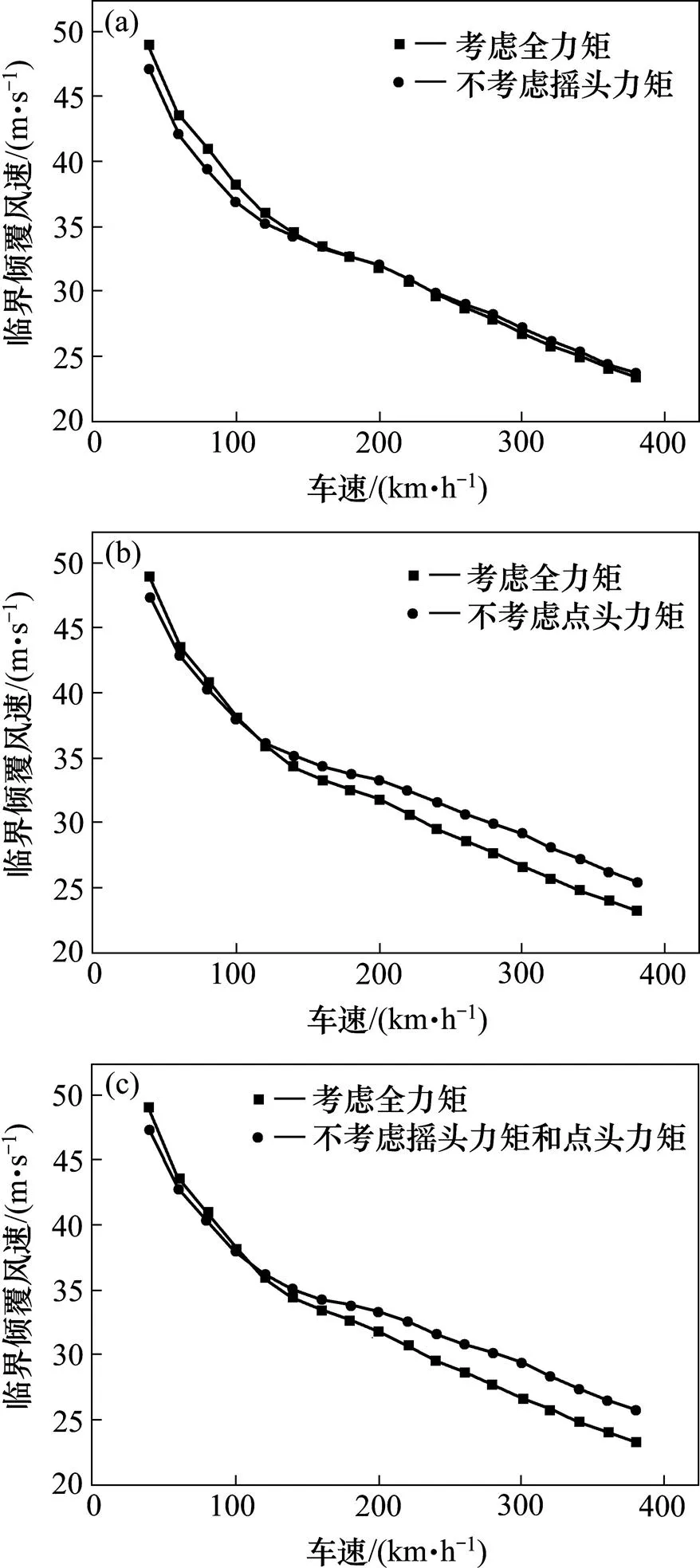
(a) 不考虑摇头力矩；(b) 不考虑点头力矩；(c) 不考虑摇头力矩和点头力矩

由于有些车辆参数的变化对临界倾覆风速的影响不明显，因此以判别车辆临界状态的倾覆系数作为目标结果。考虑五质量车辆模型中的关键特征参数，选定了7个车辆参数进行分析，分别是：一系垂向/横向刚度、二系垂向/横向刚度、二系横向止挡间隙、抗侧滚扭杆刚度、及车辆偏心。由于各参数的量纲差异，为统一比较其对车辆倾覆系数的影响程度，使指标值的变化具有可对比性，在分析过程中将车辆各原参数作为比较基准，以参数变化率为横坐标分析变化情况。设定各参数在原值上增减90%，每隔10%取一个值，其中车辆偏心值过大不符合实际情况，因此考虑车辆偏心范围在±1 m以内。由于环境风速和列车速度工况较多，取车速为200 km/h，风速取25 m/s，未被平衡横向加速度为0，风向角为90°时，计算车辆参数变化对倾覆系数的影响。在五质量模型中，前后转向架轮对的倾覆系数被分开考虑，以较大的倾覆系数值作为倾覆判断值。

图8分别为不同车辆参数变化对车辆倾覆系数的影响。可以看出风速为25 m/s时，由于此时合速度作用下的摇头力矩对车辆影响较大，因此原车辆参数下所计算的列车前转向架轮对倾覆系数比后倾覆系数大，且约高出0.1左右，也说明以单个转向架的倾覆系数作为判别指标的合理性。可以看出一系悬挂参数变化对倾覆系数无明显影响，其中一系横向刚度在其减小量大于70%时倾覆系数略有增大。二系悬挂参数中二系横向刚度减小对倾覆系数的影响很小，其增大时后转向架轮对倾覆系数稍有减小。二系垂向刚度影响较大，随着二系垂向刚度的减小，前转向架轮对倾覆系数增大，后转向架轮对倾覆系数减小，且参数减小到60%时，变化曲线斜率绝对值增大。横向止档自由间隙变化对倾覆系数有一定影响，随着间隙增大前后转向架轮对倾覆系数均增大，当间隙大于原值时，后转向架轮对倾覆系数变化不大。抗侧滚扭杆刚度变化的影响不大，在抗侧滚扭杆刚度减小到原值的60%以上时倾覆系数略有增大，增幅不超过10%。另外车辆偏心对车辆倾覆系数有较大影响，变化率为正时表示车辆质心偏向车辆前端，随着车辆越向前端偏心，前转向架轮对的倾覆系数增加，后转向架轮对的倾覆系数减小。

(a) 一系横向刚度；(b) 一系垂向刚度；(c) 二系横向刚度；(d) 二系垂向刚度； (e) 横向止档间隙；(f) 抗侧滚扭杆刚度；(g) 车辆偏心

5 结论

1) 临界倾覆风速随着车速增加而减小，且随着横向加速度的增大而减小，但曲线变化规律相同。随着风向角的增大(0°~90°)临界倾覆风速先增大后略有减小，曲线最小值出现在风向角为80°左右。

2) 五质量模型算法较为全面的考虑了静态车辆计算所需的气动力，增加考虑了点头和摇头力矩的影响。若不考虑摇头力矩，当车速小于200 km/h时，临界风速小于考虑全力矩时，车速大于200 km/h时，该条件下临界风速变大。点头力矩对临界倾覆风速影响较大，在车速小于100 km/h时，该条件下临界风速稍小于考虑全力矩时，车速大于100 km/h时，该条件下临界风速变大，且相差最大值约达 2.2 m/s。

3) 通过五质量模型算法计算了不同车辆参数对车辆倾覆系数的影响。一系刚度和二系横向刚度对倾覆系数影响较小。随着二系垂向刚度增加，前转向架倾覆系数减小，后转向架倾覆系数增大。随着二系横向止档间隙增大前后转向架倾覆系数均增大。抗侧滚扭杆影响较小，当其减小到原值的60%以上时倾覆系数略有增大，幅度变化不超过10%。若车辆偏心时质心越偏向车辆前端，前转向架倾覆系数随之增加，后转向架倾覆系数减小。说明在计算列车临界倾覆风速时，应重点分析二系垂向刚度、横向止挡间隙和车辆偏心等因素的影响。

[1] 高广军, 田红旗, 姚松, 等. 兰新线强横风对车辆倾覆稳定性的影响[J]. 铁道学报, 2004(4): 36−40. GAO Guangjun, TIAN Hongqi, YAO Song, et al. Effect of strong cross-wind on the stability of trains running on the Lanzhou-Xinjiang railway line[J]. Journal of the China Railway Society, 2004(4): 36−40.

[2] 刘加利, 于梦阁, 张继业, 等. 基于大涡模拟的高速列车横风运行安全性研究[J]. 铁道学报, 2011, 33(4): 13−21. LIU Jiali, YU Mengge, ZHANG Weihua, et al. Study on running safety of high-speed train under crosswind by large eddy simulation[J]. Journal of the China Railway Society, 2011, 33(4): 13−21.

[3] Andersson E, Haggstrom J, Sima M, et al. Assessment of train-overturning risk due to strong cross-winds[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2004, 218(3): 213−223.

[4] 葛盛昌. 新疆铁路风区大风天气列车安全运行办法研究[J]. 铁道运输与经济, 2009, 31(8): 32−34, 84. GE Shengchang. Study on train safety operation method in the Xinjiang railway under cross wind[J]. Railway Transport and Economy, 2009, 31(8): 32−34, 84.

[5] Kunieda M, Theoretical study on the mechanics of overturn of railway rolling stock[R]. Railway Technical Research Report, 1972(793): 1−15.

[6] 日比野有, 石田弘明.車両の転覆限界に関する静解析式法[J].鉄道総研報告, 2003, 17(4): 39−44. Hibino Tamotsu, Ishida Hiroaki. On the static analysis method for the limit of covering[J]. Report of Railway, 2003, 17(4): 39−44.

[7] Thomas D, Diedrichs B, Berg M, et al. Dynamics of a high-speed rail vehicle negotiating curves at unsteady crosswind[J]. Journal of Rail and Rapid Transit, 2010(224): 567−579.

[8] Baker C J. The wind tunnel determination of crosswind forces and moments on a high speed train[M]. Berlin: Springer- Verlag Berlin Heidelberg, 2002.

[9] Baker C J. The behaviour of road vehicles in unsteady cross winds[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1993(49): 439−448.

[10] Baker C J. Ground vehicles in high crosswinds parts I: Steady aerodynamic forces[J]. Journal of Fluids and Structures, 1991(5): 69−90.

[11] EN 14067-6: 2010, Railway applications-aerodynamics- part 6: Requirements and test procedures for cross wind assessment[S].

[12] 王福军. 计算流体动力学分析[M]. 北京: 清华大学出版社, 2004: 210−215. WANG Fujun. Analysis of computational fluid dynamics [M]. Beijing: Tsinghua University Press, 2004: 210−215.

Study on critical overturning wind speed of high-speed train under cross wind

LIU Rong1, 2, 3, YAO Song1, 2, 3, XU Jiaoe1, 2, 3

(1. Key Laboratory of Traffic Safety on Track, Central South University, Ministry of Education, Changsha 410075, China;2. Joint International Research Laboratory of Key Technology for Rail Traffic Safety, Changsha 410075, China; 3. National & Local Joint Engineering Research Center of Safety Technology for Rail Vehicle, Changsha 410075, China)

The aerodynamic coefficients of high-speed train under crosswind were calculated by numerical simulation method. The five-mass model of EN14067 was used to study the critical overturning wind speed curve of vehicles under crosswind and the influence of different parameters on its overturning. Results show that: the critical overturning wind speed decreases with the increase of vehicle speed, critical overturning wind speed first decreases and then increases with the increase of wind direction angle, and the minimum value appears at about 80°, and decreases with the increase of unbalanced lateral acceleration. The shaking moment and nodding moment have a certain impact on the critical overturning wind speed, If the nodding moment is not taken into account, the critical wind speed limit of the vehicle will be set higher, which has a negative impact on the safety of the train operation. The primary suspension parameters and the second lateral stiffness have little effect on the overturning coefficient. With the increase of the vertical stiffness of the secondary system, the overturning coefficient of the front bogie wheel set decreases and that of the rear bogie increases. With the increase of lateral stop clearance both overturning coefficients increase. When the anti-roll torsion bar is reduced to more than 60% of the original value, the overturning coefficient increases slightly, and the range is not more than 10%. When the centroid of the vehicle leans towards the front end of the vehicle, the overturning coefficient of the front bogie wheel set increases and the overturning coefficient of the rear bogie wheel set decreases.

high-speed train; crosswind environment; five-mass model; critical overturning wind speed

U271.1

A

1672 − 7029(2019)11− 2643 − 08

10.19713/j.cnki.43−1423/u.2019.11.001

2019−02−26

国家重点研发计划资助项目(2016YFB1200506-03)

姚松(1975−)，男，湖北公安人，教授，博士，从事轨道交通安全研究；E−mail：song_yao@csu.edu.cn

(编辑 蒋学东)