EasiFFRA:一种基于邻域粗糙集的属性快速约简算法
2019-12-18彭政红
王 念 彭政红 崔 莉
1(中国科学院计算技术研究所 北京 100190)2(中国科学院大学 北京 100190)(wangnian@ict.ac.cn)
在物联网应用场景中,系统通常需要部署大量感知节点来获取环境信息.为充分利用每个节点的传感信息以支持后续精准的识别与预测,实际应用中系统通常会从每个节点的原始信息中提取大量特征,并通过串行融合[1]的方式对数据集进行特征级多源信息融合,形成超级特征(super feature),并进行后续的机器学习模型训练和验证操作.但在每个传感器的大量特征中,通常包含了与决策任务无关、弱相关或相互冗余的特征.此类特征不但对于决策结果无明显贡献,而且会增加计算量,从而降低决策效率,进而影响后续分类或预测操作的性能.若可找出并去除此类特征,则可提高系统实时性并减少所需传感器的种类及数量.因此在特征工程中,有必要在决策前对原始数据进行降维操作.
目前常用的降维方法包括线性方法、相关性分析法、主成分分析法和基于邻域粗糙集的特征约简方法等[2].其中,线性方法无法适用于非线性场景;相关性分析和主成份分析法会造成原属性集中部分信息丢失;而基于粗糙集的方法能够在无任何先验知识(如统计中的先验概隶属度等)的情况下,保留数据集的基本知识和分类能力,并消除重复和冗余的特征,是一种有效的特征约简算法.然而目前已有的基于邻域粗糙集的特征约简算法[3-5]中存在较多冗余计算,严重限制了算法的执行效率.约简效率会影响算法的整体实时性,尤其对于在线学习以及数据有较强时效性的场景中,频繁或定期的模型重构会要求较高的特征约简速度.针对上述问题,本文提出了一种基于邻域关系对称性及决策值过滤策略的特征快速约简算法(Easi fast Hash feature reduction algorithm,EasiFFRA).
1 相关工作与背景知识
1.1 背景知识
粗糙集理论是Pawlak[6]提出的一种定量分析处理不精确、不一致和不完整信息的方法.目前该理论已被广泛应用于人工智能、模式识别和数据挖掘等领域[7-10].但作为一种有效的粒度计算模型,粗糙集理论只适用于名义型数据,无法直接应用于现实中广泛存在的连续型数据.为处理连续性数据,研究人员往往需要对连续型数据进行离散化,但这一转换不可避免地带来了信息损失,且计算结果受到了离散化的影响.为解决这一问题,胡清华等人[3]基于拓扑空间球形邻域提出了邻域粗糙集(neighborhood rough set,NRS)理论.其核心是使用邻域近似代替经典粗糙集中的等价关系,以使其既支持离散型数据又支持连续型数据.邻域粗糙集有效拓展了粗糙集的应用范围,使其在特征约简、模式识别等方面有着长足的发展[11-14].
1.2 相关工作
特征约简是邻域粗糙集最重要的也是核心内容之一[4,8,15-16].通常,系统的特征相对约简结果不唯一,人们期望找到一种具有最少特征维度的约简方法,即最小约简.但寻找最小约简已被证明是一种NP难问题[17],故而研究者们主要致力于用高效的约简算法找到一个较优的属性子集[4-5,16,18].胡清华等人[3,5]利用正域与属性集的单调关系提出了基于前向贪心启发式搜索策略(fast forward heterogeneous attribute reduction based on neighborhood rough sets,F2HARNRS)算法,该算法从空集开始构建约简集合,每一次迭代过程都将当前特征集合中具有最大正域值的属性加入约简集合,并过滤掉论域中已经属于正域的样本.虽然通过去除正域样本缩小了搜索空间,但整个约简算法时间复杂度仍为O(m||U|2),其中m为属性个数,|U|为样本总个数,并且算法效率会受到数据分布情况的影响.为解决F2HARNRS算法邻域计算的时间复杂度过高的问题,Liu等人[4]在文献[3,5]的基础上提出了基于散列划分桶缩小邻域搜索空间的属性快速约简算法(fast Hash attribute reduct algorithm,FHARA).该方法根据给定的邻域决策系统NDS=〈U,C∪D,V,f〉及距离度量δ,利用散列映射将论域U中的样本划分到有限集合B0,B1,…,Bb中.样本划分情况如图1所示:
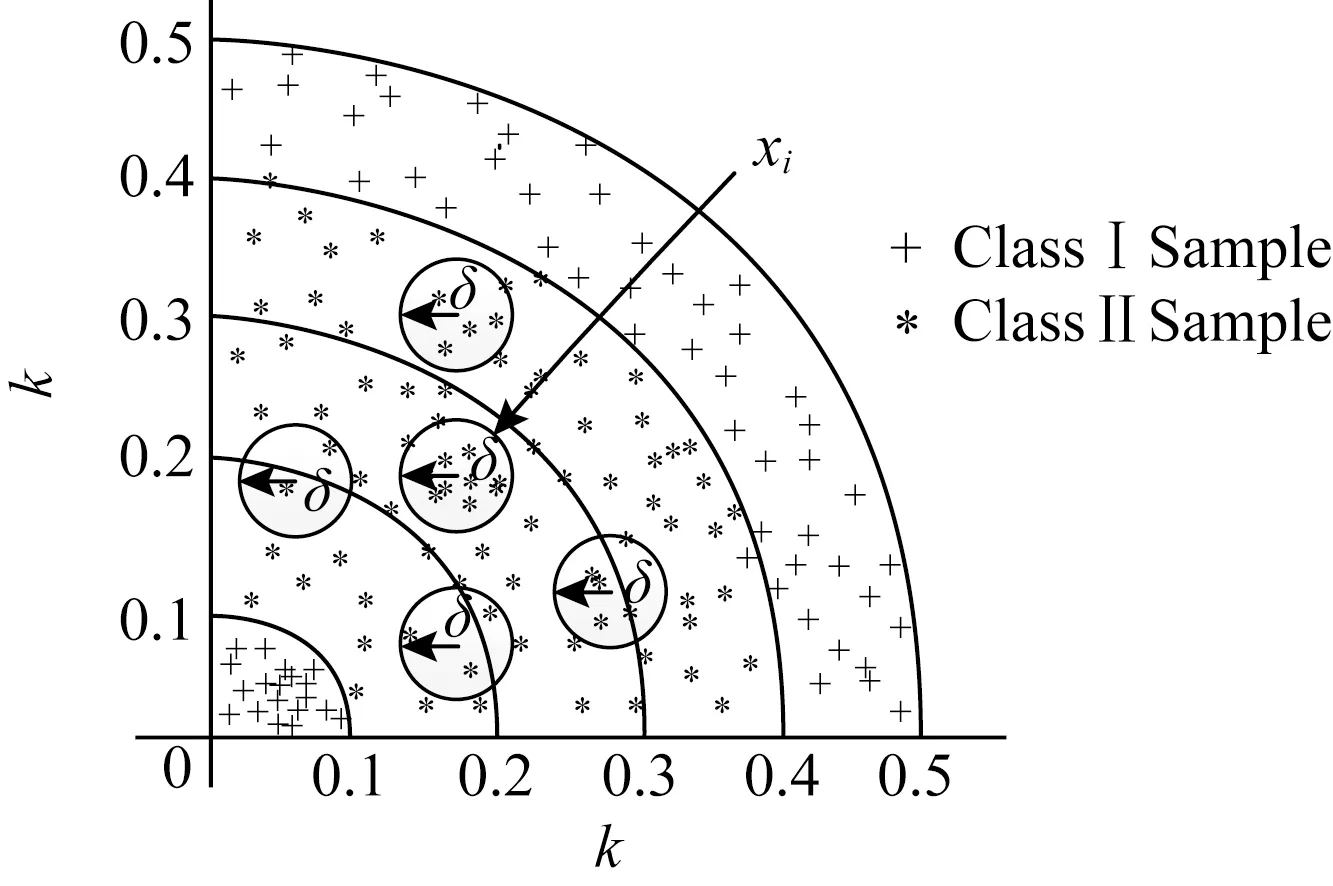
Fig.1 The distribution of the buckets图1 桶划分示意图
映射函数为Bk={xi|xi∈U∧┌f(x0,x1)/δ┐=k},其中x0是由每个属性的最小值组成的一个特殊样本.以k作为散列键[4]组成的数据桶的空间分布类似由多个大小不等的球嵌套而成的组合体,散列键k为映射后球的半径.样本分布在球面与球面之间,B0,B1,…,Bn就是以k作为半径所得的n个数据桶.经过桶划分策略进行样本空间映射后,集合中的每个样本的邻域搜索范围由原来的整个样本空间减小到相邻的3个数据桶,与F2HARNRS算法相比,FHARA明显降低了样本邻域的搜索范围,降低了算法的计算复杂度.
如图1所示,在计算某个样本xi的邻域时,只需考虑xi所在桶以及相邻2个桶内的样本.Liu等人[4]提出的散列分桶策略缩小了邻域样本存在的可能范围,使得整个约简算法时间复杂度下降为O(m|U|2/k),其中k为桶的个数.然而,分析发现每个桶中依然存在大量不属于xi邻域的样本,这意味着FHARA在计算样本的邻域时仍然存在很多冗余计算.以表1中的样例数据为例,其中a,b,c,d为条件属性,即特征(feature);e为决策属性,即标签(label).当δ=0.1时,则有x0={0.17,0.11,0.27,0.33},样本的桶划分情况为:B0={x7},B1={x1,x2,x3,x6},B2={x4},B3={x5,x8}.FHARA首先计算B0中样本x7的邻域.由桶划分机制可知,在计算B0中样本的邻域时只需遍历B1即可.记xi与xj之间的距离为D(xi,xj),则D(x7,x1)=0.152,D(x7,x2)=0.148,D(x7,x3)=0.19,D(x7,x6)=0.093.当计算出x7与x1的距离D(x7,x1)大于邻域半径δ时,系统可推断x1不在邻域范围内.同理,x2,x3也不在邻域范围内.计算x7与x6的距离,发现D(x7,x6)小于邻域半径,但两者拥有不同的决策值,可知x7为边界区样本;至此,B0中样本的邻域计算完毕.计算B1中样本的邻域,需要遍历B0∪B1∪B2桶.首先计算样本x1与x7的距离D(x1,x7).而D(x1,x7)与D(x7,x1)等价,故而没有必要重复计算.可以看出,FHARA的邻域计算过程中存在冗余计算.
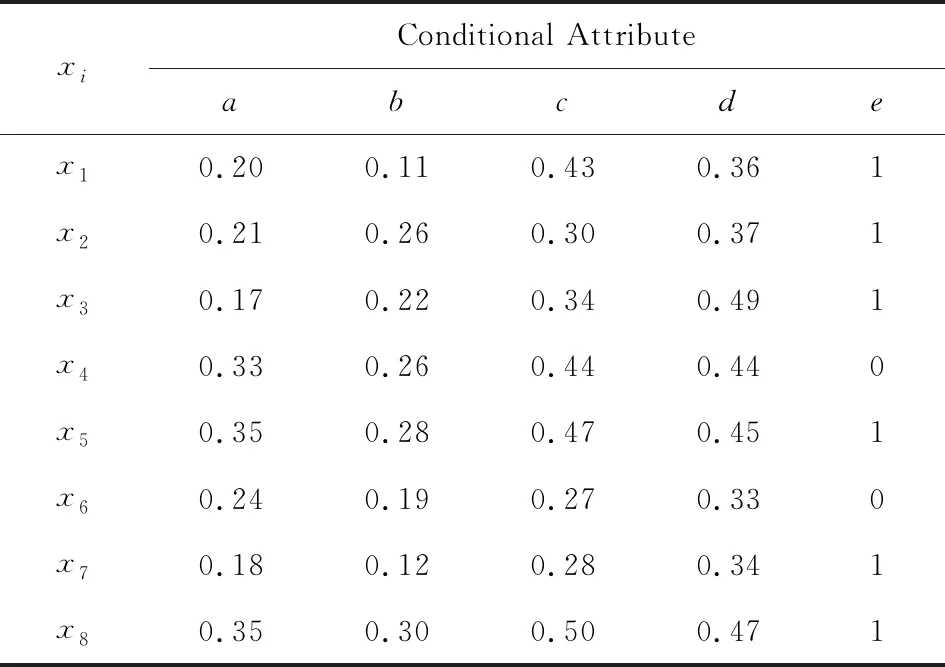
Table 1 An Example Dataset表1 样例数据
蒋云良等人[19]在文献[3-5]的基础上,采用迭代的方式求解样本邻域,即在每次迭代过程中只搜索Bk和Bk+1两个桶,避免了FHARA中相邻桶内样本邻域关系的重复计算问题.但是该算法须计算Bk与Bk+1之间的完整邻域关系,以便在下一次迭代过程中避免搜索Bk-1桶(即当前迭代中的Bk桶).故而当邻域样本分布在相邻的多个桶中时,该算法的邻域计算量较大.
文献[3,5,19]均可利用邻域粗糙集理论实现特征约简.其中文献[3,5]初步建立了特征约简的思路,即迭代贪心搜索并保留具有最大正域值的属性;文献[4]发现贪心搜索中正域计算时的邻域搜索空间的遍历具有盲目性,于是针对此提出了基于散列划分桶的方法.该方法可以缩小邻域搜索空间并避免部分冗余计算;文献[19]也基于文献[3,5]的算法框架,约束了正域计算过程中桶搜索的范围,避免相邻桶内样本邻域关系的重复计算问题,从而进一步提高了邻域粗糙集特征约简的效率.但现有的特征约简算法中仍存在冗余计算.
针对当前已有方法中存在的邻域冗余计算问题和邻域计算量过大的问题,本文提出基于邻域对称性及决策值过滤策略的属性快速约简算法(EasiFFRA),并在太湖实际采集的水质监测数据集合,以及多个UCI(University of California Irvine)国际标准数据集上进行实验,以验证本方法的有效性.本文的主要贡献体现在3个方面:
1)通过散列表存储邻域计算过程中被判定为边界区的样本,减少了邻域计算过程中的冗余计算量;
2)采用优先搜索样本所在桶的策略,提前发现邻域样本,从而加速正域的计算;
3)采用决策值过滤策略,减少了邻域距离的计算次数,从而大幅降低算法的计算量;
对比实验表明:EasiFFRA在同等约束条件下有较大优势,可以在保持约简结果的情况下加快特征约简的速度.
2 邻域粗糙集属性约简机制
在已有的基于邻域粗糙集的特征约简步骤中,算法通常需要遍历并保留能够引起最大正域样本增量的特征,直到增加其他特征也无法引起正域集合的扩大,算法停止.在该类约简过程中,算法需要对所有未保留的特征进行遍历,并计算每种组合下的正域样本集合.此过程是算法中计算量最大的步骤,存在计算冗余.本节介绍在文献[4]的基础上所提出的基于邻域对称性和决策值过滤策略的EasiFFRA特征快速约简算法.
2.1 基于邻域对称性的约简机制
邻域具有对称性[3],该性质可用于避免大量现有工作中的冗余正域计算操作即在度量空间和δ邻域中,有:
δ(xi)≠∅,∀xi∈δ(xi),
(1)
xj∈δ(xi)⟹xi∈δ(xj),
(2)
(3)
也就是说,如果xi是xj的邻域样本,那么xj也是xi的邻域样本,如图2所示:
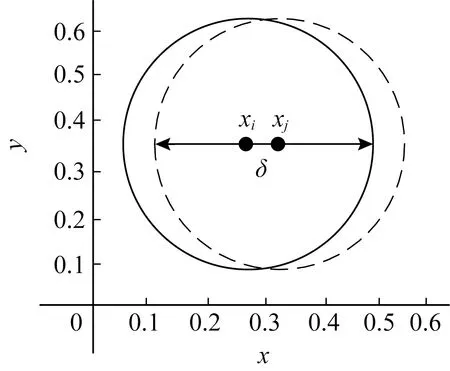
Fig.2 Neighborhood symmetry图2 邻域对称性示意图
在邻域粗糙集理论中,数据集合可以分为3个区间,即A类样本正域、B类样本正域和边界区.其中正域样本是在数据集中可以根据其自身特征分布明确分类的样本;而边界区的样本则是无法十分明确归类的样本,即存在一定的混淆.在判断某样本xi是否为正域元素的过程中,需要遍历xi邻域范围内的所有样本的标签值.若在xi邻域范围内存在与其标签值不同的样本,则xi为边界区样本;若xi邻域内所有的样本均与其标签值相同,则xi为正域样本.
不同类别样本正域和边界区中样本的并集即为整个数据集.边界区数据集合和正域中数据集合不相交.
根据正域的定义及其计算规则,在同一属性子集条件下计算样本xi的邻域时,如果xj在xi的邻域范围之内,且xj与xi的决策属性不同(不属于同一类别),则xi不可能属于正域集合.同理,由于对称性xj也不可能属于正域集合.根据这一特性,通过一个散列表Hs来存储尚未计算过邻域但已经判定为边界区的样本子集.比如若判定xj导致xi为边界区样本,则将xj存入散列表Hs,在后序判断xj是否为正域样本时,将首先检索散列表Hs中是否存在xj的记录,如果存在则无需检索任何桶中的样本,可直接将xj判别为边界区样本,从而避免了大量冗余的邻域计算.
由散列分桶映射函数可知,散列桶划分策略使得距离相近的样本以更大概率被划分到同一个桶中,即样本xi(xi∈Bk)的邻域样本出现Bk中的概率大于出现在Bk+1和Bk-1桶的概率.这也意味着Bk桶内出现由xi导致的边界区样本的概率大于Bk+1,Bk-1中出现由xi导致的边界区样本的概率.所以在改进算法中,优先检索Bk桶.又因为Bk-1中的非邻域样本在上一轮迭代过程中已经存储在散列表Hs中,无需再次检验存储,所以可以在检索Bk后直接检索Bk+1桶.基于上述桶检索顺序,并结合邻域的对称性,可以尽早的发现尽可能多的边界区样本,减少不必要的检索计算.在后续的实验部分中将对其进行进一步的论述与验证.
2.2 基于决策值过滤策略的约简机制
在已有邻域粗糙集特征约简算法的正域计算步骤中,当判断样本xi是否处于正域时,需遍历样本集中所有其他数据xj,并计算xi与所有xj之间的距离,而不论xj和xi的决策属性类别是否相同、是否处于同一个邻域内.这种朴素的计算方法中存在若干冗余计算:
在样本xi正域的求解过程中,若其δ邻域中存在一个决策属性不同的样本,则xi将被判别为边界区样本.只有当xi的δ邻域中所有样本都与其决策属性相同时,xi才会被划分为正域样本.故而可以将朴素的遍历过程简化为仅关注xi的δ正域内是否存在异类决策属性的样本即可.
在本文提出的算法中,仅遍历与样本xi决策属性类别不同的样本子集,计算并考察该样本子集中各样本点xj与xi间的距离D(xi,xj),此时有2种情况:
1)若D(xi,xj)>δ,则xj不会对xi的正域判别产生影响;
2)若D(xi,xj)<δ,则由于xj的影响,xi将无法被归类为正域元素,并被划分入边界区.
综上,在判断xi是否为正域样本时,只需考虑与xi决策属性不同的样本子集.该集合中与xi决策属性相同的样本不会对xi的正域属性判断产生影响,可以直接忽略,此方法即为决策值过滤策略.
例如在表1的样例数据中,可以首先比较x7与x1,x2,x3的决策属性,发现决策属性均相等,便可直接省去x7与x1,x2,x3间的距离计算.虽然决策值过滤策略并未降低算法的时间复杂度,但是可以减少大量样本间的距离计算,使得整个约简算法的计算开销大幅下降,正域的求解效率也就得以提高.
实验表明:对于决策属性取值情况较少的数据集,尤其是二分类的情况,通过决策值过滤策略带来的计算效率提升十分明显.
2.3 属性约简改进算法
结合邻域对称性和决策值过滤机制,下面给出正域求解算法的伪码,如算法1所示.
算法1.基于对称及决策过滤的快速约简算法.
输入:U,P,D,δ;
输出:F={F1,F2,…,F|U|}.
①Fi←0,1,…,|U|;
② for eachxi∈Udo
③ Hash(P(xi),Bk);
④ end for
⑤ for eachxi∈Udo
⑥flag←0;
⑦ ifxi∈Non_Posthen
⑧flag←1;
⑨ else
⑩ for eachxi∈Bk∪Bk+1do
其中,由于Bk-1桶的处理与Bk∪Bk+1类似,唯一区别是无需将Bk-1桶的边界区样本存入散列表Hs(因为这些边界区样本在上一轮迭代过程中已经存入散列表Hs),故而其操作过程在算法中省略.
算法1可判断样本是否为正域样本,其流程如图3所示,其中以xi,xj的单次比较为例.下面结合流程图对算法1进行阐述.
算法1首先判断xi是否存在于记录边界区样本的散列表Hs中,如果存在则说明xi在前面的迭代过程中曾导致其他样本成为边界区样本.根据邻域对称性,xi也不是正域样本,故而被存入散列表Hs中.此时可直接判断xi为边界区样本,并将xi的标志位flag设置为1.其中标志位为记录该样本是否为边界区样本的标志位.
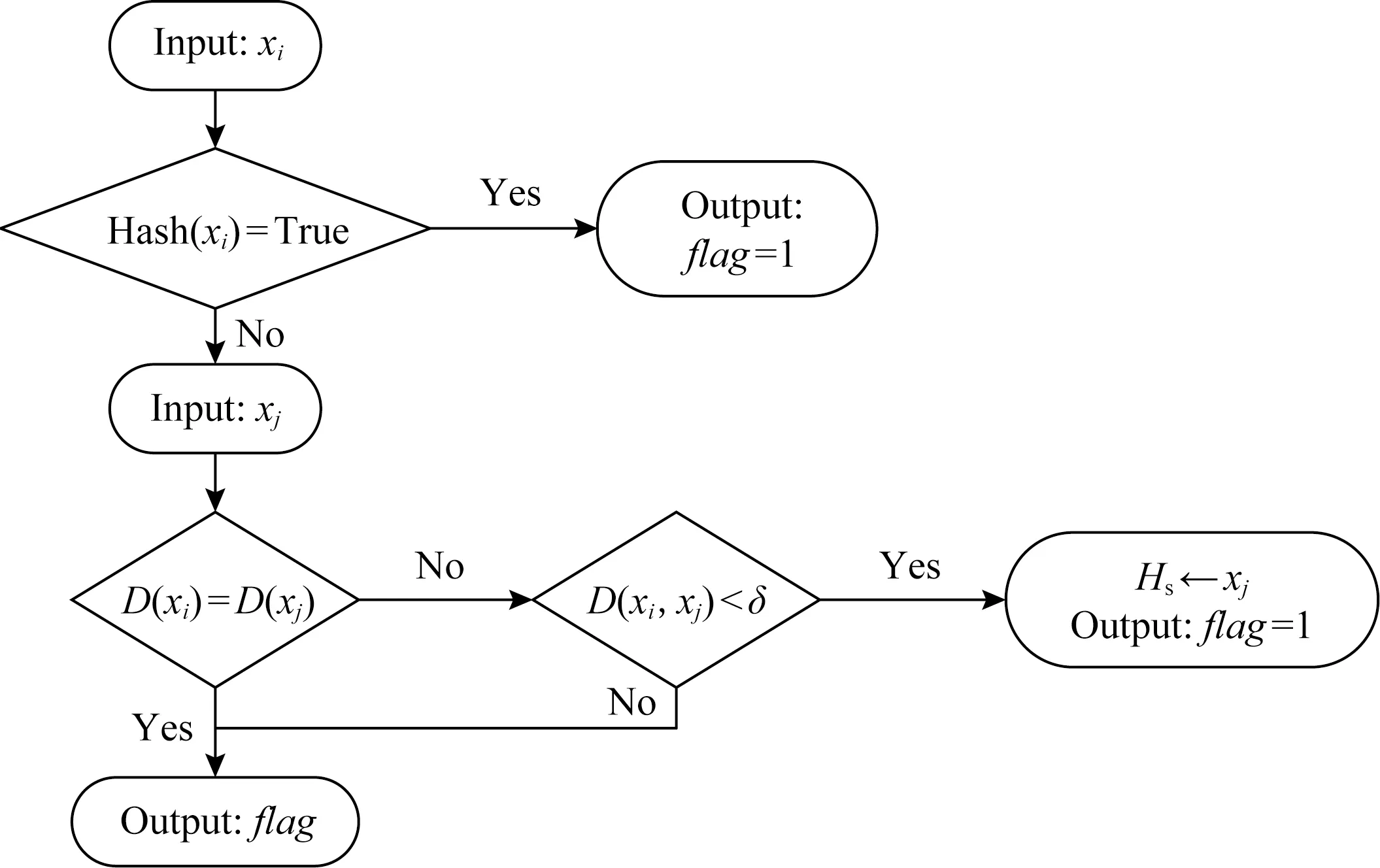
Fig.3 Positive region computation algorithm图3 正域的计算流程图
如果xi不在散列表Hs中则需要检索邻域空间的样本.假设检索到样本xj,首先判断xi和xj的决策值是否相等.如果相等则根据决策值过滤机制可无需继续计算xi和xj之间的距离,可以直接转向其他样本的检索;如果决策值不相等则继续计算邻域距离D(xi,xj);
如果D(xi,xj)>δ,则说明xi不是xj的邻域样本,它对xi是否为正域样本的判断无影响,所以无需修改标志位;如果D(xi,xj)≤δ则说明xi为边界区样本,则将标志位置为1,根据邻域对称性可知,xj也为边界区样本,需将xj存入散列表Hs.
3 实验分析
为了验证本文提出的EasiFFRA算法的正确性与约简的高效性,本节将其与现有方法中特征约简时间效率最高的FHARA方法进行对比实验.实验内容包括算法的正确性验证以及算法的高效性验证.实验数据包括本研究组实际部署与监测的水质监测系统藻类数据集blue green algae[20],以及UCI公开数据集中的12组样本.实验中使用的数据集名称、样本数量、特征维度和决策属性数量信息如表2所示.
实验中,所有算法均选取欧氏距离作为正域计算度量函数,测试运行在相同的软件和硬件环境下CPU为Intel Core i5-4590 CPU@3.30 GHz;RAM为8.00 GB;Windows 7 OS;python 2.7.10.为保证数据的有效性和结果的可重复性,结论中的约简结果以及特征约简速度数据均为10次相同环境下运行结果的平均值.
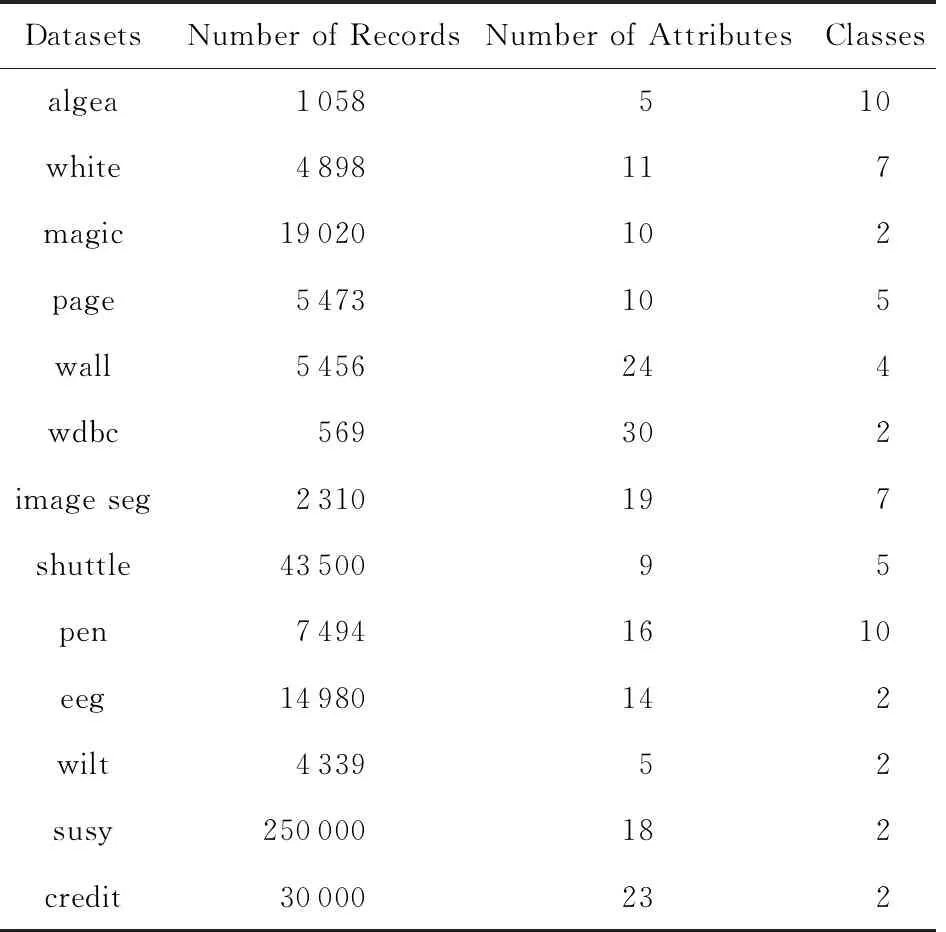
Table 2 Datasets Used in Experiments表2 实验数据集
3.1 算法正确性验证
为验证EasiFFRA算法的正确性,实验同时在algea以及12个UCI数据集上同时执行FHARA算法以及EasiFFRA算法,并比较它们的约简结果.约简结果如表3所示.
从表3可以看到,EasiFFRA和FHARA在所有数据集上的约简结果均相同,又因为文献[4]中FHARA的正确性验证、可验证本文提出的EasiFFRA算法约简结果的一致性与正确性.为进一步验证EasiFFRA约简结果的正确性,实验同时比较经过EasiFFRA约简、经过常用的随机森林特征约简和未经任何约简的数据集的5折交叉分类精度,结果如图4所示.其中使用SVM作为分类器.
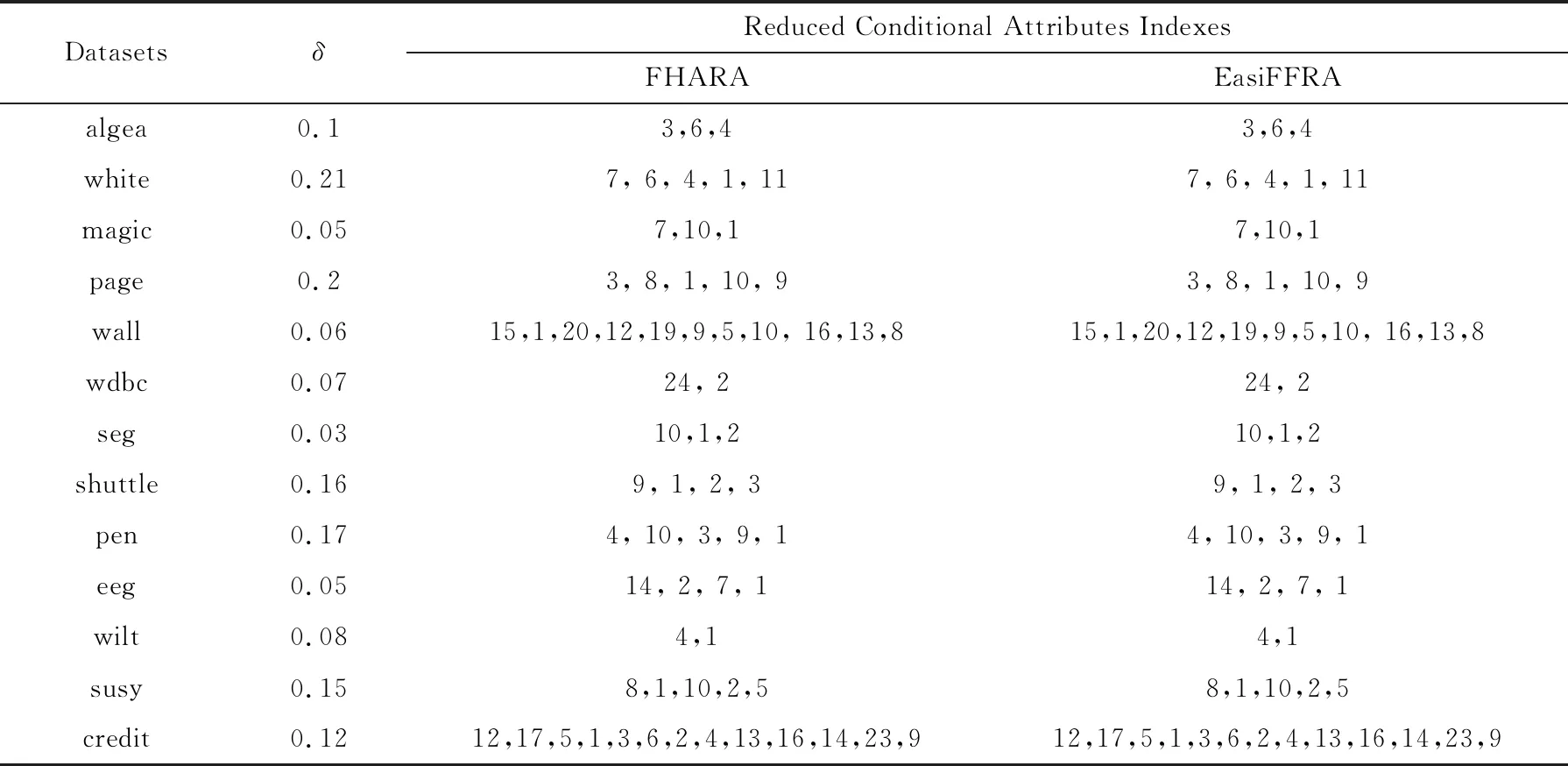
Table 3 Attributes Selected by Two Reduct Algorithms表3 2种算法约简结果
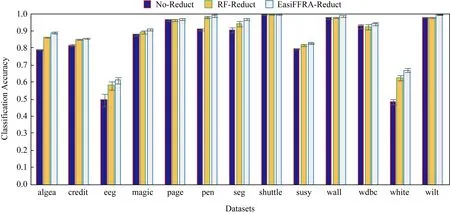
Fig.4 Classification accuracy of SVM in several datasets with EasiFFRA reduction,no-reduction and random forest reduction图4 EasiFFRA与无约简及随机森林约简后各数据集精度对比
从图4可以看到,建立在经过特征约简后的数据集上的分类器的识别精度优于未经约简的原始数据集的精度.而在约简算法中,经过EasiFFRA处理的分类器精度普遍高于传统的随机森林约简算法的结果.这也从另一方面验证了本文提出的EasiFFRA特征约简算法的正确性.
3.2 算法约简效率对比实验
为验证EasiFFRA的特征约简的高效性,实验分别统计EasiFFRA以及对比方法执行过程中的样本间距离计算次数、整体算法运行时间以及算法运行时间随样本数量增加而延长的计算耗时.
1)计算EasiFFRA在不同桶搜索顺序下样本距离的计算总量,以及FHARA在相同数据集下的样本间距离计算次数.如表4所示.
表4表头中EasiFFRA后跟随的3位数字代表EasiFFRA算法在不同桶搜索顺序下的算法,如012代表依次搜索Bk-1,Bk,Bk+1桶.从表4可知,在桶搜索顺序的选择中,优先搜索Bk时的样本距离计算次数与开销最少;对比EasiFFRA与FHARA的距离计算次数可知,EasiFFRA算法在6种桶搜索顺序下的距离计算开销均少于FHARA算法.特别在wilt,magic,credit,shuttle等决策属性种类较少的数据集上的效率提升最多,在seg,pen等决策值种类较多的数据集上计算量也有着明显的降低.以EasiFFRA102的桶搜索顺序为例,EasiFFRA在pen上的距离计算次数小于FHARA距离计算次数的1/3,在seg上的计算次数小于FHARA计算次数的 1/4,在algea上的距离计算次数不到 FHARA 距离计算次数的 1/19.
2)计算EasiFFRA 在相同条件下的算法执行时间.为验证算法的普适性和有效性,按照邻域半径δ将实验分为0.08和0.15这2组.实验结果如图5所示.
为直观展示 EasiFFRA 的约简高效性,实验统计了2种方法的约简计算时间(单位为s),如表5所示.
从表5看到,相对于现有的FHARA方法,不论在δ=0.08还是δ=0.15的情况下,本文提出的EasiFFRA算法在12个验证数据集上均具有更高的约简效率,且对于决策值种类较少的数据集提升更为明显.EasiFFRA在12个数据集上的平均约简时间仅为对比方法FHARA的24.45%.此外,在algae数据集中样本不平衡问题十分严重,其中决策值为0的样本占整体数据量的92.34%,其他9个决策值的样本共占整体数据量的7.66%,可见EasiFFRA在该类决策值种类多且分布不平衡的情况下也能够达到很好的约简性能,验证了其良好的适用性.
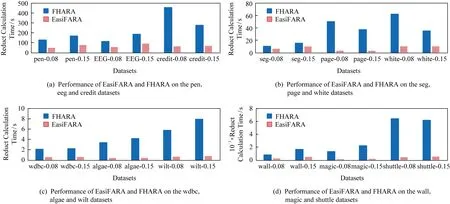
Fig.5 Reduct calculation time cost of FHARA and EasiFFRA on 12 UCI datasets with δ equals 0.08 and 0.15图5 δ=0.08和δ=0.15 时,EasiFARA和FHARA算法在12个UCI数据集上的约简时间

Table 5 Ratio of Reduct Calculation Time Cost of FHARA and EasiFFRA表5 EasiFFRA与FHARA约简时间比
3)实验在保持邻域半径不变的情况下,对比EasiFFRA和FHARA算法在随样本量增加而延长的算法耗时.在本实验中,除了用到的12个数据集外,实验还从UCI数据集中提取了含有250 000个样本的susy数据子集来验证EasiFFRA在大数据集下的性能表现.实验结果如图6和表6~9所示.
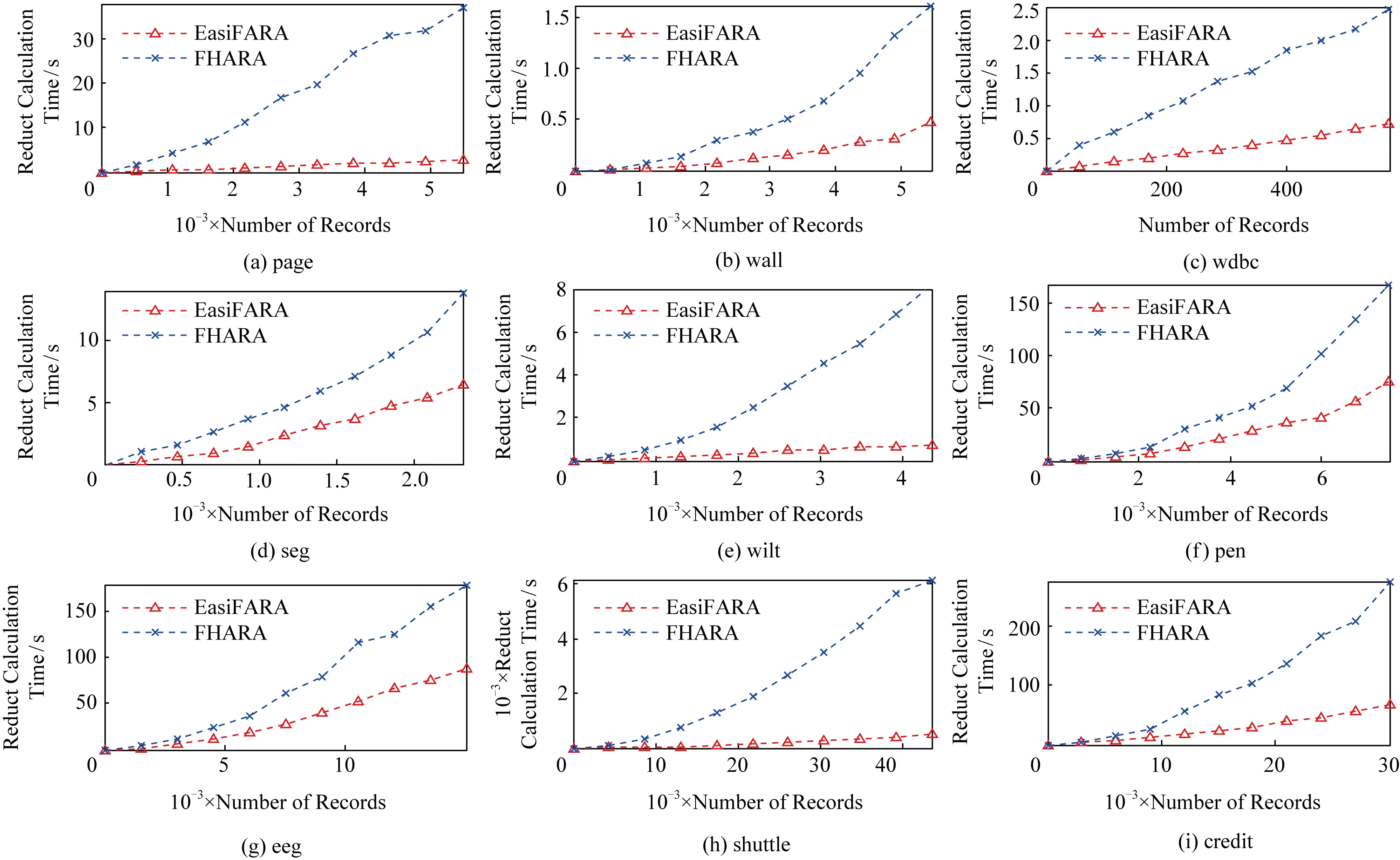
Fig.6 Calculation time cost of EasiFFRA and FHARA on 9 datasets with increasing sample size图6 FHARA和EasiFFRA在9个数据集上随着样本数量的增加所消耗的时间
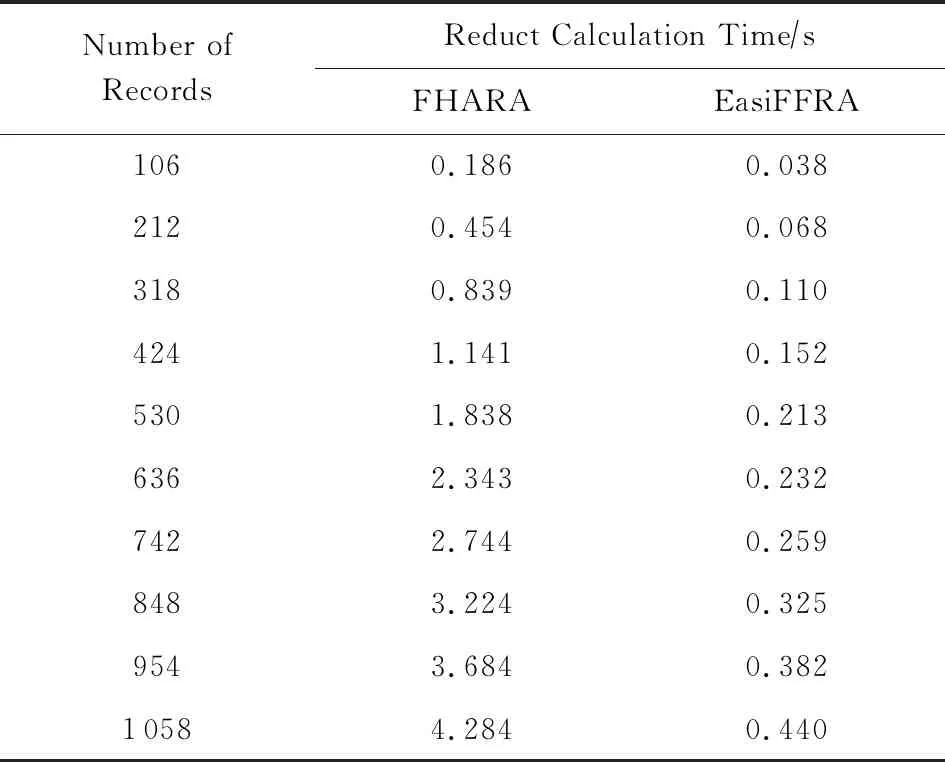
Table 6 Calculation Time Cost of EasiFFRA and FHARA on algae表6 EasiFFRA和FHARA在algae数据集上的约简时间
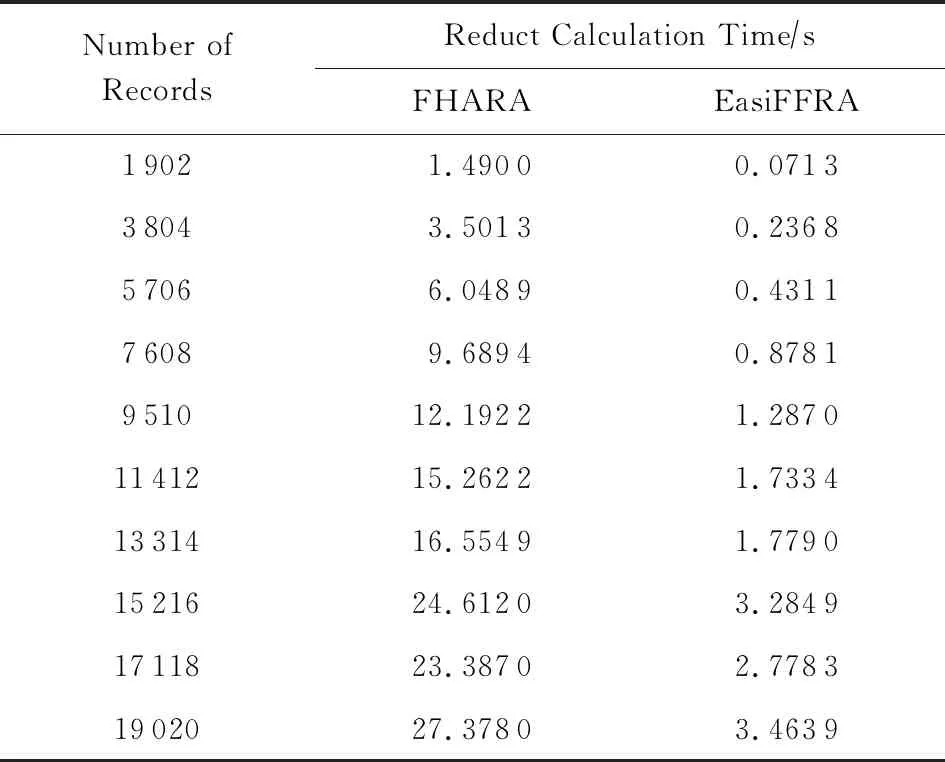
Table 7 Calculation Time Cost of EasiFFRA and FHARA on magic表7 EasiFFRA和FHARA在magic数据集上的约简时间
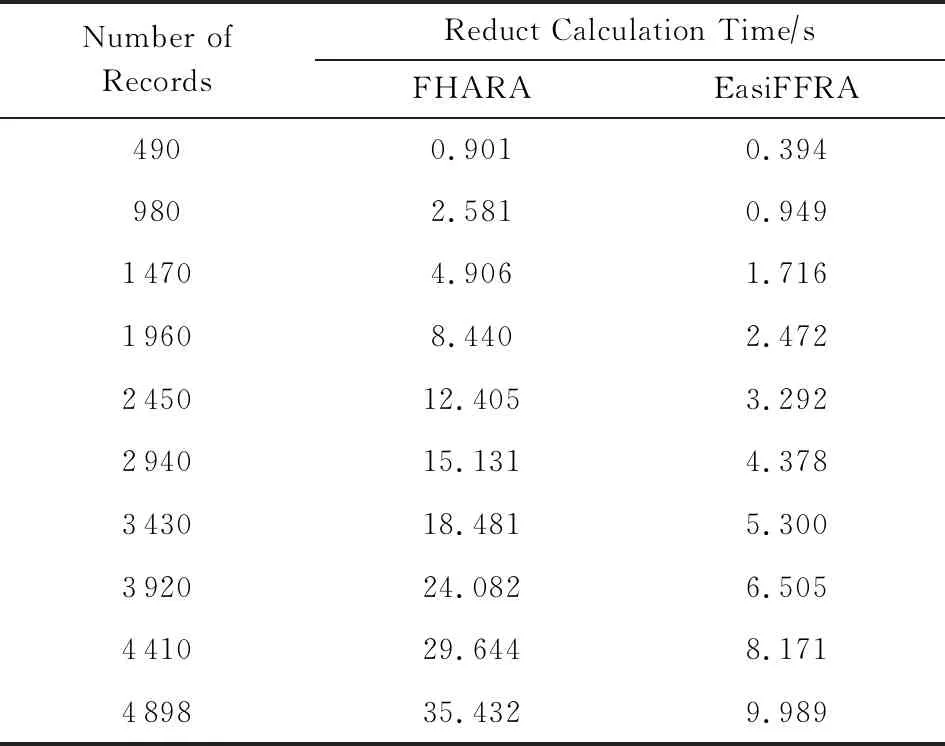
Table 8 Calculation Time Cost of EasiFFRA and FHARA on white表8 EasiFFRA和FHARA在white数据集上的约简时间
从实验结果中可以看到,随着样本量的增加,EasiFFRA在这13个数据集上的约简效率均优于FHARA.尤其在shuttle,susy等决策值种类较少且数据量大的场景下,EasiFFRA的约简耗时明显低于FHARA.上述现象说明EasiFFRA算法能够更好地适用于大数据应用场景.
4 结 论
物联网场景中的大量感知数据的特征具有高维、冗余、非线性等特点.冗余特征和无关特征会导致分类模型准确率下降,也会造成计算资源浪费,因此有必要对数据集进行降维预处理.相对于其他降维算法,邻域粗糙集特征约简算法能够在保持数据可分性的前提下删除无关、弱相关和冗余特征,具有很大的应用优势,但其较大的计算复杂性成为算法实际部署的瓶颈.本文针对邻域计算时间复杂度过高、计算量过大的问题,提出了基于邻域关系对称性及决策值过滤策略的特征约简算法EasiFFRA.该算法优先检索邻域样本分布相对集中的相邻桶Bk,采用散列表存储当前属性子集条件下不可能成为正域样本的方法,缩小邻域检索范围;并通过决策值过滤策略过滤掉与当前样本具有相同决策值的冗余样本,减少了邻域计算时的距离计算次数,从而降低算法的计算量.对比实验表明EasiFFRA避免了大量冗余计算,算法效率明显优于对比方法,能更好地适应复杂的物联网数据分析场景.
