非线性压电耦合对L型梁俘能器性能的影响

马 戈，谢 进，汪 灿，邹 政

(西南交通大学 机械工程学院，四川 成都 610031)

0 引言

压电耦合系数对于计算俘能器将机械能转化为电能具有重要影响。在压电线性本构关系中，压电耦合系数被认为是常数[1]；但也有研究结果认为压电本构关系是非线性的[2]，即压电耦合系数Θ与压电陶瓷应变X之间为二次非线性关系，即Θ=θ(1+α|X|+βX2)，其中θ为线性压电本构关系中的压电耦合常数，α和β分别为非线性压电耦合一、二次项系数。

在俘能器的性能分析中，Triplett等[3]将一次非线性压电耦合系数α≠0，β=0。结果表明，当激励较大时，非线性机电耦合关系能更准确预测俘能器输出功率。Stanton等[4]利用非线性压电本构方程推导出了压电耦合系数的二次非线性表达式，即α≠0，β≠0。Silva等[1]分别研究了压电耦合为常数、并考虑一、二次非线性耦合系数，研究结果表明：压电耦合的二次非线性能很好地与实验结果吻合，且非线性压电耦合在共振点处对俘能器输出功率影响较大。Cellular等[5]将二次非线性压电耦合系数引入到双稳态系统，证明其适用于双稳态系统，且能够提升俘能器的功率转化率。

现有对俘能器非线性压电耦合系数的研究都是以单自由度俘能器为对象展开的，且忽略了对振动位移的研究。

本文研究的L型梁俘能器是一个二自由度系统[6-7]，且振动位移能对俘能器的使用寿命有一定影响[8]。本文将二次非线性压电耦合系数引入到L型梁俘能器的性能分析中，比较不同激励幅值下非线性压电耦合系数对俘能器振动与性能的影响及其与线性压电耦合系数下俘能器振动与性能之间的差异。

1 L型梁俘能器的数学模型

图1 L型梁俘能器模型图

采用与文献[9]相同的集中参数法建立系统的计算模型。计算模型为二自由度的弹簧-质量块系统，如图2所示。

图2 集中参数模型图

根据牛顿第二定律和基尔霍夫定律，得到图2所示的L型梁压电俘能器的压电耦合控制方程：

(1)

式中：Mi为等效质量；Ki为等效刚度；Ci为等效阻尼，其中下角i=1时表示L型梁主梁参数，i=2时为副梁参数；X1为主梁相对Z的位移;X2为副梁相对主梁的相对位移；R为外接电路负载电阻;Cp为俘能器等效电容；F(X1)为磁力[11]。

对压电耦合方程无量纲化，可得系统无量纲方程：

(2)

其中无量纲参数为

(3)

(4)

X1=Lx1

(5)

X2=Lx2

(6)

t=ω1τ

(7)

(8)

V=ev

(9)

(10)

(11)

(12)

(13)

(14)

(15)

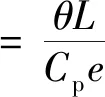
(16)

(17)

(18)

(19)

(20)

m=αL

(21)

n=βL2

(22)

式中:L为主梁长度值;MA、MB分别为两个永磁铁的磁化强度;VA、VB为永磁铁的体积；μ0为真空磁导率；d为两永磁铁之间的磁间距。

非线性压电耦合一、二次项系数α和β经过无量纲化后变为无量纲参数为m和n。

俘能器的输出功率采用无量纲均方电压表示：

(23)

式中:N为选取的结果中无量纲电压值的个数;v1为主梁的无量纲电压。

2 不同激励幅值下非线性压电耦合系数对系统响应的影响

研究表明,只有当激励幅值达到一定值时非线性压电耦合的输出功率与线性压电耦合的输出功率才会表现出明显的差异。据此，本文研究了在不同激励幅值下L型梁俘能器的非线性压电耦合系数的变化对输出功率与振动位移的影响。

采用四阶龙格-库塔法对式(2)进行数值求解，设置初始条件为0，选取无量纲参数ξ1=0.014 6，ξ2=0.012 3，μ=1.211 4，η=1.755 3，a=0.022 5，b=1.036 2，χ=0.05，λ=0.05，ϑ=0.5。

2.1 不同激励幅值下系数m对系统响应的影响

取系数n=0.5，对A0分别为0.1g(g=9.8 m/s2),1g,10g3种情况进行研究。

1)A0=0.1g时得到系统响应随m的变化如图3所示。

图3 A0=0.1 g时系统响应随m的变化

由图3可知，非线性机电耦合系数不改变系统的共振频率，且对共振点处的输出功率v2和x1的值有影响，此结论与文献[1]的结论一致。在后面的研究中为清楚地说明该参数对v2及x1的影响，仅展示俘能器在第一、二个共振点处的系统响应，分别称为共振点1和共振点2。

A0=0.1g时，L型梁俘能器在两个共振点处的x1与v2随m变化的曲线图如图4、5所示。当变参数取0值时，与线性情况下的曲线接近甚至重合。

图4 A0=0.1 g两共振点v2随m的变化

图5 A0=0.1 g共振点1中x1随m的变化

由图4可知，在俘能器的两个共振点处，压电俘能器的v2随m的增大而增大。m取负值时，小于线性压电耦合下的v2；m取正值时，大于线性压电耦合下的v2。在共振点1处，非线性压电耦合与线性压电耦合的v2的差异为-1.195%～1.195%；在共振点2处，此差异为-0.28%～0.28%。总之，当A0=0.1g时，两种耦合关系下俘能器的v2差异较小，可认为两种耦合关系下俘能器的v2相等。

由图3(b)可知，当A0=0.1g时，只在共振点1处，俘能器的x1受m的影响而产生差异，如图5所示。由图5可知，俘能器的x1随m的增大而减小。m取负值时，大于线性压电耦合下的x1；m取正值时，小于线性压电耦合下的x1。非线性压电耦合与线性压电耦合的x1之间的差异为-0.308%～0.257%。

总之，两种耦合下系统的x1差异较小，可认为x1相同。

2)A0=1g时俘能器在两个共振点处系统响应随m的变化如图6、7所示。

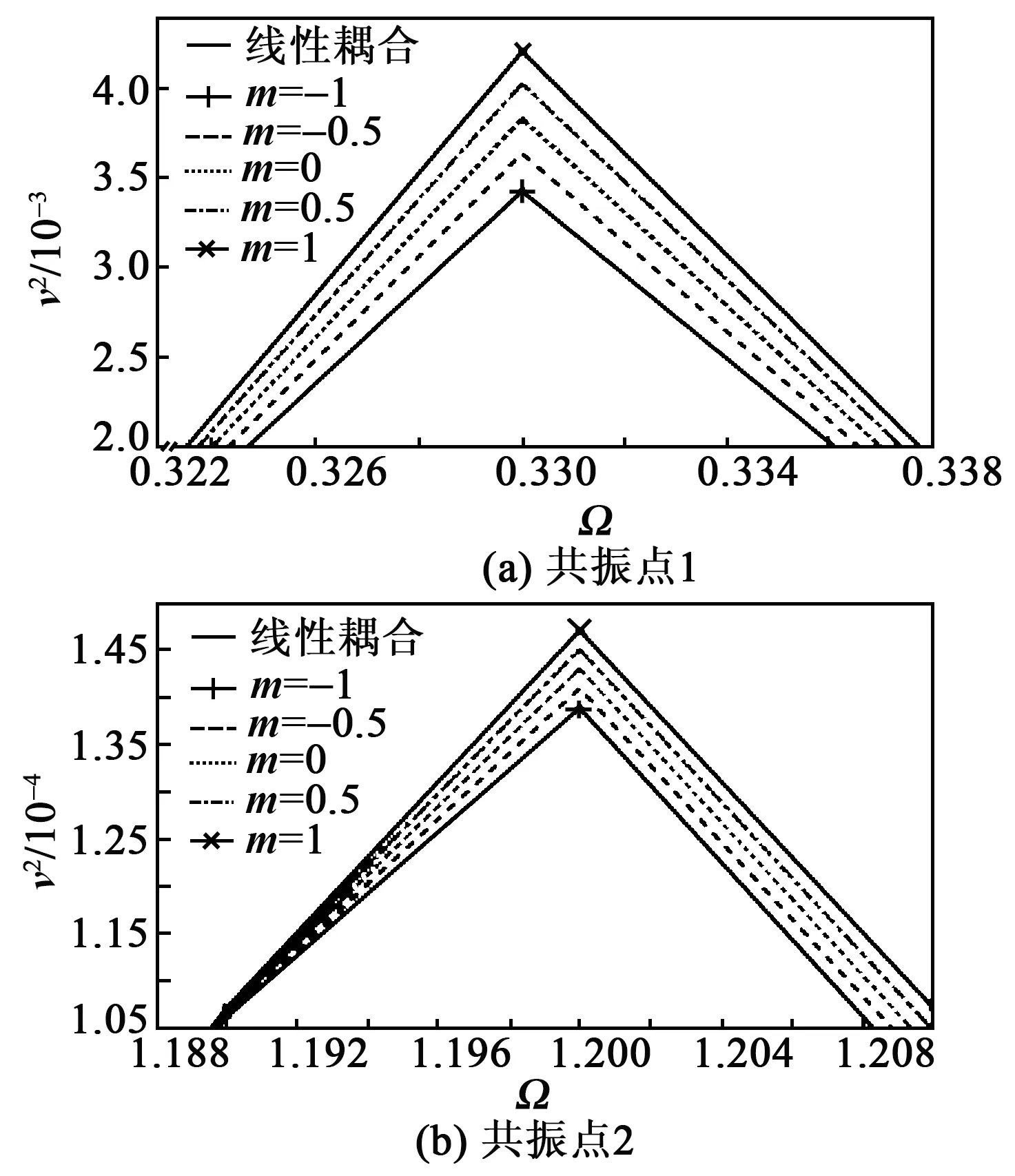
图6 A0=1 g两共振点v2随m的变化

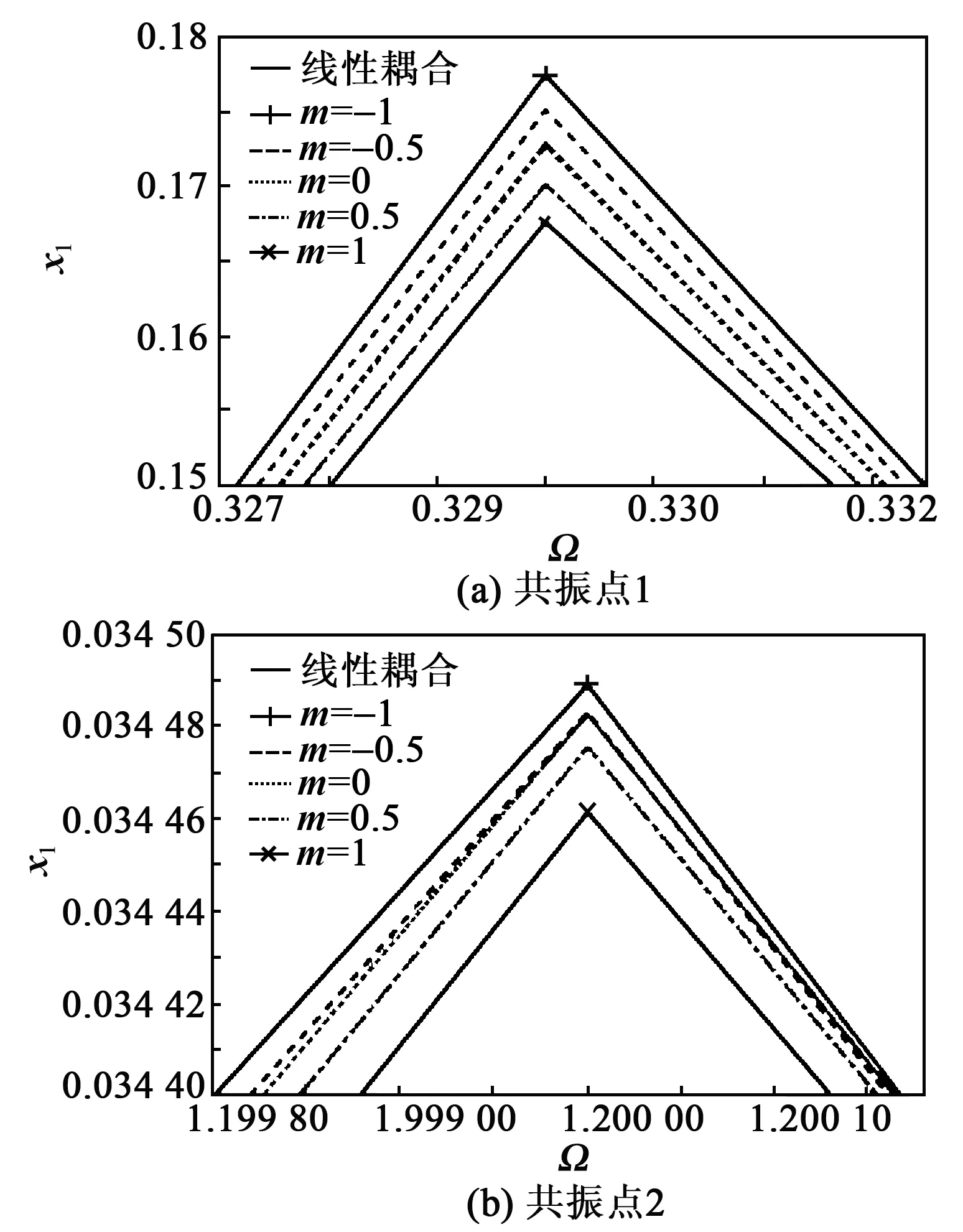
图7 A0=1 g两共振点x1随m的变化

由图6、7可知，A0=1g与A0=0.1g对应的曲线随m变化的趋势相同，只是在共振点2处，非线性压电耦合项对俘能器的x1也会受m的影响而产生差异。

非线性压电耦合与线性压电耦合下俘能器在两个共振点处的v2差异分别为-10.71%～9.59%和-2.93%～2.79%，x1的差异分别为-3.12%～2.54%和-0.058%～0.029%。

总之，在此激励幅值下，考虑非线性压电耦合项与线性压电耦合的俘能器响应在共振点1处产生了明显的区别。

3)A0=10g时俘能器在两共振点处系统响应如图8、9所示。

图8 A0=10 g两共振点v2随m的变化

图9 A0=10 g两共振点x1随m的变化

由图8可知，在此激励幅值下，两个共振点处俘能器的带宽会随m的增大而增大。

由图9(b)可知，在共振点2处，x1的幅值表现出随m的增大先减小后增大的复杂趋势，对应的共振频率呈现硬化特征。

在此激励幅值下，考虑非线性压电耦合项与线性压电耦合在两个共振点处的v2的差异分别为-48.15%～104.22%和-27.73%～21.28%，x1的差异分别为-3.14%～1.28%和0～2.5%。

总之，在此激励幅值下，两种压电耦合关系作用下的俘能器在两共振点处的响应差异明显。

2.2 不同激励幅值下系数n对系统响应的影响

取系数m=0.5，对A0分别为0.1g,1g,10g3种情况进行研究。

1)A0=0.1g时系统响应如图10、11所示。

图10 A0=0.1 g时共振点1中v2随n的变化

图11 A0=0.1 g时共振点1中x1随n的变化

在A0=0.1g下，俘能器的输出响应只在共振点1处随n变化。由图10,11可知,非线性压电耦合下俘能器的输出功率随n值增大而增大，x1随n值的增大而减小。本文研究中n的取值范围内，无论n取何值，考虑非线性压电耦合项的v2都大于线性压电耦合下的v2，x1都小于线性压电耦合下的x1。

在A0=0.1g下，考虑非线性压电耦合项与线性压电耦合在两个共振点处的v2的差异为0.585%～0.608%，x1差异为-0.154%。

总之，在A0=0.1g下，两种压电耦合下俘能器的响应差异较小，可忽略。

2)A0=1g时系统响应如图12、13所示。

图12 A0=1 g两共振点v2随n的变化

图13 A0=1 g共振点1中x1随n的变化

由图12,13可知，系统响应随n值的变化趋势与A0=0.1g时的趋势一致，不同之处是俘能器的v2在共振点2处也表现出随n值变化的特点。

在A0=1g下，考虑非线性压电耦合项与线性压电耦合在两个共振点处v2的差异分别为3.65%～5.37%和1.33%～1.39%。而x1仅在共振点2处存在差异，为-1.84%～1.04%。

总之，在A0=1g下，两种压电耦合关系俘能器的响应已存差异不可忽略。

3)A0=10g时系统响应如图14、15所示。由图14可知，在A0=10g下的两个共振点处，俘能器的工作带宽随n值增大而增大。

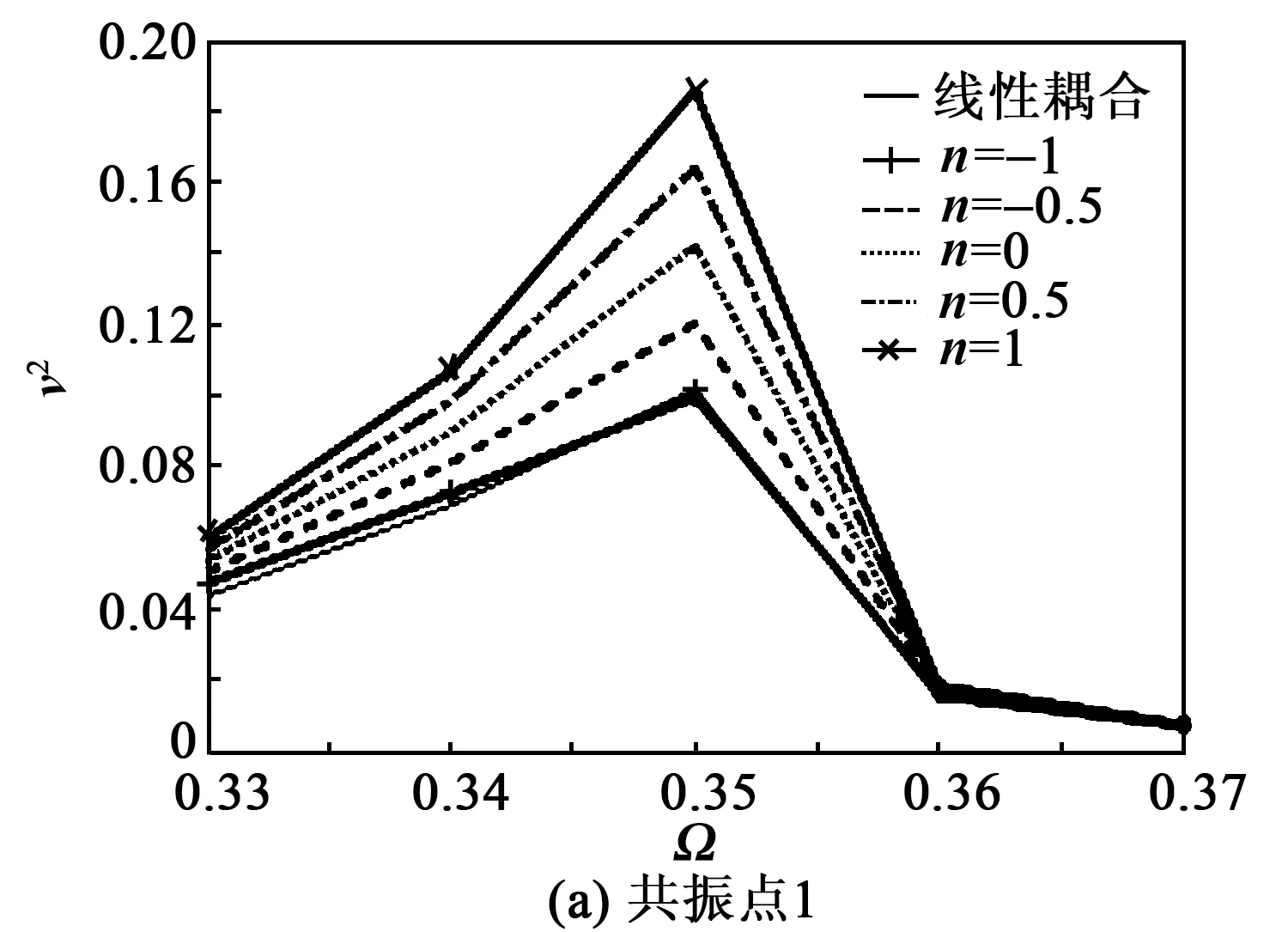
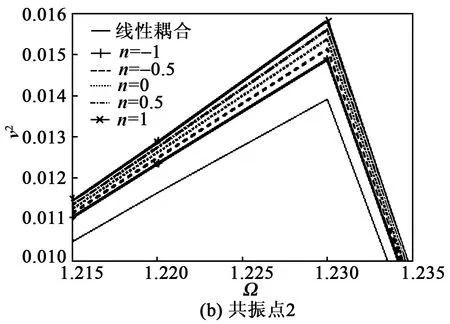
图14 A0=10 g两共振点v2随n的变化

图15 A0=10 g两共振点x1随n的变化

由图15(b)可知，在共振点2处，俘能器的共振频率也出现硬化响应的特征。

在A0=10g下，考虑非线性压电耦合项与线性压电耦合在两个共振点处的v2的差异分别为0～82.61%和6.97%～13.73%，x1的差异分别为-2.65%～0和-1.33%～2%。

总之，俘能器在共振点处两种耦合关系作用下得到的响应有较大差异。

3 结论

本文研究了非线性机电耦合对二自由度系统L型梁双稳态压电俘能器的输出功率和主梁运动的影响，主要结论如下：

1) L型梁双稳态压电俘能器在受到激励幅值较小时，非线性压电耦合项对俘能器输出功率及主梁的运动的影响较小，以线性耦合计算即可。但当激励幅值较大时，在本文研究所取参数下，激励幅值大于10g时，非线性压电耦合与线性压电耦合下的输出功率与振动位移存在明显差异。

2) 非线性压电耦合项的两个系数对俘能器输出功率及主梁的运动的影响总趋势相同。随着系数的增大，俘能器的输出功率增大，振动位移减小。这也与张宇等[10]在研究双稳态中常数压电耦合系数变化导致系统响应变化的结果一致。另外，本文的研究表明，当激励幅值为10g时，俘能器的工作带宽随这两个系数的增大而增大，并且在共振点2处出现硬化响应的特征。

3) 非线性压电耦合项的两个系数对俘能器输出功率及主梁运动的影响的区别是：m取正值时，非线性压电耦合下俘能器的输出功率才大于线性压电耦合下的输出功率，振动位移才小于线性压电耦合下的振动位移；若取负值，则相反。而n的变化使非线性压电耦合下的输出功率总是大于线性压电耦合下的输出功率，振动位移总是小于线性压电耦合下的振动位移。