基于容错决策树的UWB辅助惯性定位方法

刘 宇，陈自然，顾洪洋，付乐乐，路永乐，李星海

(1.重庆邮电大学 智能传感技术与微系统重庆市高校工程研究中心，重庆 400065；2. 中国电子科技集团公司第二十六研究所，重庆 400060)

0 引言

基于位置服务是现代生活里许多应用场景所需的关键特征，人们越来越依赖其带来的便利性。在室外，GPS、北斗等得到了很好的探索和标准化，但由于其信号易受室内复杂环境的阻隔，导致无法在室内复杂环境实现高精度的定位[1]。因此，室内高精度定位研究具有很高的商用价值。

惯性导航系统利用载体自身的角速率和加速度进行实时测量解算姿态信息和相对位置信息[2]，具有成本低,体积小,无源等优点，在短期内对室内复杂环境能有效实现较高精度定位，但惯性导航系统随着时间增长，陀螺和加速度计等惯性元器件本身产生的测量误差等使其相对定位点出现较大误差[3]，单一模式不适合长时间定位[4]。

为解决惯性导航存在的自身缺陷，在基于射频(RF)的定位技术中，超宽带(UWB)系统由于其具有高精度、低成本和低功耗，已经非常流行。与超声波相比，红外、蓝牙、ZigBee、射频识别技术和WIFI等有显著优势，虽然这些技术在一定程度上满足了部分室内活动的需求[5]，但仍存在成本高，定位精度差等缺点。目前，国内外学者提出了采用UWB定位技术的多源信息对惯性导航进行辅助修正。Lukasz Zwirello等[6]提出了一个基于仿真的紧密UWB和惯性数据集成的可行性研究；Qigao Fan等[7]提出了利用双态自适应卡尔曼滤波器的INS/UWB定位系统；曾庆化等[8]提出了基于零速修正的UWB优化配置室内行人导航。但多数学者未进行组合定位的相互容错判定，在建筑结构复杂的室内环境中，UWB定位易受到非视距问题、多径效应和人体的影响出现粗大误差，可能导致惯性导航/UWB定位精度下降，甚至错误地辅助修正惯性导航。

本文提出了一种基于容错决策树的UWB定位信息辅助修正惯性定位的方法。首先提出并采用陀螺仪高精度分段拟合误差补偿模型，抑制惯性导航误差漂移；同时将惯性导航解算的定位信息与UWB单点定位数据作为参考量共同构建容错决策树模型流程，有效剔除UWB粗大误差，进而利用2个定位结果的参数进行扩展卡尔曼滤波，实现UWB辅助增强惯性定位，实现连续性可靠定位。

1 室内惯性导航定位系统解算

本系统采用嵌入式系统作为惯性导航定位系统硬件测试平台，集成了多个惯性传感器件。该定位系统首先进行惯性导航的初始加速度计/磁力计组合姿态解算；然后对惯性器件误差校准，构建了陀螺仪高精度分段拟合误差补偿模型；根据载体自身的角速率和加速度进行实时、步数检测和步长估计测量解算姿态信息和相对位置导航信息。

1.1 初始加速度计/磁力计组合姿态解算

本文采用地理坐标系即东北天坐标系(n系)，使用加速度解算的初始俯仰角、横滚角，再加上磁力计进行共同解算，得到姿态角信息数据。设θ，γ，ψ分别为俯仰角、横滚角和航向角，且

(1)

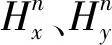
1.2 陀螺仪高精度分段拟合误差补偿

三轴陀螺仪用于采集姿态解算过程中所需要的角速度数据信息，其输出值的精确程度直接影响到姿态数据精度。为了进一步减小误差，分析了传感器自身的安装标定误差、非线性误差等，利用角速率输出误差模型，本文提出对陀螺仪进行高精度分段拟合误差补偿。角速率输出误差模型为

(2)

式中：ωx，ωy，ωz为陀螺仪真实角速率；Sx，Sz，Sy为陀螺仪标定因数；Kyx，Kzx，Kxy，Kzy，Kxz，Kyz为陀螺仪安装误差系数；Bx，By，Bz为陀螺仪零偏；wx，wy，wz为陀螺仪实际角速率测量值。

在高精度分段拟合误差补偿的实验中，选取三轴转台动态速率为-100～100 (°)/s，以10 (°)/s作为间隔，共20个角速率，每组采集保留500 kbytes数据。按照速率数据正负对称和动态速率高低，将20个角速率分为8组，在每个分段组中，以取三轴转台动态速率值为横坐标，陀螺仪真实角速率为纵坐标，对其数据进行拟合，得到各轴该分段组标定因数Sx、Sz、Sy，安装误差Kyx、Kzx、Kxy、Kzy、Kxz、Kyz及零偏Bx、By、Bz。

以x轴为例,设置动态速率为-100 ～100 (°)/s，对x轴原始误差和校准后误差进行均值记录(见表1)。

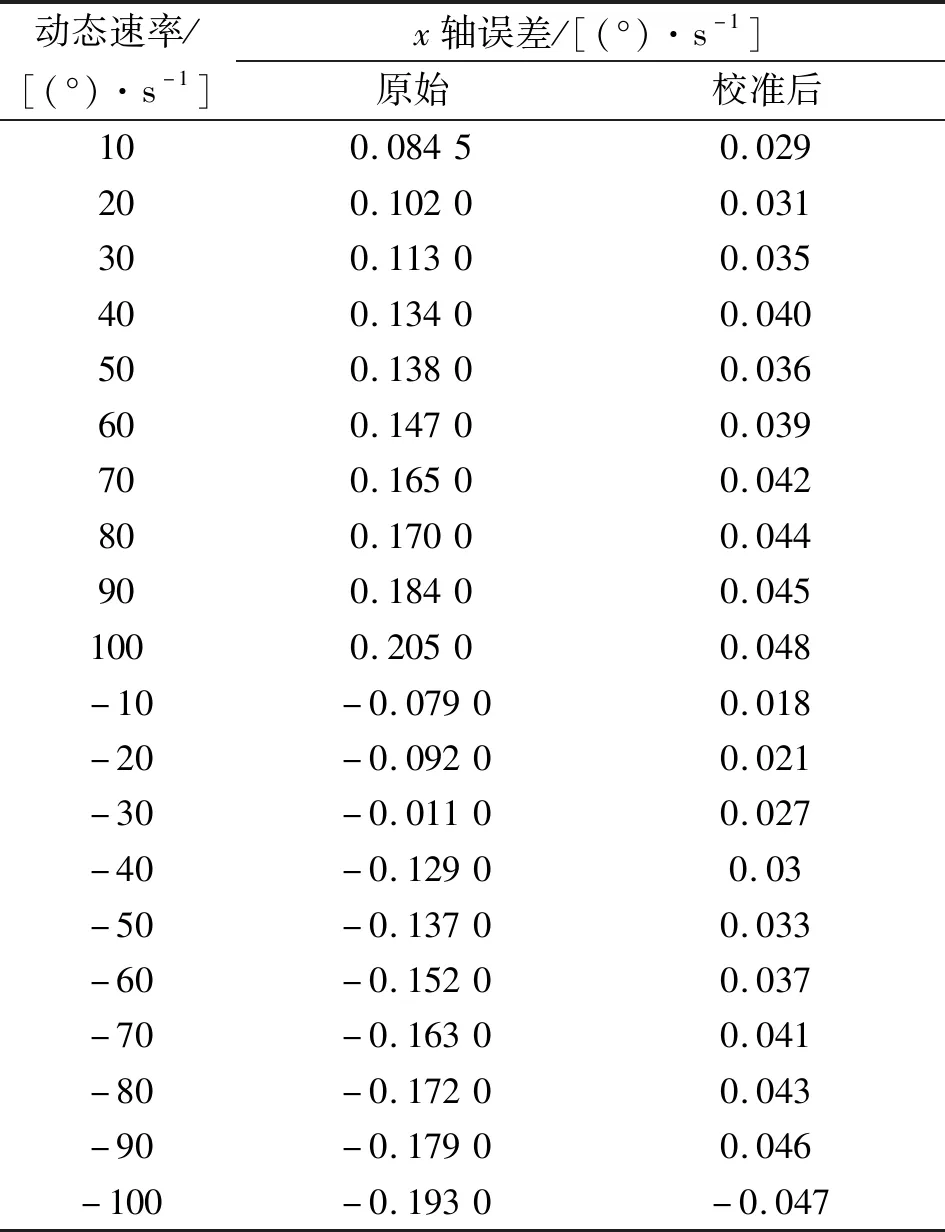
表1 陀螺仪高精度分段拟合误差补偿前、后对比表

由表1可知，经过高精度分段拟合误差补偿后，可区分补偿高低动态速率段，更进一步消除角速率输出误差，减少了1～2个数量级。

1.3 四元数姿态解算

采用四元数算法对传感器测量值进行姿态解算，利用惯性导航姿态解算的四元数参考值，实时计算出坐标矩阵，结合姿态转换算法，即可解算出i时刻三轴θ、γ、ψ分别为

(3)

式中：q0为四元数的标量；q1、q2、q3为四元数的矢量。

1.4 步数检测和步长估计

根据加速度特征数据仿真发现，行人走路的波峰、零点和波谷数据有似正弦波的周期性规律，利用汉明窗提取特征数据。但由于行走过程中身体存在抖动，加速度波形可能出现伪波峰，进一步消除其造成的步数误判采用阈值判别法：

(4)

阈值范围内，检测到一个有效步数是以有效波峰值和有效波谷值为周期。经实验验证，人员行走108步，则检测到的有效波峰为108个(见图1)，此方法能准确检测人员行走的步数。

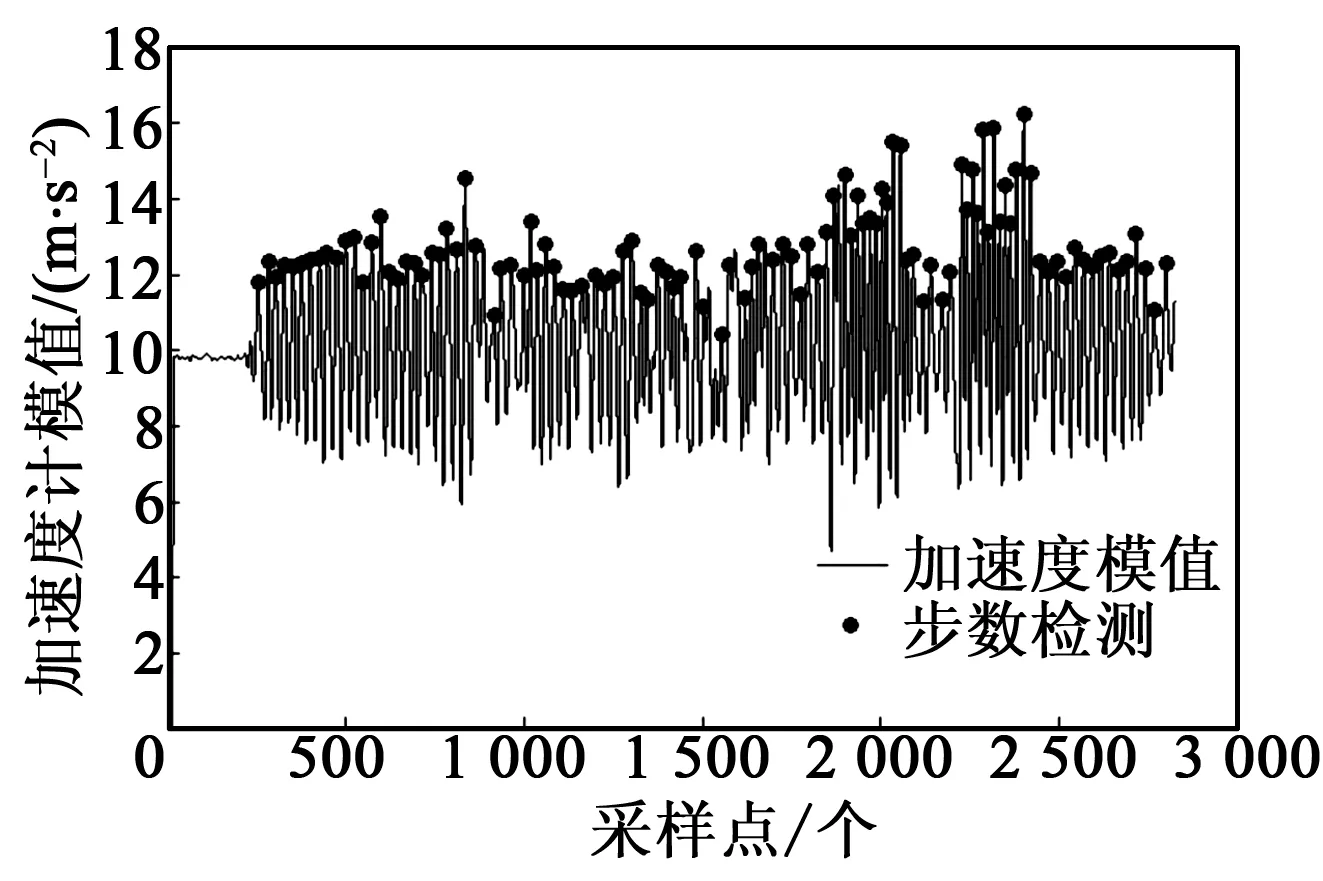
图1 加速度步数检测图

利用加速度与人员行走时刻步长的波峰、波谷差值之间的关联性，采用下式进行自适应步长计算：

(5)

式中：j为行人的第j步；Lj为行人第j步的实时步长；K为行人步长标定参考值；amax,j、amin,j分别为第j步目标加速度最大波峰值、最小波谷值。

2 UWB定位系统解算

UWB定位是一种基于距离测量的室内高精度定位通信新技术，一定范围内准确获得人或物的位置和导航信息。本文的UWB定位测距通信模块使用双向飞行时间(TW-TOF)测量2个以上UWB模块的间距，其可提供具有短脉冲的精确时间测量，同时保持对多径信号传播的鲁棒性。

TW-TOF不要求通信双方时间的同步性，自模块运作后将拥有其独立的时间戳,如图2所示。

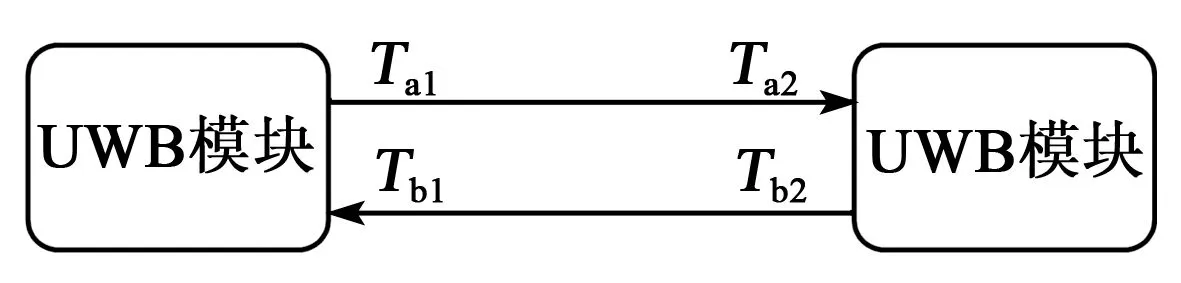
图2 TW-TOF测距方法

首先分别得到模块A、B的脉冲发送和接收时刻的传递时间Ta、Tb为

(6)

再利用无线电信号传播的速度即光速c，可计算2个实体的距离p为

(7)

3 基于容错决策树的UWB辅助惯性定位

惯性导航系统对载体自身的角速率和加速度进行实时测量，解算得到姿态信息和相对位置导航信息后，利用UWB定位辅助增强室内定位精度，实现多传感器多源定位信息下的连续性可靠定位。UWB设备的布设将针对不同的室内环境而定，在复杂狭窄巷道环境时，两端布设UWB基站进行辅助；常规环境下，在同一楼层拐点或分叉口布设UWB基站进行辅助，合理减少室内环境中UWB基站数量。UWB所获得的定位数据用于辅助修正惯性导航解算的定位信息，降低系统随时间累积误差。

3.1 UWB单点定位数据的容错决策树判定

在室内环境中，由于UWB定位存在易受遮挡物引起的非视距(NLOS)误差及信号不稳定等多种影响定位精度情况，先行对UWB是否接收到多边基站信号和出现粗大误差进行有效判定，并将惯性导航解算的定位数据作为决策树容错判定的参考量共同构建模型流程。

在容错判定开始前将当前k时刻的UWB单点定位数据作为输入量。

首先进去到第一层容错判定，需要获知UWB标签是否接收到定位基站的脉冲信号，则利用Tuwb标志位判定是否存在UWB单点定位数据,即

(8)

通过Tuwb标志位判定后，利用UWB单点定位数据获得其标签与定位基站之间的飞行时间后，使用TW-TOF测量标签与各基站的定位距离，由式(7)可解算得距离p。

在通过TW-TOF法获得标签到多个定位基站的距离后，本文选用三边测距定位法计算行人当前k时刻的移动位置最优解Puwb,k(xn,yn)：

(9)

式中:xn,yn分别为由n个UWB定位基站共同解算的标签x、y轴移动位置最优解;pn为标签到第n个定位基站的距离。

UWB定位基站的布设数量根据不同的室内环境而定，若行人处于复杂狭窄巷道环境中，行人将UWB标签与惯性定位模块集成一同放在腰间，可能出现无法接收3个及以上的基站时间戳的情况，则默认由TW-TOF得到的2个基站距离p1、p2计算位置信息；若行人处于常规方正室内环境，在房间4个拐点UWB基站进行辅助，则默认由TW-TOF得到的多个基站距离p1、p2、p3、p4计算二维位置信息。

通过第一层容错判定，若不存在UWB单点定位数据，单边基站所得到定位数据不具可信度，则不使用UWB辅助惯性导航解算。如果存在UWB单点定位数据，由于UWB数据存在粗大误差在第一层容错判定中无法完全消除，需结合惯性导航定位数据作为参考量,进一步提高可信度。

接下来进入第二层容错判定，在复杂狭窄巷道环境时，根据行人运动规律特性，安放在人员腰间的定位模块出现航向角度大幅变化时，UWB数据存在粗大误差的几率降低。故在此环境下，需要利用当前k时刻惯导解算对应的航向角ψk和初始航向角ψzero进行判断行人是否发生转弯模式变化。

(10)

式中：Δψ为k时刻航向角与初始航向角的差值绝对值；ε为判断行人转弯模式的活动阈值。

从第二层容错判定中可看出，行人转弯模式是对UWB粗大误差的剔除，在确定转弯判定能接收到基本精确的UWB单点定位数据后，需结合惯性导航解算的位置数据和行人步数进行判断位置条件，进入第三层容错判定。若不在复杂狭窄巷道环境下，直接进入第三层容错判定。

根据在行走定位过程中的运动特性，佩戴人员在常规情况下，其前、后采样点的位置不会突变，应该满足UWB位置和惯性导航位置之间的距离差条件。并且随着运动时间累积，其距离差值将会保持在合理范围内。因此，采用同一采样点的惯性导航与UWB定位信息差Δp进行测量数据的活动阈值判定，即

(11)

式中：Pins,k为惯性导航在k时刻的位置数据；Puwb,k为UWB在k时刻单点定位距离数据；σ为惯性导航与UWB位置数据之差的活动阈值。

考虑到随时间累积后定位误差的线性变化，若UWB和惯性导航解算位置差保持在合理的范围内，允许其σ存在波动。由于在时域中无法将每一时刻与距离误差一一对应，故使用行人运动步数与距离间的关系，其σ能同时满足下列行走步数范围的关系为

(12)

式中：step为加速度解算的有效步数；σ1，σ2，σ3为分段步数对应的阈值。

经过容错决策树的三层判定，最终实现了利用惯性导航解算的定位信息与UWB单点定位数据作为参考量，共同构建容错决策树模型流程，提高了定位精度。

3.2 基于扩展卡尔曼(EKF)滤波的惯性导航/UWB定位信息融合

通过UWB单点定位数据决策树容错判定后得到了当前时刻稳定的位置信息，将其作为观测信息与惯性导航解算数据进行滤波，其状态方程与观测方程如下：

(13)

式中：k为离散时间所对应的时刻，系统在k时刻的状态Xk∈Rn；Zk∈Rm为对应状态的观测信号；Φk为状态转移矩阵；Gk为状态噪声驱动矩阵;Wk∈Rn为输入信号的白噪声;φk为非随机的外作用项;Hk为观测矩阵;Vk∈Rm为观测信号的白噪声。

设计X=[δp,δv,δφ,δa]T为该EKF滤波的状态向量，包含12个状态量，其中行人的位置误差δp(δpx、δpy、δpz)、惯性导航东、北、天坐标的速度误差δv(δvE、δvN、δvU)、当前时刻惯性导航所解算的姿态角误差δφ(δφγ、δφθ、δφψ)以及三轴加速度误差δa(δax、δay、δaz)作为状态向量，E、N、U分别为东、北、天坐标系中的东向、北向和天向位置。

针对姿态角误差补偿，当初始时刻检测到开机站立时，默认此时惯性导航解算的姿态角为初始姿态角。将惯性导航解算的实际姿态角与初始姿态角之差Δψ作为当前时刻姿态角的观测量。针对位置误差补偿，使用惯性导航与UWB解算的位置信息之差作为当前时刻位置的观测量Δp。观测向量Z=[Δp,Δψ]。其中：

(14)

式中wΔp，wΔψ为对应观测量的观测模型噪声。在这个过程中，假设wΔp，wΔψ相互独立且满足高斯白噪声。首先对状态方程进行求导可得Φk为12×12的状态转移矩阵，即

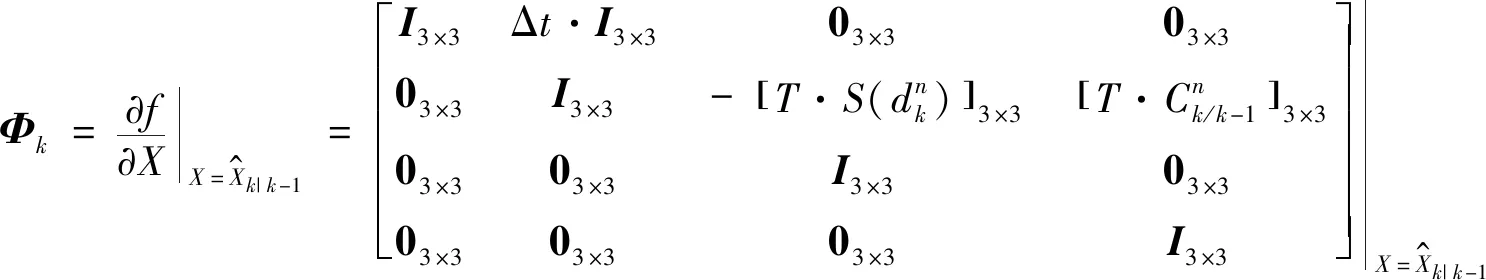
(15)

Hk为观测量的转换矩阵，且

(16)

4 实验验证与分析

为了验证本文提出的基于容错决策树的UWB辅助惯性导航解算可靠性，将UWB标签与惯性定位模块集成，佩戴在行人后背的腰间(见图3)，以便在行走过程获得更稳定的位置数据。实验中惯性定位采用集成了三轴陀螺仪、三轴加速度计、三轴磁力计等传感器的嵌入式微系统作为硬件平台，通过传感器数据实时解算行人的位置和航向；UWB使用定位测距通信模块，定位基站的布设根据不同的室内环境而定。定位系统的上位机实时接收惯性导航和容错判定后的UWB解算定位数据，再利用EKF滤波对定位信息融合。

图3 惯性定位模块和UWB装置

本文分别在两种不同环境下进行实验，以证明基于容错决策树的UWB辅助人员室内定位在复杂和常规环境均有效。第一种实验在复杂狭窄巷道环境中，验证能否准确进入到对应的房间；第二种实验在常规方正室内环境，轨迹类似于矩形，验证系统的可靠性。由于UWB信号通常无法穿过建筑物的混凝土墙，这导致大量的信号延迟，故本实验不考虑高度问题，在2D平面进行定位。

4.1 复杂狭窄巷道环境

设定实验环境在重庆邮电大学第一教学楼(见图4)，激光测距可得其直线过道长为33.23 m。该过道配备有2个UWB接入点，分别置于左、右两端AP1(0,0)、AP2(0,33.23)，在图中用▲表示。为了更好地对比纯惯性导航解算和UWB辅助的定位系统精度，选取5个教学房间，规定统一的行走路线：起点AP1→房间①→房间②→房间③→房间④→房间⑤。行人出发航向由初始加速度计/磁力计组合姿态解算ψzero，二维坐标为(0,0)，并规定行人结束时方向与出发时一致。

图4 第一教学楼建筑结构图及行走路线

图5(a)为行人在过道及进入教学房间过程中，纯惯性导航和惯性导航/UWB辅助定位的上位机行走界面。图5(b)为实验效果对比仿真图。

图5 上位机实际行走及实验效果对比仿真图

图5中行走路线的理论起点、终点分别为AP1(0,0)、AP2(0,33.23)，通过实验对比分析，复杂狭窄巷道环境下，在无UWB辅助的纯惯性导航时，位置和航向角逐渐偏离真实定位轨迹，且随着时间的增长，其相对定位点出现较大误差，呈现连续变化特性。

由图5(b)可看出，当行人进入到房间时，有效的UWB测量单点定位信息辅助修正惯性导航，将行走轨迹拉回到正确的区域，无UWB辅助修正的惯性导航定位无法解算原始轨迹现。当行人到达理论终点AP2时，纯惯性导航解算点为A(6.2，36.56)，惯性导航/UWB定位解算点为B(0.39，34.03)，实际行走距离长度为116.86 m。根据数据计算可得，A点到起点的均方位置差为7.038 m，距离均方误差占路线长度的6.02%；B点到起点的均方位置差为0.89 m，距离均方误差占路线长度的0.76%。

4.2 常规方正室内环境

设定实验环境在重庆邮电大学第七教学楼,室内配备4个UWB定位基站(见图6)，均安装在房间的拐角处天花板墙上。UWB定位基站坐标由激光测距仪得到，分别为AP1(0,0)、AP2(0,39.5)、AP3(18.5,39.5)、AP4(18.5,0)，在图中用▲表示。实验统一的行走路线为从起点AP1沿逆时针方向，分别经过AP2、AP3、AP4，绕行两圈回到起点AP1。行人出发航向由初始加速度计/磁力计组合姿态解算ψzero，并规定行人结束时方向与出发时一致。

图6 第七教学楼建筑结构图及行走路线

图7为行走路线的纯惯性导航和惯性导航/UWB辅助定位的实验效果对比仿真图。由图可以看出，纯惯性导航定位路线随着时间累积误差，在第二圈时出现了较大的位置漂移；惯性导航/UWB定位路线有效剔除了UWB粗大误差定位信息，并快速辅助修正惯性导航长时间连续定位的误差，与实验规划路线吻合较好。当行人绕行两圈回到AP1时，纯惯性导航解算点为A(0.542，1.294)，惯性导航/UWB定位解算点为B(-0.124，-0.061)，实际行走距离为232 m。由于实际行走轨迹为常规方正矩形，存在各个方向漂移相互抵消，故不只限于分析终点误差值。纯惯性导航的距离误差为-1.38～5.12 m，最大误差占路线长度的2.207%；惯性导航/UWB定位的距离误差范围为-1.473 8～0.160 3 m，最大误差占路线长度的0.635%。

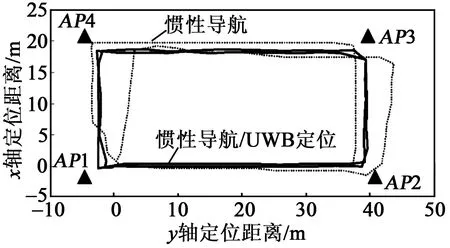
图7 实验效果对比仿真图

综上所述可知，与纯惯性导航相比，在复杂狭窄巷道和常规方正室内环境下，惯性导航/UWB定位系统人员行走真实路径与规划路径更贴合，显著降低了定位误差，有效抑制误差随时间累积漂移，实现了多传感器多源定位信息下的连续性可靠定位。

5 结束语

本文针对惯性导航系统误差随时间累积和UWB定位受到非视距问题、多径效应和人体影响出现粗大误差的问题，提出了一种基于容错决策树的UWB辅助惯性定位方法。该方法采用陀螺仪高精度分段拟合误差补偿模型，抑制惯性导航误差漂移；同时构建UWB单点定位数据的容错决策树判定，剔除粗大误差因子，进而使用惯性导航和UWB参数进行扩展卡尔曼滤波，实现UWB辅助增强惯性导航定位。

实验中惯性定位采用集成了三轴陀螺仪、三轴加速度计、三轴磁力计等传感器的嵌入式微系统作为硬件平台；UWB使用定位测距通信模块，定位基站的布设根据不同的室内环境而定。根据实验平台对两种不同环境进行实验验证。在复杂狭窄巷道环境，本算法将距离均方误差占路线长度的比例从6.02%提升到0.76%；在常规方正室内环境，本算法将最大误差占路线长度的比例从2.207%提升到0.635%。实现了长时间的连续可靠定位，具有很强的工程应用价值。